1. SUBMIT TO: E105
2. SUBMIT EACH ABSTRACT TO ONE CONFERENCE ONLY.
Practical Holography XV
Stephen A. Benton
3. ABSTRACT TITLE: Nonparaxial Talbot effect.
AUTOR LISTING:
Valeriy S. Feshchenko, Benderskogo vosstanja
str. No 3, flat 22, Benderi 278100, Moldova, feshchenko@mail.ru
Alexander N. Malov, Baikalskaja str., No
196, flat 35, Irkutsk-31, 664031, Russia, malov@physdep.isu.ru
Olesya A. Rogodjnikova, Karla Libknekhta
str. No 205/3, flat 17, Tiraspol, 3300, Moldova
Yury N. Vigovsky, Novoslobodskaja str. No
31/1, Moscow, 103055, Russia, vigovsky@dol.ru
5. PRESENTATION: Poster Presentation
6. ABSTRACT TEXT:
One of important applied directions in diffraction
physics is optical data processing, that in general kind is
fulfillment of operations with multidimensional signals. Airborne
reconnaissance data, x-ray photographs, radar images and etc.
is multidimensional signals.
In present article the phenomenon of a self-imaging
of the images of periodic object (Talbot effect) in nonparaxial
area of a diffraction is experimentally investigated. Transformations
of periodic fields of an optical range for optical processing
of the two-dimensional images are offered and investigated.
Is shown, that a choice of various geometry of the optical
scheme for synthesis of the images of periodic object in the
nonzero diffraction orders, permits to execute transformation
the two-dimensional image in one-dimensional and back - one-dimensional
to two-dimensional image.
Method of formation of images of the periodic
objects in nonzero diffraction orders is offered and investigated,
which can are used the basis for systems of images multiplication.
7. KEY WORDS: Array , nondestructive testing, optical signal
processing, Talbot effect.
8. BRIFF BIOGRAPHY: Valeriy S. Feshchenko
received the MSc degree in physics from Moldavian State University
in 1991 and the DSc in radiophysics from the Irkutsk State
University, Russia, 1998. He work as senior scientist at the
laboratory of Coherent Optic and Holography in Dniester State
University, 25 October str. 128, Tiraspol, Moldavia. His research
interest include holography, optical data processing, nondestructive
testing and laser light interaction with biotissue.
Nonparaxial Talbot effect.
Valeriy S. Feshchenko1, Aleksander N. Malov2,
Olesya A. Rogozhnikova1,
Yury N. Vigovsky3
1Dniestr State University, 25 October str,
128, Tiraspol, Moldavia, feshchenko@mail.ru.
2Irkutsk State University, Gagarin str, 20,
Irkutsk, Russia, malov@physdep.isu.ru
3MeDia Co, Novoslobodskaja str. No 31/1, Moscow,
Russia, vigovsky@dol.ru.
Abstract
The phenomenon of a self-imaging of the images
of periodic object (Talbot effect) in nonparaxial area of
a diffraction is experimentally investigated. Method of formation
of images of the periodic objects in nonzero diffraction orders
is offered and investigated, which can are used the basis
for systems of images multiplication.
Keywords: optical image processing, periodical
objects, Talbot effect.
- Introduction
One
of important applied directions in diffraction physics is
optical processing of information files, that in general
way assumes fulfillment of operations with multidimensional
signals which are functions of several variables. As multidimensional
signals it is possible to consider airborne reconnaissance
data, x-ray photographs, radar images and etc.
The
given article shows, that the structure of the arising self-images
is connected with the presence of local cross nonuniformities
of a field within the limits of one space period of structure,
and with unlocalized influence on field of all aperture
of a subject or optical system. The self-imaging phenomenon
of periodic object images (Talbot effect) in essentially
nonparaxial area of diffraction is experimentally investigated.
Periodic fields transformations of an optical range for
optical processing of the two-dimensional images are offered
and investigated too. Is shown, that a choice of various
of geometry of optical schemes for synthesis of periodic
subject images in nonzero diffraction orders permits to
execute transformation of the two-dimensional image into
one-dimensional and on the contrary.
The
method of formation of periodic objects images in nonzero
diffraction orders is offered and investigated, which can
form the basis for systems multiplication of the images.
- Main
theory.
- Diffraction
of light on periodic object.
Let
the transmission of the individual image will be te
(x, y), then the transmission of a rectangular object
in the way of a matrix from MxN of individual elements fig.1
can be presented such as follows:
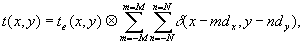
(1)
where
M and N - integers, dx - period of a matrix along
axis x, dy - period of a matrix along axis y,
Ä - operation of convolution, d - Dirac delta-function.
It
is known, that the peak distribution appropriate to this
transmission will be observed on so-called Talbot distance
[1]:
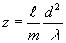 ,
,
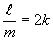 ,
k=1, 2,..., (2)
,
k=1, 2,..., (2)
where
l and m - mutually simple numbers, l - wavelength
of radiation, d-period of a object.
The
distribution of amplitude in Talbot’s plane will be:
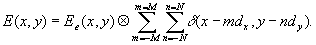 (3)
(3)
Thus
the periodic object may be to presented as a superposition
of a diffraction grating and mosaic image made from individual
elements.
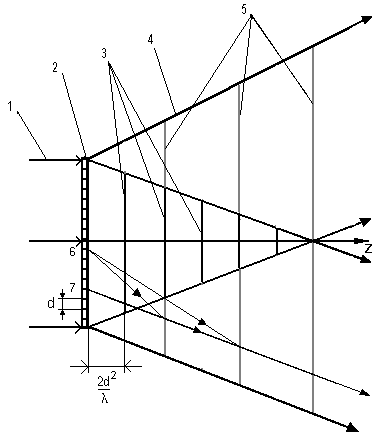
Fig.1.
Scheme of distribution of electromagnetic radiation behind
periodic object. 1-incident electromagnetic wave, 2-periodic
object, 3-paraxial Talbot’s planes, 4 - diffracted beams,
5- nonparaxial Talbot’s planes, 6,7 - various cells of periodic
object.
The
property of diffraction gratings is known to multiply the
image of periodic object in both parties from optical axis
(fig.1). In this case in Talbot plane, in nonzero diffraction
orders, following distribution the amplitudes is formed:
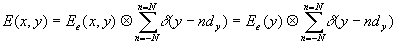 ,
(4)
,
(4)
for
diffraction orders multiplied along axis X, and
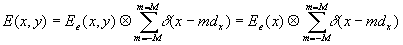 ,
(5)
,
(5)
for
diffraction orders multiplied along axis Y.
Because
of filtering property d - function in nonzero diffraction
orders there will be the subtraction of those elements of
object, which are not perpendicular axes, along which there
is the multiplication. Two-dimensional object will become
one-dimensional object.
In
fig.1 this process is submitted in the way of the scheme.
In paraxial areas, where all diffracting light beams are
crossed, classical Talbot effect is observed, i.e. the Talbot
planes, designated in fig.1 with the point 3, placed along
axis on distances satisfying to a condition (2). There is
space area, where the diffraction orders with different
signs are not crossed. To this area ratio (4) and (5) correspond.
In these space areas the self-image occurs owing to coincidence
phases of wave fronts from identical elements of different
(points 6 and 7 in fig.1) individual images. As outside
of axis there is a overlapping only nonzero orders of one
sign, and the image will be formed only by the nonzero diffraction
orders.
We
shall find out now, on which distance between them the self-image
planes in nonzero diffraction orders will place.
It
is known, that the distance between self-image planes in
axial Talbot effect is defined by that change of a wave
front phase, at passing by them of this distance in free
space, should be divisible 2p . Distance between self-image
planes in nonzero diffraction orders will depend on this
factor too.
We
shall consider, that a phase of the image in nonzero diffraction
orders from images phase in zero order differs. If we present
amplitude of an optical field at periodic object [2] near
to axis of a incident radiation beam in the following way:
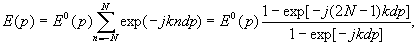 (6)
(6)
where
k=2p /l , dp=d (sinq -sinq 0)
- complete difference of a course between light ray, come
in a remote point of supervision from appropriate points
of two next individual images, where
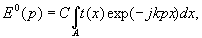
distribution
of amplitudes from individual image. The phase of this image
in this case will be j = (2N-1) kdp.
For
that of a object on edge of a beam the condition (6) can
be written in way:
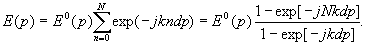 (7)
(7)
The
phase of image in this case will be j 1
= Nkdp. At N® ¥
, j /j 1®
2.
Thus,
if the phase of image in zero order will satisfy to a condition:
j
=2p n, where n=1,3,5... N.
(8)
The
image in zero order will have positive contrast, and in
the field of geometrical shadow and nonzero diffraction
orders - negative contrast.
In
case if the phase of image in zero order will satisfy to
a condition::
j
=2p n, where n=2,4,6... 2N.
(9)
And
in zero diffraction orders and in nonzero diffraction orders
there will be the positive contrast.
Thus,
distance between planes of self-image in nonzero diffraction
orders along axis z, will be in two times more, than distance
between paraxial self-image planes.
In
planes of observing not coincident with the plane of periodic
object, spectrum of field of object is principle finite.
This occurs in consequence of divergences in the space of
high harmonics of limited bunches, as well as in consequence
of the wave nature of light, thanks to influence of quickly
damped waves. As a result images located in nonparaxial
area will be subjected to distortion. Known [66], that in
the spectrum of limited subject in paraxial area when moving
from image centre to edge in Talbot's planes total quantity
of overlapped harmonics does not decrease. Number of symmetric
overlapped harmonics decreases only, thanks to that the
quality of images is deteriorated. When diffraction of radiation
into nonparaxial area is occuring, the image is primordially
formed by the orders of diffraction of one sign and the
threshold frequency which according to [4] equal to
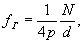 (10)
(10)
where
p- real number, N - quantity of elementary cells in object,
d - the period of a object, is achieved on edge of a paraxial
zone. And further there is only the decrease of general
number of space harmonics in image. Therefore the best images
is located on edge of a paraxial zone. The deterioration
of images quality at the expense of separation of nonzero
harmonics can be described, as well as in paraxial case
[4] by Linfoot's quality factor:
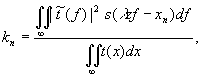 (11)
(11)
where
~ - mark of Fourier transformation of function, f -
spatial frequency, s - coherent transmission function of
a periodic object as of optical system, l - wavelength,
xn - coordinate of the elementary image, t(x)
- function of transmission of the elementary image. The
counting of coordinate xn it is necessary to begin from
edge of a paraxial zone but not from center of the image,
as in paraxial case, and as t(x) is necessary to select
an one-dimensional component of transmission function of
the elementary image.
Thus,
the shaping the self-imaging on the mechanism of Talbot’s
effect corresponds to a modified principle E. Abbe about
double diffraction in the time of formation of the image
[5]. According to him, when imaging possible to select diffraction
on elementary components of object and diffraction on totality
of components located periodically on the field of subject.
Hereupon delay of phase of various components of angular
spectrum which required for imaging occurs because of what
a radiation that is diffracted on identical elements of
various elementary images make a various way in the free
space. Since both types of a diffraction occur in one plane,
it is possible to form the images in nonzero diffraction
orders of radiation on periodic subject, and not just along
optical axis.
- Experimental
research of light diffraction process on periodic object.
3.1. Scheme of transformation of a two-dimensional
image of object in one-dimensional.
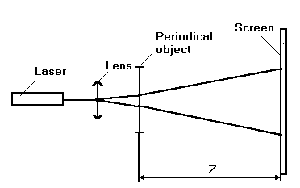
The scheme (see fig.2) consist of helium-neon
laser, a lens, periodic object and screen. The object is demonstrated
on fig. 3, was produced by a method hardening bleaching on
photographic film "Mikrat-izopan"(Slavich, Russia) on technique,
described in [6]. The periodic object was purely phase. The
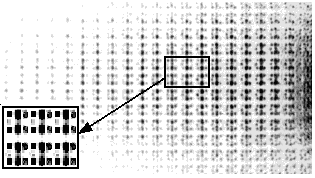
example of subtraction is submitted on fig. 4.
As it is visible on photo, in nonzero diffraction
orders the elements, which are not perpendicular axes, along
which there is the multiplication will be lacking.
Fig.5 explains, which just the elements were
suppressed in these images. The spatial filtering occur at
the expense of three-dimensional geometry of the scheme, instead
of two-dimensional geometry as in classical schemes of matched
spatial filtering. The special holographic matched Vanderlugt
filter [5] is not required in this case. Therefore and the
accuracy of such processing is not limited, for example, properties
of the holographic filter and its noise.
Using same optical scheme the change dependence
of the phase of image which formed in nonzero diffraction
orders from change of phase of image in paraxial area was
investigated.
 |
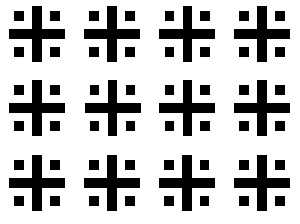 |
| Fig.2. Optical scheme for observation of Talbot’s effect.
Z – Talbot’s distance. |
Fig.3. Periodic object. |
|
|
|
Fig.4a. Multiplication along axis X.
|
Fig.4b. Multiplication along axis Y.
|
|
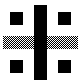
|
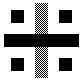
|
|
Fig.5a. The elementary image of a of
a periodic object with fig.3. The parts of the elementary
image are shaded which were subtract at multiplication
along axis X.
|
Fig.5b. The elementary image of a of
a periodic object with fig.3. The parts of the elementary
image are shaded which were subtract at multiplication
along axis Y.
|
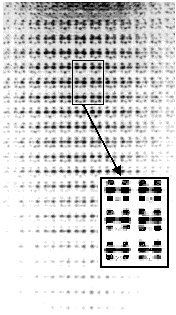
On photos presented on fig.6a Talbot's plane
the phase of image in which satisfy to a condition (8) is
demonstrated. It is visible, that dark points in paraxial
image (noted on fig.6a by a square) is corresponded bright
points in image generated in the nonzero orders (on fig.6a
is noted by a rectangular). In other words the image in nonzero
diffraction orders is inverted concerning image in paraxial
area. It means, that the phase of image in nonzero diffraction
orders is shifted relatively of the phase of image in paraxial
area in odd number p .
And on fig.6b. the image in other Talbot's
plane is demonstrated and the phase of image in this plane
is satisfied to a condition (9). It is visible, as in nonzero
diffraction orders (is noted on fig.6b by a rectangular) and
in paraxial area the central points of the images remain dark.
It means, that the phase of image in nonzero diffraction orders
is shifted in relation to phase of image in paraxial area
in even number p .
|

|

|
|
Fig.6a. The image of a periodic object
in Talbot’s plane. The image phase in nonzero diffraction
orders is displaced on p
.
|
Fig.6b The image of a periodic object
in Talbot’s plane. The image phase in nonzero diffraction
orders is displaced on 2p
.
|
Thus, there is the opportunity in same plane
to obtain the multiplied positive and negative images
If the matrix consists of individual elements
having a way shown on fig.7. multiplcation occurs in a direction
perpendicular toward side of triangle In this case we also
are using scheme (fig.2) but then it is possible to obtain
only three groups of the multiplied images and not four. Quantity
of axes along which images are multiplied equally to quantity
of axes of symmetry, as is demonstrated on fig.8a.
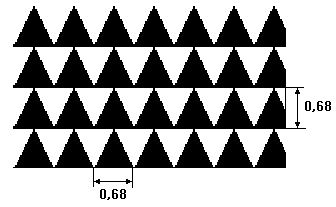
Fig.7. Periodical object, which three axes
of symmetry has.
On fig.8b the paraxial image of a object
in Talbot's plane is demonstrated. According to theoretical
accounts [7] in this case we must observe amplitude distribution
in the form of dark triangles and bright places between them.
But in fact we see in the image only contours of the elementary
objects. This fact is possible to explain by that a object
is transparent (phase) and in place where the phase of a wave
varies the poorly essential contribution to image add the
light which pass through periodic object without a diffraction.
It is in other words possible to say that the small variations
of an intensity are overlaped by high coherent noise.
|
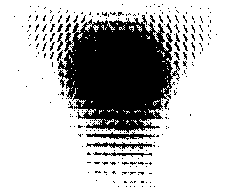
|

|
|
Fig.8a.
|
Fig.8b.
|
3.2. Synthesis of the images in nonzero diffraction
orders.
In previous paragraph the mechanism of formation
of the Talbot images in nonzero diffraction orders was considered.
Taking into account this mechanism it is possible to offer
set of interesting practical applications for effects which
arise on the diffraction of light in area where nonzero the
orders of a various sign are not overlaped.
So, for example, it is possible to synthesize
the image of periodic object in nonzero diffraction orders.
If the image with distribution of amplitudes as in (4) is
superimposed on another image with distribution of amplitudes
as in (5) in Talbot's plane we shall obtain:
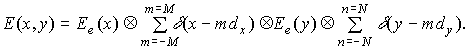 (12)
(12)
That coincides expression (3). That is there
is the inverse transformation of one-dimensional object in
two-dimensional object.
For confirmation this we made following experiment.
In optical scheme represented on fig.9 a periodic object (fig.10a)
are located. Since the periodic object had two axes of symmetry
therefore in optical scheme also is used two beams of coherent
radiation.
On photo presented on fig.10b. the result
of this synthesis is demonstrated As we see in fig.10b. the
image in nonzero diffraction orders is similar to image to
zero order.
But there is and difference so for example
in images generated in nonzero orders of diffraction there
is not powerful coherent background, therefore they will be
more qualitative. Such scheme permits to obtain in one plane
four identical images that can be used in the systems of processing
information where is required small multiplicity of multiplication.
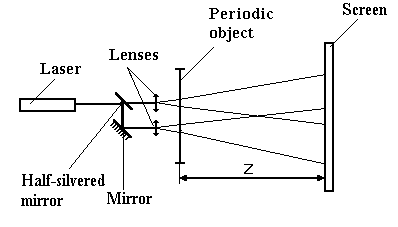
Fig.9. Optical scheme for synthesis of the
images of periodical object in nonzero diffraction orders.
|

|
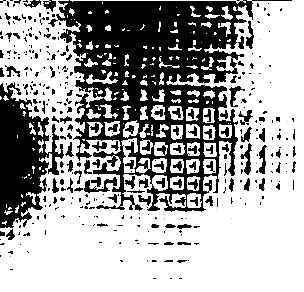
|
|
Fig.10a. Periodical object
|
Fig.10b. Synthesis of periodical object
images in nonzero diffraction orders.
|
-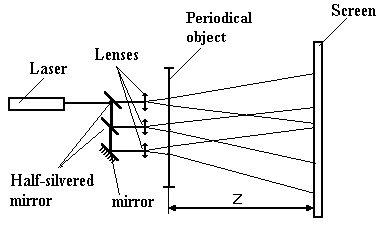
Fig.11. Optical schemes for contouring effect
obtaining of phase object. Z –Talbot’s distant.

Fig.12. Example of phase object contouring.
Other effect - contouring of phase objects
arise because in the field of geometrical shadow are interacting
nonzero diffraction orders containing the information on thin
structure of object. Hence, if the phase subject has smooth
change on D j
area and sharp change on edges, in nonzero diffraction orders
the information only about borders of object will be saved.
For confirmation of this effect we made the
following experiments. On fig.11. the optical scheme with
three laser beams is demonstrated. The quantity of laser beams
in optical scheme for contouring of phase objects in nonzero
diffraction orders depends on symmetry of periodic object.
If object has N of axes of symmetry hence for observation
of contouring effect in nonzero diffraction orders it is necessary
N of laser beams. In our particular case the object had three
axes of symmetry (matrix of triangles) therefore and is used
in scheme three beams of coherent radiation.
We see that in nonzero diffraction orders
in center of area where are overlaped three beams the image
of contours of individual elements of the phase object is
formed.
Conclusions.
On the basis of materials presented in this
article it is possible to make the following conclusions:
- Since the periodic object is not only image but also diffraction
grating there is the opportunity to transform image of subjects
from two-dimensional in one-dimensional and on the contrary
in nonzero the diffraction orders. That permits to use this
effect for multiplication of the images.
- Because of various speed of separation of the diffraction
orders there is the opportunity to make in nonzero diffraction
orders contouring of the elementary images of periodic objects
using the schemes offered in this article.
- The image which construct in nonzero diffraction orders
provided that the subject has rather thin structure of the
image and many of nonzero harmonics (about ten) has phase
which twice times less than phase of the image formed in
paraxial areasThat permits to obtain in one plane as negative
images, and positive images.
- Fresnel approach for description of an electromagnetic
field, diffracting on periodic object correctly only up
to the distance z=Ld/l ,
when all nonzero diffraction orders will separate among
themselves in space.
Reference
- Patorski K. The self-imaging phenomenon and its application./
Progress in optics, 1989, v.XXVII, p.3-108.
- Born M., Wolf E. Principles of optics - Oxford-London-Edinburgh-New
York-Paris-Frankfurt: Pergamon Press, 1964, 884 p.
- Andreev U.S., Sadovnik L.Sh., Tarnovethkiy V.V. The final
sizes influence of periodic objects to intensity of a Fresnel
images. /Opt. and Spect.(URSS), 1987, v.63,
№3, pp.620-627.
- Smirnov A.P. The influence the finite sizes of objects
on intensity of Fresnel images. /Opt. and Spect.(URSS),
1978, v.44, №.2, pp.359-365.
- Goodman J.W. Introduction to Fourier optics. San-Francisco:McGraw-Hill,
1968.- 364 p.
- Malov A.N., Feshchenko V.S. Hydrotipical Methods of Producing
of Relief Holograms. /In: II International Conference on
Microelectronics and Computer Science ICMCS'97. - Kishinev:
Tehnica Publishing House, 1997, v.2, p. 217-218.
- Porfiryev L.F. The principles of theory of the signal
transformation of in optic-electronic systems. Leningrad:
Mashinostroenie.-1989, 420p.

