Ждем Ваших писем...
   

 

ФИЗИКА ЛАЗЕРНОЙ БИОСТИМУЛЯЦИИ

Ю.В.Аграфонов, Ю.Н.Выговский1, Е.Я.Гаткин2, Я.С.Дорогобид, Л.Е.Кручинин3,А.Н.Малов3, С.Н.Малов3, В.Ю.Молоцило, О.О.Тимина4, В.С.Фещенко4, Л.В.Фещенко4

Иркутский государственный университет, Иркутск

1- НТФ “МеДиа”, Москва

2- НИИ педиатрии и детской хирургии МЗ РФ, Москва

3- Институт Лазерной Физики СО РАН, Иркутский филиал, Иркутск

4- Приднестровский государственный университет, Тирасполь

 

MeDia

Москва

2000

 

 

Рецензенты:

Доктор физико-математических наук, профессор, главный научный сотрудник Института Общей Физики РАН, В.В.Черный

Кандидат физико-математических наук, ведущий специалист Лаборатории Лазерной Медицины Научно- Исследовательского Клинического Института (МОНИКИ) Д.А.Рогаткин.

 

Рассматриваются на- основе квантово-радиофизических и синергетических представлений причины лазерной стимуляции биосистем. Взаимодействие лазерного излучения с биотканью анализируется, как самоорганизующийся процесс неадиабатического возмущения квазичастиц - конформеров и, с другой стороны, как явление самоподстройки распределения интенсивности лазерного излучения к клеточной структуре биоткани за счет эффекта Тальбота. Обсуждаются новые экспериментальные и теоретические результаты, подтверждающие значимость регулярной компоненты структуры электромагнитного поля и примембранных квазикристаллических структур биожидкостей в процессе взаимодействия лазерного излучения с биотканью.

Предназначено для студентов, аспирантов и научных работников в областях физики, биофизики, биологии, медицины и радиофизики.

 

© МеДиа, 2000.

 

Содержание

 

1.

Введение

4

2

Самоорганизация и неравновесность при ЛБС

5

3

Биологическая электродинамика

8

4

Природа центров светочувствительности

14

5

Теория граничных структур

17

6

Структура примембранной воды

22

7

Сенситометрические критерии степени фотомодификации крови

26

8.

Статистическая физика биологических процессов

35

9.

Нелинейная динамика при ЛБС

42

10.

Модовая концепция для описания эффекта ЛБС

45

11

Оптика биологических структур

61

12

Генерализация локального процесса ЛБС

65

13

Заключение

68

14

Благодарности

69

15

Список литературы

69

 

1. Введение

Феномен лазерной биостимуляции (ЛБС) широко используется в медицинской практике, хотя его сущность и механизмы еще далеко не полностью раскрыты и поняты [1]. Имеющаяся литература по ЛБС и лазерной терапии [1-3] по степени внятности объяснения причин эффективности для биосистем лазерного воздействия напоминает магико-астрологические и экстрасенсорные публикации. К основным неясностям относятся, во-первых, избирательность действия лазерного излучения только на “больные” клетки и биосистемы, и, во-вторых, наличие практически одинакового терапевтического эффекта для лазерного излучения с самой различной длиной волны. И, наконец, непонятно почему электромагнитное возмущение тонкого биохимического механизма, состоящего более чем из 10 000 звеньев (ферментов и белковых молекул) ведет к положительному результату, а не к простому нарушению работы тонкой биологической “машины” [4-6].

Биологические проблемы всегда привлекали внимание физиков [7]. Понятийный аппарат теории поля, эффективно используемый в физике, начал еще в 30-х годах внедряться в теоретическую биологию [8]. Теория когерентности световых полей в виде голографической концепции и ряд понятий квантовой механики находят свое приложение в современной генетической теории [9]. Нелинейно-динамическая теория солитонов применяется для описания возбужденных состояний биологических макромолекул типа ДНК и РНК [4]. Кибернетический и радиофизический подходы были плодотворно использованы для разработки концепции КВЧ-терапии [10]. Очевидно, что и такая экзотическая физическая концепция, как геометродинамика [11] с неизбежностью будет использована для описания структуры биологических объектов и явлений.

Специфика биологических исследований заключается в том, что яркая индивидуальность и сложность объектов, как правило, исключает совпадение их количественных характеристик [10]. Организация экспериментальных исследований и теоретическая интерпретация подобных результатов представляются весьма интересными и с точки зрения физики, поскольку они могут способствовать выработке новых концепций и методик. Один из перспективных в этом направлении подходов состоит в рассмотрении биоткани как особого когерентного состояния вещества [12]. Действительно, можно сказать, что живые объекты проявляют квантовые свойства: наблюдается, например, зависимость их характеристик от процедуры измерения и нелинейно-динамическое поведение биосистем [13].

Настоящее учебное пособие преследует цель сформулировать на основе физических концепций описание процесса взаимодействия лазерного излучения с биологическим веществом и показать, что эффект ЛБС может быть объяснен хотя бы качественно в рамках известных современных физических понятий.

2. Самоорганизация и неравновесность при ЛБС

Многообразие проявлений эффекта лазерной биостимуляции (ЛБС) - от молекулярно-биохимического уровня до целостных организменных реакций, с одной стороны, и почти полное подобие отклика биосистем различного типа на лазерное воздействие в диапазоне длин волн от КВЧ (30-300 ГГц) до ИК (до 400 ТГц) и видимого (400-800 ТГц) диапазонов, с другой стороны, с неизбежностью требует построения единой физической концепции взаимодействия когерентного излучения с биообъектами.

Экспериментально было установлено, что лазерное излучение действует и на отдельную клетку [2], а не только на биологические клеточные структуры [3]. Неоднократные попытки установления соответствия энергетических уровней атомов или молекул с энергией действующего светового кванта или поиски светочувствительного агента в биоткани не привели к положительным результатам, что, по-видимому, связано с недостаточным учетом степени “открытости” биологических систем в смысле статистической физики. Открытые системы в отличие от идеализированных замкнутых (изолированных) систем обмениваются со своим окружением веществом, энергией и, что особенно важно, информацией [14]. Поэтому в открытых системах, каковыми являются и живые системы, при взаимодействии с когерентным излучением, испускаемым существенно неравновесной активной средой лазера (имеющей инверсную населенность энергетических уровней), наряду с процессами тепловой деградации, могут происходить и процессы самоорганизации, в результате чего, в частности, происходит восстановление функций поврежденной биосистемы. Важной чертой эффекта ЛБС является эквифинитность: при широком варьировании исходных характеристик лазерного излучения конечный терапевтический эффект оказывается одинаковым.

Биологические системы являются не только открытыми, но и состоят из активных малых объектов (“квазичастиц”), структура которых сложна и недостаточно определена. По-видимому, конкретизация понятия элемента таких активных открытых систем существенно зависит от постановки задачи и требует учета коллективных взаимодействий в процессах самоорганизации, что изучает новая наука - синергетика. Сложное и нелинейное динамическое поведение и неполнота задания микросостояний в отдельных системах ансамбля делают применение статистического описания неизбежным [14].

Биологические системы состоят, очевидно, из большого числа “частиц”. Однако при построении модели биологической системы не следует оперировать такими понятиями, как атом, молекула или макромолекула. Целесообразно, по-видимому, ввести понятие особого типа квазичастиц - “конформеров”. Примерами таких квазичастиц можно считать отдельные конформационные состояния макромолекул [5]; давыдовские солитоны, бегущие по нити ДНК [4], экситоны и биэкситоны, возникающие в квазижидкокристаллической среде и др. Невозможность использования в теории эффекта ЛБС макромолекул как элементарных образований подтверждается и тем, что значительную роль при этом может играть и окружение молекулы (в виде, например, гидратных оболочек), так и необходимость учета влияния граничных условий (стенок клетки) на спектр допустимых конформационных состояний биомакромолекулы. Так, в статистической физике полимеров [15] показана возможность описания свойств макромолекулы, помещенной в трубке или щели малой толщины, как системы блобов, размер, которых определяется тем, что внутри блоба цепочка звеньев макромолекулы остается невозмущенной.

Наличие иерархичности в многоуровневой структурной организации биологических систем указывает на возможность взаимопревращений перечисленных и других типов “квазичастиц”. Такие превращения могут описываться с учетом свойств масштабного подобия биологических структур (фрактальность строения).

Использование статистического описания [16] показало, что процесс взаимодействия лазерного излучения с биовеществом имеет неадиабатический характер, обусловленный узкополосным (монохроматическим) характером спектра излучения. Второстепенное значение при этом имеет абсолютное значение длины волны лазерного излучения и иных начальных условий типа пространственной структуры волнового фронта. Воздействие на биосистему излучения обычных источников аналогично адиабатическому повышению температуры всей системы в целом, а действие монохроматического узкополосного лазерного излучения можно до определенной степени уподобить механическому перемешиванию биожидкости.

Принципиальным вопросом является определение физических параметров, описывающих систему и, по-видимому, для эффекта ЛБС можно использовать понятие производства энтропии, которое введено в неравновесной термодинамике на основе принципа Пригожина. Важным преимуществом энтропийных характеристик является их связь с информационными и структурными параметрами, например, в системе когерентного излучения, взаимодействующего с биосистемой. Эффект ЛБС можно, таким образом, рассматривать как совокупность неравновесных фазовых переходов, формирующих процесс самоорганизации, при котором система “когерентный свет - биовещество” идет по пути уменьшения производства энтропии. Следует заметить, что принятое в неравновесной статистической физике описание процесса самоорганизации, формирующегося из временной последовательности стационарных состояний, не всегда соответствует реальным биологическим стадиям [17], что может быть связано с взаимопревращением “квазичастиц”.

Другим аспектом эффекта ЛБС, относящимся к явлениям самоорганизации, является подстройка пространственно-временной структуры волнового фронта излучения к структуре биоткани, происходящая за счет оптических свойств клеточной структуры [18]. Существенным при этом оказывается то, что световое поле, образующееся в толще биоткани, практически не зависит от исходной структуры падающего лазерного излучения. Модовая структура поля когерентного излучения, распространяющегося в клеточной структуре, может обуславливать проявления эффектов Тальбота и Лауэ, приводящих к саморепродукции изображений и “самоисправлению” клеточных элементов структуры. На основе модовой теории изображений и теории информации могут быть определены и различия между одномоментным и сканирующим облучением биоткани в лазерной терапии.

Попытки установления соответствия энергетических уровней атомов или молекул с энергией действующего светового кванта или поиски светочувствительного агента в биоткани не привели к положительным результатам, что, по-видимому, связано с недостаточным учетом степени “открытости” биологических систем. Открытые системы в отличие от идеализированных замкнутых систем обмениваются со своим окружением веществом, энергией и, что особенно важно, информацией. Биологические системы являются не только открытыми, но и состоят из активных малых объектов, структура которых сложна и недостаточно определена. По-видимому, конкретизация понятия элемента таких активных открытых систем существенно зависит от постановки задачи и требует учета коллективных взаимодействий в процессах самоорганизации, в отличие от использования понятия “макромолекула”, которое, по определению, учитывает в первую очередь химические свойства вещества.

Биологический объект представляет собой наиболее сложную в оптическом и структурном отношении систему. В ней, по-видимому, реализуются все, рассмотренные выше явления, и, кроме того, существенную роль играют динамические характеристики организма. Двойственность биосистем, для которых характерны явления, определяемые исключительно свойствами или отдельных микросистем, их внутренним строением, или макросистем, но при условии, что они проявляют себя как целое, и явления, которые не зависят от строения микроскопических частиц и специфических взаимодействий между ними, а, следовательно, и от конкретных механизмов протекания процессов. Последние явления обусловлены интегральными свойствами характеристического ансамбля с колоссальным числом “безликих” и независимых друг от друга участников, что описывается в терминах термодинамики и статистической физики. Несомненную фундаментальную проблему создает и эволюционно сформировавшееся наличие в нативных конформациях биологических макромолекул согласованности ближних, средних и дальних взаимодействий [19.]. Ситуацию в биосистемах усложняют как отсутствие строгой границы между этими явлениями, так и открытость и неравновесность таких систем.

На настоящий момент описание явлений, например, в клетке имеет мозаичный характер: первичный акт взаимодействия фотона с макромолекулой должен описываться квантомеханически, изменение конформационного состояния макромолекулы описывается в рамках квантовой химии и биохимии [5], структура макромолекулы в целом описывается на основе статистической теории П.Флори, взаимодействие макромолекул описывается в рамках детерминистических моделей типа “замок-ключ”, “рука-перчатка”, а поведение, например, клетки в целом описывается на основе теории автоматов и систем [20]. Кроме этого, по мере необходимости, во внимание принимаются и теории фазовых переходов и самоорганизации [13, 15]

Эффект ЛБС является нетривиальным примером взаимодействия двух неравновесных систем: когерентного поля и биологической системы. Несмотря, казалось бы, на необходимость “резонанса” этих двух систем по длине волны для возникновения взаимодействия, оно происходит всегда при монохроматичности излучения, что связано, видимо, с дискретностью энергетического спектра биосистемы и с изменением ее параметров во времени - она “дышит” и, тем самым, всегда обеспечивает резонанс структур. Основными чертами этого взаимодействия следует считать наличие самоорганизации и эквифинитности - независимости конечного результата от меняющихся в широких пределах начальных условий (длина волны, угол освещения, интенсивность и др.). Предложенный подход показывает, что казалось бы, далекие друг от друга физические картины типа хаотизации через бифуркации и теплового нагрева излучением могут быть синтезированы в едином описании [21].

3. Биологическая электродинамика

Отдельная клетка как объект исследований характеризуется сложной пространственно-геометрической архитектурой (рис. 1), не говоря уже о сложности ее молекулярно-динамической организации [5,6,17]. Невозможность непосредственного использования для описания клетки классической электродинамики обусловила чисто качественную направленность концепции биополя [8] в теоретической биологии. Это связано с тем, что в условиях клетки реализуется именно та ситуация, в которой невозможно использовать аппарат теории поля [22]. А именно, заряд (или система зарядов), находящийся в поле, не только подвергается воздействию со стороны поля, но, в свою очередь, и сам влияет на поле, изменяя его. Тем не менее, имея в виду эти принципиальные ограничения, для анализа биологических систем понятия классической электродинамики могут использоваться хотя бы в виде языка, а не численных характеристик.

Дипольный момент системы зарядов вводится при рассмотрении поля от системы зарядов на расстояниях, значительных по сравнению с размерами системы, что в клетке, вообще говоря, не выполняется. Тем не менее, по определению [22], потенциал в точке 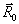поля, создаваемого системой зарядов qi с радиус-вектором каждого заряда 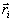, равен

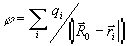(1)

и если R0 >>ri то, возможно использовать разложение

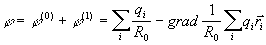. (2)

На основании последнего выражения и вводится понятие дипольного момента системы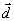

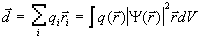(3)

где 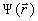- волновая функция системы зарядов, определяемая квантовомеханически. С математической точки зрения при разложении (1) по степеням R0 более корректно учитывать все члены ряда

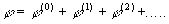(4)

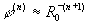где . (5)

Если система электронейтральна и не имеет дипольного момента, т.е.

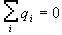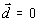и , (6)

то при анализе ее поля надо учитывать третий член разложения в (4) - квадрупольный потенциал:

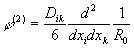, (7)

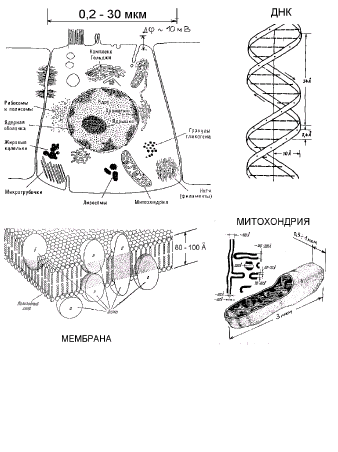
Рис.1. Схематическое изображение строения клетки.

1 мкм = 1000 нм = 10 000 Å . Длина волны излучения гелий-неонового лазера 630 нм = 0,63 мкм.

где Dik - тензор квадрупольного момента. Можно показать [22], что l-й член разложения (4) определяется тензором 2l -польного момента l-го ранга, симметричным по всем своим индексам и обращающимся в ноль при свертывании по любой паре индексов. Квадрупольный момент системы не зависит от выбора начала координат, если выполнены условия (6). В отличие от классической электродинамики при анализе поля в клетке необходимо, видимо, учитывать и квадрупольные и более высокие моменты биомакромолекул, что, конечно, делает нереальным численный расчет характеристик поля.

Основной чертой биохимических процессов в клетке является их электронно-конформационный или матричный характер [5]. Изменения конформационного состояния макромолекул при, например, их “свертывании” или развертывании, требуют малых энергий, но приводят к значительным вариациям в их каталитической активности. Известные модели [23] ферментативного катализа, такие как “ключ-замок”, “рука-перчатка”, “дыба” и “белок-машина”, основаны на необходимости обеспечения комплементарности конформационных состояний субстрата и фермента. Конформационный характер взаимодействия биохимических реагентов обуславливает энтропийный тип этих реакций. Или, иными словами, их направленность на изменение и согласование вторичной, третичной и т.д. структур - конформаций биомакромолекул по отношению друг к другу. Ограниченность ресурса биомакромолекул в пределах клетки и необходимость поддержания достаточного для жизнедеятельности количества макромолекул в заданном конформационном состоянии привели к возникновению в процессе эволюции специализированного механизма селекции или перевода молекул в нужное конформационное состояние. С точки зрения лазерной физики этот механизм можно рассматривать как систему “накачки”, обуславливающую статистическую неравновесность всей биосистемы. С квантово-механической точки зрения подобная неравновесность может рассматриваться как причина когерентного состояния биовещества и биосистем [12,14].

Механизм “накачки” или отбора нужных конформационных состояний макромолекул может быть описан в рамках теории электромагнитного поля хотя бы на понятийном уровне, поскольку корректное использование привычного математического формализма затруднительно. Основной физической характеристикой биомакромолекулы, связанной с ее конформационным состоянием, можно считать дипольный (см. ур.(3)) и/или мультипольный момент. Биомакромолекулы взаимодействуют с электрическим полем световой волны, меняя свое энергетическое состояние за счет изменения ориентации и величины своего дипольного момента. Степень эффективности такого взаимодействия можно оценить параметром a , являющимся мерой потенциальной энергии диполя 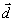в электрическом поле напряженностью :

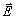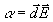(8)

Следует отметить, что дипольный (мультипольный) момент биомакромолекул или ее почти независимых участков - блобов, доменов [15,17] - в общем случае отличен от нуля хотя бы из-за наличия температурных флуктуаций.

Поскольку любая физическая система стремится к минимизации своей потенциальной энергии, то можно предположить, что конечный продукт любой биохимической реакции должен иметь минимальный собственный дипольный момент хотя бы из-за наличия внутриклеточного поля ненулевой величины. Поэтому в процессе реакций белкового синтеза реагенты имеют различные дипольные моменты и поле клетки может управлять их поведением и, по окончании реакции, они взаимно компенсируются в максимально возможной степени. Диполь - дипольное взаимодействие реагентов при синтезе

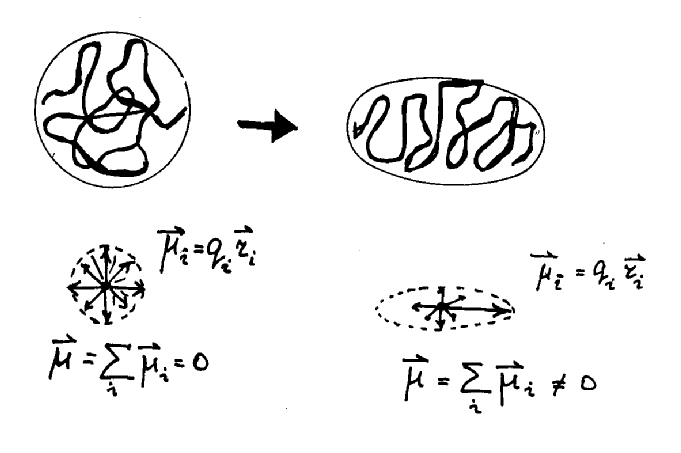
Рис.2. Увеличение дипольного момента молекулы при ее планаризации.

обеспечивает комплементарность субстрата и фермента, а также обеспечивает более эффективное по сравнению с конечным продуктом их взаимодействие с электромагнитным полем лазерного излучения, что ведет к стимуляции различных реакций синтеза, например, ДНК и РНК [2]. Это можно представить следующим образом: в результате дипольного взаимодействия макромолекулы с полем ее энергия повышается, что приводит к интенсификации процесса “перебора” различных конформационных состояний и более быстрому “нахождению” комплементарного для другого реагента конформационного состояния.

Нарушение функционирования клетки, по-видимому, в первую очередь вызывает накопление излишних продуктов биологических реакций и для их выведения за пределы клетки реализуется увеличение поверхностной площади мембраны, что проявляется как возникновение выпуклостей, отростков и общей гофризации клеточной мембраны. Попавшая в такой “карман” объемная клубкообразная биомакромолекула неизбежно “сплющивается”, становится преимущественно двумерным образованием, что, в свою очередь, ведет к увеличению ее собственного дипольного момента (рис. 2). А в дипольном приближении [24] эффективность взаимодействия с электромагнитным полем описывается уравнением (8). Поэтому рост дипольного момента у молекул приводит к увеличению ее светочувствительности. Или, иными словами, “болезнь” сенсибилизирует клетку и обеспечивает селективность ЛБС. Это простое физическое соображение, хорошо известное, например, в области синтеза органических фоторегистрирующих сред [25], объясняет, кроме повышенной эффективности процесса ЛБС для дефектных клеток, и часть причин, приводящих к различию лазерных экспериментов в биофизике в условиях in vivo и in vitro. Многочисленные данные о лазерной стимуляции различных ферментов также, по-видимому, связаны с подобным уплощением пространственной структуры биомакромолекул, поскольку каталитический центр многих ферментов также находится в глубине достаточно узкого “кармана” [15]. Можно заметить, что клетки, специализирующиеся на фоторецепции, имеют в своем составе именно плоские структуры типа дисков и ламеллей (рис. 3), что также подтверждает необходимость “планаризации” структуры молекулы для повышения ее светочувствительности [5].

Максимальная амплитуда электрического вектора 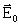(В/см) световой волны с интенсивностью I (Вт/см2) определяется выражениям для линейно поляризованного излучения [24]:

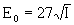, (9)

а для излучения с круговой поляризацией

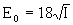(10)

Из этих известных соотношений прямым образом следует и наличие зависимости эффекта ЛБС от характера поляризации лазерного излучения, даже без учета ориентации клеточной структуры, что отрицается рядом исследователей [2].

Используя эти соотношения, можно также предположить, что пороговая величина интенсивности лазерного излучения, еще вызывающая ЛБС, должна быть сравнима с напряженностью электрического поля, окружающего объект воздействия [3]. Реальные биосистемы (в т.ч. человек) функционируют в условиях наличия атмосферного электрического поля, средняя величина которого составляет около 100 В/м и может значительно меняться в течение суток - от +600 В/м до -600 В/м [26], и полей, обусловленных техногенными факторами. Не конкретизируя механизмов управления биологическими процессами за счет клеточных электромагнитных полей, можно предположить, что атмосферное электрическое поле определяет величину шумов для таких управляющих систем. Поэтому электрическое поле световой волны, вызывающей ЛБС, должно превышать, согласно (9)-(10), значение 10-4 мВт/см2 (если считать диэлектрическую проницаемость биоткани равной 50), что соответствует и известным медико-экспериментальным данным. Корректность введения такого критерия нуждается, конечно, в сопоставительном анализе данных по ЛБС и данных о напряженности атмосферного электрического поля во время проведения процедур лазерной терапии. Также, по-видимому, в качестве критерия для глубины проникновения лазерного излучения в

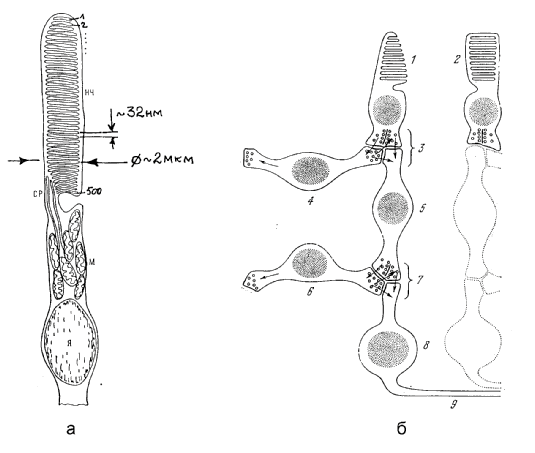
Рис.3. а). Схема строения палочки сетчатки позвоночных: НЧ - наружный членик, СР - соединительная ресничка, М - митохондрии, Я - ядро.

б). Схема синаптических контактов между клетками сетчатки. 1 - колбочка, 2 - палочка, состоящие из дисковых органелл, служащих для улавливания фотонов, 3 - внешний синаптический слой, 4 - горизонтальная клетка, 5 - биполярная клетка, 6 - амакриновая клетка, 7 - внутренний синаптический слой, 8 - ганглиозная клетка, 9 -аксон зрительного нерва [5].

биоткань следовало бы использовать величину, соответствующую напряженности атмосферного электрического поля с учетом диэлектрических свойств биоткани.

Следует отметить, что дипольное приближение (8) является достаточно грубым приближением для таких сложных объектов, как биологические макромолекулы и их объединения, и поле, наводимое ими, будет иметь в качестве источников так называемые фрактальные токи конформеров. Характеристики последних определяются конкретными распределениями процессов пространственно-временной диффузии продуктов первичной фотохимической реакции и могут быть в какой то степени описаны в рамках фрактальной теории [27, 28].

4. Природа центров светочувствительности

С квантово-механической точки зрения взаимодействие излучения с веществом есть резонансное явление, соответствующее равенству энергии фотона энергии перехода системы. Поэтому всегда необходимо, при наличии взаимодействия, найти материальную систему с соответствующей разностью энергий. Это оказывается зачастую нетривиальной задачей. Так, например, в случае лазерной биостимуляции красным излучением таких объектов (с химической точки зрения) просто нет. Скорее всего, это связано с тем, что молекула (в химическом смысле) не есть минимальная частица живого вещества – она, конечно, сохраняет химические свойства данного соединения, но самостоятельно не живет.

Одной из первых эффективных методик по применению лазеров в медицине оказалось внутривенное облучение крови (ВЛОК). Форменные элементы крови обладают высокой конформационной лабильностью и, по-видимому, способны к кооперативным взаимодействиям, поскольку для продвижения по микрокапилярным сосудам должны очень сильно деформироваться [29]. Способность к кооперативным взаимодействиям и объясняет, по-видимому, возможности крови по “подстройке” к монохроматическому излучению в широком диапазоне длин волн[3,29].

От элементарной (первичной) фотохимической реакции до полного описания результатов процесса взаимодействия излучения с объектом лежит достаточно большая дистанция, если иметь в виду реализацию конкретных информационных или медицинских устройств. Особую сложность представляет описание поля в рассеивающих, биоподобных и иных сложно структурированных средах. Если же среда распространения излучения оказывается “живой” или фоточувствительной (как в голографии), то ситуация становится почти безнадежной и может быть разрешена исключительно экспериментально. Также с большим трудом пока решается проблема описания и исследования т.н. сингулярных волновых фронтов (спиральных, спекл и дислокационных пучков излучения); попытки фрактального описания подобных волновых структур пока не привели к решению задач формирования полей с заранее заданными параметрами.

С точки зрения классической (и квантовой) электродинамики причины взаимодействия излучения и вещества связаны с наличием дипольного (или более высокого порядка) момента у вещества и с достаточной по величине интенсивности концентрации излучения в этом же месте. Поэтому, с одной стороны, необходимо знать структуру волнового поля в области взаимодействия, а, с другой стороны, при наличии факта взаимодействия выяснить причины образования или наличия дипольного момента. Будем называть локальные области концентрации поля по интенсивности сингулярностями излучения, а места локализации дипольного момента – сингулярностями или центрами светочувствительности (ЦСЧ) вещества.

В случае, например, конструирования среды для фотографической или голографической регистрации информации стремятся достичь равномерного распределения по всему объему сингулярностей или ЦСЧ вещества. Это оказывается возможным, если ЦСЧ являются макромолекулы или их отдельные участки, что характерно для коллоидных регистрирующих голографических сред и, в некоторой степени, для биологических объектов, как будет рассмотрено ниже. Своеобразные ЦСЧ реально могут возникать и естественным образом, в частности, благодаря граничным слоям жидкости, как это имеет место вблизи биологических мембран или вблизи подложки, на которую наносится светочувствительная полимерная эмульсия. Заметим, что в свое время мембраны предлагалось рассматривать как основное звено в механизме взаимодействия КВЧ-излучения с живыми организмами [10], но при этом не в полной мере учитывалась роль именно граничных структур.

Использование терминологии и подходов из теории фотографического процесса [74] представляется достаточно удобным и адекватным для описания процессов взаимодействия излучения со сложными объектами. За время своего более чем полуторавекового развития фотографическая наука выработала, хотя и эмпирический, но практически адекватный формализм типа сенситометрического описания светочувствительных материалов и процессов, вполне применимый не только в голографии, но и в биооптике.

Сингулярности объекта как центры светочувствительности

Граничные слои и пленочные структуры. Физические свойства пленок существенно отличаются от свойств объемных образцов из того же вещества, что связано с влиянием, как свободной поверхности, так и границы между пленкой и подложкой на процесс формирования пленки [30]. Поверхностные и граничные слои часто характеризуются дальним порядком расположения ориентированных молекул [31], что ведет к образованию ориентированных квазикристаллических макроструктур [32]. Экспериментально было установлено еще в 1930г., что формирование ориентированных граничных слоев происходит в случае контакта поверхностно-активных веществ с поверхностью твердого тела. Это обстоятельство широко используется в способе Ленгмюра-Блоджета для формирования мономолекулярных слоев полярных молекул на неорганических подложках для сверхразрешающей нанолитографии [33] и для получения мультимолекулярных слоев (Y-пленок) [31].

Другим примером реального использования ориентированных граничных слоев органических жидкостей являются смазывающие процессы [31]. Исследования в этой области показали, что силовое поле твердого тела не экранируется первым слоем молекул жидкости . Но ориентация молекул полярной жидкости в первом приграничном к твердой поверхности слое играет роль “затравки”, организующей ориентацию последующих слоев. Механизмом, реализующим этот эффект, может являться взаимодействие молекулярных диполей с образованием нейтральных в целом “цепочек”, перпендикулярных к поверхности контакта. Подобные соображения стали основой эмпирической поляризационной теории де Бура и Цвиккера [31], показавшей как локальное короткодействие, распространяясь в жидкости путем индуцирования дипольных моментов в соседних слоях, порождает дальнодействующие силы, упорядочивающие большие объемы вещества. Поэтому в граничных слоях структура жидкостей изменяется по сравнению с объемной, и тем сильнее, чем выше ее полярность и размер молекул растворенного в ней вещества. В то же время, граничные слои переходят по мере удаления от твердой подложки в объемную жидкость, что делает актуальной задачу адекватного описания и этого явления.

5. Теория граничных структур.

А. Классический подход на основе теории жидкости. Принципиальная возможность теоретического исследования структуры неоднородной жидкости вблизи поверхности определяется нахождением решения совместной системы уравнений для одночастичной и двухчастичной функций распределения, причем существуют несколько исходных эквивалентных точных систем уравнений [34]. Их прямое применение даже для простых систем сферически - симметричных молекул требует огромных усилий [35,36]. Упростить задачу можно, если в уравнении для профиля плотности вместо анизотропной двухчастичной функции распределения использовать обычную объемную двухчастичную функцию распределения. Такая процедура не является однозначной. В зависимости от того, в какой исходной системе уравнений или каким способом производится упрощение, можно получить различные синглетные уравнения для профиля плотности, точность которых можно оценить лишь по конечным результатам.

Наиболее распространенным является подход, при котором рассматривается смесь двух компонент, в которой размеры одной из компонент становятся как угодно большими. Тогда в пределе нулевой концентрации этой компоненты функция распределения между двумя компонентами рассматривается как одночастичная функция распределения ненулевой компоненты вблизи поверхности. В работе [37] дан анализ существующих синглетных приближений, из которого видно, что при малых и средних плотностях все синглетные уравнения являются удовлетворительными. При больших плотностях, однако, ситуация меняется. Физические решения имеются лишь для синглетных уравнений, получаемых из интегральной формы точных уравнений для одночастичной и двухчастичной функций распределения [38].

Исследование структуры дипольных систем как в объемном случае, так и тем более вблизи поверхности усложняется из-за наличия сложной ориентационной зависимости потенциала взаимодействия между молекулами. Применение метода интегральных уравнений в среднесферическом приближении для исследования объемной структуры дипольных твердых сфер, позволило выразить решение в полуаналитической форме, в которой угловая зависимость функций распределения представляется в виде определенных комбинаций тригонометрических функций. Это решение можно улучшить, используя другие замыкания уравнения Орнштейна–Цернике. В работе [39] было указано, что удобной для анализа формой решения является его представление в виде ряда по степеням параметра диполь - дипольного взаимодействия, что позволяет, с одной стороны, разделить угловые и радиальные переменные, с другой — получить зависимость функций распределения от дипольных моментов в явном виде.

Развиваемый в [36,40] подход, в котором также рассматриваются дипольные твердые сферы у твердой поверхности, отличается в следующих отношениях:

    1. Используется синглетное уравнение, вытекающее из интегральной формы точного уравнения для одночастичной функции распределения [38,39]. Только это уравнение имеет физическое решение для бездипольных твердых сфер вблизи поверхности при плотностях выше r=ns3=0.75 . (Здесь n=N/V - численная плотность, s - диаметр сферы).

    2. Решение для одночастичной функции распределения ищется в виде рядов по параметру диполь- дипольного взаимодействия, как это было сделано в работе [41] для двухчастичной объемной функции распределения.

    3. Расчеты ограничивались третьим порядком по параметру диполь- дипольного взаимодействия.

Отметим, что основной целью теоретического анализа является получение решений удобных для анализа и описания структурных особенностей, вызванных действием твердой поверхности на дипольную систему. Помимо теоретического значения, исследование систем с диполь- дипольным взаимодействием является важным для анализа структуры реальных жидкостей. так как наличие ориентационной части потенциала взаимодействия присуще большинству реальных молекулярных жидкостей. Точно так же изучение неоднородных систем важно для понимания свойств жидкости вблизи поверхности твердого тела, взаимодействия коллоидных частиц, поведения жидкостей в малых объемах.

Развиваемый подход является по существу одним из вариантов термодинамической теории возмущений, и ему, конечно, присущи все связанные с этим ограничения, но он позволяет получить хотя бы качественные оценки структурных и ориентационных эффектов, а для слабо дипольных систем предложенный подход является практически точным. Предложенный подход обладает достаточной общностью, и применим для описания различных связно-дисперсных систем, в которых фазы не могут перемещаться свободно, поскольку они структурно закреплены, например, в гелевой системе. Изложенный формализм применим для описания широкого класса структурно-граничных явлений таких, как фазовый переход расплав-кристалл в двухкомпонентной системе, расчет квантовых поправок к давлению на кривых фазового равновесия, кристаллизация Леннард-Джонсоновской жидкости и учет влияния структуры примембранной воды на эффект лазерной биостимуляции [40].

Б. Квантово-механический подход

В физике конденсированного состояния межмолекулярное взаимодействие входит в гамильтониан в виде амплитуды рассеяния в борновском приближении. Это приводит к необходимости осуществления перенормировки взаимодействия. Метод временных функций Грина позволяет вычислять только спектр элементарных возбуждений, по заданной энергии основного состояния, определяющему начальные условия для цепочки функций Грина. Энергия основного состояния определяется диагональными матричными элементами гамильтониана. Межмолекулярное взаимодействие входит в гамильтониан в виде амплитуды рассеяния в борновском приближении.

Для реальных потенциалов, учитывающих межмолекулярное отталкивание, борновское приближение непосредственно не применимо. Поэтому возникает необходимость осуществления перенормировки взаимодействия с тем, чтобы можно было применить теорию возмущений. Однако физический смысл констант перенормировки остается неясным. Целесообразно перейти к такой формулировке теории, в которую бы исходно входил потенциал межмолекулярного взаимодействия, а не амплитуда рассеяния. Тем самым термодинамические величины можно было бы вычислять не прибегая к теории возмущений.

Таким образом, возникает необходимость рассмотрения жидкостей как квантовых объектов с учетом сильного межмолекулярного взаимодействия. Система сильновзаимодействующих фермионов или бозонов может быть описана с помощью вигнеровских l-частичных функций. Простейшая из них – двухчастичная функция F12(r1, p1 ,r2 , p2), где ri , pi - координаты и импульсы частиц. Усредненная по импульсам частиц функция <F12(r1, ,r2 )> есть радиальная функция распределения, т.е. плотность вероятности обнаружения двух частиц в точках с координатами r1,,r2 . Набор l-частичных вигнеровских функций описывается бесконечной цепочкой зацепляющихся уравнений Боголюбова. Разработка методов решения таких уравнений до сих пор остается актуальной задачей. Трудность решения связана с тем, что необходимо учитывать классические и квантовые корреляции. Последние спадают с рассеянием гораздо медленнее. Поэтому обычно ограничиваются либо рассмотрением идеального квантового газа, либо учет межмолекулярного взаимодействия осуществляют в методе вторичного квантования в рамках борновского приближения. Для систем с реальными потенциалами межмолекулярного взаимодействия борновское приближение неприменимо, поэтому возникает необходимость перенормировки потенциала.

Вопрос заключается в том, на каком этапе проводить перенормировку. Такую возможность дает вигнеровская формулировка статистической механики. Уравнения для вигнеровских функций распределения (частичных матриц плотности) содержат непосредственно потенциал межмолекулярного взаимодействия. Эволюция функций во времени описывается бесконечной цепочкой уравнений, аналогичной цепочке уравнений для функций Грина. Долгое время считалось, что уравнение для одночастичной функции Вигнера неправильно, так как оно не описывает квантовый осциллятор. По этой причине вигнеровское представление не получило широкого применения. Впоследствии было выявлено, что уравнение для одночастичной функции Вигнера должно быть дополнено "эволюционным" уравнением, которое должно правильно учитывать начальные условия. Это обстоятельство является существенным для вычисления спектра элементарных возбуждений. Однако для расчета энергии основного состояния это не имеет значения, так как последняя определяется через равновесные решения. Поэтому мы предлагаем в основу теории положить цепочку уравнений для термодинамически равновесных вигнеровских функций. При этом независимой переменной будет плотность частиц.

До сих пор считалось, что решение уравнений для равновесной цепочки интереса не представляет (и в литературе оно не описано), так как энергию основного состояния можно найти в рамках теории нормальной ферми-жидкости Ландау. Однако, реально в таких вычислениях используется борновское приближение. Таким образом, предлагаемый подход позволит снять ограничения, связанные с борновским приближением. А именно, мы предлагаем рассматривать уравнение для <F12(r1, ,r2 )> в приближении парных столкновений. В этом случае для <F12(r1, ,r2 )> получается замкнутое уравнение, которое может быть решено аналитически. Перенормировка потенциала должна проводиться именно в этом решении. После такой процедуры возможно получить обобщение на случай систем с произвольной плотностью по аналогии с классическим уравнением Орнштейна-Цернике.

В результате и классические и квантовые системы можно описывать на основе единого формализма с помощью радиальной функции распределения, задающей ближний порядок в жидкостях. Такой подход позволяет описывать термодинамические и структурные параметры в квантовых газах и жидкостях, в том числе и фазовые переходы, по заданным плотности, температуре и потенциалу межмолекулярного взаимодействия.

Механизм светочувствительности биологических систем. Анализ явления ЛБС с точки зрения современных физических концепций приводит к выводам о том, что ,во-первых, процесс содержит в себе множество различных механизмов воздействия когерентного излучения на биологические системы, и, во-вторых, к необходимости рассмотрения процесса ЛБС как самоорганизующегося динамического взаимодействия открытой, статистически неравновесной, биосистемы с когерентным излучением, что, в свою очередь, требует учета взаимодействия динамических и информационных аспектов поведения сложных систем.

Основной чертой биохимических процессов в клетке является их электронно-конформационный или матричный характер [20]. Изменения конформационного состояния макромолекул при, например, их “свертывании” или развертывании, требуют малых энергий, но приводят к значительным вариациям в их каталитической активности. Известные модели [20] ферментативного катализа, такие как “ключ-замок”, “рука-перчатка”, “дыба” и “белок-машина”, основаны на необходимости обеспечения комплементарности конформационных состояний субстрата и фермента. Ограниченность ресурса биомакромолекул в пределах клетки и необходимость поддержания достаточного для жизнедеятельности количества макромолекул в заданном конформационном состоянии привели к возникновению в процессе эволюции специализированного механизма селекции или перевода молекул в нужное конформационное состояние. С точки зрения лазерной физики этот механизм можно рассматривать как систему “накачки”, обуславливающую статистическую неравновесность всей биосистемы. С квантово-механической точки зрения подобная неравновесность может рассматриваться как причина когерентного состояния биовещества и биосистем [12,14].

.

Граничные слои и структуры при ЛБС. Сэндвичевые структуры дипольных жидкостей вблизи биомембран [43] также оказываются пространственно согласованными с самоорганизованным Тальбот-полем лазерного излучения в биоткани. Из уравнений Боголюбова - Борна - Грина - Кирквуда - Ивона могут быть получены интегральные уравнения для профиля плотности воды вблизи поверхности мембраны и описана структура дипольной системы неоднородной жидкости вблизи поверхности при наличии сложной ориентационной зависимости потенциала взаимодействия между молекулами. Чередование водных слоев с различной преимущественной ориентацией диполей вблизи мембраны влияет как на процессы свертывания - развертывания белковых макромолекул, так и на их сенсибилизацию к действию электромагнитного излучения. Такая структурная организация примембранной жидкости не позволяет рассматривать процесс ЛБС и как термодинамически равновесный, а требует привлечения аппарата теории статистической физики открытых систем. Поэтому, в целом взаимодействие лазерного излучения с биоструктурами является самоорганизующимся процессом неадиабатического возмущения системы “мембрана - связанная вода - биомакромолекулы” и сказывается, в первую очередь, на эффективности синтеза новых биомолекул [44].

6. Cтруктура примембранной воды

Если в качестве элементарного биологического объекта рассматривать клетку, то естественным приёмником излучения являются клеточные мембраны, функционирование которых определяется ролью "пограничных структур", обеспечивающих избирательную проницаемость веществ в клетку, а также реагирование клетки на состояние окружающей среды. Биорегуляторная функция мембран сводится к восприятию внешнего воздействия на каком-либо локальном участке и передаче такого импульса на всю поверхность мембраны. После этого включается внутриклеточный механизм ответа на внешнее воздействие.

В основе структуры мембран находится липидный бислой, состоящий в основном из фосфолипидов (70-80% всех липидов мембраны). Молекула фосфолипида представляется следующим образом: некоторая полярная часть - радикал и неполярный двухцепочечный углеводородный хвост.

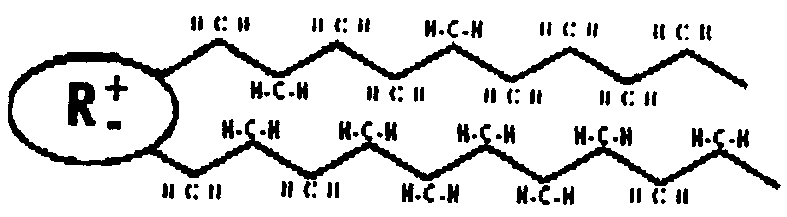
Рис.4. Схематическое изображение молекулы фосфолипида: полярный радикал и двойная углеводородная цепь (предельная).

В водной среде такие молекулы образуют термодинамически устойчивые структуры, где неполярные углеводородные цепи удалены от контакта с водной средой и формируют гидрофобную зону, а полярные концы - гидрофильную поверхность, взаимодействующую с водой.

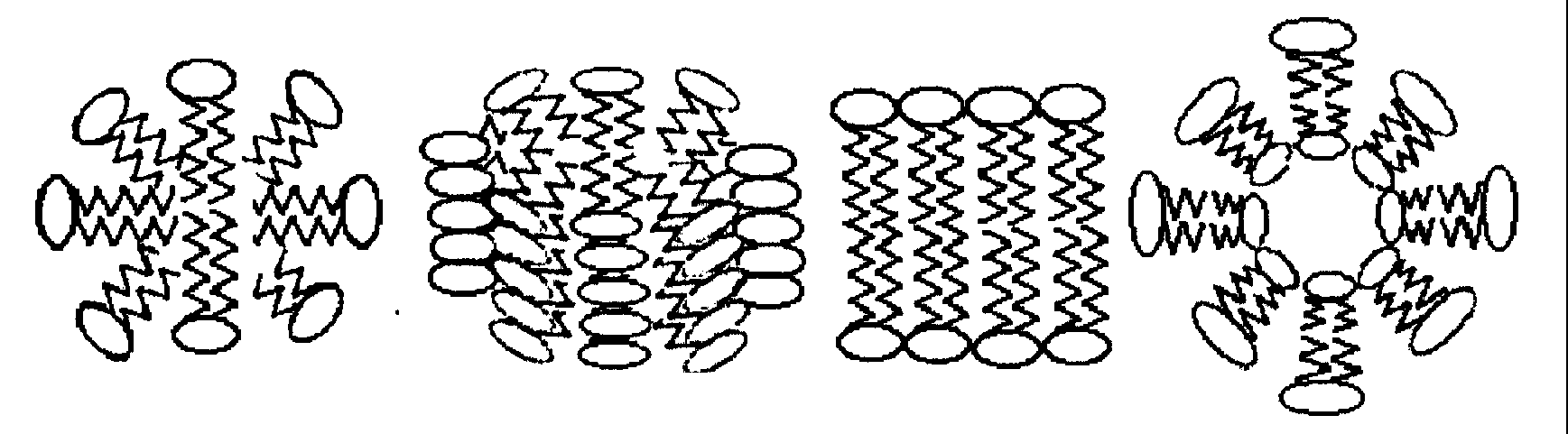
Рис. 5. Некоторые структуры, образуемые молекулами фосфолипидов в водной среде в результате гидрофобного взаимодействия.

Молекулы липидов способны вращаться вокруг собственной оси, перемещаться в плоскости бислоя ( линейная скорость порядка 5-10 мкм/с ), переходить из одного монослоя в другой ( время полуперехода порядка нескольких часов ). Таким образом, бислой динамичен и в нём осуществляется близкодействие между липидными молекулами.

Вместе с тем мембрана в целом характеризуется стабильностью и наличием эффектов дальнодействия, когда некоторое локальное внешнее возмущение передаётся на значительные межмолекулярные расстояния вдоль поверхности мембраны [46]. Поэтому была предложена модель мембраны, в которой ее регуляторная роль обуславливается сосуществованием двух структурно обособленных, но функционально объединённых матриксов: динамичного двумерного липидного бислоя и стабильного трёхмерного белкового каркаса, обеспечивающего дальнодействие. В результате мембрана имеет некоторую фрактальную размерность.

В рамках этой модели становится возможным объяснить векторность мембранных процессов, образование короткоживущих комплексов и ярко выраженное свойство кооперативности мембранных элементов, особо важное в процессах биоуправления.

В настоящее время считается, что первичным событием процесса биорегуляции является взаимодействие внешнего импульса ( фотона, сигнальной молекулы ) со специализированным белковым рецептором на поверхности мембраны. В образовавшемся комплексе белок испытывает конформационный переход на уровне третичной структуры ( это фазовый переход второго рода ), то есть возникает локальное структурное изменение мембраны.

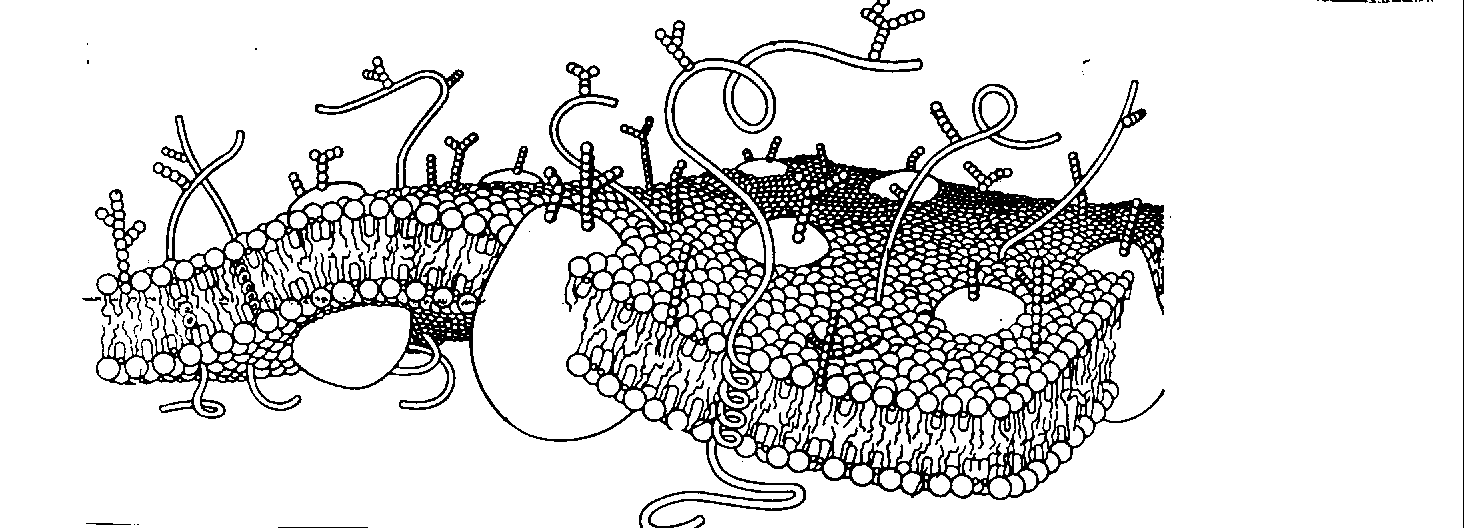
Рис. 6. Липидный бислой со встроеными комплексами глобулярных белков, образующих в результате взаимодействия жесткий каркас мембраны.

Возмущение генерализуется на всю мембрану, которая при этом рассматривается как кооперативная система, поддерживаемая взаимодействиями типа "белок - белок", "липид - липид" и "белок - липид" при участии воды. После завершения кооперативной перестройки мембраны скачком изменяется её функциональная активность и, как следствие, состояние клетки [43].

Распространение структурного возмущения вдоль поверхности мембраны, возможно, связано с наличием структурированной воды, которая имеет некую квазикристаллическую или льдоподобную структуру форму, сильно зависящую от окружающих биомолекул. В примембранных областях вода может структурироваться двояко. Это, во-первых, связывание у поверхности липидного бислоя как у ограничивающей поверхности и, во-вторых, структурирование вдоль цепи макромолекулы, а при наличии у молекулярной системы внутренней полости ( что возможно в случае глобулярного белка ) - внутри полости [45].

Для приближённого описания поведения жидкости у ограничивающей поверхности возможно использование статистического рассмотрения, основанного на уравнениях Боголюбова-Борна-Грина-Кирквуда-Ивона [36].

Для пространственно-неоднородной системы вводится две функции распределения: G1(z), описывающая профиль локальной плотности жидкости, и G12(r12 z1 z2), описывающая корреляции между частицами и частиц с поверхностью, где rij - расстояние между центрами частиц i и j, zi - расстояние от i-й частицы до поверхности. Граничным условием является переход вдали от стенки к объёмной жидкости:

  • при z1® ¥ , z2® ¥ lim G12(r12 z1 z2)= G012(r12).

Для упрощения расчётов используются два условия:

  • 1) условие термодинамического предела (постоянство концентрации): при N® ¥ , V® ¥ nv=N/V=const.

  • 2) условие синглетного приближения, когда вместо анизотропной функции G12(r12 z1 z2) используется её граничное значение для объёмной жидкости G012(r12).

В результате получается решение для функции распределения локальной плотности, параметрически зависящее от концентрации, позволяющее выразить такие макроскопические характеристики, как поверхностное натяжение и адсорбция.

Для описания структурирования воды вдоль цепи макромолекулы можно использовать статистическое рассмотрение тонких плёнок [36]. Для них условие термодинамического предела не выполняется, и плотность получается n=N/SH, где S и H - соответственно площадь поверхности и толщина плёнки. Синглетное приближение в этом случае также не работает, но вводится обобщённое синглетное приближение ( допущение о том, что твёрдые поверхности не влияют на двухчастичные корреляции в жидкости ). Используется функция G12(r12), описывающая некоторую гипотетическую объёмную жидкость с плотностью, совпадающей с плотностью плёнки. В результате получаются соотношения, позволяющие рассчитывать все структурные характеристики тонких плёнок. Соотношения дают правильные предельные переходы к объёмной жидкости вдали от стенки (H® ¥ ) и к двумерной жидкости при исчезающей толщине плёнки (H® 0).

Необходимо отметить, что локальная структура воды у цепей макромолекул сильно зависит от их формы. К тому же необходимо учитывать дипольный момент жидкости. Поэтому рассмотрение структурирования воды лишь в рамках этого описания недостаточно корректно. Работы по структурированию дипольных жидкостей вблизи поверхности и работы по структурированию с учётом формы объекта существуют, и в дальнейшем планируется применение результатов этих работ к структурированию воды у биомембран.

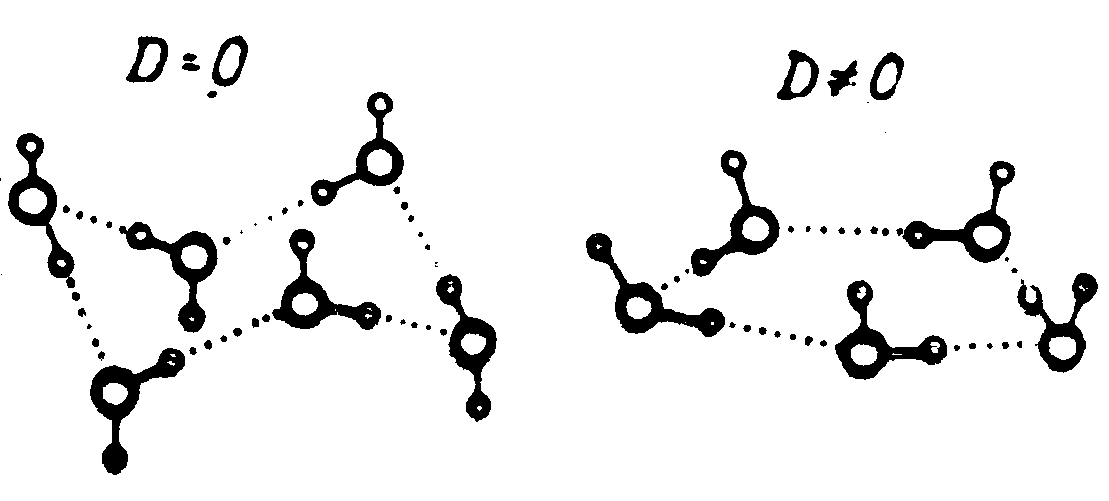
Если говорить о роли воды в процессах биорегуляции, то она обуславливает наличие в примембранной области фазовых переходов с расслаиванием [45]. Элементарные каркасы молекул воды могут быть двух принципиально различных типов - ледяные и клатратные.

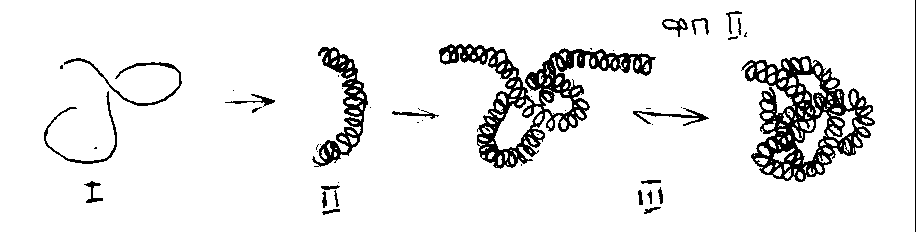
Рис. 7. Структуры белка (I) - последовательность мономеров белка (аминокислот); (II) - в данном случае a - спираль, образованная “скручиванием” аминокислотной последовательности; третичная структура (III) - пространственная конформация (линейная или глобулярная) a - спирали.

В рамках каждого из них возможно большое разнообразие конкретных форм каркасов. Это и обуславливает возможную реализацию фазовых переходов с расслаиванием. Такие переходы, происходящие в примембранной области, сопровождаются радикальным изменением структуры связей молекул воды с биомакромолекулами, то есть связаны с перестройкой ближнего порядка. Вообще, связывание воды с макромолекулами приводит к изменению конфигурации, эффективных размеров и свойств частиц. Поэтому любое варьирование структуры гидратной оболочки приводит к модификации состояния биомолекулы. Была отмечена гибкость поведения расслаивающихся растворов, высокая чувствительность их ко внешним воздействиям, а также значительное влияние некоторых веществ на устойчивость слоёв воды, связанной с биомолекулами. ( Стабилизация таких комплексов заключается в повышении температуры их разложения).

В связи с этим фазовый переход с расслаиванием было предложено рассматривать как один из механизмов передачи возмущения вдоль поверхности мембраны [45]. В случае фазового перехода с расслаиванием в системе “связанная вода - биомолекула” возможна реализация двух ситуаций. Во-первых, расслаивание в таком комплексе означает выпадение биомолекулы из раствора, то есть прекращение биохимических реакций с участием этого вещества. Во-вторых, следует учесть, что вода структурируется на поверхности биомолекулы таким образом, чтобы максимально скомпенсировать локальные заряды и дипольные моменты макромолекулы. Поэтому расслаивание означает возникновение крайне неравновесного состояния белка. При переходе к равновесному состоянию возможно локальное изменение ближайшего окружения белка, что воспримется мембраной как структурное возмущение. В дальнейшем происходит генерализация возмущения вдоль мембраны, инициирующая аналогичный конформационный переход, запускающий цепь биохимических реакций в клетке.

Таким образом, рассмотрение воды как структурированной дипольной жидкости представляется результативным в плане описания процессов биологической регуляции в клетке. При этом фазовый переход с расслаиванием может рассматриваться либо как рецепторный процесс восприятия внешнего воздействия, либо как механизм генерализации импульса, реализующийся от одного локального участка к другому в силу свойств кооперативности элементов биологической мембраны.

Лед

Клатрат

Рис. 8. Две основные формы каркасов структурированной воды

7. Сенситометрические критерии степени фотомодификации крови

Хотя к настоящему времени эффект лазерной биостимуляции кровеносной системы посредством внутривенного лазерного облучения крови (ВЛОК) твердо установлен и нашел широкое практическое применение, механизм его действия остается неясным. С одной стороны, считается, что лазерное облучение меняет конформационное состояние молекул гемоглобина, что приводит к повышению эффективности кислородного обмена в организме. Но, с другой стороны, лазерное облучение стимулирует интенсивность микрокапиллярной циркуляции крови, что не может быть объяснено только изменением состояния макромолекул, поскольку в микрокапиллярах существенными являются кооперативное взаимодействие эритроцитов и стенок сосуда (известно, что размеры эритроцита в недеформированном состоянии превышают диаметр микрокапилляра) [29].

Одной из наиболее актуальных и нерешенных проблем в области применения лазеров в медицине является дозиметрия поглощенной биотканью световой энергии и количественное определение результата лазерного воздействия, причем желательно в терминах физически измеримых величин. В настоящее время в практическом здравоохранении результаты ВЛОК определяют способом биохимического анализа крови до и после облучения, и, исходя из полученных результатов, определяют энергетический график всего курса лазерной терапии для конкретного больного. Данных такого рода опубликовано в научной литературе достаточно много, но их физическая и методическая обоснованность, хотя бы в части метрологической достоверности дозы поглощенной световой энергии, весьма сомнительны и не позволяют дать хотя бы минимального количественного описания временной динамики процесса ВЛОК. Кроме того, опубликованный массив данных очень плохо поддается интерпретации, поскольку биохимические параметры крови зависят от большого числа индивидуальных факторов, а сами методики различны у разных исследователей.

Свойства и состав крови. Кровь – особая жидкая ткань организма, в которой своеобразные клетки свободно взвешены в жидкой среде. Жидкая часть крови – плазма – имеет связь со всеми органами и тканями и отражает происходящие в них биохимические и биофизические процессы. Количество крови у человека в нормальных условиях составляет от 1/13 до 1/20 части от общей массы (3 – 5 л.). Цвет крови зависит от содержания в ней оксигемоглобина: артериальная кровь ярко-красная (богата оксигемоглобином), а венозная темно-красная (бедная оксигемоглобином). Вязкость крови в среднем в 5 раз превышает вязкость воды. Поверхностное натяжение меньше натяжения воды. В составе крови 80% - воды, 1% - неорганические вещества (натрий, хлор, кальций), 19% - органические вещества. Плазма крови содержит 90% воды, удельный вес ее составляет 1030, ниже, чем у крови (1056-1060). Кровь как коллоидная система обладает коллоидно-осматическим давлением, т. е. способна удерживать определенное количество воды. Это давление определяется дисперсностью белков, концентрацией соли и другими примесями. Нормальное коллоидно-осматическое давление составляет около 30 мм. вод. ст. (2940 Па) [50].

Форменными элементами крови являются эритроциты, лейкоциты и тромбоциты. В среднем 45% крови составляют форменные элементы, а 55% плазма. Эритроциты – безъядерные тельца и состоят из оболочки и жидкого гемоглобина, белкового вещества и нуклеопротеидов. Оболочка состоит из липоида (холестерина и лецитина). Красные кровяные тельца обладают значительной пластичностью и, по-видимому, они могут вытягиваться во время прохождения капилляров, а затем возвращаться в исходное состояние. После выхода из капилляров венозная кровь содержит большой объем кровяных телец, нежели артериальная кровь (не за счет их числа, а за счет их разбухания).Гемоглобин в норме занимает около 95% всей плотной массы эритроцита, и 13% по отношению к весу всей крови. Нормы гемоглобина меняются от условий питания, погодных условий и от мест проживания. Лейкоциты – ядерные клетки, бесцветные. Обычно лейкоцитов примерно в 800 раз меньше, чем эритроцитов. В различных частях тела число лейкоцитов разное. В расширенных сосудах их больше, чем в суженных, потому что в таких сосудах ток крови замедляется. Замечено, что лейкоциты движутся преимущественно вблизи стенок сосудов [51].

Функции крови. Кровь через стенки капилляров входит в соприкосновение с тканями организма и снабжает их кислородом, пищей, водой и даже теплом, а также уносит обратно продукты переработки, СО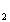, молочную кислоту и др. Красные кровяные тельца переносят газы; они воспринимают при помощи гемоглобина кислород из альвеолярного воздуха и разносят его по кровеносному руслу[50,51].

Кислород связан с гемоглобином в виде нестойкого оксигемоглобина, при прохождении через ткани гемоглобин теряет способность связывать кислород под влиянием поступающего в кровь из тканей углекислоты. Кислород покидает эритроциты, растворяется в плазме и поглощается тканями организма. Углекислота частично связывается с основаниями плазмы, частью свободно увлекается кровью в легкие и там выделяется.

Кровеносная система - это транспортная система организма, связывающая между собой все его части и снабжающая их кровью – жидкостью, выполняющей многообразные функции. Она состоит из сердца – мышечного насоса, проталкивающего кровь по множеству трубочек, называемых кровеносными сосудами. Артерии – это сосуды, по которым кровь течет от сердца к тканям и органам. Вены – сосуды, по которым кровь возвращается к сердцу. Из артерий и вен кровь протекает через тоненькие сосуды, называемые капиллярами. Свойства этих сосудов почти полностью определяются строением стенок. Артерии имеют эластичные мышечные стенки, тогда как стенки вен более дряблые и их внутренний диаметр обычно больше. Стенки капилляров очень тонкие и состоят из одного слоя клеток.

Динамика крови. В крупных кровеносных сосудах кровь можно считать ньютоновской жидкостью, то есть подчиняющийся гидродинамическим законам движения[51]. Поток крови считается ламинарным и однородным. Однако при разветвлении крупного сосуда на более тонкие могут возникать области отрыва и пограничные области, и течение становится турбулентным. Кровь с физической точки зрения представляет собой смесь жидкостей, обладающих разными коэффициентами вязкости. Коэффициент вязкости всей смеси зависит от процентного соотношения ее составляющих. С другой стороны, кровь, движущуюся по круглым каналам, может рассматриваться как суспензия – жидкость со взвешенными в ней частицами, имеющими размер гораздо меньший, чем диаметр трубы. Течение такой суспензии обладает замечательным свойством: в узкой зоне около стенок трубы взвешенные частицы отсутствуют. Это явление носит название пристеночного эффекта [52]. Физическим законам сохранения может удовлетворять движение смеси с произвольным распределением концентрации более вязкой жидкости, но, тем не менее, устанавливается такое течение, которое обладает пристеночным эффектом. При этом концентрация жидкости большей вязкости практически равна нулю у стенок трубки и максимальна в окрестности ее оси. Учет пристеночного эффекта позволяет объяснить наблюдающееся при ВЛОК снижение вязкости крови при одновременном увеличении геометрических размеров клеток крови за счет более эффективного захвата кислорода. Данное обстоятельство подтверждает необходимость облучения при ВЛОК именно сосудов- в микрокапиллярах достичь снижения вязкости крови невозможно, а это ключевой фактор при лечении, например, инфаркта миокарда.

Микрокапиллярная система. Диаметр микрокапилляров колеблется в диапазоне от 4 до 5 мкм, а их протяженность оценивается величиной около 100.000 км., поэтому они располагают огромной площадью, через которую происходит транспортный обмен веществ. В целом, капилляры образуют упорядоченную систему путей микроциркуляции, обеспечивая непрерывное движение крови около клеток организма и тканей, где осуществляются обменные механизмы, без которых жизнь тканей была бы невозможной.

При изучении капилляров [29]выяснилось, что в основе организации микрососудистой сети лежит коллективный способ функционирования капилляров и движение крови в микрососудах подчиняется иным законам, чем в макрососудах. Поэтому специфика многих биореологических феноменов, возникающих в капиллярах, определяются тем, что их размеры сопоставимы с размерами движущихся по ним клеткам крови. Это свидетельствует о необходимости анализа свойств и поведения клеток крови, находящихся в капиллярах.

Эффект аномально низкого трения при движении крови по микрокапиллярам при периодическом силовом воздействии пульсового напряжения обусловлен формированием из частиц крови т.н. волновых пакетов. В частности, этот эффект достигается за счет увеличения степени “разрыва”между структурными блоками при их движении в режиме “физического маятника”и возникновения поверхностных деформационных волн солитонного типа на поверхности клеток крови. При этом характеристики солитонных волн оказываются соразмерными рельефу шероховатости поверхностей взаимодействующих в пределах волнового пакета блоков. Пульсирующее давление способствует упаковке этих пакетов в структуры, подобные спиральному течению жидкости при входе в воронку. Поэтому можно предположить, что наличие пульсирующего воздействия, кроме непосредственного продвижения крови, является необходимым механизмом, препятствующим возникновению турбулентного движения крови по кровеносной системе[29].

Гистофизиология капилляров, предполагает, что микроциркулярное русло разделяется на относительно обособленные в структурно-функциональном плане макрососудистые блоки (или модули), что обеспечивает равные условия для доставки крови в многочисленные капилляры органа. Тем самым происходит функциональная кооперация работы капилляров не только с окружающими их тканями, но и с другими близлежащими микрососудами, определяющими режим капиллярной гемодинамики[29].

Поэтому можно предположить, что если система обеспечивает равные условия для доставки крови в многочисленные капилляры, то она может быть описана подобно полимерной макрокристаллической структуре. Структурная организация клеточных агрегатов подчиняется некоторому вероятностному принципу, в соответствии, с которым происходит минимизация потенциальной энергии структурных единиц. Поэтому реализуется принцип иерархического соподчинения, построенного на взаимодействии регулирующих систем. Между собой клетки поддерживают взаимодействие двумя способами: при помощи гормонов, действующих на расстоянии, и путем контактного воздействия, основанного главным образом на явлении клеточной поляризации[29].

Очевидно, что одну из ключевых ролей в объяснении механизма кровоснабжения организма играет понятие о границе между макро- и микроциркуляции. Стенки капилляров состоят из одного слоя клеток (так называемые источные стенки) и лишены гладкомышечных клеток. Слой устроен таким образом, что между соседними клетками есть узкие щели. Благодаря такому строению стенок капилляры обладают высокой проницаемостью для транспорта газов, воды и активного переноса веществ. Поверхность многих клеток покрыта микроворсинками. Ширина их колеблется от 50 до 100 нм., а длина от 90 до 1000 нм. Под влиянием тока крови микроворсинки совершают волнообразные движения. Они захватывают капельки плазмы, и дают начало вакуолям и микропузырькам, которые погружаются в цитоплазму. Микроворсинки значительно увеличивают общую обменную поверхность эндотелия и этим принимают активное участие в транспортировки веществ.[29]

В основе переноса веществ лежат два процесса: транскапиллярный диффузионный обмен молекулами, обусловленный разностью концентрации вещества по обе стороны стенки капилляра, и движение жидкости (конвективный перенос вещества) под влиянием сил гидростатического или онкатического давления. Скорость обмена через капиллярную стенку путем диффузии примерно в 200 раз выше, чем путем фильтрации. Газы крови и частично вода свободно диффундируют через эндотелиальные клетки, однако большая часть воды и растворенные в ней вещества проходят по межэндотелиальным щелям.[29]

Процесс обмена происходит следующим образом. За счет сокращения сердечных мышц создается давление крови, в результате этого вода с растворенными в ней питательными веществами проходит через щели. Однако размер клетки крови (размер эритроцита 8 – 10 мкм) примерно вдвое больше диаметра капилляра. Поэтому в настоящее время нет достоверных данных о механизме продвижения клеток эритроцита через микрокапилляры, но зато существует несколько гипотез о механизме передвижения клеток. Одна из таких гипотез предполагает, что эритроцит собирается в стопки, подобно монетам, и друг за другом проталкиваются через капилляры. Такой способ передвижения был назван поршневым.

Причины светочувствительности при ВЛОК. Из данных спектральных исследований известно [17], что на макромолекулярном уровне компоненты крови не имеют ярко выраженных максимумов поглощения при длинах волн излучения, применяемого для проведения ВЛОК. Поэтому, используя подход, принятый в физике полимерных голографических регистрирующих сред [53], можно предположить, что центрами светочувствительности при ВЛОК, кроме ионов железа, входящих в состав гемоглобина, могут выступать биологические макромолекулы и их ансамбли, имеющие отличный от нуля дипольный момент, т.е. имеющие сферически асимметричное конформационное состояние[42]. Последнее может быть обусловлено различными типами взаимодействия элементов крови между собой и стенками капилляров и сосудов. Можно, поэтому, сказать, что светочувствительность при ВЛОК обусловлена системными факторами и имеет фрактальную или иерархически организованную структуру как по механизм взаимодействия с когерентным излучением, так и по величинам энергетической и спектральной светочувствительности.

Предварительно можно расположить структурные элементы по убыванию значения светочувствительности (величине, обратно пропорциональной пороговой энергии стимуляции всей кровеносной системы или организма) следующим образом. В скобках указан примерный диапазон спектральной чувствительности.

  • Гидрокомплексы форменных элементов крови и стенок сосудов (КВЧ и дальний ИК диапазон [10] );

  • Коллективные модули воды и аквакомплексы белковых макромолекул (средний и ближний ИК диапазон [47] );

  • Форма оболочки эритроцитов и других элементов крови или четвертичная структура белковых макромолекул [17] (ИК и видимый спектральный диапазон);

  • Третичная и вторичная структуры белковых макромолекул типа гемоглобина [17] ( видимый спектральный диапазон);

  • Ионы железа в гемоглобине ( сине-зеленая область видимого спектрального диапазона);

  • Первичная структура белковых макромолекул (УФ спектральный диапазон).

Конечно, такое разбиение достаточно условно и вряд ли исчерпывающе, но оно соответствует принятому в биофизике разделению на типы структур белковых макромолекул [17].

Сенситометрия результатов ВЛОК. Проведя разбиение по механизмам светочувствительности кровеносной системы, логично использовать систему представления результатов взаимодействия крови с лазерным излучением в хорошо известной сенситометрической системе типа ХиД [74], широко применяемой в теории фотографического процесса. В работе [49] было проведено исследование явлений лазерной фотомодификации крови при ВЛОК способом спектрометрии образцов крови забираемой у пациентов в строго фиксированные (по отношению к лазерному воздействию) временные моменты. Использованная методика предполагает, что лечебные действия ВЛОК не связано с действием света на стенки сосуда, поскольку анализу подвергаются только образцы крови in vitro. Несмотря на такое не очень обоснованное предположение, экспериментальные данные, полученные в [49], являются, по-видимому, первыми, показывающими динамику процесса ВЛОК, как во время отдельного сеанса, так и в течение всей процедуры.

Методика получения исходных данных. Исследовался спектр поглощения цельной гепаринизированной венозной крови, взятой до и после проведения сеанса ВЛОК, технически это проводилась так: у больного, которому было назначено ВЛОК, пунктируется периферическая вена и разовым шприцом, предварительно гепаринизированным, производится забор 2-3 мл. крови, через просвет иглы в непосредственно в кровоток вводится моноволоконный световод, где кровь облучается световым конусом. Взятая венозная кровь разводится вначале на 1 мл. крови добавляется 5 мл. изотопического раствора хлористого натрия, а затем добавляется 54 мл. дистиллированной воды. Получался образец 1:60, помещают в кювету спектрофотометра "Specord" и записываются спектры поглощения в диапазоне 400-800 нм. После окончания сеанса ВЛОК производится повторный забор 2-3 мл. венозной гепаринизированной крови приготавливают разведенный образец 1:60 и проводят запись спектров поглощения.[49].

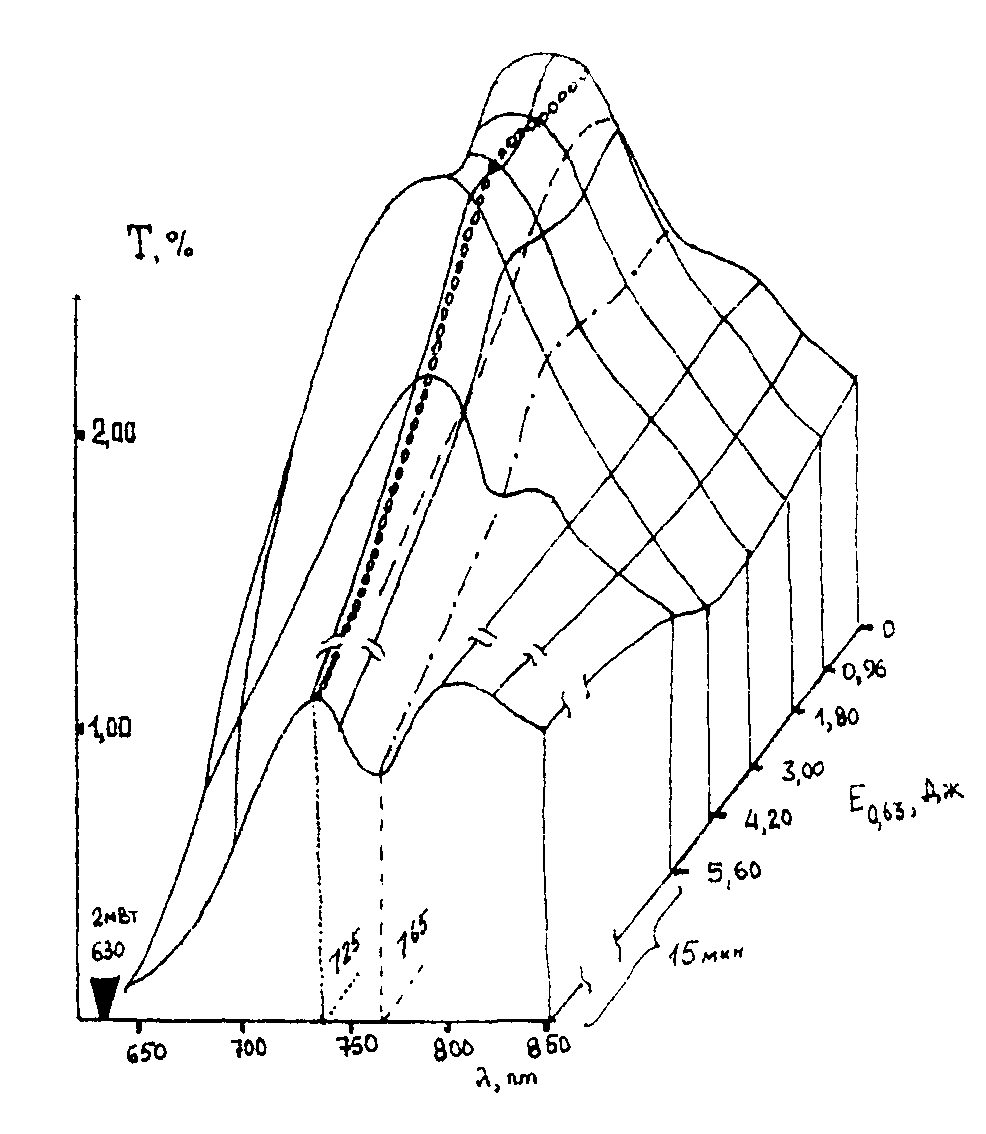
Сенситометрические поверхности. Используя данные [49] по изменению спектральных характеристик крови при ВЛОК гелий-неоновым лазером с мощностью на выходе из оптоволокна 2мВт. во время одного сеанса облучения, можно представить динамику лазерной фотомодификации крови в виде рис.9 и рис. 10. На приведенных графиках показано изменение спектрального пропускания образцов крови на разных длинах волн излучения в зависимости от энергии облучения. Энергия облучения определяется как произведение интенсивности излучения (2 мВт.) на время воздействия.

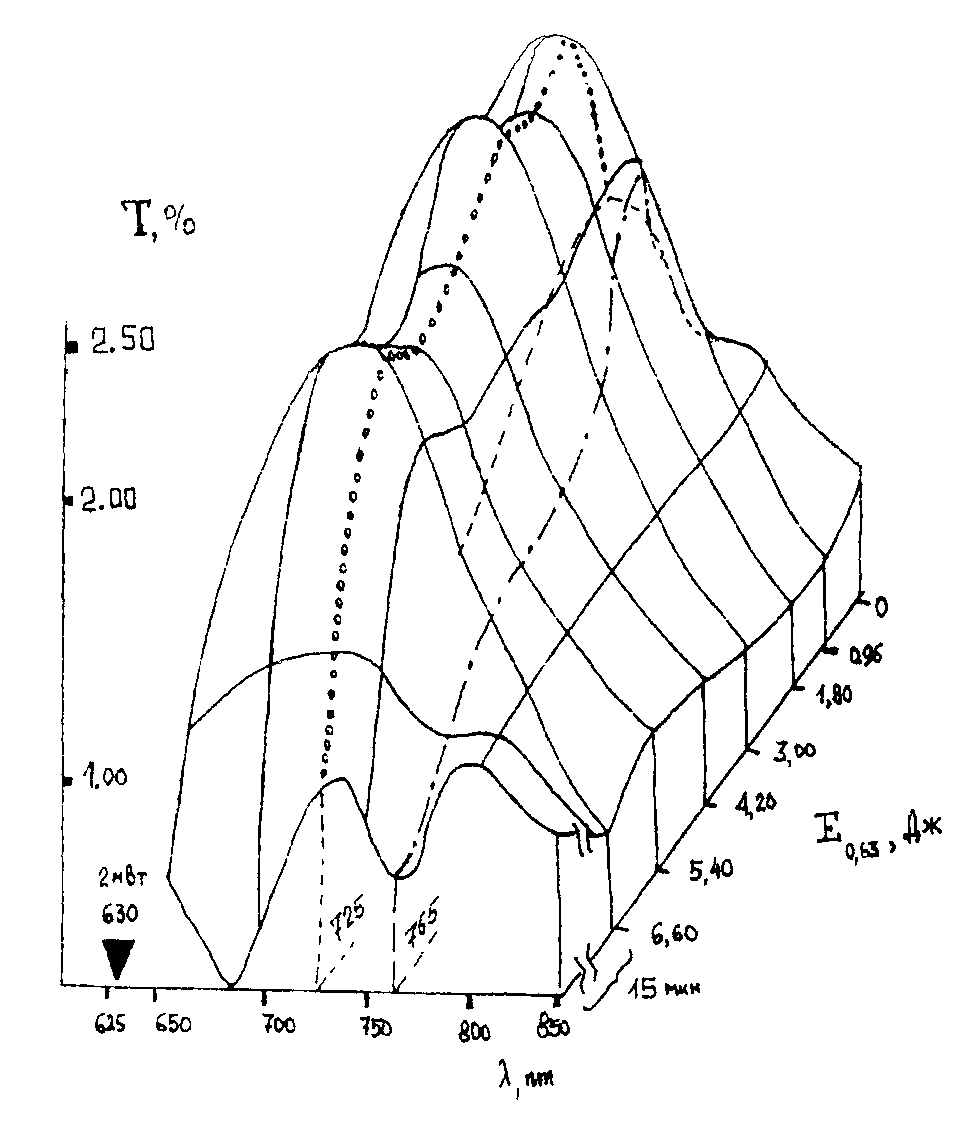
Для соматически здорового и больного пациента соответственно рис. 9 и рис. 10(а, б) величина поглощения на длине волны действующего излучения 633 нм. меняется не очень значительно. В целом можно отметить, что ВЛОК приводит к изменению функционального вида спектра пропускания крови – начальный спектр с двумя максимумами поглощения (рис.9) превращается в кривую с одним максимумом. Заметим, что на рис. 10 (а, б) до сеанса ВЛОК поверхность спектрального пропускания имеет более гладкий характер.

Учтя, что длина волны соответствует различным энергиям в спектрах поглощения крови, которые, в свою очередь, могут быть отнесены к энергиям реакции в макромолекулах крови, можно сделать следующие выводыя:

    1. фотомодификация крови лазерным излучением с l =0,63 мкм. не приводит к химическим реакциям, а ведет только к конформационным изменениям молекул;

    2. фотомодификация крови происходит по механизму фотопереноса электрона, как и в случае слоев дихромированного желатина [53]. Иными словами, квант света с l =0,63 мкм. по механизму внутреннего фотоэффекта выбивает электроны из, например, молекулы гемоглобина, что приводит к изменению зарядовой архитектуры белка всей макромолекулы. Последнее влечет за собой переноску конформационного состояния макромолекулы, что, с ростом поглощения энергии, увеличивает подвижность всей макромолекулярной цепи и облегчает, после прекращения ВЛОК, возвращение молекулы при релаксации (рис. 10(а, б)) к нативному здоровому состоянию.

    3. мониторинг процесса ВЛОК целесообразно проводить на длине волны 725 нм., где изменения поглощения наиболее ярко выражены.

Таким образом, предлагаемый новый переход к представлению данных по ВЛОК в виде сенситометрических поверхностей в координатах (Т-l -lgЕ(0,65)) позволяет интерпретировать явления лазерной фотомодификации крови как совокупность конформационных изменений макромолекул гемоглобина в результате первичной реакции фотопереноса электрона.

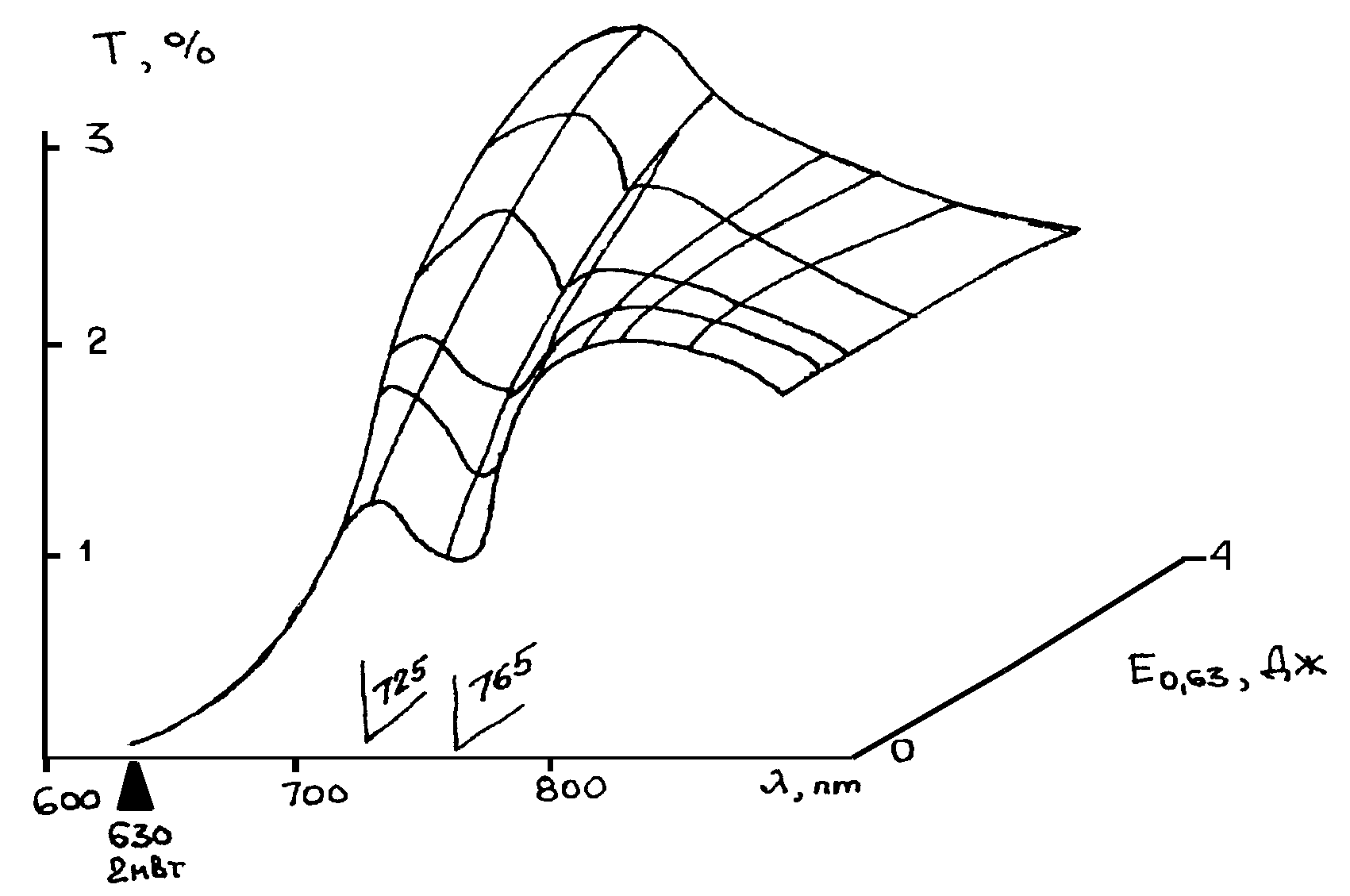
Рис.9. Изменение спектрального пропускания образцов крови на разных длинах волн излучения в зависимости от энергии облучения для здорового пациента.

а) б)

Рис. 10. Изменение спектрального пропускания образцов крови на разных длинах волн излучения в зависимости от энергии облучения. а) ишемическая болезнь сердца б) диабет.

 

8. Статистическая физика биологических процессов

Наиболее общим свойством живых систем является их неравновесность и незамкнутость по отношению к внешней среде, что обуславливает их негэнтропийность, феноменологически описывающуюся в рамках неравновесной термодинамики [5]. Основой живых организмов являются биологически функциональные вещества - биополимеры, белки и нуклеиновые кислоты, обладающие большой конформационной гибкостью. Это обеспечивает наличие широкого спектра конформационных состояний макромолекул и переходов между ними при довольно низких энергетических затратах [5, 54-56].

Теоретически биологическая макромолекула может иметь очень большое число конфигурационных пространственных состояний, не меняя своей первичной химической природы. Но находясь, например, в клетке она уже не может иметь столь широкого спектра конфигурационных состояний, что обусловлено целым рядом ограничений [15]. Во-первых, это топологические ограничения - например, должны отсутствовать самопересечения полимерной цепи, поскольку один участок цепи не может пройти через другой. Во-вторых, возникают ограничения в пространстве, связанные с наличием хотя бы границы клетки - мембраны. Поскольку in vivo данная макромолекула включена в различные биохимические и биофизические процессы, то возникают ограничения на спектр ее возможных конфигурационных состояний от соседних макромолекул и из-за взаимодействия между ее собственными полимерными звеньями. Существуют, наконец, ограничения по ресурсам для биохимических реакций в пределах клетки или организма, что приводит к возникновению значимых обратных связей во временной организации биопроцессов [57]. Эти ограничения обуславливают дискретизацию энергетического спектра макромолекулы или квантование ее состояний, чему соответствуют энергии конформационных переходов in vitro от 10 до 100 кДж/моль [3]. Сопоставляя эти величины с энергией излучения на длине волны 0,63 мкм, равной 194 кДж/моль, или на длине волны 0,87 мкм, чему соответствует 136 кДж/моль, следует сделать вывод о возможности лазерной инициации именно конформационных переходов. Реально, in vivo энергия, необходимая для конформационного перехода макромолекулы может быть еще меньше из-за наличия вышеперечисленных ограничений. Изменение конформационного состояния макромолекулы, как известно [55,56], может менять ее биологическую активность и, следовательно, ход биохимических реакций в клетке и организме.

В рамках статистико-физического подхода большая длина полимерной цепи макромолекулы приводит к возможности представления ее как облака квазимономеров [15], поскольку каждое звено находится в одинаковом, “стандартном” окружении других, в основном, ближайших полимерных звеньев. Это “стандартное” окружение приводит к перенормировке свойств (масса, заряд и т.п.) каждого звена и оно уже выступает в теории объемного взаимодействия макромолекул как самостоятельная квазичастица, характеристики которой отличаются от характеристик реального исходного звена полимера. Нахождение полимера - макромолекулы в пространственно ограниченной области, например, клетке, приводит, согласно концепции скейлинга [15,58], к возможности введения понятия блобов или доменов [17] макромолекулы, также обладающих свойствами квазичастиц (рис. 11). Физически введение понятия блоба соответствует тому, что на масштабах, меньших диаметра, например, трубки, в которую помещена макромолекула, полимерные звенья не “чувствуют” наложенного на всю цепь ограничения и этот участок остается в невозмущенном, нативном, состоянии.

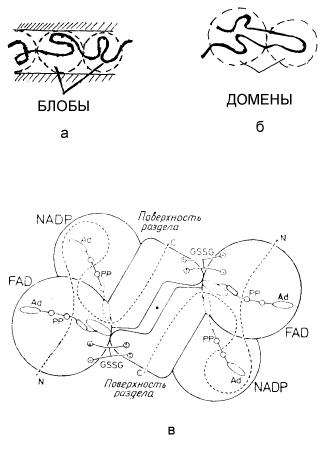
Рис. 11. Полимерная цепь макромолекулы как система блобов (а) или доменов (б) и пример доменной структуры димерного фрагмента глутатионредуктазы [17] (в). Каждая субъединица состоит из трех доменов: один из них присоединяет FAD (флавинадениндинуклеотид), другой присоединяет NADP (никотинамидадениндинуклеотидфосфат), третий образует поверхность раздела. Общий ход полипептидной цепи показан пунктирной линией. Кофакторы FAD и NADP присоединяются в вытянутых конформациях. Субстрат глутатион (GSSG) помещается между субъединицами. Каждый активный центр образован четырьмя доменами.

Изложенное показывает возможность введения в рассмотрение при анализе ЛБС понятия квазичастиц, которые по своим свойствам и характеристикам могут радикально отличаться от реальных, нативных биомакромолекул. Это обстоятельство также объясняет различие в результатах ЛБС для биообъектов in vivo и in vitro.

Конформационные состояния макромолекул также могут отличаться и структурой своего водного окружения. В физическом смысле такие системы имеют жидкокристаллическую структуру, характеризующуюся широким спектром метастабильных состояний, различающихся между собой конформациями биомакромолекул и связанных с ними гидратных оболочек. Поэтому действие лазерного излучения на биосистему связывается с фотоинициацией микроструктурных перестроек в таких жидких биосредах [3], механизм которых описывается как электронно-конформационное взаимодействие [5]. В этом случае механизм воздействия лазерного излучения можно трактовать как состоящий из первичной фотохимической реакции с переносом электрона [59] в макромолекуле с последующим конформационным изменением ассоциата, состоящего из макромолекулы и ее гидратного окружения. Другим названием комплекса таких явлений и их последствий можно считать синдром структурной альтерации биологических жидкостей, под которым понимается “трансформация структуры тканей и жидких сред организма, устойчивые структурные изменения биожидкости, проявляющиеся как локально в области воздействия лазерным излучением, так и в биожидкостях, не подвергающихся прямому облучению” [60].

В дальнейшем под конформером будем понимать определенное конформационное состояние ассоциата, состоящего из одной или нескольких биомакромолекул или их частей в сочетании с взаимосвязанными с ними молекулами воды. Отметим, что определение такого ассоциата, сохраняющего на микроуровне свойства целостного организма и являющегося в этом смысле “истиной молекулой” или “квазичастицей” всей биологической системы, является нетривиальной физической проблемой. Свойства и параметры такого ассоциата определяются, в частности, и окружением биосистемы - граничными условиями рассматриваемой задачи, что подтверждается и различием результатов экспериментов, проводимых в условиях in vivo и in vitro. Также построение общей динамической теории эффекта ЛБС усложняется возможностью взаимопревращения различных типов квазичастиц - конформеров и превращения их в солитоны, экситоны, поляроны и др. квазичастицы. Тем не менее, используя результаты статистической теории открытых систем [14], можно дать общее описание процесса ЛБС.

Как уже отмечалось, матричность и стереохимичность биохимических реакций требует наличия механизма “селекции” нужных конформационных состояний молекул, который можно рассматривать как механизм формирования инверсии населенности энергетических уровней и как аналог системы накачки в лазерах. Заметим, что формально-теоретическое сходство живых организмов с другой открытой, но квантово-радиофизической системой - лазером - отмечалось в [61]. Дефектность или “заболевание” клетки приводит к падению эффективности такой “накачки” до значений, меньших определенного порогового уровня, что может быть описано как термолизация - переход молекул к равновесному тепловому Больцмановскому распределению по энергетическим состояниям. Если использовать для описания инверсных состояний понятие отрицательной эффективной температуры [62], то можно сказать, что “заболевание” клетки соответствует переходу от “высоких отрицательных значений” температуры до “низких” тепловых температур, которые уже описываются стандартной статистической физикой равновесных систем.

Непригодность статистической теории равновесных систем для описания биосистем связана с тем, что в равновесном ансамбле Гиббса число контролируемых степеней свободы очень мало и поэтому велика неопределенность задания микросостояний отдельных систем ансамбля. Т.е. в классическом описании изначально заложена высокая степень хаотичности или, иными словами, некогерентности состояний элементарных подсистем. А в случае биосистем наличие обратных связей приводит к тому, что стационарное состояние системы отличается от равновесного и квазичастицы - конформеры находятся в когерентном состоянии, что и обеспечивает появление кооперативных эффектов. В этом смысле можно сказать, что ситуация в биосистемах подобна, хотя бы формально-математически, другим известным в физике кооперативным явлениям - сверхтекучести и сверхпроводимости. Именно когерентность ансамбля конформеров - согласованность их волновых функций - обеспечивает функционирование живых систем, т.е. можно сказать, что биовещество является когерентным веществом [12]. Важным обстоятельством, кроме открытости биосистемы, является и ее активность: отдельными элементами являются малые активные объекты.

Базовым уравнением статистической теории активных сред - теории самоорганизации - синергетики, является уравнение реакционно-диффузного типа

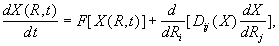(11)

носящее название уравнения Фишера-Колмогорова-Петровского-Пискунова (ФКПП) [14]. В этом уравнении X(R,t) - некоторая совокупность (вектор) характеристик системы типа концентраций, поля скоростей и т.п.; R - пространственная координата, t - время. Нелинейные функции F определяются структурой элементов системы, а величины Dij определяются коэффициентом пространственной диффузии элементов системы. Реальное применение (11) для описания систем типа биологической клетки весьма и весьма ограничено даже при использовании компьютерных методов из-за сложности хотя бы ее пространственной структуры. Можно отметить сходство этой задачи с задачей восстановления характеристик шероховатой поверхности в оптической бесконтактной диагностике [63], где вместо детального описания геометрии рельефа используют статистические параметры, а при экспериментальном исследовании применяют корреляционный анализ.

Согласно [14] первостепенной задачей является конкретизация понятия элемента открытой активной системы, в качестве каковых могут выступать и обсужденные выше конформеры. Поэтому для описания биосистем и процесса ЛБС необходимо, видимо, перейти на более высокий уровень - использовать кинетическое уравнение для функции распределения f(X,R,t) конформеров по энергетическим состояниям.

В связи с тем, что любая биосистема есть упорядоченная система, в качестве основного параметра следует использовать характеристику упорядоченности - энтропию. Следуя [14], можно выделить следующие преимущества энтропийного состояния: энтропия может быть определена для произвольного неравновесного состояния, если известна соответствующая функция распределения. Последняя может быть определена как методом математического моделирования, так и непосредственно из экспериментальных данных типа временных реализаций, спектров, пространственных распределений.

В соответствии с [14, стр.43], если система характеризуется произвольной функцией Гамильтона Н(Х) и в равновесном состоянии распределение состояний конформеров 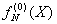определяется каноническим распределением Гиббса, то по теореме Гиббса энтропия равновесного состояния больше энтропии произвольного состояния при условии, что его средняя энергия равна средней энергии равновесного состояния. В случае биосистемы условие равенства средних энергий

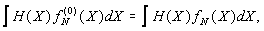(12)

где fN(X) - функция распределения конформеров для неравновесного состояния, выполняется, поскольку из соображений минимизации теплопотерь средняя энергия элементов биосистемы равна средней тепловой энергии элементов окружающей среды или близка к последней. Поэтому, поскольку условия теоремы Гиббса выполняются, для разности энтропий равновесного S(0) и неравновесного S(T) состояний имеет место неравенство

Рис. 12. Изменение статистических функций распределения биосистемы и когерентного поля при лазерной биостимуляции.

а - до взаимодействия систем;

б - после взаимодействия систем;

в - “обмен” состояниями когерентности между фотонным и конформерным ансамблями.

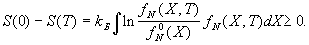(13)

Можно сказать, что из теоремы Гиббса следует ограничение на вид функции распределения конформеров в соответствии с уравнением (12).

Пусть до воздействия лазерного излучения энтропия системы “ансамбль клеток + свет” была равна:

S(0) = S0(1) + S0(2) + S0(3), (14)

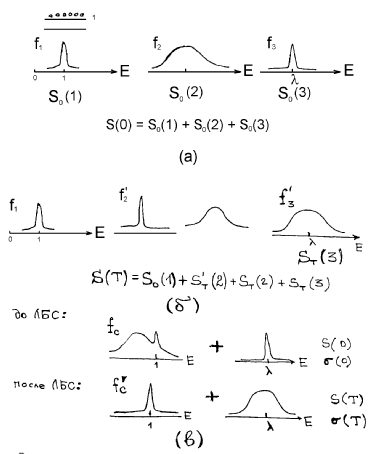
где S0(1) - энтропия “здоровых” клеток, S0(2) - энтропия “больных” клеток и S0(3) - энтропия когерентного электромагнитного поля. В соответствии с физическим смыслом энтропии S0(2) соответствует гиббсовское распределение с температурой биосистемы (близкой для минимизации теплопотерь к температуре окружающей среды), а энтропиям S0(1) и S0(3) соответствуют неравновесные распределения, поскольку эти системы являются когерентными (рис. 12а). После лазерного облучения количество “больных” клеток уменьшается, а когерентность излучения падает и его распределение из-за рассеяния (упругого и неупругого) в процессе взаимодействия эволюционируют к тепловому виду(рис. 12б). В соответствии с теоремой Гиббса (13) и принципом Пригожина, показывающим, что при неравновесных фазовых переходах, формирующих процесс самоорганизации, система идет по пути минимизации производства энтропии s = dS/dT в стационарном состоянии; для состояния “0” до момента ЛБС и состояния “Т” после окончания облучения имеют место неравенства:

S(0) - S(T) ³ 0

(15)

s (0) - s (T) ³ 0.

В терминах функций распределения конформеров процесс ЛБС описывается в тех же обозначениях, что и в [14], но под функцией распределения следует понимать функцию распределения конформеров и электромагнитного поля (рис. 12в). Тогда уравнения (12) и (15) можно рассматривать как ограничение на класс “произвольных” распределений конформеров.

Таким образом, эффект ЛБС можно трактовать как своеобразный “обмен” когерентными свойствами между биовеществом и электромагнитным полем: в результате взаимодействия лазерный свет рассеивается и поглощается, а неравновесная декоррелированная биосистема возвращается в полностью когерентное состояние. Общие физические механизмы причин такой самоорганизации были рассмотрены выше. Процесс ЛБС можно также интерпретировать и как своеобразный “теплообмен” между двумя системами, имеющими отрицательную абсолютную температуру - биосистемой и когерентным электромагнитным полем.

С экспериментальной точки зрения при определении относительной степени упорядоченности - энтропии - открытых систем вместо временных реализаций удобно использовать временные спектры электрических параметров биообъектов либо спектры рассеяния зондирующего объект излучения до и после лазерного облучения [14]. Конечно, выбор типа зондирующего сигнала для исследования эффекта ЛБС представляет собой серьезную научную проблему. Определенные возможности по моделированию эффекта ЛБС открывают исследования биоподобных самопроявляющихся регистрирующих сред на основе желатин-глицериновых композиций, которые светочувствительны к синему излучению, а в качестве зондирующего может использоваться излучение гелий-неонового лазера. Для описания работы подобных сред использовалась концепция конформеров [64,65], а перспективность использования желатиновых голографических регистрирующих сред как биоподобных моделей живых систем впервые обсуждалась в [9].

9. Нелинейная динамика при ЛБС

Биологическая система, в частности клетка, представляет собой нелинейную динамическую систему и поэтому может быть описана в рамках нелинейной динамики [66-68]. В нативной или “здоровой” клетке ее динамика соответствует стационарному состоянию, характеризуемом множеством значений переменных х, при котором состояние системы не меняется со временем. В самом общем виде в рамках базовой модели нелинейной динамики - одномерного отображения [66] - можно записать

xn+1 = f(xn,a ), (16)

где xn - соответствует набору переменных состояния в момент времени tn, f - непрерывная функция, описывающая, например, биохимические процессы в клетке, и a -обобщенный параметр, описывающий как саму систему, так и окружающую среду и взаимодействие между ними. Поскольку эволюция поведения системы существенно зависит от параметра a , то его иногда называют управляющим параметром.

Стационарное во времени “здоровое” состояние клетки соответствует неподвижной точке x* отображения:

x* = f(x*, a ), (17)

что показывает отсутствие зависимости динамических процессов от начала временного отсчета tn. Для функций f достаточно общего вида [66], соответствующих реакциям диффузно-химического типа, при изменении параметра a динамика поведения системы меняется по так называемому сценарию М. Фейгенбаума - происходит переход к хаосу в результате бесконечного каскада бифуркаций удвоения периода [66,67]. В общепринятом варианте бифуркационная диаграмма [66], показывающая распределение значений неподвижных точек от параметра a , приведена на рис. 13а. В соответствии с вышеприведенными соображениями под управляющим параметром a , (см. уравнение (8)) следует понимать энергию дипольного (3) и/или мультипольного момента макромолекулы в собственном поле клетки .

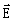На рис. 13б показана схема происхождения видов по Ч. Дарвину, заимствованная из [5]. Очевидное сходство этих диаграмм наводит на мысль, что в качестве управляющего параметра в эволюционном развитии выступает ресурс окружающей среды, вовлекаемый всеми популяциями в оборот для обеспечения своей жизнедеятельности. Нет оснований предполагать, что динамический сценарий развития мельчайших биосистем типа клеток и биомакромолекул радикально отличается от процесса филогенеза.

 

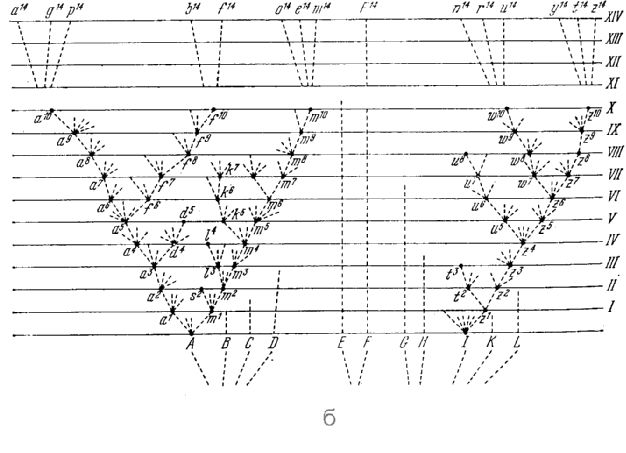
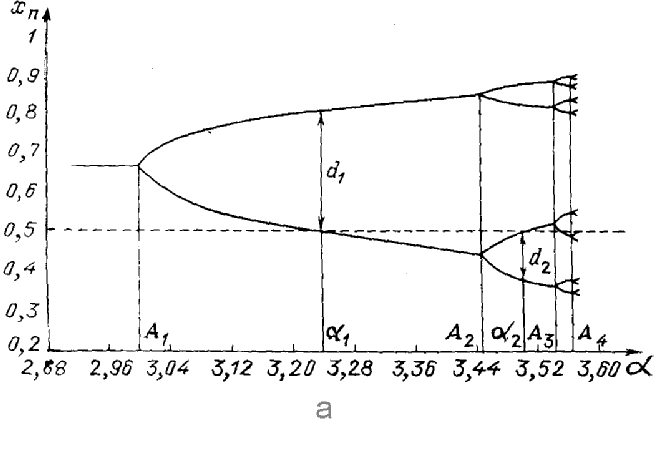
Рис. 13. Переход к хаосу в результате каскада бифуркаций удвоения периода в нелинейной динамической системе. а - диаграмма М. Фейгенбаума для неподвижных точек отображения f(x) = l x(1-x) [66]. б - схема происхождения видов по Ч. Дарвину. A,B,...L - виды обширного рода. Пунктирные линии, выходящие из А и I, - изменяющиеся потомки этих видов. Промежутки между горизонтальными линиями отвечают 1000 или большему числу поколений, а1, m1 и т.д. - ясно обозначившиеся разновидности, a10, f10, m10 и т.д. - новые виды, F14 - вид, сохранившийся без изменений [5].

 

Если считать, что нормальное функционирование некой биомакромолекулы соответствует управляющему параметру a <A1 (рис. 13а), а нарушение ее функционирования ведет к увеличению дипольного момента 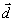или поля 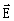внутри клетки, как обсуждалось выше, что обуславливает рост параметра a , что, в свою очередь, соответствует бифуркации удвоения периода. Если рассматривать ансамбль “больных” клеток, то подобная их эволюция ведет к хаотизации ансамбля (правый край диаграммы рис. 13а) и соответствует с физической точки зрения термолизации этого ансамбля (переходу из когерентного состояния вещества в равновесное, тепловое состояние), а с биологической точки зрения описывается как процесс гибели клетки и ее устранения процессами фагоцитоза. В рамках модели ферментативного катализа [23] это наглядно можно представить как “приобретение” “ключом” или “рукой” таких энергий, что они разрушают структуру “замка” или “перчатки” при попытке сближения, т.е. комплементарное сближение реагентов становится невозможным, а излишняя энергия выделяется в виде тепла.

При наличие в биосистеме электромагнитного поля лазерного излучения также происходит возрастание управляющего параметра a , но уже за счет величины 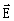в уравнении (8). Большее значение дипольного момента у “больных” биомакромолекул (клеток) приводит к ускорению движения их к хаотическому состоянию и гибели, а в “здоровых” клетках, как обсуждалось выше, в первую очередь ускоряются процессы синтеза, а именно тех их звеньев, где имеются относительно большие дипольные моменты у реагентов. Если интенсивность электромагнитного поля такова, что параметр a для одной из стадий синтеза превышает величину А1, то это проявляется как процесс угнетения биологических процессов, а не стимуляции. Оценка критической максимальной величины электрического поля 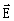, вызывающего выход за пределы действенности механизма обратной биологической связи (a £ А1), может, по-видимому, быть сделана по степени максимального нагрева клетки, происходящего под действием лазерного излучения [69].

Конкретизация предложенной концепции описания эффекта ЛБС в теоретическом плане представляется достаточно сложной проблемой. Это, во-первых, связано со сложностью описания процессов взаимодействия биомакромолекул в определенном конформационном состоянии с электромагнитным полем, зависящем и от анализируемой молекулы и от граничных условий, связанных как со структурой клетки, так и с цитоплазматическим веществом. Как минимум, подобные модели требуют использования аппарата тензорного анализа, а при попытке учета динамики изменения самого конформационного состояния макромолекулы, задача, очевидно, переходит в разряд трансвычислительных. Поэтому целесообразно экспериментально определять величину А1 для управляющего параметра как дозу поглощенного лазерного излучения, угнетающую биологические процессы. Можно предположить, что неоднозначность экспериментальных данных по пороговым значениям интенсивности лазерного излучения для ЛБС связана со сложной (в математическом смысле) структурой управляющего параметра a .

10. Модовая концепция для описания эффекта ЛБС

Актуальной является задача разработки адекватной оптической трактовки процессов взаимодействия лазерного излучения с биологическим веществом и, в особенности, мало исследованного механизма структурирования волнового поля в биоткани, подготавливающего физические условия собственно фотохимической реакции. Очевидно также, что математическое моделирование эффекта ЛБС сможет дать необходимые рекомендации по постановке экспериментов, расчету и прогнозу различных аспектов медицинского применения лазеров.

В этом направлении существенные результаты по определению пространственного распределения световой энергии внутри биологических структур получены на основе теории переноса излучения, многопотоковой теории, диффузного приближения и при использовании метода статистического моделирования (метода Монте-Карло) [70,71]. С оптической точки зрения подобные методы являются различными модификациями закона Бугера и, позволяя рассчитать распределение интенсивности в толщине биоткани, не дают информации о тонкой структуре светового поля ткани, обусловленной как микроструктурой клетки, так и степенью когерентности излучения. Усредненные значения распределения интенсивности когерентного излучения по глубине биоткани не могут служить основой для объяснения таких, явно связанных именно с пространственной структурной неоднородностью воздействующего светового поля, эффектов как повышение кровотока и активация транспорта веществ через сосудистую стенку [3]. Из общих соображений следует, что первопричиной таких проявлений биостимуляции лазерным непрерывным излучением может служить только регулярная пространственная неоднородность светового воздействия. Возникновение же такой регулярной неоднородности можно, в свою очередь, объяснить только влиянием клеточной структуры биоткани, а именно, дифракцией на ней когерентного излучения. С другой стороны, из теории фотографического процесса и исследований в области регистрирующих сред для голографии [72-74] известно, что эффективность протекания первичной фотохимической реакции существенно зависит от пространственной структуры экспонирующего освещения. В случае лазерной биостимуляции подобная зависимость должна оказаться более сильной, поскольку диффузные процессы в биотканях имеют более интенсивный характер, чем в фотоэмульсиях.

Особенности структуры поля при дифракции светового когерентного излучения на клеточных структурах можно определить в рамках традиционного квазиоптического подхода [75,76] без учета случайной составляющей рассеяния, приводящей к образованию спекл-структур и в среднем описывающейся статистическими методами [70,71].

При взаимодействии лазерного излучения инфракрасного и видимого диапазона с биологическими клеточными структурами, имеющими характерный размер регулярной неоднородности - линейный размер клетки - d от 100 до 1 мкм, можно выделить, как и в теории дифракции, две характерные области: квазиоптическую (d> > l ) и резонансную (d~ l ). В резонансной области существенную роль играют так называемые собственные электромагнитные колебания, возбуждаемые в объеме неоднородности (клетке) падающей волной [77]. Поскольку каждому конечному физическому телу присущ свой дискретный набор собственных колебаний (мод), то основной вклад в рассеянное поле, распространяющееся далее в глубь биоткани, дает излучение той колебательной моды клетки, частота, поляризация и пространственная форма которой ближе к таковым для падающей волны. Учитывая, что система клеток многослойна, можно сделать вывод, что после прохождения через достаточно большое число слоев асимптотически установится распределение интенсивности изучения, соответствующее “усредненным” параметрам клетки. Иными словами, можно сказать, что имеются резонансные условия для прохождения монохроматического излучения через клеточную структуру. Этот процесс можно трактовать и как “самоподстройку” характеристик падающего излучения под оптические свойства системы, поскольку наибольшее пропускание имеет место для пространственно-временных мод, содержащихся в падающей волне и соответствующих наинизшей моде элементарной составляющей структуры - клетке.

В квазиоптической области (d> > l ) основное влияние оказывают локальные неоднородности структуры, т.е. границы клеток. При этом считается, что относительный вклад мод колебаний отдельной неоднородности достаточно мал. В этом случае дифракционные явления в окрестностях каустик, фокусов и в зоне полутени учитываются как эффект диффузии лучевой амплитуды в смежные лучевые трубки, т.е. по волновым фронтам распространяющегося излучения [76-78], и описываются параболическим уравнением Леонтовича.

Клеточная структура представляет собой периодическую квазиоптическую систему, состоящую из повторяющихся структурных элементов - клеток, и поэтому поперечная структура волнового фронта излучения в силу симметрии должна также повторяться через тот же период d, что можно записать в виде условий теоремы Флоке [75]:

u(x,y,z+d) = u(x,y,z)e-jj (18)

где u(x,y,z) - амплитуда когерентного поля, j - фазовый сдвиг, приобретаемый волновым фронтом при прохождении одного слоя толщиной d, j= 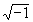. Хорошо известно [75,76], что распространение излучения в периодических структурах типа “линзовых” или “диафрагменных” линий (являющихся физическими аналогами открытых лазерных резонаторов) описывается однородным интегральным уравнением Фредгольма второго рода

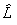{u}=m u , (19)

где 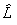- интегральный оператор, имеющий, например, в случае “линзовой” линии вид:

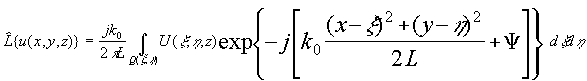,(20)

где 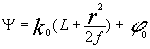; Q(x ,h ) - область интегрирования, определяемая апертурой единичной линзы, j o - фаза поля в плоскости Qo, f -фокусное расстояние линзы, ko=2p /l - волновое число, а остальные обозначения приведены на рис. 7, где показана схема только одного каскада “линзовой” линии.

 

Уравнение (19) имеет счетное множество собственных значений {m n} и соответствующую им совокупность собственных функций {Un(x,y)}, которые в теории резонаторов называют модами. Собственное значение m i, которое может быть и комплексным, определяет энергетические потери величиной (1-|m i|2) из-за попадания части излучения за пределы линзы и набег фазы на arg m i при прохождении волнового фронта от одной линзы до другой [75,76].

 

 

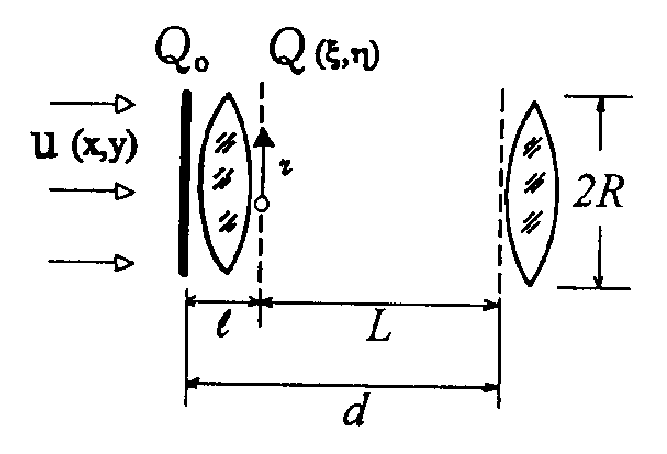
Рис. 14. Параметры элементарной ячейки клеточной структуры.

 

 

Рис. 15. Схема структуры установившегося волнового фронта в клеточной структуре.

 

 

 

 

В достаточно протяженной линзовой линии устанавливается собственная волна с минимальными потерями (1-|m o|2) и модой - распределением амплитуд - uo(x,y), которой соответствует наиболее узкий пучок, идущий вдоль оптической оси системы. В том случае, когда не выполняется неравенство R2>>l d, каждая последующая линза не сможет “перехватить” идущий от предыдущей линзы световой поток энергии и передача излучения будет сопровождаться большими радиационными потерями - выходом излучения за пределы линзовой линии. Понятно, что в этом случае, поскольку R~d, то и d~l , и ситуация будет соответствовать резонансной области дифракции, обсужденной выше.

Поскольку в уравнение (19) как параметр входит и длина волны излучения l , то проведенное рассмотрение относится к монохроматическому излучению. Другими словами, взаимодействие монохроматического излучения с клеточной структурой имеет резонансный по l характер, поскольку установившаяся мода uo(x,y) зависит от l как параметра. В реальных биологических структурах мода uo(x,y), если облучение проводится плоским волновым фронтом, формируется первым по ходу излучения слоем клеток из-за сильной оптической неоднородности последних. Очевидно, что оптимальным в смысле максимизации световой энергии, попадающей вглубь клеточной структуры, является освещение первого слоя клеток коллимированым вдоль оптической оси линзовой линии когерентным излучением с плоским волновым фронтом. Учитывая, что в реальной медицинской практике все облучаемые органы имеют кривую поверхность, следует признать целесообразным введение в состав лазерных терапевтических приборов адаптивных оптических элементов, осуществляющих фазовую коррекцию падающего волнового фронта, согласованную с кривизной облучаемого участка.

Модовый характер распространения излучения в линзовой или диафрагменной линии формально аналогичен модам световода, используемым в волоконной оптике. Поскольку периодические оптические и, в частности, клеточные системы можно рассматривать как волноводную среду с характерным квантованием значений постоянной распространения по всем трем координатным осям, то можно определить моды как устойчивые при распространении в такой среде волновые поля [79]. Моды не расплываются и не изменяют пространственной структуры в процессе распространения в своей среде, а лишь приобретают фазовый набег, пропорциональный пройденному расстоянию согласно уравнениям (19) и (20).

После того, как излучение прошло несколько слоев клеток и режим принял установившийся характер [80], устойчивость моды uo(x,y) имеет место при любом пройденном излучением расстоянии. Поэтому если облучается площадь размером (2M+1)(2N+1) клеток, где M,N >>1, то весь установившийся волновой фронт (рис. 15) можно описать выражением:

uc(x,y) = 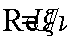uo(x-md,y-nd), (21)

где элементарная мода uo(x,y) определяется как собственная функция уравнения (19) если d>>l , либо как распределение поля, соответствующее моде собственных колебаний отдельной клетки при d~l .

Чтобы, независимо от предположений о характере первичной фотохимической реакции, происходила биостимуляция живой ткани лазерным излучением необходимо, чтобы тонкая пространственная структура последнего соответствовала всей клеточной структуре. В силу резонансного характера взаимодействия излучения с клеточной структурой, как показано выше, необходимо, чтобы пространственная структура рассеянного поля имела максимальный контраст, что достигается при высокой монохроматичности и пространственной когерентности падающего излучения [81].

Для обеспечения максимального согласования всего поля, состоящего из элементарных мод, с облучаемой биоструктурой, которое осуществляется за счет селекции мод в клеточных линзовых или диафрагменных линиях, желательно проводить одновременное облучение всего массива (2M+1)(2N+1) клеток. Действительно, если облучать клеточную структуру сканирующим лазерным лучом, то распределение интенсивности вместо квадрата модуля выражения (21), примет вид:

IS(x,y)=|uS(x,y)|2 = 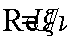| uo(x-md,y-nd)|2 (22)

и биостимуляция каждой клетки происходит независимо от других, хотя по смыслу биологических явлений все клетки функционируют согласовано. В случае одновременного когерентного освещения всего массива (2M+1)(2N+1) клеток распределение интенсивности записывается в виде:

Ic(x,y)=|uc(x,y)| = | uo(x-md,y-nd)|2 (23)

и содержит в правой части интерференционные слагаемые, что делает поле (23) более структурно разнообразным и топологически связанным по сравнению с полем (22).

Если использовать для оценки сложности структуры когерентного поля концепцию теории степеней свободы оптического изображения [82], где под общим числом степеней свободы поля излучения понимается количество действительных величин, необходимых для его полного описания, то видно, что для описания поля (22) необходимо (2M+1)(2N+1) действительных величин, а для поля (23) - вдвое больше из-за комплексного характера членов ряда, находящегося целиком под знаком модуля.

Из общей теории управления сложными системами [83] следует, что для обеспечения информационного воздействия на них необходимо достаточное разнообразие внешнего сигнала (принцип необходимого разнообразия У. Р. Эшби), которым в данном случае является установившееся в клеточной биоструктуре поле. Степень разнообразия может быть оценена количеством Шенноновской информации, содержащейся в воздействующем сигнале, которое, в свою очередь, определяется общим числом степеней свободы оптического поля [82]. Поэтому, воздействие на биосистему несканирующего полевого облучения в информационном смысле более эффективно для биостимуляции, чем поточечное сканирование, если не принимать во внимание энергетические соображения. Кроме этого, как и в случае когерентных изображающих систем, распределение степеней свободы волнового поля при несканирующем облучении имеет пороговый характер, а не ниспадающий как в сканирующем режиме, аналогичном некогерентным изображающим системам [82]. Следует, тем не менее, заметить, что ситуация со сканирующим режимом биостимуляции, если учитывать временные изменения реальной биосистемы, может оказаться довольно сложной. Поэтому при выборе параметров сканирования следует учитывать как периоды собственных колебаний и движений клеток и всей структуры, так и времена диффузии продуктов первичной фотохимической реакции. В принципе, конечно, режим сканирования будет идентичен непрерывному облучению, если время развертки луча гораздо меньше минимального времени, характерного для биологических процессов.

Таким образом, квазиоптический подход к дифракции когерентного излучения на клеточных структурах показал, что взаимодействие носит существенно резонансный характер по отношению к спектральному составу света в том смысле, что максимально пространственно неоднородное и структурно разнообразное распределение интенсивности излучения в биоткани возникает при монохроматическом освещении, имеющем высокую пространственную когерентность. В связи с этим представляет значительный интерес медицинское сравнительное исследование процессов ЛБС в тканях с размерами клетки около 5 мкм излучением гелий-неонового лазера (когда d>>l , т.е. имеет место квазиоптическая область дифракции) и излучением СО2-лазера с длиной волны 10,6 мкм (когда d~l , т.е. имеет место резонансная область дифракции). Сопоставление подобных экспериментальных данных могло бы способствовать прояснению механизма взаимодействия лазерного излучения с биологическим веществом.

Периодичность биотканей по трем пространственным координатам приводит и к возникновению продольной периодичности светового поля из-за наличия периодических структурных изменений поля в плоскости, перпендикулярной направлению распространения. В традиционной оптике подобные процессы известны как явления саморепродукции или самоизображения структуры светового поля и классифицируются как эффекты Лауэ (для некогерентного освещения) и эффект Тальбота (для когерентного освещения) [84]. Малая интенсивность некогерентных источников света позволяет не учитывать эффект Лауэ при анализе процессов распространения света в биотканях и ограничиваться феноменологическим описанием в рамках закона Бугера. Иначе обстоит дело в случае лазерных источников света, обеспечивающих высокую интенсивность монохроматического пространственно когерентного освещения, когда поперечная периодичность поля излучения вызывает периодичность поля в продольном направлении. При анализе эффекта Тальбота в оптике [84-86] обычно рассматривают объекты типа одной или нескольких дифракционных решеток. В случае биоткани, очевидно, возникает более сложная, требующая дальнейших исследований, задача распространения световой когерентной волны в существенно периодической по трем измерениям среде. Тем не менее, результаты теоретических и экспериментальных исследований процессов дифракции когерентного излучения на периодических структурах для целей мультипликации изображений [85] и в бесконтактной метрологии [86] могут быть использованы в качестве исходных данных для уяснения примерной структуры светового поля в биосистемах.

Для волнового уравнения

Ñ 2U + k2U = 0 (24)

где k = 2p /l , l - длина волны, U(x,y,z) - трехмерная функция волнового поля. Если поле U(x,y,z) обладает свойством самоизображаться вдоль оси z, то оно периодично вдоль направления распространения - оси z - с периодом D z и его можно представить в виде ряда Фурье

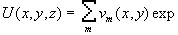(j2p mz/D z) (25)

c граничным условием

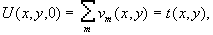(26)

где t(x,y) - амплитудное пропускание предмета. Если такое волновое поле U(x,y,z) соответствует волновому уравнению, то должны выполняться дифференциальные соотношения

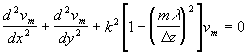. (27)

Для определения требований к объекту, формирующему свои самоизображения [84], рассмотрим случай

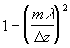>0

или (28)

D z/l >m³ 1.

Используя Фурье-преобразование:

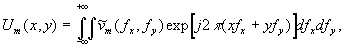(29)

где 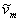- означает фурье-образ функции vm, представим дифференциальное уравнение для vm(x,y) в пространственно-частотной области в виде:

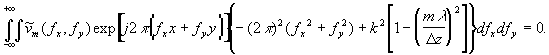(30)

Последнее уравнение выполняется, если 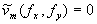или если выражение в фигурных скобках равно нулю. Поэтому достаточным условием для саморепродукции поперечной структуры оптического поля вдоль направления его распространения является наличие у периодического предмета спектра пространственных частот, соответствующих условию Монтгомери [84] (рис. 16):

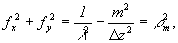(31)

где m - ограниченное целое, 0£ m£ mmax£ D z/l (величина mmax определяется условием появления затухающих волн), fx , fy - пространственные частоты спектра периодического предмета с периодом dx и dy, fx=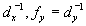), l - длина волны излучения. Если предметом является дифракционная решетка с периодом d, то плоскости точного самоизображения - плоскости изображения Тальбота - находятся на расстояниях, кратных величине [86]

D z=2d2/l (32)

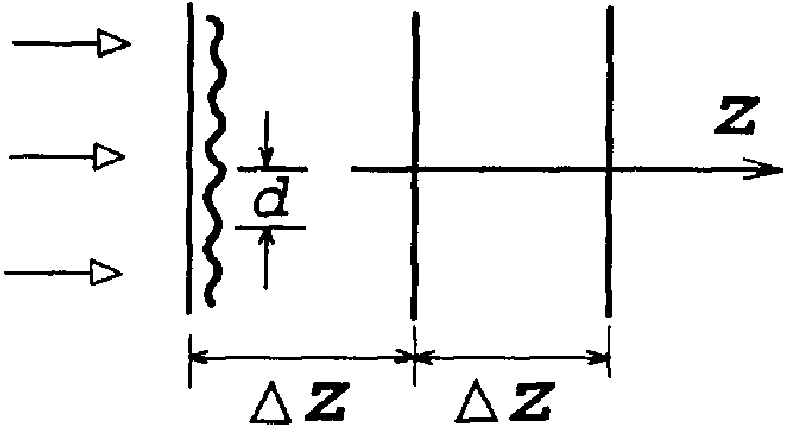
от плоскости периодического предмета. На полпути между этими плоскостями интенсивность света также воспроизводит первоначальное изображение, но сдвинутое по поперечной координате на полпериода.

 

 

 

Рис. 16. Расположение плоскостей самоизображения - плоскостей Тальбота - для периодического предмета.

 

 

 

Поскольку такой сдвиг в большинстве случаев несущественен, то можно считать, что изображения Тальбота наблюдаются на эквидистантных расстояниях

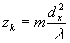(33)

от плоскости предмета. Явление саморепродукции связано с интерференцией когерентных волн, дифрагировавших на предмете и поэтому число реально наблюдаемых плоскостей Тальбота существенно зависит от размера апертуры и, как экспериментально установлено, необходимо наличие в пределах апертуры предмета минимум 17-25 периодических изменений [84].

Если предмет имеет комплексное амплитудное пропускание (в одномерном случае):

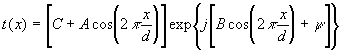(34)

то, согласно [84],

(1) в плоскостях, определяемых уравнением (33), интенсивность света соответствует изображению в плоскости z=0, причем наблюдается изображение поглощающей части комплексного пропускания и нет плоскостей, где наблюдается изображение только фазовой части;

(2) местоположение плоскости наилучшего по контрасту изображения зависит от исходного контраста А/С и величины фазовой модуляции В;

(3) поведение распределения интенсивности в плоскостях Тальбота при фазовой модуляции В>p /4 в основном определяется фазовой составляющей комплексного пропускания.

Следует отметить, что аналитически провести анализ явления самоизображения в полном объеме практически невозможно и поэтому используют, как правило, методы компьютерного моделирования. Это относится, в частности, и к рассмотрению самоизображения в непараксимальном приближении при больших углах дифракции.

Если в качестве периодического предмета используется решетка из прозрачных полосок шириной a и с периодом d ( e = a/d - скважность решетки), то контраст K получающегося самоизображения зависит от z в соответствии с графиком, приведенным на рис. 17 [86]. Видно, что ширина пика контраста вблизи плоскости саморепродукции по оси z примерно равна e D z , где D z определяется уравнением (32). Иными словами, с ростом структурной тонкости предмета (определяемой скважностью e ) сужается область наиболее контрастного распределения интенсивности около плоскости Тальбота [86]. Аналогичная зависимость наблюдается и для фазовой решетки, которая является моделью клеточной структуры биоткани, где величина периодической фазовой модуляции значительна, хотя бы из-за наличия стенок клетки.

Исходя из структуры когерентного поля, имеющего периодическую пространственную структуру, можно указать отличия между оптическими условиями внутривенного облучения крови в инвазивном и транскутанном способах (рис.18). В инвазивном варианте (рис. 18а) лазерное излучение, выходя из торца световода, введенного через полую иглу непосредственно в кровоток, образует световой конус. При неинвазивном транскутанном облучении (рис. 18б) излучение, периодически промодулированное прилегающей к кровотоку клеточной структурной биоткани, формирует в жидкости набор плоскостей Тальбота, похожий на “жаберные пластинки”.

 

 

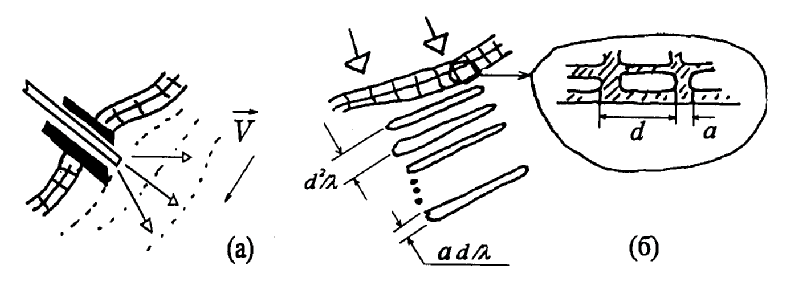
Рис. 17. Контраст К периодического изображения в зависимости от расстояния вдоль оптической оси -(б) - для предмета в виде амплитудной решетки с пропусканием -(а).

.

 

 

 

 

 

 

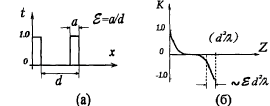
Рис. 18. Структура когерентного поля при внутривенном облучении инвазивным (а) и транскутанным (б) способами

Теоретически общее число плоскостей равно 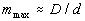, где D - диаметр освещающего пучка. Вблизи плоскостей Тальбота, где происходит наибольшая пространственная модуляция интенсивности света, за счет протекающей жидкости идет интенсивная диффузия продуктов фотохимической реакции в необлученные области крови. Из общих соображений следует, что режим облучения крови с формированием таких “жаберных” световых плоскостей позволяет подвергнуть биостимуляции большие объемы, чем при облучении сплошным конусом света.

Другим существенным эффектом, связанным с распространением излучения в клеточной структуре, является самореставрация изображения периодического предмета, имеющего сбои или дефекты в виде выпадения его малых структурных элементов. Суть этого эффекта состоит, согласно теоретическому и экспериментальному анализу [85], в следующем. Массив (2M+1)´ (2N+1) одинаковых изображений, каждое из которых имеет амплитудное пропускание te(x,y) и расположенных на прямоугольной двумерной решетке с периодами dx и dy, можно описать выражением:

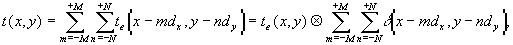(35)

где Ä означает свертку, а d (x,y) - дельта-функция. Фурье-образ такого предмета есть

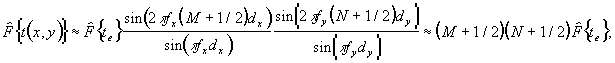(36)

Если в предмет (35) ввести дефекты в виде вакансий, т.е. убрать ряд составляющих элементарных изображений с пропусканием te(x,y), то выражение (35) следует заменить на

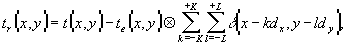(37)

где второе слагаемое соответствует массиву пустых клеток размером (2M+1)´ (2N+1). Можно показать [85], что в

этом случае Фурье-образ имеет вид: (38)

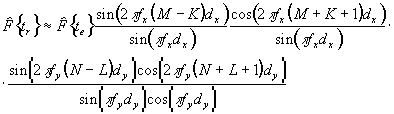
Из сравнения этого выражения с уравнением (36) видно, что Фурье-спектр периодического объекта с вакансиями есть спектр периодического объекта с измененным числом элементарных изображений, а именно [(M+1/2)-(K+1/2)]´ [(N+1/2)-(L+1/2)], промодулированный косинусои-дальным множителем. Из (38) видно, что при K<<M и L<<N дефектный периодический объект дает то же изображение, что и совершенный. Это связано с тем, что единичное изображение при саморепродукции формируется световым полем, дифрагировавшем на всех составляющих предмет элементарных изображениях [84,85].

Такая способность периодических полей к самореставрации позволяет объяснить одну из причин невлияния лазерного излучения на функционирование здоровых биотканей - эффект, хорошо известный в лазерной терапии. Световое излучение, проходящее через слой клеток, будет иметь периодическую структуру, мало подверженную влиянию “деформированных” клеток, если последних достаточно мало (до 5% согласно [85]). Если неискаженные клетки формируют поле, соответствующее совершенной клеточной структуре, то в “деформированных” клетках, попавших в это поле, могут каким-либо способом фотостимулироваться биопроцессы, стремящиеся минимизировать отклонение “деформированной” клетки от “правильного” поля.

Экспериментальные результаты

При экспериментальном исследовании дифракции на биологических объектах, использовался гелий-неоновый лазер ЛГ-222, с длиной волны излучения l =0,63 мкм, мощностью до 50 мВт, при диаметре пучка 2 мм и длиной когерентности не менее 15 см.

Биологические препараты готовились по следующей методике. Ткани растений помещались в раствор, содержащий активный хлор (для уничтожения сильно поглощающего излучение пигмента - хлорофилла) до полного обесцвечения. Затем они аккуратно промывались и помещались на предметное стекло. После испарения излишней воды, препарат заливался иммерсионной жидкостью и ламинировался покровным стеклом. Затем, приготовленный таким образом препарат в виде стеклянного сэндвича, помещался в оптическую схему.

Расстояние l между биологическим препаратом и плоскостью изображения (матовым экраном) было много больше размеров освещенной области самого препарата.

На рис. 19а. представлена фотография распределения интенсивности излучения, прошедшего через срез ткани лука, в зоне дифракции Фраунгофера. На фотографии явно видны дифракционные порядки. Расчет периода клеточной структуры по этому дифракционному изображению показал, что усредненный поперечный период решетки клеточной структуры лука составил 0,07 мм, что соответствует прямым измерениям на микроскопе ИМЦ-10. Средний поперечный период решетки, измеренный визуально, был равен d=0,067± 0,004 мм.

 

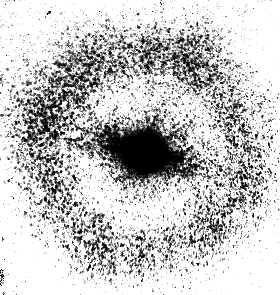
Рис.19а. Дифракция Фраунгофера на тканях лука. Линейная решетка

Рис.19б. Дифракция Фраунгофера на листе клена. Совокупность кружков.

На рис.19б. представлено изображение картины дифракции лазерного излучения на тканях листа клена. В этом случае дифракционная картина представляет собой кольцеобразную структуру с ярким пятном нулевого порядка. Такого рода дифракционные картины возникают в случае, если элементарный объект периодической структуры имеет приблизительно одинаковые размеры по оси x и y, и имеет округлую форму, подобно изображению, формирующемуся при дифракции лазерного излучения на матрице круглых отверстий.

В связи с тем, что пространственный спектр исследованных нами биологических объектов удовлетворяет критерию Монтгомери, то оказалось возможным получать самоизображения биологических объектов в плоскостях Тальбота. Фокусировка на разные плоскости Тальбота осуществлялась посредством передвижения микрообъектива вдоль оптической оси системы. Увеличенное изображение проецировалось микрообъективом на экран и фотографировалось с помощью зеркального фотоаппарата.

Исходя из периода клеточной структуры тканей лука и длины волны лазерного излучения, были рассчитаны расстояния от препарата тканей лука до плоскостей самоизображения, которое оказалось кратным 1,4 см.

На рис.20. представлена фотография, зарегистрированная в первой плоскости самоизображения, которая расположена на расстоянии z=d2/l =1,4 см. Как известно, на этом расстоянии наблюдается изображение периодического предмета, сдвинутое по фазе на p . На данном изображении видно, что границы клеток более темные, чем их сердцевина.

Рис.20. Самоизображение клеточной структуры тканей лука в плоскости с z=d2/l . Выделено дефектное место

Всего было получено семь плоскостей саморепродукции. Это косвенно подтверждает выводы сделанные в предыдущем разделе о том, что регулярная структура электромагнитного поля, несмотря на рассеяние, может влиять на эффект биостимуляции.

Для прямого подтверждения этой концепции были поставлены опыты по стимуляции образования соматических эмбриоидов в культуре клеток.

В экспериментах использовались растения линии Л-229, относящиеся к виду Solanum melongena L., Западно-азиатского подвида (ssp.occidentale Has.), а также линии Л - 271, Южно-азиатского подвида (ssp.meridionale Fil) и гибрида F1 Л-271 х Л-229. Растения выращивались в контролируемых условиях среды: фотопериод 16 часов, t=25+2 C, освещенность 3500- 4000 лк на среде Мурасиге и Скуга без гормональных добавок. Предварительно семена обрабатывались 15% хлорной известью в течение 20 минут с последующей пятикратной промывкой стерильной дистиллированной водой. Влияние физиологического состояния изучали на части этих же растений, перенесенных в холодную камеру для выращивания: t=15-18 C, фотопериод 12 часов, освещенность 3000-3500 лк.

Повторность в опыте от 5 до 20 эксплантов на вариант. В опытах регистрировали динамику образования соматических эмбриоидов в зависимости от воздействующего фактора.

Гибридизацию проводили традиционным методом с изоляцией. Гибридность F1 проверяли по доминантному маркерному признаку - наличию антоциановой окраски гипокотиля.

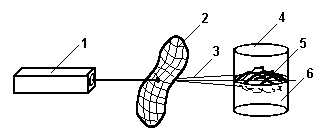
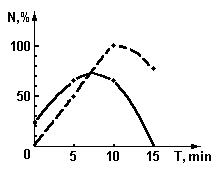
Рис. 21а. Оптическая схема для биологической стимуляции культуры клеток. 1 -лазер, 2 - лист, модулирующий электромагнитное излучение, 3 - модулированное лазерное излучение, 4 - стеклянная колба, 5 - культура клеток, 6 - питательная среда.

Рис. 21б. График зависимости количества образовавшихся зародышей от времени экспозиции излучением гелий-неонового лазера интесивностью 2,5 мВт/см2, модулированного листом растения.

¾ ¾ - для гипокотиля,

- - - - - - для тканей стебля.

Эксперимент проводился по схеме, показанной на рис 21.а. Контролируемым признаком была способность культуры клеток растения к образованию полноценных соматических эмбриоидов. Культуру клеток растения облучали через лист другого растения неразведенным лучом гелий-неонового лазера. Предполагалось, что пространственная модуляция электромагнитного излучения происходит по вышеописанному механизму. Мощность излучения после прохождения через лист была 2,5 мВт/см2. В эксперименте использовали лист растения у которого стимулируемый признак, проявлялся и без облучения.

На графиках зависимости количества образующихся зародышей от времени экспозиции, представленных на рис. 21б, наблюдаются экстремумы. Так для тканей каллуса экспозиция более 15 мин привела, по-видимому, к подавлению или полной пассивации процесса формирования зародышей. Более того, как видно из графика, при модулированном облучении культуры клеток полученных из стебля, контролируемый признак проявился. В тоже время без облучения или при облучении немодулированным излучением эта культура ткани не формирует зародышей растений.

Таким образом, эксперименты подтверждают выдвинутые предположения о влиянии электромагнитного поля на эффективность лазерной биостимуляции при условии согласования структуры поля со структурой биологического объекта.

11. Оптика биологических структур

Итак, распространение когерентного излучения в трехмерной периодической структуре приводит к формированию пространственно модулированных и локализованных по оси распространения распределений интенсивности света. Следует подчеркнуть, что проявления эффекта Тальбота не предполагают наличия у объекта каких-либо фокусирующих свойств. Кроме этого, известно, что эффект Тальбота наиболее ярко проявляется при высокой пространственной когерентности падающего излучения [84], что достигается использованием лазеров. Это подчеркивает еще один аспект важности когерентности излучения для ЛБС. Эффект Тальбота, как и эффект Лауэ, проявляется только при одновременном освещении всего периодического объекта, а не при его сканировании с помощью временной развертки лазерного луча - это может служить причиной различия режимов сканирующего и общего облучения в лазерных терапевтических применениях.

Таким образом, можно сделать общий вывод о том, что установившееся распределение интенсивности излучения в клеточной структуре слабо чувствительно к геометрическим параметрам освещающего пучка. Структура такого поля определяется параметрами клеточной структуры и длиной волны излучения и слабо зависит от дефектов клеточной структуры. Поэтому при разработке оптических систем для лазерных биомедицинских приборов следует стремится к минимизации энергетических потерь, а управление биостимулирующим эффектом осуществлять за счет временных параметров лазерного излучения (импульсное и сканирующее облучение, временная модуляция).

Роль нелинейно-оптических процессов. Лазерное излучение, попадая на живую ткань, проходит через сложную по структуре среду, имеющую квазижидкокристаллическое строение. Это обуславливает сильное изменение пространственного распределения интенсивности света, что проявляется как в появлении ярких линий-каустик, так и в возникновении “пятнистой” структуры поля по сечению пучка - спекл-структуры. Средний размер спекл-пятен и геометрические характеристики линий-каустик зависят от характеристик среды, через которую проходит свет и поэтому оказывается, что чем больший оптический путь пройден светом через биоткань, тем в большей степени его структурные характеристики - спекл-пятна и каустики - соответствуют характеристикам биоткани Такой механизм обратной связи при лазерном облучении обуславливает неминуемую подстройку фронта световой волны к структуре облучаемой ткани и объясняет биологическую эффективность ЛБС.

Высокая когерентность лазерного излучения и фазовый характер взаимодействия с биотканью приводят к быстрому (на малом отрезке оптического пути) изменению различных пространственно-временных распределений интенсивности света. Энергетически значимыми в смысле максимального воздействия на биоткань при этом оказываются распределения интенсивности, хорошо согласованные по микроструктуре с участком облучаемой биоткани Вследствие такой согласованности будет происходить эффективное возбуждение ансамблей биомакромолекул либо молекул-рецепторов, передающих свое возбуждение, например, молекулам нуклеиновых кислот С математической точки зрения такие процессы можно описывать в рамках фрактальной геометрии [27,28], тем более что и биологические ткани допускают также фрактальное описание. Под фрактальностью биоткани понимают то, что они имеют при разных масштабах увеличения подобную геометрическую структуру, которая может иметь дробную (фрактальную) размерность, а не быть только двух или трехмерной. В терминах фрактальной геометрии можно сказать, что изменение структуры светового фронта должно идти до тех пор, пока его фрактальная размерность не сравняется с фрактальной размерностью облучаемой биоткани, что обеспечит наилучшие условия возбуждения биологических структур и макромолекул [42].

Самоподобная (фрактальная) для разных масштабов рассмотрения пространственно-временная структура биоткани обуславливает механизм согласования характеристик электромагнитного поля с оптическими характеристиками среды при его прохождении через биовещество. “Безучастность” биоорганизма к облучению естественным светом связана с селективностью реакции сложной биомолекулы или клетки на воздействие света различных длин волн. Отсутствие биологического эффекта от естественного света связано с тем, что в этом излучении энергия, приходящаяся на частоту, на которую реагирует некоторая выделенная степень свободы молекулы, слишком мала, чтобы создать существенную вероятность возбуждения именно такой моды, с которой может быть связан запуск того или иного биологического механизма, хотя, в целом, пространственная плотность энергии в естественном свете может быть значительной [42].

Таким образом, когерентное излучение, попадая в биовещество, изменяет свое пространственное распределение интенсивности за счет оптической анизотропии живой ткани. При этом возникают явно выделенные в пространстве области - каустики, спекл-пятна - с высокой плотностью мощности лазерного излучения. Можно показать, что степень фокусировки излучения - величина максимальной плотности мощности - возрастает с ростом степени когерентности излучения Высокая плотность мощности излучения в этих областях, которые к тому же и согласованы по структуре с облучаемой тканью, обеспечивает возможность возникновения набора компонент излучения с комбинационными частотами за счет нелинейных эффектов, присущих живому веществу с квазижидкокристаллической структурой. Поскольку результирующий биологический эффект в обусловлен воздействием излучения с комбинационной частотой, которая, в свои очередь, определяется нелинейными характеристикам биоткани, то при этом нет критической зависимости от частоты падающего излучения Важно лишь то, что возникающие комбинационные частоты имеют дискретный, а не непрерывный спектр. Кратко можно сказать, что процесс взаимодействия лазерного излучения с живой тканью является самоорганизующимся: сама ткань меняет пространственные и частотные характеристики первоначального излучения, которое, в свою очередь, меняет оптические характеристики ткани за счет возбуждаемых биологических процессов. Такой подход к описанию механизма ЛБС примиряет кажущиеся противоречивыми требования когерентности, независимость терапевтического эффекта от длины волны когерентного излучения и отсутствие влияния естественного белого света. В работах сотрудников академика Н.Д.Девяткова [10] также обсуждались комбинационные частоты КВЧ-диапазона и отмечалось, что за счет комбинационных явлений дойти до оптического диапазона частот излучения не удается. При использовании лазеров ближнего ИК и видимого диапазона может, по всей вероятности, происходить “спуск” по шкале частот от оптического диапазона вниз до уровня КВЧ, и при этом нет запрета на возникновение явлений, хорошо изученных в медицине при действии КВЧ Такая динамика в качестве одного из своих аспектов может и должна содержать солитонные механизмы переноса энергии. зарядов и т.п. Формирование за счет фрактальных свойств биовещества спектра комбинационных частот когерентного излучения позволяет по-новому подойти к описанию терапевтического эффекта при сочетанном (например, двухволновом) лазерном облучении биологических объектов и. в частности, попытаться определить оптимальное соотношение интенсивностей при таком облучении.. Динамика изменения собственных оптических свойств живого объекта также, видимо, обеспечивает определенное согласование излучения со структурой биологической ткани. Пока эта возможность в более или менее полной мере используется для оценки биологической активности растительного объекта путем анализа временной декорреляции спекл-структур, формируемых лазерным излучением при рассеянии на поверхности объекта [87].

12. Генерализация локального процесса ЛБС

Рассмотренные физические концепции охватывают, по нашему мнению, все известные аспекты процесса ЛБС при медицинских терапевтических применениях и показывают достаточность для анализа ЛБС современной физики. Систематизируя, можно следующим образом сформулировать основные свойства и результаты исследований процесса взаимодействия лазерного излучения с биологическими объектами [88,93]:

- селективность лазерного воздействия: изменения индуцируются только в “больных” биосистемах, на “здоровые” клетки действие не оказывается;

- результат воздействия различен для образцов in vivo и in vitro;

- эффект ЛБС наблюдается и на неклеточных объектах типа пыльцы;

- при облучении белым светом подобного эффекта стимуляции не обнаружено;

- терапевтический эффект от ЛБС практически одинаков для лазерного излучения с любой длиной волны в диапазоне от 0,4 до 1,5 мкм;

- белковые молекулы in vitro не имеют полос поглощения для излучения в диапазоне длин волн от 0,4 до 1,5 мкм;

- эффект ЛБС наблюдается при интенсивностях 1 мВт/см2 и менее и малых энергетических дозах, определенных даже без учета доли отраженного и прошедшего через фазовый объект света (см., например, [88], стр. 115, если правильно посчитать по приведенным данным, то стимуляция сперматозоидов требует дозы 4,9 мДж/см2).

Среди медико-биологических последствий ЛБС в той или иной степени объективных и численно описываемых в обычной медицинской практике можно назвать такие, как снижение вязкости крови, стимуляция микроциркуляции крови в тканях, анальгезирующее действие, увеличение подвижности рецепторов клеток и отдельных клеток (например, сперматозоидов), стимуляция иммунной и нервной систем.

При рассмотрении и анализе эффекта ЛБС важно учитывать следующие основные свойства лазерного излучения:

- спектр излучения представляет собой узкий пик или набор таких пиков - “гребенку” - свойство монохроматичности лазерного излучения;

- лазерное излучение обладает высокими пространственной и временной степенями когерентности;

- лазерное излучение, кроме случая полупроводниковых лазеров, обладает высокой пространственной направленностью;

- для лазерного излучения характерна высокая интенсивность или яркость по сравнению с традиционными источниками света.

Необходимость анализа процесса ЛБС на уровне организма в целом инициируется все расширяющимися применением методик лазерной акупунктуры и внутривенного облучения крови. В настоящее время принято считать, что, независимо от первичных механизмов поглощения лазерного излучения, терапевтический эффект достигается при помощи интегрирующих систем организма - нервной, кровеносной и иммунной [89,90]. Более конкретного объяснения эффекта, чем то, что стремление этих систем к сохранению гомеостаза приводит к коррекции патологических процессов, пока нет. Выработка целостной концепции, конечно, затрудняется и отсутствием, например, научной теории акупунктуры.

Генерализация локального лазерного воздействия при ЛБС может быть объяснена в рамках концепции клеточных полей по А.Г.Гурвичу [8] с тем дополнением, что источником клеточного поля является не только хроматин, но и другие осцилляции и движения блобов, доменов и биомакромолекул. Результат воздействия передается в биоткани, по-видимому, по эстафетному механизму от клетки к клетке. При этом минимальными энергетическими потерями обладают такие конфигурации электромагнитного поля, которые соответствуют основной моде клетки. Из общих соображений понятно, что эти конфигурации должны соответствовать солитонным решениям волнового уравнения для клеточной среды. Энергоинформационный обмен между молекулами (клетками) посредством электромагнитных солитонов предполагает, что последние, будучи уединенными волнами, промодулированы всеми собственными частотами - естественно с различными весами - биологической макромолекулы (клетки). Тем самым “считывание” солитоном энергоинформационных характеристик с недефектных элементарных биологических структур (макромолекул, клеток и т.п.) обеспечивает относительно устойчивый их перенос к “потухшим” элементарным структурам, обеспечивая их “запуск”, а также разрушение дефектных структур и, возможно, синтез новых недефектных. Роль такого механизма переноса информации убедительно показана в монографии [10], посвященной диапазону миллиметровых волн.

В соответствии со стремлением любой системы к минимуму энергетических потерь биосистема в окружающее пространство излучает минимально возможное количество энергии в виде электромагнитного поля. Поэтому нативные клетки при нормальном функционировании имеют гладкую поверхность. Нарушение функций приводит, как указывалось выше, к росту градиента поля вблизи нарушений гладкой топологии оболочки клетки. Это инициирует более активное протекание обменных реакций в этих областях, способствующих “рассасыванию” либо исправлению “дефектной” клетки.

Когерентное излучение, попадая в биовещество, формирует разворачивающийся, четко разделенный во времени и пространстве, набор комбинационных частот и, поэтому, рано или поздно тот или иной молекулярный или конформационный переход получит “свою частоту” [91]. Тем самым, критической зависимости от частоты падающего излучения нет, важна лишь разделенность (с достаточным разрешением) появления комбинационных частот во времени. Очевидно, что при этом важен и факт наличия изначальной когерентности излучения. В случае, например, одной макромолекулы, несмотря на то, что ее структура может быть произвольной (спираль, фрактальная конформация), спектр слишком сложным, поглощенный электромагнитный квант падающего излучения будет последовательно “размениваться” сообразно с энергетической структурой молекулы (которая определяется, помимо всего прочего, ее конформационной структурой), обеспечивая тем самым запуск различных механизмов энергоинформационного обмена.

Кроме уже названного механизма переноса информации о недефектных структурах посредством модуляции “блуждающего” в биологической среде электромагнитного поля, необходимо предположить, что важную роль может также играть структурированная вода, в которой “растворены” молекулы биовещества. Действительно, согласно [92], структура макромолекулы и структура воды, которая эту макромолекулу окружает, согласованы друг с другом в смысле удовлетворения тем или иным условиям равновесия. Локально дефектная структура макромолекулы отражается в своем водном окружении. Стимулированное лазером появление набора комбинационных частот, несущих информацию о недефектных структурах (и которых неизмеримо больше, чем дефектных), может отражаться в появлении в той или иной форме волнообразных импульсов в водной среде. Последние достигают локально-дефектных участков биоткани и перестраивают в нужном направлении водное окружение дефектной молекулы. Затем, в силу условий равновесности для системы “структурированная вода + макромолекула”, происходит перестройка и самой макромолекулы.

Дополнительной информации о механизмах ЛБС организма в целом можно ожидать от исследований по применению методики тотального лазерного облучения пациента. Под тотальным лазерным облучением организма понимается воздействие на достаточно большие - более 10 см2 - участки поверхности тела [93, вып. 5, стр.114]. Эта методика получила жаргонное название “лазерный загар” в связи с внешним сходством процедуры с искусственным загаром. В какой-то степени принципы “лазерного загара” используются в гидролазерной системе [93], в которой лазерное излучение через волокно подается в обычный душ, струи которого выступают в качестве световодов, облучающих тело пациента. Очевидно, что в такой системе невозможно осуществлять контроль энергетической дозы облучения пациента.

Наконец, можно отметить, что концепция генерализации локального воздействия за счет межклеточной электромагнитной полевой связи применима не только к ЛБС, но и к таким процессам, как действие традиционных фармакологических и особенно гомеопатических препаратов. Действительно, чисто диффузионный механизм распространения лекарственного вещества по всей клеточной структуре вряд ли может быть доминирующим, по крайней мере, на начальном этапе. Начальный этап также может быть описан в терминах концепции квазичастиц - конформеров. Вполне возможно, что именно внешняя по отношению к организму часть межклеточного электромагнитного поля является ответственной за проявление феноменов “генного братства” и “кин-отбора” [94].

Квантовые аспекты ЛБС. Выше уже отмечалось, что на основе современной интерпретации квантовомеханического подхода необходимо учитывать информационную открытость биологических систем, участвующих в процессе ЛБС, которая приводит к нелокальности квантовых процессов и коллапсам волновых функций в результате “самоизмерений”[95]. Биосистема при этом обладает т.н. запутанной волновой функцией, описывающей когерентное состояние вещества, что приводит к нелинейному поведению всей сложной открытой системы, через которую могут протекать потоки энергии и информации(негэнтропии), и весь процесс в целом способен поэтому к самоорганизации. Вследствие этого свойства эффекта ЛБС могут быть объяснены и смоделированы в рамках обычных физических концепций с привлечением синергетических представлений. Как отмечалось выше, наличие иерархичности в многоуровневой структурной организации биологических систем указывает на возможность описания эффекта ЛБС в рамках нелинейно-динамической модели М.Фейгенбаума. При этом в качестве управляющего параметра выступает энергия дипольного или мультипольного момента биомакромолекулы в электромагнитном поле лазерного излучения. Этот механизм ответственен за ускорение процессов синтеза, например, ДНК и РНК, в которых участвуют макромолекулы с относительно большими дипольными моментами. С другой стороны, известна прямая аналогия между живым организмом и лазером, состоящая в том, что биологический организм, как и лазер, является нелинейной, упорядоченной открытой системой, включающей в себя в качестве составных частей аналоги активной среды, источника накачки и резонатора [61], и это позволяет надеяться на эффективность использования формализма квантовой радиофизики для описания эффекта ЛБС.

13. Заключение

Основной практический вывод, который необходимо сделать, состоит в том, что при ЛБС, кроме монохроматичности и когерентности, крайне важной оказывается хорошая направленность лазерного излучения высокой интенсивности, и поэтому использование, например, гелий-неоновых лазеров оказывается более эффективным, чем полупроводниковых.

Суммируя изложенное, можно сказать, что эффект ЛБС является нетривиальным примером взаимодействия двух неравновесных систем: когерентного поля и биологической системы. Несмотря, казалось бы, на необходимость “резонанса” этих двух систем по длине волны для возникновения взаимодействия, оно происходит всегда при монохроматичности излучения, что связано, видимо, с дискретностью энергетического спектра биосистемы и с изменением ее параметров во времени - она “дышит” и, тем самым, всегда обеспечивает резонанс структур. Основными чертами этого взаимодействия следует считать наличие самоорганизации и эквифинитности - независимости конечного результата от меняющихся в широких пределах начальных условий (длина волны, угол освещения, интенсивность и др.). Приведенные выше соображения в какой-то степени, по нашему мнению, объясняют, хотя бы на уровне аналогий, причины такой “однонаправленности” в сторону положительного терапевтического результата всего процесса лазерной биостимуляции. Предложенный подход, не отвергая уже известные представления о механизмах ЛБС, в определенной степени является обобщающим и показывает, что казалось бы, далекие друг от друга физические картины типа хаотизации через бифуркации и теплового нагрева излучением могут быть синтезированы в едином описании.

14. Благодарности

Авторы благодарят за плодотворные обсуждения и поддержку Е.В.Бомешко, В.В.Бирюкова, П.П.Гаряева, Л.П.Игнатьеву, С.П.Конопа, Л.Д.Писларюка, А.В.Марочкова и К.Г.Предко

15. Список литературы

  1. Низкоинтенсивные лазеры в медицине: Материалы Всесоюзного симпозиума в 2-х частях/ Под ред. А.Ф.Цыба и М.А.Каплана. - Обнинск: НИИМР АМН СССР. - 1991. - 134 + 141 с.

  2. Кару Т.И. Фотобиология низкоинтенсивной лазерной терапии./ Итоги науки и техники, серия физ. основы лазер. и пучков. технол.//ВИНИТИ. - 1989. - 4 - с.44-84.

  3. Илларионов В.Е. Основы лазерной терапии. - М.: РЕСПЕКТ - 1992 - 122 с.

  4. Давыдов А.С. Биология и квантовая механика. - Киев: Наукова думка. - 1979 - 296 с.

  5. Волькенштейн М.В. Общая биофизика. - М.: Наука - 1978. - 592 с.

  6. Лёви А., Сикевиц Ф. Структура и функции клетки. - М.: Мир - 1971 - 584 с.

  7. Шредингер Э. Что такое жизнь? С точки зрения физика.- М.: Атомиздат - 1972-154 с.

  8. Гурвич А.Г. Принципы аналитической биологии и теории клеточных полей. - М.:Наука - 1991. -288 с.

  9. Гаряев П.П. Волновой геном.- М.: Общ. польза.- 1994 - 280 с.

  10. Девятков Н.Д., Голант М.Б., Бецкий О.В. Миллиметровые волны и их роль в процессах жизнедеятельности. - М.: Радио и связь. - 1991. - 168 с.

  11. Мизнер Ч., Торн К., Уилер Дж. Гравитация. - Бишкек: Айнштайн - 1994. - т.1 -474 с.

  12. Делоне Н.Б. Взаимодействие лазерного излучения с веществом. - М.:Наука - 1989. - 280 с.

  13. Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическая биофизика. - М.: Наука - 1984. -304 с.

  14. Климонтович Ю.А. Статистическая теория открытых систем. - М.: ТОО “Янус” - 1995. - 624 с.

  15. Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. - М.: Наука. - 1989. - 344 с.

  16. Kompanets I.N., Krasnov A.E., Malov A.N. The interaction of laser light with biologic tissue. //Photonics and Optoelectronics. - 1995. - v.3, N 1. -p. 115-122.

  17. Шульц Г., Ширмер Р. Принципы структурной организации белков. - М.: Мир - 1982. - 356 с.

  18. Malov A.N., Malov S.N., Festchenko V.S. Resonance nature of laser biostimulation from the point of view of quasi-optics. //Laser Physics. - 1996 -v.6, N 5 - p.979-982.

  19. Проблема белка. Том 3: Структурная организация белка / Е.М.Попов. – М.: Наука, 1997. – 604 с.

  20. Рубин А.Б. .Биофизика. – М.: Высшая школа, 1987. – 319 + 305 с.

  21. Малов А.Н.,Малов С.Н., Черный В.В. Лазерная биостимуляция как самоорганизующийся неравновесный процесс / Тезисы IV Межд. Конгресса “Проблемы лазерной медицины” - Москва-Видное, 1997, с.278-279.

  22. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Наука - 1973. -504 с.

  23. Чернавский Д.С. Биофизика. //Физическая энциклопедия. - М.: Бол. Росс. энциклопедия . - 1992 - т.1. - с. 203-209.

  24. Карлов Н.В., Кириченко Н.А. Лукьянчук Б.С. Лазерная термохимия. - М.: ЦентрКом. - 1994. - 368 с.

  25. Kazmaier P.M., McKerrow A., Buncel E. Molecular modeling of photoactive pigments. //Is and T`s 44 th. Annu. Conf., St. Paul, Minn., May 12-17, 1991: Adv. Print Pap. Summ. - Springfield (Va), 1991 - p. 575-576.

  26. Коротков К.Г. Свет после жизни. Экспериментальные исследования биофизической активности тела после смерти. - Спб: 1994. - 110 c.

  27. Федер Е. Фракталы. - М.: Мир - 1991. - 254 с.

  28. Фракталы в физике / Под ред. Л.Пьетронеро. -М.:Мир -1988.-672 с.

  29. Козлов В.И., Мельман Е.П., Нейко Е.М., Шутка Б.В. Гистофизиология капилляров. – СПб.: Наука, 1994. – 234 с.

  30. Броудай М., Мерей Дж. Физические основы микроэлектроники.–М: Мир, 1985.–496с.

  31. Фридрихсберг Д.С. Курс коллоидной химии –СПб: Химия, 1995.–400с.

  32. Вундерлих Б. Физика макромолекул. Т. 1– М: Мир, 1976.–624с., Вундерлих Б. Физика макромолекул. Т. 2– М: Мир, 1976.–574с.

  33. Моро У. Микролитография. В 2-х тт.–М: Мир, 1990.–605+632с.

  34. Rowlinson J.S. Widom B. Molecular Theory of Capillarity. - Oxford: Clarendon Press, 1982.

  35. Аграфонов Ю.В., Тихонов Д.А., Саркисов Г.Н., Мартынов Г.А. Дипольная жидкость вблизи поверхности. Метод теории возмущений. Синглетное приближение. // Коллоидный журнал, 1992, т. 54, № 1, стр. 3-13.

  36. Аграфонов Ю.В. Структура жидкости вблизи твердой цилиндрической поверхности. // Коллоидный журнал, 1994, т. 56, № 4, стр. 473-476

  37. Тихонов Д.А., Аграфонов Ю.В. Мартынов Г.А. и др. //Коллоид. Журн. 1991. Т.53.№5.с.911

  38. Мартынов Г.А. Проблема фазовых переходов в статистической механике. УФН, 169, № 6, с. 595 – 624.

  39. Саркисов Г.Н. Приближенные уравнения теории жидкостей в статистической термодинамике классических жидких систем. УФН, 169, № 6, с. 625 – 642.

  40. Аграфонов Ю.В., Балахчи А.Г., Бирюлина Т.В., Выговский Ю.Н., Дорогобид Я.С., Кручинин Л.Е., Малов А.Н., Ушаков Ф.Е., Черный В.В. Граничные структуры жидкости и голографические регистрирующие среды.. \\ Компьютерная оптика, (1999), вып. 19, с. 118 – 124.

  41. Agrafonov Yu.V., Martynov G.A., Sarkisov G.N. //Molecular Physics. 1980. V. 39. N 4. P. 963.

  42. Малов А.Н., Малов С.Н., Черный В.В. Физические основы лазерной терапии. \ Иркутск: ИФ ИЛФ СО РАН, 1997. – препринт № 2. –46 с.

  43. Твердислов В.А., Тихонов А.Н., Яковенко Л.В. Физические механизмы функционирования биологических мембран. / М : МГУ, 1987.

  44. Аграфонов Ю.В., Балахчи А.Г., Дорогобид Я.С., Малов А.Н. Влияние структуры примембранной воды на эффект лазерной биостимуляции. / В кн.: “Люминесценция и сопутствующие явления”. – Иркутск: ИГУ, 1999. – с. 65 – 70.

  45. Габуда С.П. Связанная вода.–Новосибирск: Наука, 1982,-160с.

  46. Конев С.В. Структурная лабильность биологических мембран и регуляторные процессы./АН БССР, Ин-т фотобиологии - Минск: Наука и техника, 1987.

  47. Яшкичев В.И. Вода, движение молекул, структура, межфазные процессы и отклик на внешнее воздействие. 1996, М.-“АГАР”.

  48. Malov A.N., Malov S.N., Feshchenko V.S. Resonance nature of laser biostimulation from the point of view of quasi-optics.// Laser Physics, 1996, 6, N 5, pp. 979 – 982.

  49. Марочков А.В. Внутривенное лазерное облучение крови, механизм воздействия и клиническое применение. – Минск: Полибиг – 1996.

  50. Кемп П., Армс К. Введение в биологию. – М.: Мир – 1988.- 671 с.

  51. Педли Т. Гидродинамика крупных кровеносных сосудов. – М: Москва – 1983.

  52. Павловский Ю.Н.О пристеночном эффекте. / “Механика жидкостей и газов”. –(1967), № 2, стр. 160

  53. Vigovsky Yu.N., Konop S.P., Malov A.N., Malov S.N. Photoinduced phase transitions in hologram recording in layers of dichromated gelatin.// Laser Physics, (1998), vol.8, N 4, pp. 901 – 915.

  54. Илларионов В.Е. Техника и методики процедур лазерной терапии. Справочник. - М.: Лазер маркет - 1994. - 178 с.

  55. Илиел Э., Аллинджер Н., Энжиал С., Моррисон Г. Конформационный анализ. - М.: Мир - 1969. - 592 с.

  56. Дашевский В.Г. Конформационный анализ органических молекул. - М.: Химия - 1982. - 272 с.

  57. Гудвин Б. Временная организация клетки. - М: Мир - 1966 - 252 с.

  58. Де Жен П. Идеи скейлинга в физике полимеров. - М.: Мир - 1982 - 240 с.

  59. Крюков А.И., Шерстюк В.П., Дилунг И.И. Фотоперенос электрона и его прикладные аспекты. - Киев: Наукова думка - 1982. - 240 с.

  60. Лисиенко В.И. Структурная альтерация биологических жидкостей - основа клинического применения лазера в практике лечения хирургических больных // Laser Market - 1995 - №2-3 - с.9-12.

  61. Cin Qiao. Analogy between life phenomenon and laser //Chin. J. Infrared Res. A. - 1989. v.8, N1. - p. 69-74.

  62. Файн В.М. Квантовая радиофизика. Т.1. Фотоны и нелинейные среды. - М.: Сов.радио.- 1972. - 472 с.

  63. Волостников В.Г., Котляр В.В., Малов А.Н.. Подвигин В.Н., Клибанов М.В., Абрамочкин Е.Г. Обратные задачи рассеяния в когерентно-оптической диагностике промышленных изделий./ - М.: ФИАН СССР - 1985 - препринт №110. - 45 с.

  64. Коноп С.П., Константинова А.Г., Малов А.Н. Самопроявляющаяся регистрация голограмм на основе конформационных переходов в хромированных желатин-глицериновых системах. / В сб. “Применение лазеров в науке и технике”. -Вып.8. - Иркутск: ИФ ИЛФ СО РАН. - 1996. - с.51-58.

  65. Konop S.P., Konstantinova A.G., Malov A.N. Mechanism of the hologram recording in “self-developed” dichromated gelatin layers.// Photonics and Optoelectronics. - 1995 - v.3, N 1. - p.21-26.

  66. Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. Нестационарные структуры и диффузный хаос. - М.: Наука - 1992. - 544 с.

  67. Гласс Л., Мэки М. От часов к хаосу: ритмы жизни. - М.: Мир. 1991. - 248 с.

  68. Шустер Г. Детерминированный хаос. - М.: Мир. - 1988. - 240 с.

  69. Воронина О.Ю., Каплан М.А., Степанов В.А. Нерезонансный механизм биостимулирующего действия низкоинтенсивного лазерного излучения // Физическая медицина. - 1992. - т.2, № 1-2. - с.40-50.

  70. Тучин В.В. Основы взаимодействия низкоинтенсивного лазерного излучения с биотканями: дозиметрический и диагностический аспекты. // Изв. РАН: Сер.физич. - 1995 - т.59, №6 - с.120-143.

  71. Утц С.Р., Тучин В.В., Ярославский И.В., Утц И.А., Цуканов В.А., Барабанов А.Ю. Оптимизация метода облучения крови с учетом данных о распространении лазерного излучения в биотканях // Лазерная физика - 1992. - №3 - с.109-117.

  72. Оптическая голография. /Под ред. Г.Колфилда. - М.: Мир - 1982 - 736 с.

  73. Tuchin V.V. Lasers and fiber optics in biomedicine // Laser Physics. - 1993 -v.3, N 4 - p. 767-820.

  74. Джеймс Т.Х. Теория фотографического процесса. - Л.: Химия. - 1980 - 672 с.

  75. Никольский В.В. Электродинамика и распространение радиоволн. - М.:Наука. - 1973. - 608 с.

  76. Ваганов Р.Б., Каценеленбаум Б.З. Основы теории дифракции. - М.: Наука. - 1982. - 272 с.

  77. Каценеленбаум Б.З. Высокочастотная электродинамика. - М.: Наука. - 1966.

  78. Боровиков В.А., Кинбер Б.Е. Геометрическая теория дифракции. - М.: Наука, - 1978.

  79. Голуб М.А., Сисакян И.Н., Сойфер В.А. Моданы - новые элементы компьютерной оптики. // Компьютерная оптика. - 1990. -№8 - с.3-64.

  80. Ярив А. Квантовая электроника и нелинейная оптика. - М.: Сов.радио. - 1973. - 456 с.

  81. Солимено С., Крозиньяни Б., Ди Порто П. Дифракция и волноводное распространение оптического излучения. - М.: Мир. - 1989.- 664 с.

  82. Malov A.N. Control over information characteristics of coherent optical systems. // Laser Physics. - 1993 -v.3, N 1 - p. 193-203.

  83. Эшби У.Р. Введение в кибернетику. М.: Изд.иностр.лит. - 1959 - 286 с.

  84. Patorsky K. The self-imaging phenomenon and its application // In “Progress in Optics” /Ed. E.Wolf. - Elsevier Publ., New York, - 1989 - v.27 - p.3-108.

  85. Kalestynski A., Smolinska B. Self-restoration and the autoidolon of defective periodic objects // Optica Acta. - 1978 - v.25, N 2 - p. 125-134.

  86. Chavel P., Strand T.C. Range measurement using Talbot diffraction imaging of gratings // Applied Optics. - 1984. - v.23, N 6. - p.862-871.

  87. Oulamara A., Tribillon G., Duvernoy J. Biological activity measurement on botanical speciemen surfaces using a temporal decorrelation effect of laser speckle. // J. Mod. Opt. – 1989. –36, N 2. – pp. 165 – 179

  88. Прикладные проблемы лазерной медицины. - М.: МАКДЭЛ. - 1993. -188 с.

  89. Козлов В.И., Буйлин В.А. Лазеротерапия. - М., Владивосток: центр “АСТР-Востокмедтехника сервис” - 1992. - 164 с.

  90. Корепанов В.М. Теория и практика лазерной терапии. В трех частях. - М.: ЛазерМед. - 1992. - 195 с.

  91. Малов А.Н., Костюк М.Г. Модельный анализ основных биологических процессов в низкоинтенсивной лазерной терапии // Laser Market. - 1995. -N 1 - c. 37-39.

  92. Бульенков Н.А. Периодические диспирационно-модульные алмазоподобные структуры связанной “воды” - возможные конструкции, определяющие конформацию биополимеров в структурах их гидратов. // Кристаллография. - 1988. - т.33, №2. - с. 424-444.

  93. “Применение лазеров в науке и технике:

  • вып.1 - Иркутск: ОАТФ ИНЦ СО АН СССР - 1988 - 50 с.

  • вып.2. - Тольятти: НТЦ ПО “АвтоВАЗ” -1989 - 150 с.

  • вып.3. - Иркутск: ОАТФ ИНЦ СО АН СССР - 1990 - 148 с.

  • вып.4. - Тольятти: МП “Самара Интер Синтез” - 1991 - 157 с.

  • вып.5. - Новосибирск: ТОО “СиЛаП” - 1992 - 170 с.

  • вып.6. - Иркутск: ИФ ИЛФ СО РАН - 1994 - 158 с.

  • вып.7. - Иркутск: ИФ ИЛФ СО РАН - 1995 - 76 с.

  • вып.8. - Иркутск: ИФ ИЛФ СО РАН - 1996 - 210 с.

  • вып.9.-.Иркутск. ИФ ИЛФ СО РАН – 1997 – 214 с.

  1. Докинз Р. Эгоистичный ген. - М.: Мир. - 1993. - 318 с.

  2. Кадомцев Б.Б. Динамика и информация. 2-е изд. – М.: Редакция журнала “Успехи физических наук”, 1999. – 400 с.
Ќ § ¤‚ ­ з «®
 

Copyright © 1999-2004 MeDia-security, webmaster@media-security.ru
  MeDia-security: Новейшие суперзащитные оптические голографические технологии, разработка и изготовление оборудования для производства и нанесения голограмм.Методика применения и нанесения голограмм. Приборы контроля подлинности голограмм.  
  Новости  
от MeDia-security

Имя   

E-mail

 

СРОЧНОЕ
ИЗГОТОВЛЕНИЕ
ГОЛОГРАММ!!!
г.Москва, Россия
тел.109-7119
vigovsky@media-security.ru
Голограммы.Голограммы
на стекле.Голограммы на
плёнке.Голографические
портреты.Голографические
наклейки.Голографические
пломбы разрушаемые.
Голографические стикеры.
Голографическая фольга
горячего тиснения - фольга полиграфическая.
HOLOGRAM QUICK PRODUCTION!!!
Moscow, Russia
tel.+7(095)109-7119
vigovsky@media-security.ru
Holograms. Holograms on glass. Holographic film. Holographic portraits. Holographic labels. Holographic destructible seals. Holographic stickers. Holographic foil for hot stamping - polygraphic foil.