УНИТАРНОЕ
СМЕШИВАНИЕ СКАЛЯР-ВЕКТОР В 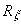 КАЛИБРОВКЕ
КАЛИБРОВКЕ
А.Е. Калошин, А.Е. Раджабов
Иркутский Государственный Университет
Рассматривается эффект
унитарного смешивания
скалярного и векторного полей возникающий при
суммировании петлевых
диаграмм в случае, если векторный ток
не является сохраняющимся.
В произвольной
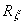 -калибровке
получены решения уравнений Дайсона
и осуществлена
перенормировка полных пропагаторов.
-калибровке
получены решения уравнений Дайсона
и осуществлена
перенормировка полных пропагаторов.
В последние годы вопрос об "одевании" векторного бозона (превращение его в частицу с конечной шириной) много раз обсуждался в литературе [1,2,3]. Обсуждение во многом связано с экспериментами по рождению калибровочных бозонов W и Z. Повышение точности измерений приводит к необходимости вычисления поправок более высокого порядка, что порождает ряд теоретических проблем.
В данной работе рассматривается не совсем стандартный эффект, связанный с "одеванием" векторного бозона. В случае, когда существует подходящая по квантовым числам скалярная частица возможны петлевые переходы скаляр-вектор. В этом нет никакого противоречия с сохранением спина, так как в векторном поле существует лишняя степень свободы, связанная со спином 0. Петлевые переходы как раз и возникают между этой степенью свободы и скалярным полем.
Наиболее интересен этот
вопрос в электрослабых моделях,
где возможно унитарное смешивание между калибровочными бозонами
и хигсовскими
скалярами. Этот эффект отсутствует в стандартной модели (см.,
например, [4]),
но появляется в расширенных моделях с большим числом хигсовских
частиц. В электрослабых
моделях исследование унитарного смешивания осложняется
наличием переходов
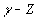 и
возможно большого количества хигсовских частиц.
Другим усложняющим
фактором является наличие "духовых" частиц [5] в
произвольной
и
возможно большого количества хигсовских частиц.
Другим усложняющим
фактором является наличие "духовых" частиц [5] в
произвольной 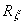 калибровке,
которая является наиболее употребительной в
электрослабых теориях
[6]. Другой
физической системой, в которой существует этот эффект,
является система
адронов
калибровке,
которая является наиболее употребительной в
электрослабых теориях
[6]. Другой
физической системой, в которой существует этот эффект,
является система
адронов 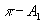 ,
рассмотрение которой во многих аспектах
проще. Ниже мы рассматриваем такую систему в произвольной
,
рассмотрение которой во многих аспектах
проще. Ниже мы рассматриваем такую систему в произвольной
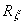 калибровке.
В такой модели можно проследить зависимость от
калибровочного
параметра
калибровке.
В такой модели можно проследить зависимость от
калибровочного
параметра 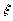 при унитарном смешивании, а также исследовать
процесс перенормировки, т.к. при унитарном смешивании
и наличии "духовых"
частиц он становится далеко не тривиальным.
при унитарном смешивании, а также исследовать
процесс перенормировки, т.к. при унитарном смешивании
и наличии "духовых"
частиц он становится далеко не тривиальным.
Система
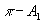
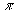 и
и
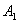 "одеваются" через трехпионое промежуточное
состояние, экспериментальным
фактом является то, что эти три пиона
рождаются в квази-двухчастичном
виде: либо
"одеваются" через трехпионое промежуточное
состояние, экспериментальным
фактом является то, что эти три пиона
рождаются в квази-двухчастичном
виде: либо 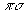 ,
либо
,
либо 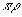 .
Ниже мы учитываем только
.
Ниже мы учитываем только 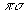 промежуточное состояние. Свободный
лагранжиан системы записывается
в виде [7]:
промежуточное состояние. Свободный
лагранжиан системы записывается
в виде [7]:
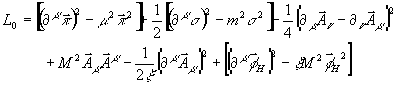
Отсюда следуют :
пропагатор
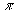 мезона
мезона 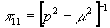
пропагатор
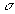 мезона
мезона
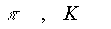
пропагатор "духа" 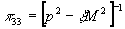
пропагатор векторного бозона в 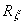 калибровке
калибровке
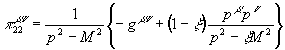
Здесь и далее индекс
1 соответствует 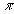 мезону, 2
мезону, 2 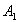 мезону, 3
"духу".
Лагранжиан взаимодействия дается формулой:
мезону, 3
"духу".
Лагранжиан взаимодействия дается формулой:

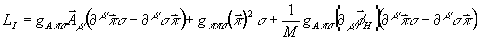
и приводит к вершинам:
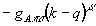
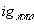
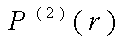
Формализм S-V смешивания
Превращение затравочного пропагатора в полный наиболее наглядно осуществляется с помощью уравнений Дайсона. Однако в нашем случае из-за тензорной структуры продольная и поперечная компонента пропагатора векторной частицы будет одеваться по разному, поэтому векторный пропагатор и векторную петлю нужно разделить на продольную и поперечную части:
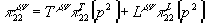 ,
, 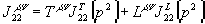
где введены обозначения
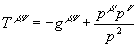 ,
,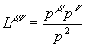 ,
,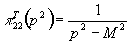 ,
,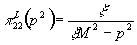
В случае, когда имеется подходящая по квантовым числам скалярная частица и векторный ток не является сохраняющимся, ситуация меняется. Возникают петли, связывающие между собой скалярные и векторные пропагаторы и в результате суммирования появляются новые объекты - полные переходные пропагаторы. Система уравнений Дайсона в данном случае будет выглядеть следующим образом:
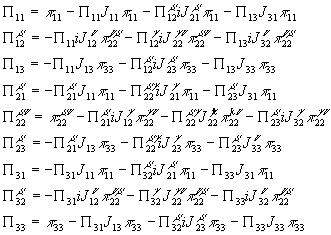
Для удобства
из 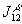 и
и 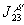 выделен множитель
выделен множитель
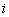 .
Следующим шагом
будет разделить
.
Следующим шагом
будет разделить 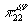 и
и 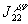 на продольную и поперечную части. При этом
введем скалярные
функции:
на продольную и поперечную части. При этом
введем скалярные
функции:
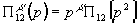 ,
,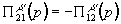 ,
,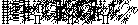 ,
,
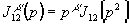 ,
,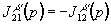 ,
,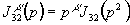 ,
,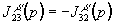
В результате поперечная компонента отщепляется, остается только одно уравнение:
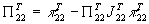
А на продольные компоненты получается система уравнений:
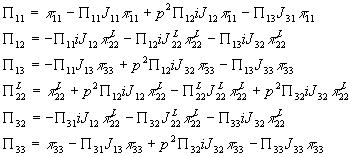 (1)
(1)
Решением системы будет
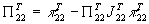
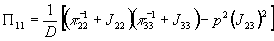 ,
,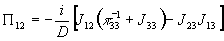
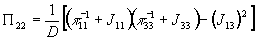 ,
,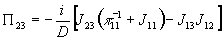 (2)
(2)
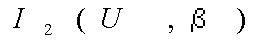 ,
,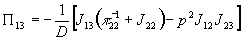
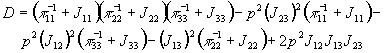
Явный вид петель
Петли
имеют вид 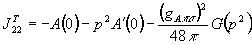
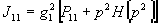 ,
,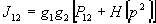 ,
,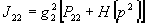
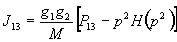 ,
,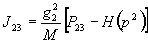 ,
,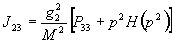
Для удобства введены
коэффициенты 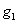 ,
,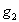 и функции
и функции
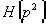 ,
,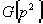
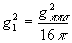 ,
,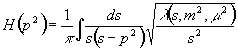
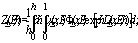 ,
,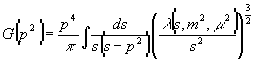
Явный вид полиномов 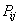 определится при перенормировке. Следует
однако отметить, что
определится при перенормировке. Следует
однако отметить, что 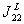 связана с
связана с 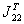 условием: член
нулевого порядка полинома
условием: член
нулевого порядка полинома 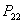 должен быть равен
должен быть равен
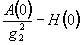 .
При этом в пропагаторах сократятся
члены с
.
При этом в пропагаторах сократятся
члены с 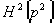 ,
а в знаменателе
,
а в знаменателе 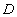 члены
члены
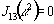 и
и 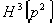 .
.
Перенормировка
Перенормировку произведем
с помощью вычитания на массовой поверхности
[8], т.е. будем считать, что 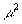 и
и 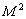 - перенормированные массы пиона и
- перенормированные массы пиона и 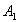 -
мезона.
-
мезона.
Для перенормировки поперечной
части векторного пропагатора требуется
два раза вычесть 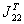 на полную ширину
резонанса.
на полную ширину
резонанса.
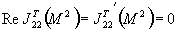
С помощью этого определяются
две произвольные константы 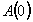 и
и 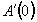 .
.
В случае связанных пропагаторов
условия перенормировки будут другими.
Рассмотрим внимательнее скалярный пропагатор. Условие
того, что функция
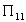 обладает полюсом
в точке
обладает полюсом
в точке 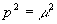 с единичным
вычетом следует прямо из первого уравнения (1)
с единичным
вычетом следует прямо из первого уравнения (1)
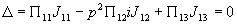 ,
,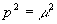 (3)
(3)
С учетом
решений (2) 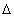 можно переписать в виде
можно переписать в виде
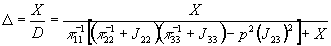
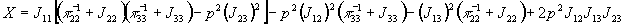
Отсюда видно, что уравнение (3) приводит к следующим условиям
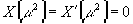
Это должно выполняться
при любом калибровочном параметре 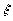 .
Выделим в
.
Выделим в 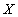 части
части 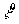 ,
,
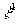 и
и 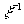 в явном виде
в явном виде
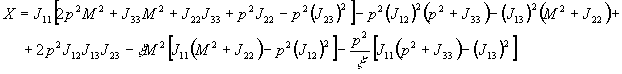
Условие 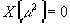 вне зависимости от калибровочного параметра
вне зависимости от калибровочного параметра
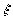 (части при разных степенях
(части при разных степенях 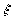 зануляются независимо) приведет
к системе из трех уравнений. Считая константы независимыми
друг от друга,
мы получим следующие условия на петли:
зануляются независимо) приведет
к системе из трех уравнений. Считая константы независимыми
друг от друга,
мы получим следующие условия на петли:
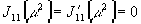 ,
,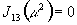 ,
,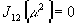
Теперь рассмотрим перенормировку
полюса при 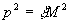 .
Полюс в пропагаторах
порождается нулями функции
.
Полюс в пропагаторах
порождается нулями функции 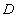 .
Затравочная функция
.
Затравочная функция
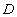 имела нуль второго порядка, который должен
присутствовать
в ней и после "одевания". Т.к. константы связи
независимы, это
приводит к условиям:
имела нуль второго порядка, который должен
присутствовать
в ней и после "одевания". Т.к. константы связи
независимы, это
приводит к условиям:
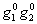
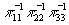 - нуль второго
порядка
- нуль второго
порядка
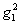
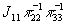 - нуль второго
порядка
- нуль второго
порядка
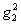
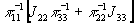 - нуль второго
порядка
- нуль второго
порядка
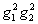
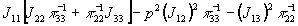 - нуль второго
порядка
- нуль второго
порядка
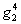
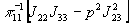 - нуль второго
порядка
- нуль второго
порядка
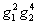
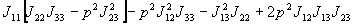 - нуль второго
порядка
- нуль второго
порядка
Потребуем, чтобы 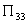 имел полюс в точке
имел полюс в точке 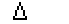 с
единичным вычетом
(как у
с
единичным вычетом
(как у 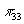 ).
Из (1)
и (2)
возникают условия на функцию
).
Из (1)
и (2)
возникают условия на функцию 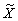 :
:
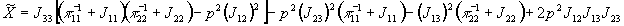
Функция 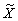 должна обладать
нулем третьего порядка в точке
должна обладать
нулем третьего порядка в точке 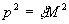 ,
следовательно:
,
следовательно:
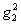
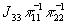 - нуль третьего
порядка
- нуль третьего
порядка 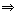
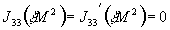
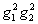
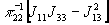 - нуль третьего
порядка
- нуль третьего
порядка 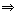
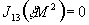
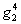
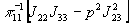 - нуль третьего
порядка
- нуль третьего
порядка
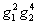
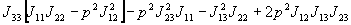
Аналогичное требование
на 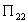 приведет условию
на функцию
приведет условию
на функцию 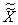
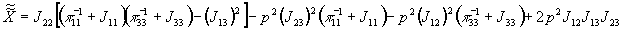
Функция
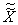 также должна обладать
нулем третьего порядка в точке
также должна обладать
нулем третьего порядка в точке 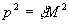 :
:
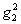
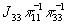 - нуль третьего
порядка
- нуль третьего
порядка 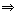
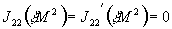
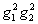
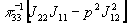 - нуль третьего
порядка
- нуль третьего
порядка 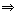
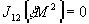
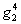
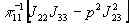 - нуль третьего
порядка
- нуль третьего
порядка 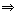
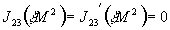
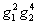
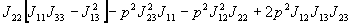
В результате перенормировки пропагаторов получаются следующие условия на петли:
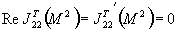 ,
,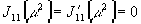 ,
,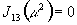 ,
,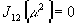
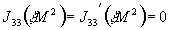 ,
,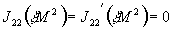
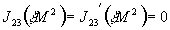 ,
,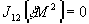 ,
,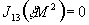
Заключение
Итак, при наличии петлевых
S-V переходов возникает система уравнений
для пропагаторов, и в результате полные пропагаторы имеют
более сложный вид(см.
также [9]).
Так как была выбрана 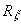 -калибровка вид
пропагаторов осложняется наличием "духовых"
частиц, которые
тоже участвуют в игре. Модель, рассмотренная выше,
хоть и физическая,
но была выбрана в основном из методических
соображений, с
целью развития формализма S-V смешивания.
-калибровка вид
пропагаторов осложняется наличием "духовых"
частиц, которые
тоже участвуют в игре. Модель, рассмотренная выше,
хоть и физическая,
но была выбрана в основном из методических
соображений, с
целью развития формализма S-V смешивания.
Естественным продолжением данной работы будет рассмотрение данного эффекта в электрослабых теориях.
Литература
- H.Veltman, Mass and width of unstable gauge bosons. // Zeit. fur Phys., C62 (1994),p.35-51
- E.N. Argyres et al, Stable calculations for unstable particles : restoring gauge invariance.// Phys. Lett. B358 (1995), p. 339
- M. Nowakowski , A.Pilaftsis, On gauge invariance of Breit-Wigner propagator. // Z. Phys. C60 (1993) p.121-125
- Окунь Л.Б. Лептоны и кварки. М: Наука, 1990.
- Тейлор Дж. Калибровочные теории слабых взаимодействий. М:Мир, 1978.
- E.S. Abers, B.W. Lee, Gauge theories. // Phys. Reports 9(1973) p.1-125
- Т.-П. Ченг, Л.-Ф. Ли. Калибровочные теории в физике элементарных частиц. М: Мир, 1987.
- Боголюбов Н.Н., Ширков Д.В. Введение в теорию квантованых полей. М: Наука, 1976.
Калошин А.Е. Унитарное смешивание в системе скаляр-вектор.//Ядерная физика, т.60,1997, №7, с.1306-1312

