РОЖДЕНИЕ ЧАРМА И СПЕКТРЫ МЮОНОВ НА БОЛЬШИХ ГЛУБИНАХ ПОД ВОДОЙ
В. А. Наумов, Т. С. Синеговская, С. И. Синеговский
Иркутский государственный университет
Оценки вклада прямых атмосферных мюонов нa глубинах действующих и проектируемых глубоководных нейтринных телескопов (1-4 км), сделанные для нескольких моделей рождения чарма (кварк-глюонных струн, рекомбинационная кварк-партонная, пертурбативные КХД-модели), показывают, что даже сравнительно небольшие глубины, такие как в месте расположения Байкальского нейтринного телескопа, все-таки дают потенциальную возможность обнаружить прямые мюоны - для не слишком больших зенитных углов (70°
-80°
) и при увеличении порога регистрации до 100 ТэВ.
1 Введение
Исследование рождения
чарма в адронных взаимодействиях представляет интерес не только
для физики частиц, но и имеет важный прикладной аспект в физике
атмосферных нейтрино и нейтринной астрономии высоких энергий:
атмосферные нейтрино от распада очарованных адронов являются
основным источником фоновых событий в при детектировании нейтрино
внеземного происхождения – квазидиффузного потока нейтрино
от активных галактических ядер [1]. Вопрос
о вкладе в поток атмосферных мюонов (АМ), прямых мюонов (ПМ),
т.е. мюонов от распадов очарованных частиц (D±-,
D0-, 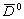 -
мезонов и Lc+-гиперонов),
которые рождаются во взаимодействии космических лучей с атмосферой
Земли, все еще остается нерешенным, несмотря на длительную
историю [2].
Данные наземных измерений потоков мюонов высоких энергий и
подземных детекторов зачастую настолько противоречат друг
другу, что извлечение информации о чарме представляет трудноразрешимую
задачу, если вообще возможно [3].
Точность измерений на подземных установках существенно ограничена
неопределенностями плотности и химического состава окружающего
установку грунта. Уместно поэтому, вспомнить такие важные
преимущества подводных черенковских установок, как высокая
степень однородности вещества–поглотителя (вода, лед) и большой
детекторный объем, и обсудить потенциальные возможности нейтринных
телескопов (AMANDA [4],
Байкальский НТ [5], NESTOR [6])
в контексте измерения вклада ПМ и исследования моделей рождения
чарма.
-
мезонов и Lc+-гиперонов),
которые рождаются во взаимодействии космических лучей с атмосферой
Земли, все еще остается нерешенным, несмотря на длительную
историю [2].
Данные наземных измерений потоков мюонов высоких энергий и
подземных детекторов зачастую настолько противоречат друг
другу, что извлечение информации о чарме представляет трудноразрешимую
задачу, если вообще возможно [3].
Точность измерений на подземных установках существенно ограничена
неопределенностями плотности и химического состава окружающего
установку грунта. Уместно поэтому, вспомнить такие важные
преимущества подводных черенковских установок, как высокая
степень однородности вещества–поглотителя (вода, лед) и большой
детекторный объем, и обсудить потенциальные возможности нейтринных
телескопов (AMANDA [4],
Байкальский НТ [5], NESTOR [6])
в контексте измерения вклада ПМ и исследования моделей рождения
чарма.
В данной работе обсуждаются
результаты расчетов потоков АМ на уровне моря и под водой,
в которых вклад ПМ учтен как в непертурбативных феноменологических
подходах – рекомбинационной кварк-партонной модели (РКПМ)
[3] и модели кварк-глюонных
струн (МКГС) [7],
так и в КХД-моделях [8].
Последние основаны на теории возмущения КХД и использовании
непертурбативных функций фрагментации на стадии адронизации
[9]. Недавние КХД
расчеты показали, что нелидирующие вклады O
(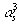 ),
связанные, главным образом, с процессами глюон–глюонного рассеяния
и рождения
),
связанные, главным образом, с процессами глюон–глюонного рассеяния
и рождения 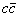 -пар
gg ®
-пар
gg ®
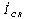 ,
дают фактор 2–2.5 в сечении рождения чарма. Предсказанные
в работе [8]
вертикальные потоки атмосферных ПМ на уровне моря начинают
доминировать при энергиях мюона от 200 ТэВ до 1
ПэВ, в зависимости
от выбора партонных распределений и параметров КХД-модели
– массы c-кварка
mc,
энергетической шкалы mR,
задающей ренормированный заряд as
~ 1/ln(mR/L),
и шкалы факторизации mF,
отделяющей пертурбативную динамику от инфракрасной области.
Представляет интерес сравнение результатов этих трех подходов,
а также исследование трансформации спектров АМ после прохождения
мюонами толстого слоя воды. На каких глубинах под водой, при
каких энергиях и под какими зенитными углами можно обнаружить
различие моделей и, в идеале, извлечь параметры КХД из данных
по мюонным потокам?
,
дают фактор 2–2.5 в сечении рождения чарма. Предсказанные
в работе [8]
вертикальные потоки атмосферных ПМ на уровне моря начинают
доминировать при энергиях мюона от 200 ТэВ до 1
ПэВ, в зависимости
от выбора партонных распределений и параметров КХД-модели
– массы c-кварка
mc,
энергетической шкалы mR,
задающей ренормированный заряд as
~ 1/ln(mR/L),
и шкалы факторизации mF,
отделяющей пертурбативную динамику от инфракрасной области.
Представляет интерес сравнение результатов этих трех подходов,
а также исследование трансформации спектров АМ после прохождения
мюонами толстого слоя воды. На каких глубинах под водой, при
каких энергиях и под какими зенитными углами можно обнаружить
различие моделей и, в идеале, извлечь параметры КХД из данных
по мюонным потокам?
2 Атмосферные мюоны на уровне моря
Расчет потоков (p,K)-мюонов и ПМ в МКГС и РКПМ на уровне моря под разными зенитными углами для энергий Em ³
1 ТэВ был выполнен на основе модели ядерного каскада [10], в которую внесен ряд уточнений [3, 11]. В качестве граничного использовался спектр первичных космических лучей С.И. Никольского [12]. Параметризации предсказаний КХД-моделей, полученных на уровне моря для направлений, близких к вертикали, взяты из работы [8].
Дифференциальные энергетические спектры
АМ на уровне моря (умноженные на 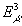 ),
вычисленные для вертикального и горизонтального направлений,
приведены на рис. 1
вместе с данными экспериментов [13,
14, 15, 16, 17, 18]. Все приведенные данные были получены
из обработки результатов подземных экспериментов, за исключением
данных спектрометра MUTRON [13].
),
вычисленные для вертикального и горизонтального направлений,
приведены на рис. 1
вместе с данными экспериментов [13,
14, 15, 16, 17, 18]. Все приведенные данные были получены
из обработки результатов подземных экспериментов, за исключением
данных спектрометра MUTRON [13].
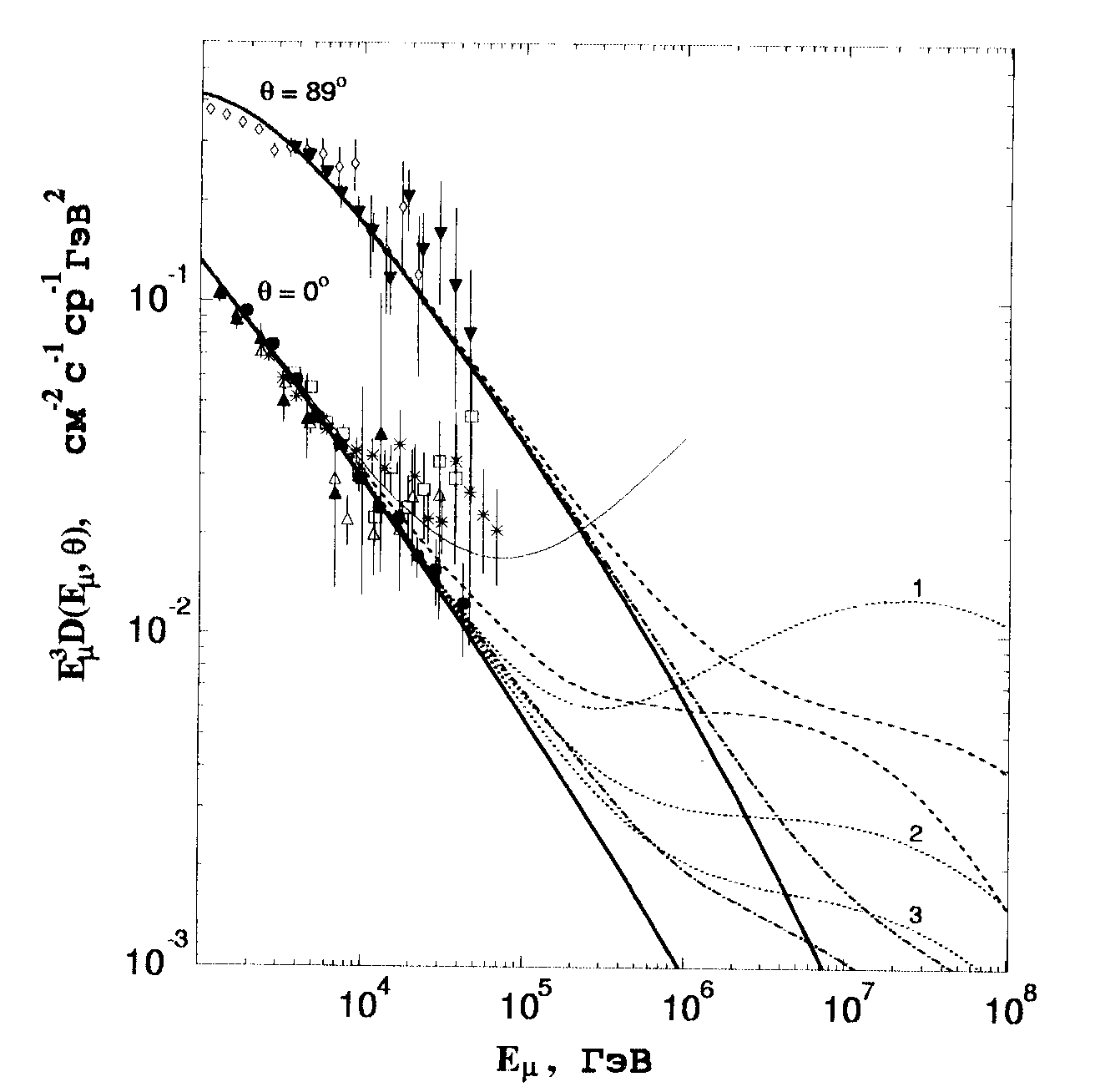
Вклад РКПМ раньше других моделей начинает менять показатель спектра АМ – при энергиях ~ 20 ТэВ на вертикали. Вклады в ПМ в рамках КХД-моделей (пунктирные линии на рис. 1) существенно зависят от набора используемых партонных распределений и масштабных параметров mF и mR: кривой 1 отвечает MRSD-набор с mF = 2mR = 2mc (mc = 1.3 ГэВ), кривым 2 и 3 – STEQ3-структурные функции с mF = 2mR = 2mc и mF = mR = mc соответственно [8]. Чтобы экспериментально обнаружить различие КХД-моделей, надо продвинуться на уровне моря до энергии ~ 100 ТэВ. Энергия Emc(J), при которой потоки удваиваются, для РКПМ равна приблизительно 150 TэВ (вертикаль), и ~ 1 ПэВ (89), что близко к предсказаниям КХД-1. Для МКГС значения Emc(J) » 850 ТэВ и 5 ПэВ близки к значениям, полученным в модели КХД-3.
|
|
Рис. 1. Вертикальные
и горизонтальные потоки мюонов еа уровне моря. Эксперимент:
à
-[13] (890),
и ▼ - [14], X –[15], ·
-[16], ▲ -[17], D
-[18]. Расчет:
сплошные линии – (p
,K
) –мюоны,
штриховые – с учетом ПМ РКПМ, штрихпунктир – МКГС,пунктир
(1, 2, 3) – предсказания КХД-моделей, верхняя тонкая
линия – ПМ [19].
|
Как видно из рис. 1, при Em > 10-20 ТэВ ни одна из обсуждаемых моделей не согласуется с данными РЭК МГУ [14] и детектора Frejus [15] и наоборот, ни одна из них не исключается данными LVD (Гран Сассо) [16]. (Измерения в Гран Сассо, по-видимому, закрывают фантастически высокие предсказания модели Волковой и др. [19].) Остальные экспериментальные данные, представленные на рис. 1, фактически не добавляют аргументов pro et contra. Эта парадоксальная ситуация ясно демонстрирует необходимость проведения новых экспериментов при существенно более высоких энергиях.
3 Потоки мюонов под водой
В качестве граничных спектров в задаче о прохождении мюонов через слой воды были взяты энергетические спектры мюонов и угловые распределения, рассмотренные в разделе 2. Задача была решена на основе аналитического метода, предложенного в работе [20]. Метод позволяет для граничного спектра, убывающего с энергией, приближенно решить кинетическое уравнение с интегралом столкновений, в котором учтена зависимость от энергии сечений взаимодействия мюона с веществом.
Не останавливаясь на деталях вычислений, приведем лишь одну характеристику, которая может представлять интерес для оценки потоков мюонов под толстым слоем воды или грунта на основе простых соотношений приближения непрерывных потерь. В табл. 1 приведена величина (как функция зенитного угла и глубины) отношения Rdc интегрального спектра при Em > 10 ГэВ, рассчитанного с дискретными потерями энергии, к спектру, полученному в приближении непрерывных потерь. Как видно из таблицы, эффект дискретных потерь для больших глубин не сводится просто к поправкам: Rdc ³
2.0 для слоя вещества толщиной ³
10 км в.э. Cама по себе угловая зависимость спектра мюонов моря мало влияет на эффект – главную роль здесь играет геометрический фактор secJ, определяющий толщину слоя воды x = h secJ (h–глубина по вертикали), поэтому, с точностью £
8 %, зависимость Rdc от x можно представить формулами:
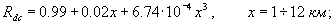
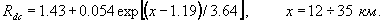
С ростом энергии эффект
дискретных потерь только усиливается. Зависимость Rdc
от 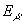 хорошо иллюстрируют следующие цифры: Rdc
хорошо иллюстрируют следующие цифры: Rdc
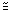 2.5 для
2.5 для 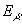 = 10 ГэВ и Rdc
= 10 ГэВ и Rdc
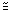 4.0
для
4.0
для 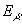 = 1 ТэВ на глубине 12 км в.э.
= 1 ТэВ на глубине 12 км в.э.
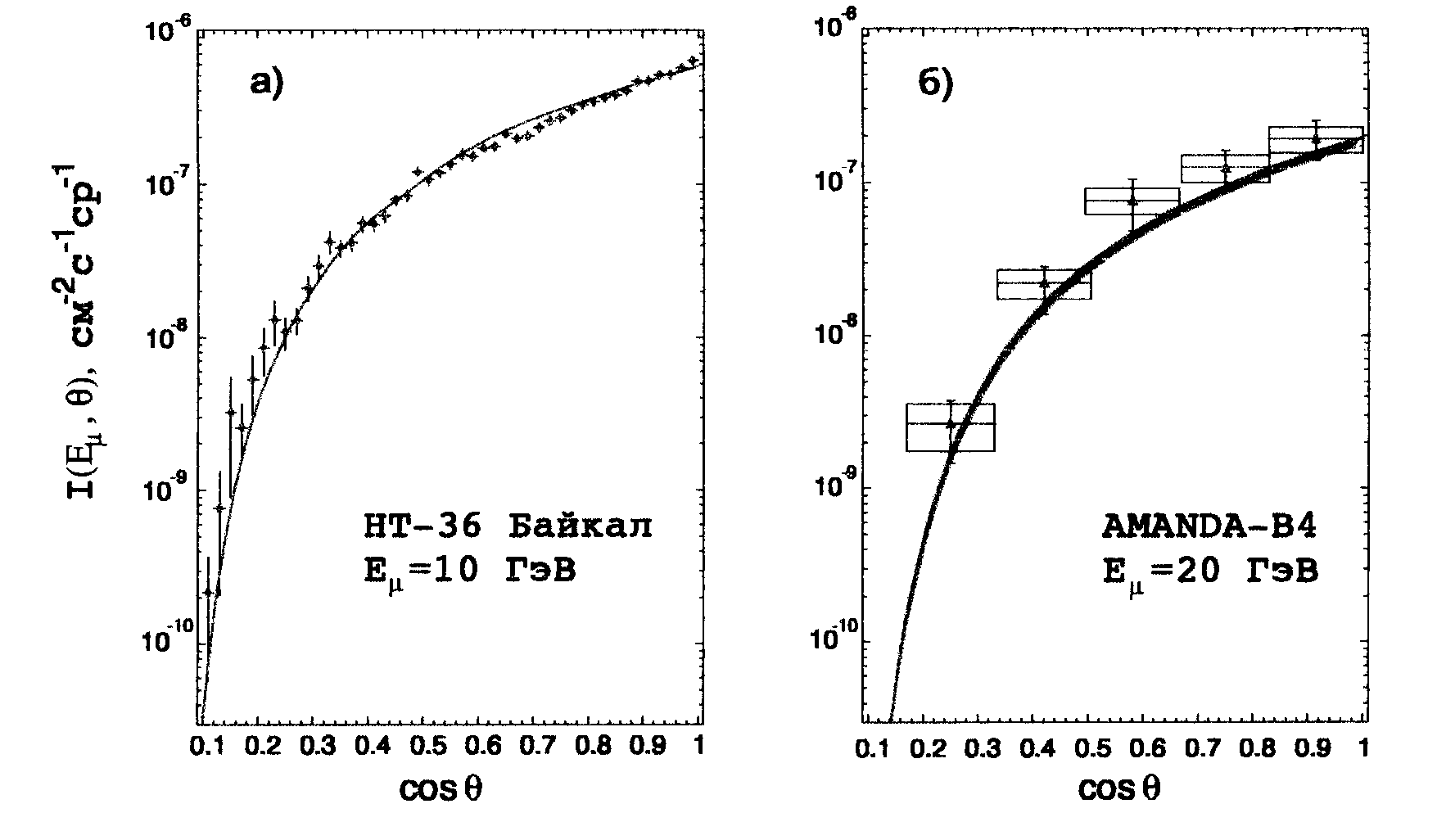
Данные измерений углового
распределения мюонов на двух нейтринных телескопах – НТ-36
[5] (а) и AMANDA [4] (б) в сравнении с расчетом (без учета
прямых мюонов) приведены на рис. 2. Кривая на рис. 2а рассчитана
для порога регистрации мюона 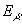 = 10 ГэВ на глубине h=1.17
км. В целом можно говорить об удовлетворительном согласии
расчетной кривой и эксперимента [5] для всех зенитных углов,
за исключением, быть может, интервала 80°
-84° .
Верхняя кривая на рис. 2б отвечает порогу
= 10 ГэВ на глубине h=1.17
км. В целом можно говорить об удовлетворительном согласии
расчетной кривой и эксперимента [5] для всех зенитных углов,
за исключением, быть может, интервала 80°
-84° .
Верхняя кривая на рис. 2б отвечает порогу 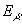 =0
ГэВ на глубине h=1.60
км в.э., нижняя – тому же порогу на глубине 1.68 км в.э. Область
больших углов здесь, в отличие от НТ-36, лучше согласуется
с расчетной кривой, чем интервал 45°
-60° .
=0
ГэВ на глубине h=1.60
км в.э., нижняя – тому же порогу на глубине 1.68 км в.э. Область
больших углов здесь, в отличие от НТ-36, лучше согласуется
с расчетной кривой, чем интервал 45°
-60° .
Таблица 1
Отношение
потока мюонов, рассчитанного с учетом дискретного характера
энергетических потерь, к потокам в приближении непрерывных
потерь 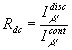
|
 град
град
|
sec 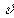
|
h, км в.э. |
|
1 |
2 |
3 |
4 |
|
0
60
70.53
75.52
78.46
80.40
81.79
82.82
83.62
84.26 |
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10. |
1.02
1.04
1.08
1.12
1.20
1.30
1.43
1.58
1.74
1.92 |
1.05
1.14
1.30
1.55
1.96
2.60
3.57
5.00
7.10
10.5 |
1.09
1.31
1.74
2.53
4.07
7.21
13.8
28.7
63.5
151 |
1.15
1.58
2.54
4.79
10.7
28.7
89.5
284
769
2320 |
|
|
|
Рис. 2. Данные нейтринных телескопов Байкал НТ-36 [5] (а), АМАНДА [4] (б) и зенитноугловое распределение, расчитанное для глубин h=1.15 и 1.60-1.68 км в.э. соответственно. |
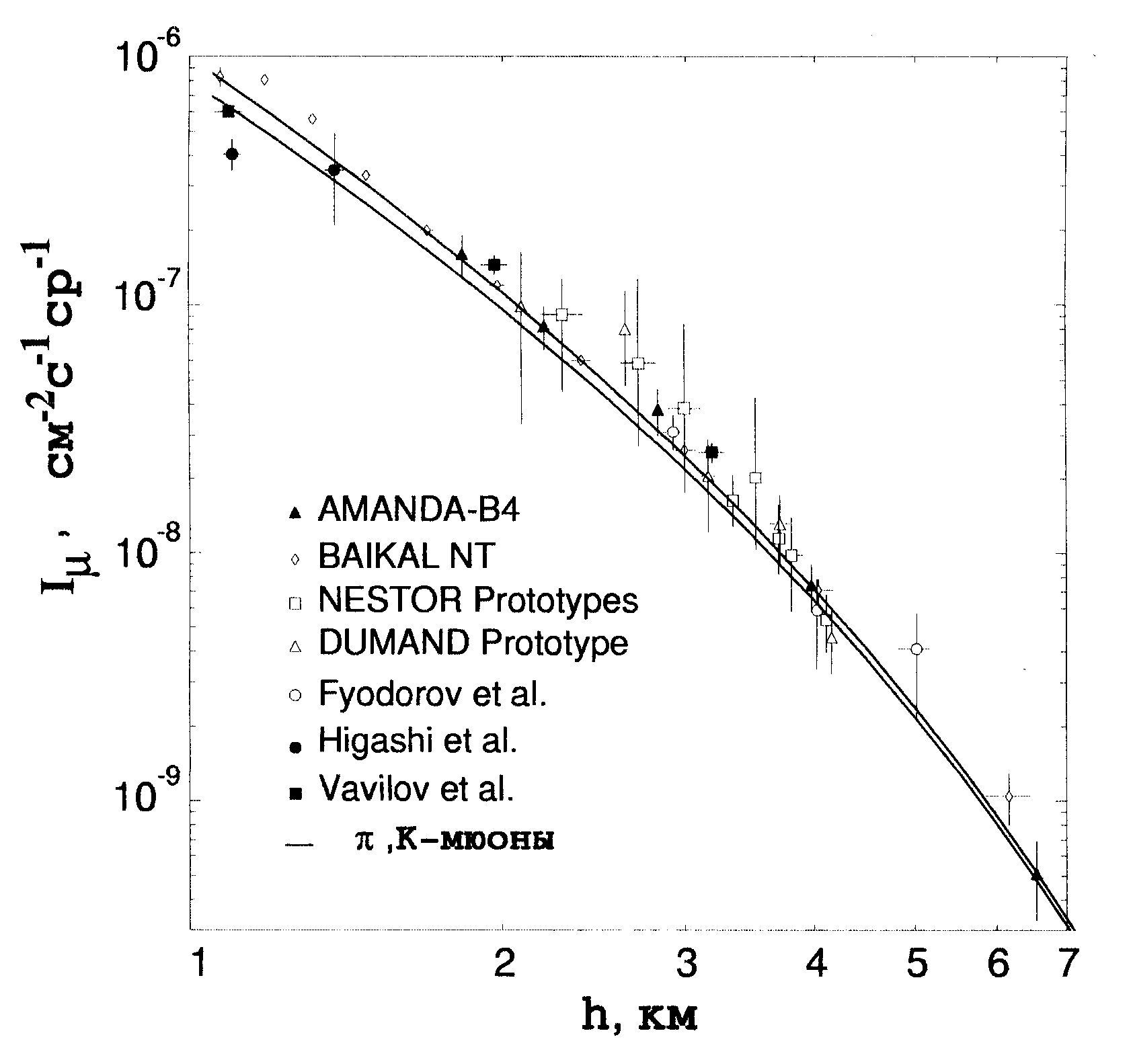
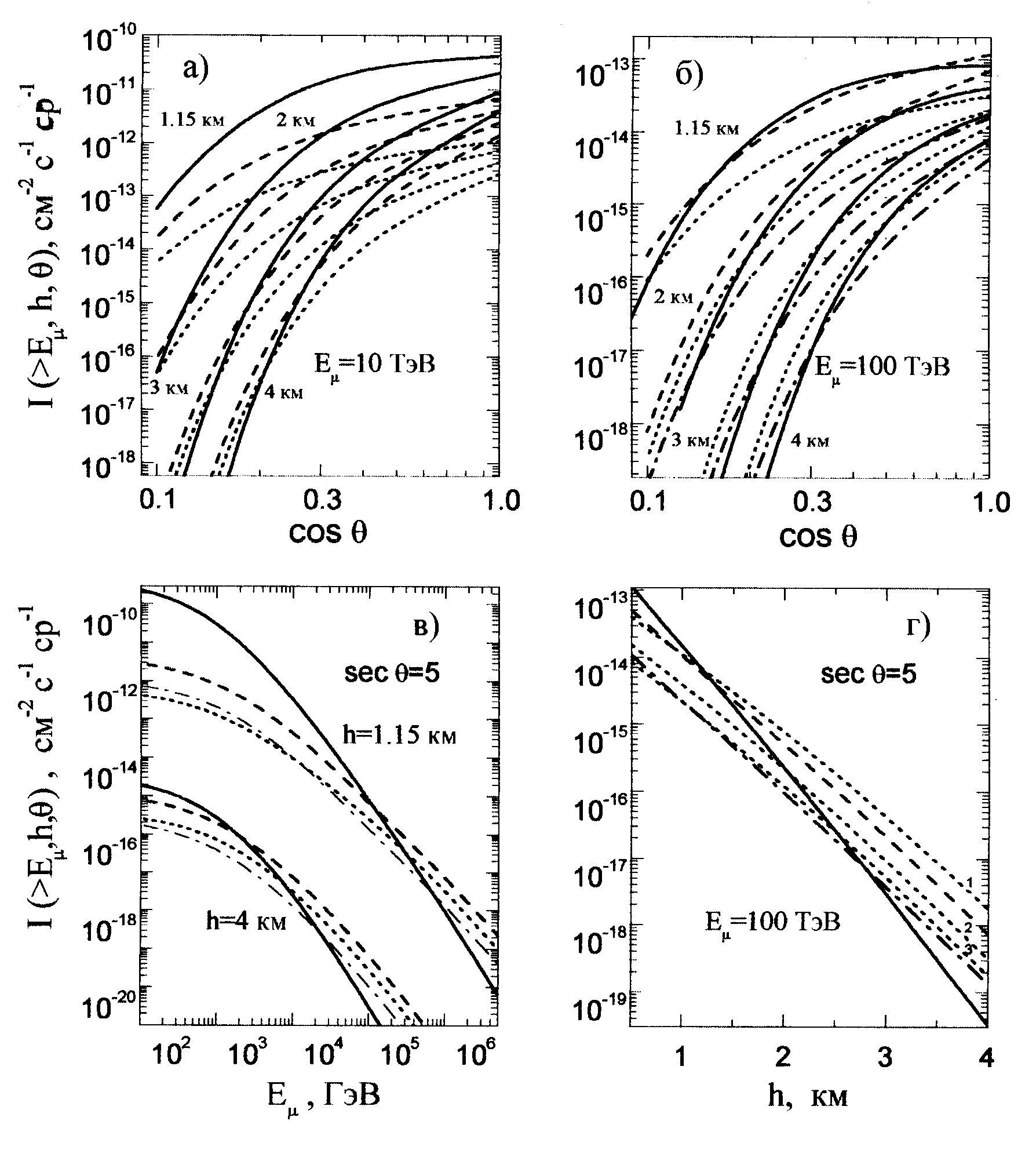
На рис. 3 приведено сравнение
рассчитанной кривой поглощения мюонов в воде с данными многолетних
подводных измерений (см. [3] и [5]), включая последние – полученные
на установке AMANDA [4]. Расчет представлен для двух значений
порога регистрации 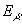 = 1 ГэВ и
= 1 ГэВ и 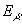 = 20 ГэВ (нижняя кривая). При
пороге регистрации
= 20 ГэВ (нижняя кривая). При
пороге регистрации 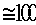 1 ТэВ рассчитывать на надежную идентификацию ПМ
при J
£ 80°
могут лишь телескопы, расположенные на глубинах 3-4 км (NESTOR).
Увеличение порога на порядок позволило бы как видно из рис.
4а, поставить такую задачу и на телескопе AMANDA (h
~ 2 км), но
при бóльших зенитных углах (J
³ 85°
). На установке
NESTOR порог
1 ТэВ рассчитывать на надежную идентификацию ПМ
при J
£ 80°
могут лишь телескопы, расположенные на глубинах 3-4 км (NESTOR).
Увеличение порога на порядок позволило бы как видно из рис.
4а, поставить такую задачу и на телескопе AMANDA (h
~ 2 км), но
при бóльших зенитных углах (J
³ 85°
). На установке
NESTOR порог 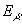 = 10 ТэВ позволяет перейти к меньшим углам и, следовательно,
увеличить статистику и уменьшить “фон” (p,
K)-мюонов. Высокий порог
= 10 ТэВ позволяет перейти к меньшим углам и, следовательно,
увеличить статистику и уменьшить “фон” (p,
K)-мюонов. Высокий порог 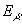 = 100 ТэВ (рис. 4б) дает возможность регистрации ПМ и на Байкальском
нейтринном телескопе (h
= 1.15 км).
= 100 ТэВ (рис. 4б) дает возможность регистрации ПМ и на Байкальском
нейтринном телескопе (h
= 1.15 км).
|
|
|
Рис. 3. Кривая
поглощения мюонов в воде. Точки – эксперимент: ·
-[21], -[22], o –[23], D
-[24], - [6], à -[5],
▲ -[4].
Кривые – расчет для Еm
>1 ГэВ
(верхняя иния) Еm >20
ГэВ.
|
Обратим внимание на поведение
кривой РКПМ на глубине 1.15 км (рис. 4б), дважды пересекающей
кривую (p,
K)-мюонов – при J 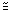 53°
и J
53°
и J
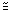 81° .
(На глубине 1.68 км подобное поведение замечено и для кривой
КХД-1). Появление такой особенности углового распределения
возможно на тех глубинах, где поток ПМ на вертикали чуть выше
потока обычных мюонов. Тогда доминирующий фактор углового
усиления (p,
K)-мюонов приводит к усилению степени "изотропности" потока
мюонов.
81° .
(На глубине 1.68 км подобное поведение замечено и для кривой
КХД-1). Появление такой особенности углового распределения
возможно на тех глубинах, где поток ПМ на вертикали чуть выше
потока обычных мюонов. Тогда доминирующий фактор углового
усиления (p,
K)-мюонов приводит к усилению степени "изотропности" потока
мюонов.
Принципиальная возможность
решения той же задачи, но уже из измерений интегральных спектров
для разных зенитных направлений показана на рис.4в. Здесь
представлены спектры мюонов на глубине h
= 1.15 км (Байкальский
НТ) и h
= 4 км (NESTOR) для зенитного угла J
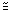 78.5°
(sec J =
5.0). Отдельно изображены предсказания трех моделей рождения
чарма (РКПМ, КХД-2, МКГС) и спектры (p,
K)-мюонов. Энергия
78.5°
(sec J =
5.0). Отдельно изображены предсказания трех моделей рождения
чарма (РКПМ, КХД-2, МКГС) и спектры (p,
K)-мюонов. Энергия 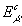 ,
при которой может наблюдаться удвоение потоков, существенно
ниже на глубине установки NESTOR по сравнению Байкалом (фактор
35–60 для sec J =
5.0). В частности, КХД-2 дает
,
при которой может наблюдаться удвоение потоков, существенно
ниже на глубине установки NESTOR по сравнению Байкалом (фактор
35–60 для sec J =
5.0). В частности, КХД-2 дает 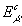 »
8 ТэВ для установки NESTOR, тогда как для Байкала
»
8 ТэВ для установки NESTOR, тогда как для Байкала 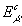 »
300 ТэВ. Тем не менее, поток мюонов c энергией вблизи
»
300 ТэВ. Тем не менее, поток мюонов c энергией вблизи 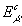 в Байкальской установке на порядок выше.
в Байкальской установке на порядок выше.
На рис.4г показаны вклады всех пяти рассмотренных моделей: РКПМ, МКГС и трех КХД-вариантов (цифры 1-3 у пунктирных кривых). Различие моделей на интервале глубин 1–3 км проявляется в диапазоне трех порядков величины потока мюонов. То, что абсолютная величина потока ПМ под “углом пересечения” модельно зависима, является обнадеживающим фактом для извлечения ограничений на КХД-параметры моделей рождения чарма из экспериментальных данных по угловым распределениям мюонов.
|
|
|
Рис. 4. Потоки мюонов на глубине 1-4 км под водой. Сплошные линии – потоки (p
, K
)-мюонов, остальные – ПМ в РКПМ (штриховые кривые), МКГС (штрих-пунктирные) и КХД (пунктирные). Рисунок (а) – зенитно-угловые распределения мюонов при Еm
³
10 ТэВ ; (б) – зенитно-угловые распределения мюонов при Еm
³
100 ТэВ; (в) – интегральные спектры для зенитного угла J
=78.46о (secJ
=5); (г) – зависимость потоков мюонов с энергиями Еm
³
100 ТэВ от вертикальной глубины для secJ
=5. |
4 Заключение
Вычисленные энергетические спектры и зенитно-угловые распределения атмосферных мюонов на уровне моря и под водой нa глубинах действующих и проектируемых нейтринных телескопов (1–4 км) и приведенные результаты сравнения расчета с данными НТ-36 [5] и эксперимента AMANDA-B4 [4], позволяют сделать следующие выводы:
1) предсказания максимальной пертурбативной КХД модели рождения чарма (КХД-1) в интересующем нас диапазоне энергий 10–100 ТэВ близки к результатам, полученным в рамках РКПМ, а минимальной, КХД-3, – практически совпадают с расчетом в рамках МКГС;
2) энергия, при которой доля прямых мюонов на уровне моря становится сопоставимой с обычными, (p, K)-мюонами, меняется в широком интервале: от 0.1 до 4 ПэВ, в зависимости от модели рождения чарма;
3) оценки вклада прямых
мюонов, сделанные на основе нескольких моделей рождения
чарма – МКГС, РКПМ и пертурбативных КХД-моделей, показывают,
что даже сравнительно небольшие глубины, как в месте расположения
НТ-200 (Байкал, h
~ 1 км), дают потенциальную возможность обнаружить прямые
мюоны – для не слишком больших зенитных углов (70°
-80°
), но при условии
увеличения порога регистрации до 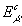 > 0.1 ПэВ;
> 0.1 ПэВ;
4) установка NESTOR
(Средиземное море, h
~ 4 км) c его большими глубинами позволяет иметь порог E
~ 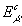 ~ 10 ТэВ (при sec J =
5.0), но при этом интенсивность потоков мюонов оказывается
на порядок меньше чем на НТ-200, где
~ 10 ТэВ (при sec J =
5.0), но при этом интенсивность потоков мюонов оказывается
на порядок меньше чем на НТ-200, где 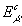 ~ 100 ТэВ.
~ 100 ТэВ.
Вообще говоря, “малоглубинные” (1-2 км) установки, при не слишком больших зенитных углах (J £
80°
), могут иметь определенные преимущества в будущих экспериментах с прямыми мюонами.
Что касается нейтринного телескопа AMANDA (Южный Полюс, h ~ 2 км), с которого сейчас начинают поступать мюонные данные, то здесь можно ожидать в ближайшее время продвижения до глубин, эквивалентных 18–20 км в.э. (J ³
84°
). И, следовательно, – решения проблемы прямых мюонов.
Авторы благодарят Drs. Christian Spiering и Stephan Hundertmark за любезно предоставленные таблицы данных по угловому распределению и кривой поглощения мюонов, полученных на установке AMANDA. Работа выполнена при финансовой поддержке Министерства образования РФ в рамках программы "Университеты России – фундаментальные исследования", грант № 728.
Литература
1. Hill G.C. // Astropart. Phys. 1997. 6. P. 215; Gaisser T.K., Halzen F., Stanev T. // Physics Repts. 1995. 258. P. 173; Barwick S., Halzen F., Lowder D. et al. // J.Phys. G: Nucl. Part. Phys. 1992. 18. P. 225; Nellen L., Manheim K. and Biermann P.L. Phys. Rev. 1993. D 47. P. 5270.
2. Bugaev E.V., Naumov V.A., Sinegovsky S.I., Zaslavskaya E.S. // Nuovo Cim. 1989. V. C12. P.41.
3. Bugaev E.V., Misaki A., Naumov V.A. et al.// Phys. Rev. 1998. V.D58. P.054001.
4. Andres E. et al. (AMANDA Collaboration). LANL astro-ph/9906203; Spiering Ch. (for the AMANDA Collaboration). LANL astro-ph/9906205.
5. Belolaptikov I.A. et al. (Baikal Collaboration).//Astropart. Phys. 1997. 7. P. 263.
6. Capone A. (for NESTOR Collaboration), Proc. of the 25th ICRC. Durban, South Africa. 1997. V. 7. P. 49; Anassontzis E. et al.(NESTOR Colaboration). В сб: ``Астрофизика и физика микромира. Материалы Байкальской школы по фундаментальной физике (11-17 октября 1998 г., Иркутск)''. Иркутск: изд-во Иркутского университета, 1998. C. 105.
7. Кайдалов А.Б., Пискунова О.И. // ЯФ. 1986. Т. 43. С.1545.
8. Pasquali L., Reno M.H., Sarcevic I. // Phys. Rev. 1999. V. D 59. P.034020.
9. Mangano M.L. Препринт CERN-TH/97-328, 1997. LANL hep-ph/9711337; Nason P., Dawson S. and Ellis R.K. // Nucl. Phys. 1988. V. B 303. P.607; // Nucl. Phys. 1989. V. B 327. P.49; Mangano M.L., Nason P., Ridolfi G. // Nucl. Phys. 1992. V. B 373. P.295.
10. Валл А.Н., Наумов В.А., Синеговский С.И. // ЯФ. 1986. Т. 44. С.1240.
11. Naumov V.A., Sinegovskaya T.S., Sinegovsky S.I.// Nuovo Cim. 1998. V. 111A. P.129.
12. Никольский С.И., Стаменов Й.И., Ушев С.З.// ЖЭТФ. 1984. Т. 87. С.18.
13. Matsuno S. et al.// Phys. Rev. 1984. V. D 29. P.1.
14. Зацепин Г.Т. и др. // Изв. РАН. Сер. Физ. 1994. Т. 58. С.119.
15. Rhode W.// Nucl. Phys. 1994. V. B 35. P.250.
16. Aglietta M. et al. // Phys. Rev. 1998. V. D 58. P. 092005.
17. Khalchukov F.F. et al. Proc. of the 19th ICRC, La Jolla, California,1985.V8 P12
18. Бакатанов В.Н. и др. // ЯФ. 1992. Т. 55. С.2107.
19. Volkova L.V. et al. // Nuovo Cim. 1987. V. 10 C. P.465.
20. Naumov V.A., Sinegovsky S.I., Bugaev E.V.// ЯФ. 1994. Т. 57. С.439.
21. Higashi S. et al.// Nuovo Cimento. 1966. 43 A. P.334.
22. Вавилов Ю.Н., Davitaev Л.Н., Трубкин Ю.А., Федоров В.М.// Известия АН СССР. Сер. Физ. 1970. Т. 2. С.1977.
- Fyodorov V.M.// Nucl. Instrum. and Methods. 1986. V. 248A. P.221.
Babson J. et al.(DUMAND Collaboration).// Phys. Rev. 1990. D 42. P. 3613.

