Z-ФАКТОРНЫЙ МЕТОД РЕШЕНИЯ ОДНОМЕРНЫХ УРАВНЕНИЙ ПЕРЕНОСА НУКЛОНОВ КОСМИЧЕСКИХ ЛУЧЕЙ В АТМОСФЕРЕ

В. А. Наумов, Т. С. Синеговская

Иркутский государственный университет

Предложен простой и эффективный метод решения уравнений переноса протонов и нейтронов космических лучей в атмосфере при высоких энергиях. Показано, что при учете нестепенного характера первичного спектра, роста полных неупругих сечений и нарушения скейлинга в нуклон-ядерных взаимодействиях, эффективные пробеги поглощения нуклонов сильно зависят не только от энергии, но и от глубины. Результаты расчетов сравниваются с имеющимися экспериментальными данными.

1 Введение.

Измерения потоков вторичных протонов и нейтронов космических лучей (КЛ) могут дать ценную информацию о первичном космическом излучении и о взаимодействиях нуклонов и ядер при высоких энергиях. Для извлечения этой информации из экспериментальных данных необходимо, помимо прочего, уметь вычислять пробеги поглощения нуклонов, являющиеся функционалами от спектра первичных КЛ, инклюзивных и полных неупругих сечений взаимодействия, а также, в общем случае, функциями энергии и глубины в атмосфере. Точное аналитическое решение этой задачи возможно лишь в рамках очень простых и, поэтому, далеких от реальности моделей первичного спектра и сечений взаимодействия. Между тем, быстрое развитие экспериментальной техники позволяет надеяться на качественное повышение точности измерений потоков как первичных, так и вторичных КЛ высоких энергий уже в ближайшем будущем, что требует разработки адекватных по точности расчетных методов. Кроме того, аккуратный расчет нуклонной компоненты вторичных КЛ является необходимым этапом расчета потока атмосферных нейтрино, – основного источника фоновых событий в астрофизических экспериментах на больших нейтринных телескопах и одного из важнейших "инструментов" исследования нейтринных осцилляций и других нестандартных эффектов физики электрослабых взаимодействий (см., например, [1]).

В данной работе предлагается простой и эффективный итерационный алгоритм приближенного решения одномерных уравнений переноса (УП) нуклонов КЛ, применимый при достаточно высоких энергиях без использования каких-либо нереалистичных предположений о форме первичного спектра, дифференциальных и полных сечений нуклон-ядерных взаимодействий. С некоторыми оговорками (см. раздел 2), решение УП может быть найдено с заданной точностью для произвольной глубины h, что позволяет изучать потоки нуклонов на уровне моря (у.м.) даже для наклонных направлений..

Основная идея метода заключается в сведении интегро-дифференциального УП к (нелинейному) интегральному уравнению для т.н. "Z-фактора", – величины непосредственно связанной с эффективным пробегом поглощения. Уравнение для Z-фактора решается затем простыми итерациями. Эффективность такого подхода уже была продемонстрирована в решении задачи переноса мюонных нейтрино в плотной среде с h>>l_n(E) [2] (l_n– пробег нейтрино до взаимодействия), т.е. в ситуации, где стандартные численные методы, включая метод Монте-Карло, либо неприменимы, либо требуют неприемлемо больших затрат машинного времени. С использованием ряда естественных физических приближений метод может быть легко модифицирован для решения задач переноса мезонов и мюонов высоких энергий в атмосфере и в плотных средах.

2 Основные приближения ядерно-каскадной модели.

Нас будут интересовать дифференциальные энергетические спектры протонов и нейтронов КЛ при энергиях достаточно высоких, чтобы можно было пренебречь энергетическими потерями протонов на ионизацию и возбуждение атомов воздуха, геомагнитными эффектами и эффектами 3-мерности каскадного процесса (в частности, рассеянием). Одномерное приближение (приближение "прямо-вперед") основано на сильной анизотропии в угловом распределении вторичных частиц, образующихся при неупругих взаимодействиях нуклонов и ядер и оправдано при импульсах нуклонов p >> á p_Tñ @ 0.4 ГэВ/c. Благодаря падающему характеру энергетического спектра КЛ (и, как следствие, преимущественной роли в развитии каскада процессов с p_T >> p_L), а также высокой степени изотропии первичного излучения, область применимости приближения "прямо-вперед" существенно расширяется для направлений близких к вертикальному [3]. В данной работе мы будем использовать стандартную модель суперпозиции для ядро-ядерных взаимодействий. Поскольку свободный пробег ядра быстро убывает с ростом атомного номера A, в этой модели считается, что ядра первичных КЛ с A>1 полностью фрагментируют в верхних слоях атмосферы и, следовательно, интегральный спектр ядер с энергиями і E_A можно аппроксимировать эквивалентным суммарным спектром Z протонов и A-Z нейтронов с энергиями E і E_A/A. При низких и промежуточных энергиях (в особенности, при энергиях меньших геомагнитного порога) такая модель оказывается слишком грубой и для расчета нуклонной компоненты необходимо применять более строгие подходы, учитывающие взаимодействия ядер КЛ явным образом [4]. При высоких энергиях применимость модели суперпозиции оправдывается в конечном счете (а) малостью соответствующего вклада в полных поток вторичных нуклонов и (б) отсутствием адекватных теоретических моделей взаимодействия ядер высоких энергий и достаточно детальных эмпирических данных.

Еще одно существенное приближение, которое будет использоваться ниже, заключается в пренебрежении процессами рождения N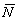-пар в мезон-ядерных взаимодействиях. На не слишком больших глубинах и (или) при небольших энергиях вклад в поток нуклонов, обусловленный этими процессами совершенно несуществен, поскольку (а) мезоны отсутствуют в первичном излучении и, следовательно, в верхних слоях атмосферы их поток мал по сравнению с потоком нуклонов, (б) дифференциальные сечения реакций pA ® KA ® 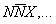малы по сравнению с сечениями реакций NA ® N'X и (в) лишь небольшая доля мезонов с E ≤ 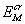(J) успевает провзаимодействовать с ядрами до распада. Однако, полные неупругие сечения NA-взаимодействий превышают сечения взаимодействий легких мезонов с ядрами (приблизительно на 30%). Поэтому при некоторой, достаточно большой глубине h=h_M(E,J) и при E > 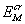(J) поток мезонов M становится равным потоку нуклонов тех же энергий. При h >> h_M(E,J) вкладом процессов генерации нуклонов в MA-взаимодействиях (в основном, – процессов p^± A ® N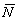X) пренебречь уже невозможно [5]. Таким образом, применимость излагаемого ниже формализма ограничена глубинами h ≤ h_p(E,J). В действительности, эта область оказывается довольно широкой.

В рамках перечисленных приближений задача вычисления дифференциальных энергетических спектров протонов D_p(E,h) и нейтронов D_n(E,h) на глубине h сводится к решению следующей системы одномерных УП:

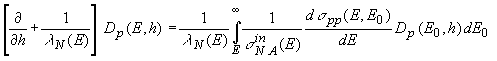
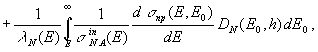(1)

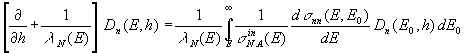
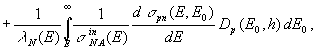(2)

с граничным условием (3)

где D_p⁰(E) и D_n⁰(E) – дифференциальные энергетические спектры протонов и нейтронов на "границе атмосферы", включающие (согласно модели суперпозиции) как первичные протоны, так и продукты фрагментации ядер КЛ.

В (1) и (2) использованы следующие обозначения: 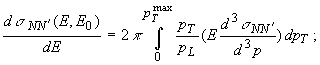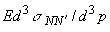– инвариантное дифференциальное сечение инклюзивной реакции N+A ® N'+X (где A – ядро атома воздуха, а X – система всех недетектируемых вторичных частиц, включая продукты развала ядра A); E₀ – полная энергия налетающего нуклона N; E – полная энергия, а p_T и p_L – составляющие импульса p конечного нуклона N'; l_N(E)=1/(N₀) – пробег нуклона до взаимодействия (где N₀ – число ядер A в 1 г воздуха). Величина 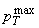определяется (в "NN-кинематике") условием 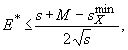где E^* – энергия инклюзивной частицы в системе центра масс сталкивающихся нуклонов, а 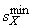– минимальное значение квадрата инвариантной массы системы X. В рамках NN-кинематики и в пренебрежении кумулятивной кинематической областью

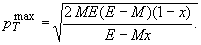
Здесь x=E/E₀ – доля энергии, уносимая нуклоном N', а M – масса нуклона.

Приближенная изотопическая симметрия NA-взаимодействий позволяет свести систему уравнений (1) и (2) к двум независимым уравнениям для линейных комбинаций

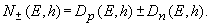
После простых преобразований, эти уравнения можно записать в виде

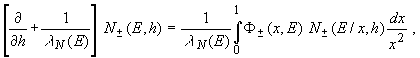(4)

где

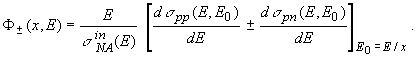
3 Z-факторный метод.

Введем определение эффективных пробегов поглощения L_±(E,h) с помощью соотношения 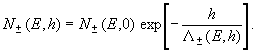(5)

Удобно ввести также вспомогательные безразмерные функции Z_±(E,h) ("Z-факторы"), следующим образом связанные с L_±(E,h) и l_N(E):

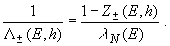(6)

Как и пробеги поглощения, Z-факторы содержат полную информацию о кинетике нуклонов в атмосфере. Непосредственно из УП (4) и определений (5) и (6) нетрудно увидеть, что 0 < Z₊(E,h) < 1. Функция Z_-(E,h), вообще говоря, не обязана быть знакоопределенной. Тем не менее, учитывая поведение реального первичного спектра КЛ и тот факт, что почти во всей кинематической области процессы регенерации (pA ® pX и nA ® nX) преобладают над процессами перезарядки (pA ® nX и nA ® pX), можно показать, что для нее тоже справедливы неравенства 0 < Z_-(E,h) < 1. Более того, легко доказать, что Z_-(E,h) < Z₊(E,h).

Подставляя (5) и (6) в УП (4), получаем уравнение на Z-факторы:

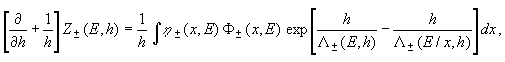(7)

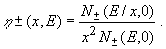где (8)

Поскольку во всем интересующем нас диапазоне энергий реальный первичный спектр убывает существенно быстрее, чем E^-2, то 0 Ј h_±(x,E) £ 1, причем h_±(0,E) = 0. В частности, для чисто степенного спектра ( ~ E^-g+1) имеем: h_±(x,E)=x^g-1. Интегрируя (7) по частям, приходим к следующему интегральному уравнению:

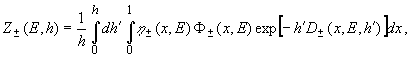(9)

где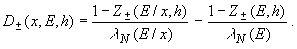

Хотя полученное уравнение нелинейно, оно гораздо удобнее для решения итерационным методом, чем исходное УП (4). Скорость сходимости итераций определяется выбором нулевого приближения. Простейшим выбором является 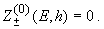При этом 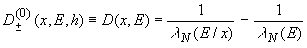(10)

не зависит от h и, в первом приближении, имеем:

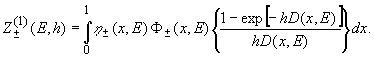(11)

Рассмотрим сперва случай небольших глубин. Учитывая, что область малых x в подынтегральном выражении (11) обрезается фактором h_±(x,E), можно формально разложить выражение в фигурных скобках по h. Это дает:

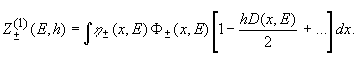(12)

Главный член разложения (12) 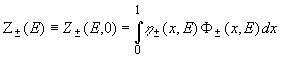(13)

совпадает с классической формулой Зацепина [6], которая была первоначально получена в рамках простейших предположений (степенной первичный спектр, скейлинг инвариантных инклюзивных сечений, независимость 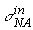от энергии) и до сих пор используется во многих аналитических расчетах ядерно-каскадных процессов в атмосфере. В противоположном предельном случае, учитывая известный рост 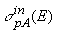с энергией, из (10) и (12) нетрудно увидеть, что 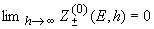. При весьма общих предположениях можно доказать также, что 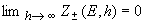и, следовательно, на достаточно больших глубинах пробеги поглощения L_±(E,h) совпадают со свободным пробегом l_N(E). Мы не будем останавливаться на доказательстве этого утверждения, т.к. уже по причинам, отмеченным выше (пренебрежение эффектами рассеяния, энергетическими потерями и вкладом нуклонов от мезон-ядерных взаимодействий) оно представляет лишь академический интерес. Важным является лишь тот факт, что с ростом глубины Z₊ и Z_- убывают, т.е. роль процессов регенерации уменьшается. С помощью формулы (12) можно воспроизвести приближенные аналитические результаты ряда работ, в которых учитывался (в рамках той или иной модели) рост 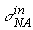с энергией (см., например, [5,7]).

Для n-ного приближения получаем рекуррентные соотношения (n > 0)

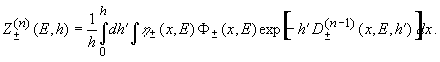(14)

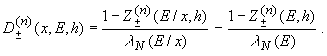(15)

Численный анализ показал, что даже при простейшем выборе Z_±⁽⁰⁾ = 0, скорость сходимости итерационного алгоритма (14–15) вполне достаточна для практического использования. Однако, как отмечалось выше, ее можно повысить более удачным выбором нулевого приближения. Например, учитывая неравенства 0 < Z_±(E,h) < 1, разумно положить 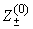(E,h)= Z_±(E)/2, что заметно улучшает сходимость в среднем.

4 Исходные данные и численные результаты.

4.1 Первичный спектр. Мы применяем параметризацию интегрального спектра первичных КЛ, предложенную Никольским, Стаменовым и Ушевым [8]. В этой модели ядерная компонента КЛ разделена на 5 стандартных групп ядер с = 1,4,15,26,51, спектры которых подобны при энергиях E_A << 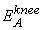и E_A >> 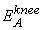, где 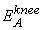характеризует область излома спектра для соответствующей группы. Значения параметров модели и явные формулы для эквивалентных дифференциальных спектров протонов и нейтронов приведены в [10,11]. В [10] дается также сопоставление модели Никольского-Стаменова-Ушева с экспериментальными данными по первичным КЛ, полученными до 1993 г.

Рассматриваемая модель не претендует на количественное описание первичного спектра при энергиях выше (10⁸-10⁹) ГэВ/нуклон. Однако вклад этой области энергий в статистику событий, представляющих интерес для экспериментов по измерению одиночной компоненты вторичных КЛ (включая эксперименты по глубоководной регистрации мюонов и нейтрино) несуществен. Поэтому, для упрощения расчетов, мы ввели искусственное "мягкое обрезание" первичного спектра, заменив функции 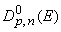в граничном условии (3) на 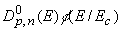, где 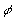(t) – некоторая безразмерная функция, удовлетворяющая условиям: 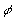(t) = 1 при t << 1 и 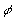(t) = 0 при t ³ 1. Явный вид этой функции не важен до тех пор, пока мы интересуемся энергиями E << E_c и не слишком большими глубинами h. Ниже полагаем E_c = 3 ´ 10¹⁰ ГэВ.

4.2 Сечения NA-взаимодействий.

Имеющиеся данные по полному неупругому сечению 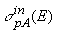(как ускорительные, так и извлеченные из экспериментов с космическими лучами) хорошо описываются эмпирической зависимостью

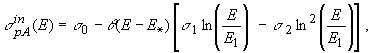(16)

где 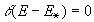при E < 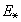и 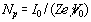при E і 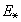, 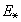= 45.4 ГэВ и E₁=1 ГэВ. Ниже мы используем формулу (16), со значениями параметров, найденными в [12]:

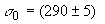мбарн, 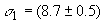мбарн, 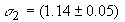мбарн.

Для инвариантных инклюзивных сечени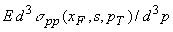й и 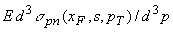мы приняли за основу (с минимальными модификациями) полуэмпирические формулы Кимеля-Мохова [13]. Свободные параметры в этих формулах были получены авторами фитированием всех доступных ускорительных данных по взаимодействиям нуклонов с различными ядерными мишенями при p₀ = 3 - 1500 ГэВ/c и 0.45 ГэВ/c £ p Ј p₀ (где p₀ – импульс налетающего нуклона в лабораторной системе).

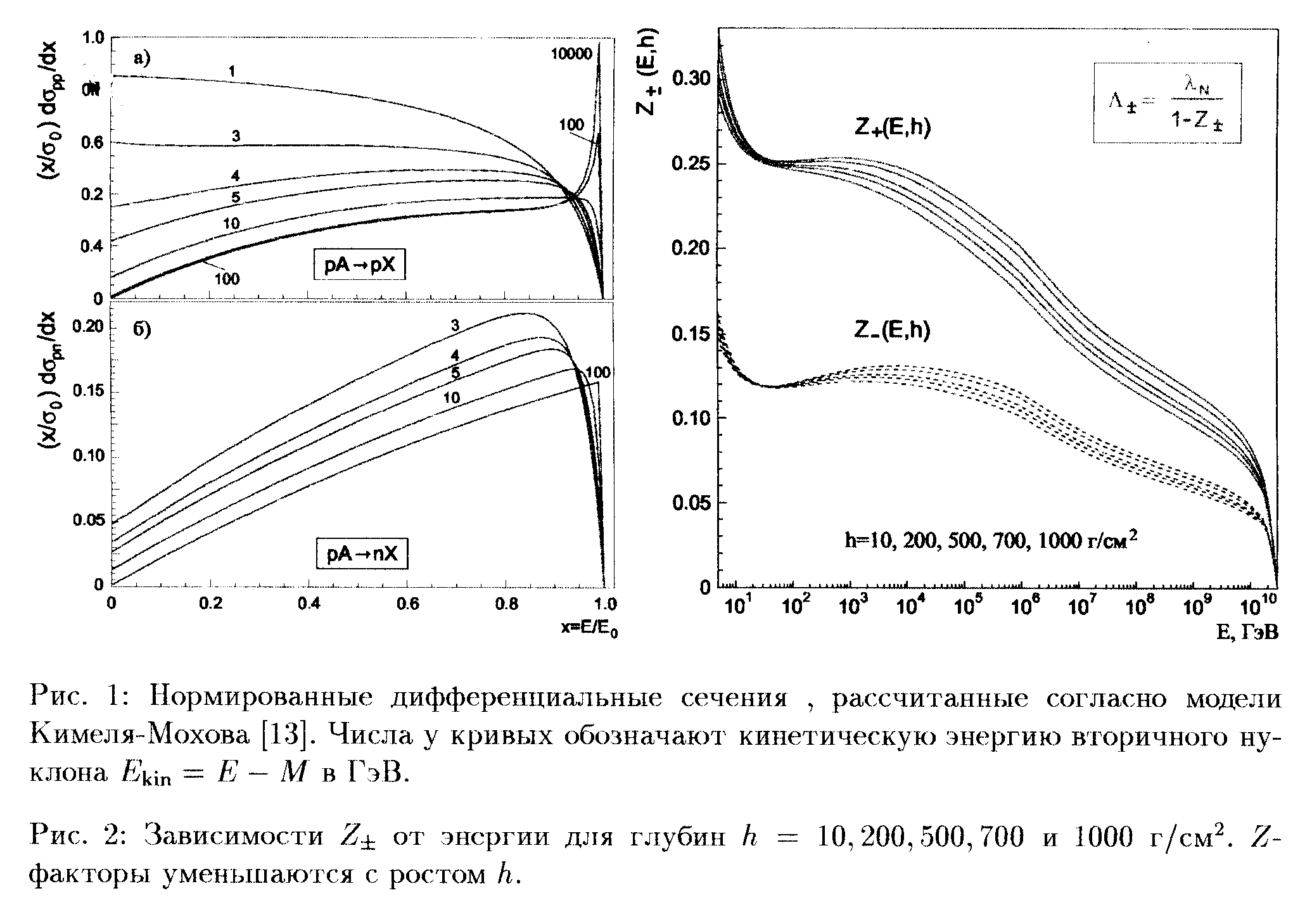
На рис. 1 показаны нормированные дифференциальные сечения 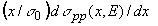и 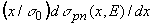, рассчитанные в модели Кимеля-Мохова для нескольких значений кинетической энергии вторичных нуклонов E_kin. Расчеты сделаны для бериллиевой мишени. Однако, дифференциальные сечения слабо зависят от атомного номера мишени, поэтому результаты справедливы и для других легких ядер, в частности, – для ядер атомов воздуха. Как видно из рисунка, при E_{kin ³} 100 ГэВ дифференциальные сечения практически перестают зависеть от энергии всюду, за исключением узкой дифракционной области для реакции pA ® pX. Другими словами, при высоких энергиях модель Кимеля-Мохова приводит к Фейнмановскому скейлингу. Из-за падающего характера первичного спектра вклад, который дифракционная область вносит в Z-факторы, отнюдь не пренебрежим. Чтобы избежать нефизически быстрого возрастания d в области x ~ 1 при сверхвысоких энергиях мы предположили, что при E₀ > 10⁶ ГэВ сечение d становится скейлинг-инвариантным во всей кинематической области. Из-за отсутствия экспериментальных данных при E₀ ³ 10⁶ ГэВ обосновать это предположение сегодня невозможно.

 

 

4.3 Результаты расчетов. Расчеты проводились для диапазонов 5 ГэВ Ј E Ј 3 ´ 10¹⁰ ГэВ и 0 Ј h Ј 5 ´ 10³ г/см². Для многомерного численного интегрирования применялся адаптивный кубатурный алгоритм Гинца-Мэйлика [14], а для аппроксимации и интерполяции промежуточных функций одной и двух переменных использовались стандартные локальные B-сплайны второй степени на равномерной сетке. При всех значениях E и h итерационный процесс быстро сходится. Так, 5–6 итераций оказывается достаточно для достижения точности расчета Z-факторов не хуже 10^-3-10^-4. На небольших глубинах, h £ 300 г/см², уже первое приближение обеспечивает точность на уровне нескольких процентов, вполне достаточную для многих приложений теории, например, для расчета потоков атмосферных мюонов и нейтрино.

На рис. 2 представлены зависимости Z-факторов от энергии для h=10, 200, 500, 700 и 1000 г/см². Наблюдаемая сильная зависимость Z_± от E и h вызвана тремя эффектами:

а) нестепенным поведением первичного спектра,

б) зависимостью полного неупругого сечения от энергией и

в) нарушением скейлинга.

Локальные минимумы, проявляющиеся при E < 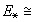45 ГэВ, обусловлены началом роста 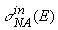(см. (16)). Заметное изменение характера энергетической зависимости при E ³ 10⁶ ГэВ связано с искусственным "замораживанием" роста квазиупругого пика в реакции pA ® pX. Наконец, обращение Z-факторов в нуль при E = E_c = 3 ´ 10¹⁰ ГэВ является следствием обрыва первичного спектра при E > E_c.

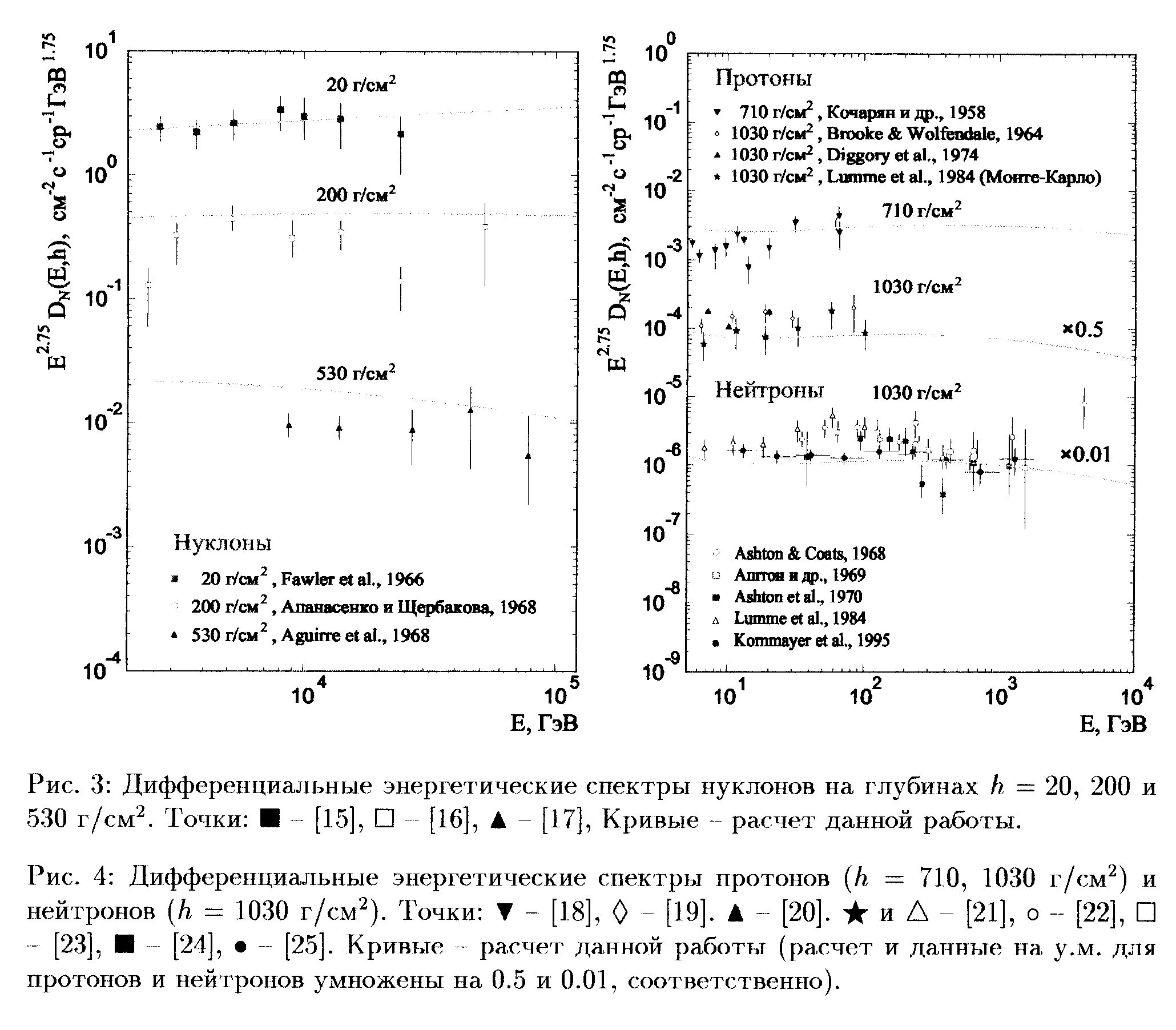
На рис. 3 и 4 дано сравнение расчетных дифференциальных энергетических спектров нуклонов (p + n), протонов и нейтронов на разных глубинах атмосферы с имеющимися экспериментальными данными [15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]. На рис. 4 приведены, кроме того, результаты расчета [21], выполненного методом Монте-Карло (для у.м.). Данные по спектрам нуклонов с E > 10³ ГэВ, относящиеся к глубинам h £ 530 г/см² (рис. 3), получены из анализа спектра g-квантов в широких атмосферных ливнях (см. [26]) и, поэтому, являются весьма модельно зависимыми. Тем не менее, наш расчет в целом не противоречит этой совокупности данных. Наибольшие разногласия наблюдаются с результатом работы [16]. По нашему мнению, оценка энергии нуклонов (по формуле 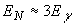), использованная в анализе [16], приводит к систематическому занижению интенсивности нуклонов. Прямые измерения спектров протонов на уровне гор и у.м. очень фрагментарны (рис. 4) и здесь можно говорить лишь о качественном согласии с расчетом. Экспериментальные данные по нейтронной компоненте на у.м., хотя и более представительны, но очень противоречивы. Наш расчет находится в неплохом согласии с недавними измерениями, выполненными на прототипе установки KASCADE в Карлсруэ [?].

Работа выполнена при финансовой поддержке Министерства образования РФ в рамках программы "Университеты России – фундаментальные исследования", грант № 728.

 

Литература

1. Koshiba M. // Phys. Rep. 1992. V. 220. P. 229. Gaisser T.K., Halzen F., Stanev T.// Phys. Rep. 1995. V. 258. P. 173; Erratum ibid. 1996. V. 271. P. 355. Наумов В.А. // В сб. "Астрофизика и физика микромира. Материалы Байкальской школы по фундаментальной физике". Под ред. В.А. Наумова, Ю.В. Парфенова и С.И. Синеговского. Иркутск, Изд-во ИГУ, 1998. C. 66.
2. Naumov V.A., Perrone L. // Astropart. Phys. 1999. V. 10. C. 239.
3. Battistoni G., Ferrari A., Lipari P., et al. // hep–ph/9907408. Tserkovnyak Y., Komar R., Nally C., Waltham C. // hep–ph/9907450.
4. Наумов В.А. // Исслед. по геомагнетизму, аэрономии и физике Солнца. М.: Наука, 1984. Вып. 69 (Теоретическая физика). С. 82. Бугаев Э.В., Наумов В.А. // ИЯИ АН СССР. Препринт П-0401. М., 1985. 32 c.
5. Валл А.Н., Наумов В.А., Синеговский С.И. // ЯФ. 1986. Т. 44. С. 1240.
6. Зацепин Г.Т. "Проблемы физики космических лучей". М.: Изд-во ИЯИ АН СССР, 1978. С. 189.
7. Григоров Р.Л. // ЯФ. 1977. Т. 25. С. 788. Волкова Л.В., Зацепин Г.Т., Кузьмичев Л.А. // ЯФ. 1979. Т. 29. С. 1252. Иваненко И.П., Роганова Т.М. "Каскадные ливни вызываемые частицами сверхвысоких энергий". М.: Наука, 1983. Bellandi J., Mundim L.M., Dias de Deus J., Covolan R.M.J. // J. Phys. G: Nucl. Phys. 1992. V. 18. P. 579.
8. Никольский С.И., Стаменов Й.И., Ушев С.З. // ЖЭТФ. 1984. Т. 87. C. 18. Никольский С.И. // В сб. "Проблемы физики космических лучей". Под ред. А.Е. Чудакова и др. М.: Наука, 1987. С. 169.
9. Greisen K. // Phys. Rev. Lett. 1966. V. 16. P. 748. Зацепин Г.Т., Кузьмин В.А. // Письма в ЖЭТФ. 1966. Т. 4. С. 114.
10. Bugaev E.V., Naumov V.A., Sinegovsky S.I., et al. // Proc. of the RIKEN International Workshop on Electromagnetic and Nuclear Cascade Phenomena in High and Extremely High Energies. Ed. M. Ishihara and A. Misaki. Tokyo, RIKEN, 1994. P 264.
11. Bugaev E.V., Misaki A., Naumov V.A., et al. // Phys. Rev. 1998. V. D 58 054001.
12. Mielke H.H, Foller M., Engler J., Knapp J.//J. Phys.G: Nucl. Part. Phys.1994 V20 P 637.
13. Кимель Л.Р., Мохов Н.В. // Изв. ВУЗов, физика. 1974. Вып. 10. C. 17. Кимель Л.Р., Мохов Н. В. // В сб. "Вопросы дозиметрии и защиты от излучений". М.: Атомиздат, 1975. Вып. 14. C. 41.
14. Genz A.C., Malik A.A. // J. Comput. Appl. Math. 1980. 6 295.
15. Fawler P. et al. // Nature. 1966. V. 209. P. 567.
16. Апанасенко А.В., Щербакова М.Н.//Изв. АН СССР, сер.физ. 1968 Т32. С.372, 374.
17. Aguirre C. et al. (Brazilian–Japaneze Emulsion Group)//Canadian J. of Phys. 1968 V46 P660
18. Кочарян Н.М., Саакян Г.С., Киракосян З.А. // ЖЭТФ. 1958. Т. 35. С. 1335.
19. Brooke G., Wolfendale A.W. // Proc. Phys. Soc. 1964. V. 84. P. 843.
20. Diggory I.S., Hook J.R., Jenkins I.A., Turver K.E. // J. Phys. A: Math., Nucl., Gen. 1974. V. 7. P. 741.
21. Lumme M., Nieminen M., Peltonen J., et al.//J. Phys.G: Nucl. Phys. 1984 V.10 P. 683.
22. Ashton F., Coats R.R. // J. Phys. A: Gen. Phys. 1968. V. 1 P. 169.
23. Аштон Ф., Кинг Дж., Мамиджанян Э.А., Смитт Н.И. // Изв. АН СССР, сер. физ. 1969. Т. 33. С. 1557.
24. Ashton F. Smith N.I, King J., Mamidzhanian E.A. // Acta Phys. Acad. Sci. Hung. 1970. V. 29 (Suppl. 3). P. 25.
25. Kornmayer H., Mielke H.H., Engler J., Knapp J. // J. Phys. G: Nucl. Part. Phys. 1995. V. 21. P. 439.

Григоров Н.Л., Рапопорт И.Д., Шестоперов В.Я., "Частицы высоких энергий в космических лучах". М.: Наука, 1973. 303c.