СЖАТИЕ И НАГРЕВ НЕСТАЦИОНАРНОЙ ПЛАЗМЕННОЙ СТРУИ СОБСТВЕННЫМ МАГНИТНЫМ ПОЛЕМ В ИМПУЛЬСНОМ ВАКУУМНОМ РАЗРЯДЕ
Е.В. Зверев
Институт солнечно-земной физики СО РАН, Иркутск
В последнее время проявляется повышенный интерес к исследованию физических процессов в плазме стационарного и импульсного вакуумно-дугового разряда [1]. Причиной этому служит интенсивное развитие следующих технических направлений: повышение эффективности вакуумных коммутаторов [2], использование вакуумно-дугового разряда в ионно-плазменных напылительных устройствах [3] и в источниках ионных пучков [4].
Плазма вакуумных дуг образуется при испарении вещества из небольших участков на поверхности катода, называемых катодными пятнами (размер 100 – 300 мкм, ток 30 – 300А). Они имеют сложную структуру и состоят из меньших по размеру фрагментов – эктонов или микропятен [5,6]. Их диаметр 1 – 3 мкм, ток 1 – 5 А, времена жизни – порядка 1нс. На расстояниях 30 – 50мкм потоки плазмы микропятен сливаются, образуя суммарную катодную плазменную струю (КПС) [12]. Основной нагрев, ускорение и ионизация плазмы происходят вблизи катода, на расстояниях порядка нескольких радиусов микропятна. В дальнейшем из-за падения плотности плазмы происходит "замораживание" зарядового состава. Ионы на больших расстояниях движутся практически с постоянной скоростью. Это объясняет тот факт, что в суммарных КПС стационарных дуг зарядовый состав ионов практически не зависит от тока дуги в диапазоне токов от единиц до нескольких сотен ампер [7].
Эксперименты по измерению
скорости ионов [8],
показали, что в плазме импульсных вакуумных разрядов появляются
ионы больших энергий, причем они наблюдаются лишь в импульсах
со скоростями роста тока 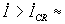 3×
108А/с,
и средняя энергия
3×
108А/с,
и средняя энергия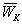 ионов растет при увеличении
ионов растет при увеличении 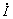 .
При более медленном нарастании тока значения
.
При более медленном нарастании тока значения 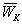 близки к стационарным (
близки к стационарным (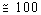 эВ).
По расчетам многих авторов, на плазменные струи вдали от катода
существенное влияние оказывает собственное магнитное поле
[10-12].
эВ).
По расчетам многих авторов, на плазменные струи вдали от катода
существенное влияние оказывает собственное магнитное поле
[10-12].
Таким, образом, теоретическое моделирование нестационарных КПС импульсных вакуумных разрядов представляет практический интерес. Для этой цели была получена квазиодномерная модель нестационарной плазменной струи с током. При таком подходе рассматривается изменение усредненных по сечению параметров плазмы, и свободной границы струи, форма которой определяется магнитным полем и средним плазменным давлением.
В качестве исходной использовалась
система одножидкостных уравнений магнитной гидродинамики. 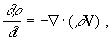 (1)
(1)
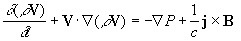 (2)
(2)
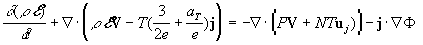 ,
(3)
,
(3)
дополненная законом Ома и уравнением Максвелла:
 ,
,
 .
(4,5)
.
(4,5)
Здесь
r ,
V, P, 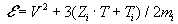 – плотность, направленная
скорость, давление и полная удельная энергия плазмы, N
и
T – концентрация
и температура электронов,
– плотность, направленная
скорость, давление и полная удельная энергия плазмы, N
и
T – концентрация
и температура электронов, 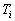 – ионная температура,
j и
– ионная температура,
j и 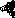 – плотность тока
и с проводимость, uj
– относительная
электронно-ионная (токовая) скорость, B
и
– плотность тока
и с проводимость, uj
– относительная
электронно-ионная (токовая) скорость, B
и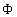 – магнитная индукция и электрический потенциал,
e – электрический
заряд, c
– скорость света,
– магнитная индукция и электрический потенциал,
e – электрический
заряд, c
– скорость света, 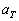 – коэффициент для
термосилы.
– коэффициент для
термосилы.
Инерция электронов,
теплопроводность и вязкости плазмы не учитывалась, ионы считались
холодными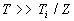 ,
их средний заряд считался постоянным
,
их средний заряд считался постоянным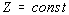 пренебрегалось [10].
Основные упрощающие предположения при
выводе одномерных уравнений – поперечная компонента скорости
плазмы по модулю значительно меньше радиальной, линии скорости
плазмы и плотности тока параллельны (образование токового
канала в замагниченной плазме) [12].
Постановка задачи была следующей: начальный ток и распределение
плазмы в промежутке соответствовали стационарной струе с током
пренебрегалось [10].
Основные упрощающие предположения при
выводе одномерных уравнений – поперечная компонента скорости
плазмы по модулю значительно меньше радиальной, линии скорости
плазмы и плотности тока параллельны (образование токового
канала в замагниченной плазме) [12].
Постановка задачи была следующей: начальный ток и распределение
плазмы в промежутке соответствовали стационарной струе с током
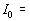 100
А [11].
В дальнейшем ток линейно
100
А [11].
В дальнейшем ток линейно 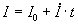 нарастал
во времени. Сечение и параметры плазмы на катодной границе
при этом оставались неизменными, за исключением концентрации,
которая росла пропорционально току. Иными словами, с увеличением
тока росло только число микропятен, а параметры струй отдельных
микропятен и ток на одно пятно не менялись. Расчет нестационарных
МГД – уравнений проводился методом крупных частиц
[14]. На противоположном
конце струи выбраны свободные граничные условия.
нарастал
во времени. Сечение и параметры плазмы на катодной границе
при этом оставались неизменными, за исключением концентрации,
которая росла пропорционально току. Иными словами, с увеличением
тока росло только число микропятен, а параметры струй отдельных
микропятен и ток на одно пятно не менялись. Расчет нестационарных
МГД – уравнений проводился методом крупных частиц
[14]. На противоположном
конце струи выбраны свободные граничные условия.
Обнаружено, что во всех
решениях наблюдалось сжатие и нагрев плазмы в струе, но в
расчетах со скоростью роста тока, превышающей некоторую пороговую
величину 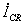 ,
характер сжатия начинает существенно изменяться. Сжатие сопровождается
образованием перетяжки (рис.1.), температура в которой достигает
довольно больших значений (30 – 80эВ). Происходит интенсивное
вытекание плазмы из перетяжки, со скоростью в несколько (2
– 3 для расчета на рис.1) раз выше стационарных значений.
,
характер сжатия начинает существенно изменяться. Сжатие сопровождается
образованием перетяжки (рис.1.), температура в которой достигает
довольно больших значений (30 – 80эВ). Происходит интенсивное
вытекание плазмы из перетяжки, со скоростью в несколько (2
– 3 для расчета на рис.1) раз выше стационарных значений.
В противоположном случае
(рис.2) "медленного" нарастания тока перетяжки не образуются,
а сжатие и повышение температуры менее значительно (5 – 15эВ),
и более равномерно по длине струи. Приблизительная граница
между двумя режимами – скорость нарастания тока 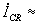 (5-10)×
108
А/с.
Физическая причина этого различия заключалась в следующем:
при "быстром" нарастании тока дополнительно образующаяся катодная
плазма не успевает распространиться по длине промежутка, и
происходит сжатие небольшой (начальной) массы струи. Как видно
из рис.1 (нижний
график), перетяжка образуется перед фронтом дополнительного
потока плазмы с катода.
(5-10)×
108
А/с.
Физическая причина этого различия заключалась в следующем:
при "быстром" нарастании тока дополнительно образующаяся катодная
плазма не успевает распространиться по длине промежутка, и
происходит сжатие небольшой (начальной) массы струи. Как видно
из рис.1 (нижний
график), перетяжка образуется перед фронтом дополнительного
потока плазмы с катода.
Во втором случае за
время сжатия струи поток плазмы распространяется практически
по всему промежутку, и сжатие происходит относительно равномерно.
Температура мало меняется по длине струи и пропорциональна
току, как и следует из условия равновесия, 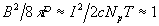 ,
где
,
где 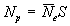 – число электронов на единицу длины (т.к. при медленном сжатии
– число электронов на единицу длины (т.к. при медленном сжатии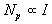 ).
Сечение струи
).
Сечение струи 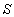 медленно увеличивается с расстоянием, вследствие компенсации
джоулева нагрева расширением.
медленно увеличивается с расстоянием, вследствие компенсации
джоулева нагрева расширением.
Появление ускоренных
ионов в расчетах наблюдается только в первом режиме. Этот
результат и величина 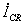 хорошо согласуются с экспериментом [8].
В решениях для "быстрого" сжатия получены существенные (до
200 – 300 В) неоднородности потенциала плазмы в перетяжках.
При достижении перетяжкой анодной границы, на ней появляются
аналогичные повышения потенциала. Такие всплески напряжения
довольно характерны для импульсных разрядов малой длительности
[9].
В [8] также
регистрировались скачки потенциала, совпадающие по времени
с появлением ускоренных ионов.
хорошо согласуются с экспериментом [8].
В решениях для "быстрого" сжатия получены существенные (до
200 – 300 В) неоднородности потенциала плазмы в перетяжках.
При достижении перетяжкой анодной границы, на ней появляются
аналогичные повышения потенциала. Такие всплески напряжения
довольно характерны для импульсных разрядов малой длительности
[9].
В [8] также
регистрировались скачки потенциала, совпадающие по времени
с появлением ускоренных ионов.
Поставленная задача применима
в основном к плазме вакуумной дуги, и результаты расчетов
приведены в соответствующих размерных переменных. Приведем
приближенную формулу для 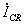 в общем виде. В [13] решалась
автомодельная задача о сжатии плазменного цилиндра в магнитном
поле нарастающего тока. Начальное плазменное давление считалось
малым. В этих условиях получались осциллирующие решения ,
время до начала первой осцилляции составляло
в общем виде. В [13] решалась
автомодельная задача о сжатии плазменного цилиндра в магнитном
поле нарастающего тока. Начальное плазменное давление считалось
малым. В этих условиях получались осциллирующие решения ,
время до начала первой осцилляции составляло  ,
где
,
где 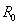 – начальный радиус,
– начальный радиус,  – масса на единицу длины, и ток
– масса на единицу длины, и ток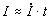 .
Образование перетяжек в нашей модели происходит, если
.
Образование перетяжек в нашей модели происходит, если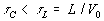 ,
где
,
где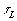 – время движения плазмы по промежутку длины
– время движения плазмы по промежутку длины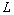 .
.
Подставим в формулу 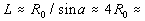 0,5см,
0,5см,
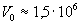 см/c,
см/c,
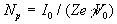 ,
где
,
где 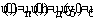 ,
,
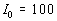 А.
Для катода из меди, средний ионный заряд
А.
Для катода из меди, средний ионный заряд 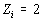 ,
и атомная масса
,
и атомная масса 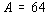 .
Граничная скорость нарастания тока при таких параметрах
.
Граничная скорость нарастания тока при таких параметрах 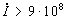 А/c.
Как видно, эта величина близка к полученной в наших расчетах
и к эксперименту [8].
А/c.
Как видно, эта величина близка к полученной в наших расчетах
и к эксперименту [8].
Литература.
- Вакуумные дуги. Под ред. Дж. Лафферти. М.: Мир, 1982, 432с.
- Раховский В.И. Физические основы коммутации электрического тока в вакууме. - М.: Наука, 1970, 536 с.
- Тез.докл. IV Всероссийской конф. "Модификация свойств конструкционных материалов пучками заряженных частиц". Томск 1996.
- Brown I.G. Vacuum arc ion sources. Rev. Sci. Instrum. 1994. V65. P.3061-3081.
- Месяц Г.А. Эктоны в вакуумной дуге .-Письма в ЖЭТФ. 1994.Т. 60. N6. С. 514-517.
- Jüttner B., Forster A. Evidence and consequences of cathode-spot substructure in vacuum arc. - IEEE Transl., XVth ISDEIV (1996) P.118-122.
- Kimblin C.W. Vacuum arc ion currents and electrode phenomena. - Proc. IEEE, 1971, v. 49, pp.546 -555.
- Gorbunov S.P., Krasov V.I., Paperny V.L. The acceleration of a cathode-jet plasma in a pulse vacuum discharge. Phys.D: Appl.Phys. 1997. V.30. P.2514-2518
- Алферов Д.Ф., Коробова Н.И. Сибиряк. И.О. Развитие сильноточного импульсного электрического разряда в вакууме. Физика плазмы.1993. T.19. N.3. с.399-410.
- Кринберг И.А., Луковникова М.П., Паперный В.Л. Стационарное расширение токонесущей плазмы в вакуум .ЖЭТФ. 1990. Т. 91. С. 806.
- Кринберг И.А., Зверев Е.А. Пространственная структура катодных плазменных струй в вакуумной дуге. Физика плазмы 1999. Т.25. в.1. с.88-95.
- Немчинский В.А. Расчет влияния аксиального магнитного поля на образование анодного пятна вакуумной дуги. ЖТФ. 1989. Т.59. В.9.С. 98-102.
- Леонтович М.А., Осовец С.М. О механизме сжатия тока при быстром и мощном газовом разряде. Атомная энергия. 1956. N. 3. 81-83.
Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. М.: Наука, 1982. 392 с.

