ПОТОКИ АТМОСФЕРНЫХ МЮОНОВ ВЫСОКИХ ЭНЕРГИЙ
Т. С. Синеговская
Иркутский государственный университет
Представлены
результаты расчета дифференциальных энергетических спектров
мюонов космических лучей при энергиях выше 1 ТэВ для различных
зенитных углов. В качестве дополнительных источников мюонов
рассматривались трехчастичные полулептонные распады заряженных
и нейтральных каонов и пионы от распадов тех же каонов. Учет
вкладов от 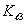 распадов и от пионов, рожденных в распадах каонов, приводит
к увеличению полных потоков мюонов на 3% и 2% соответственно.
Проведено детальное сравнение рассчитанных для уровня моря
спектров с экспериментом и с расчетами других авторов.
распадов и от пионов, рожденных в распадах каонов, приводит
к увеличению полных потоков мюонов на 3% и 2% соответственно.
Проведено детальное сравнение рассчитанных для уровня моря
спектров с экспериментом и с расчетами других авторов.
1. Введение Измерения спектров и зенитно-угловых распределений атмосферных мюонов дает возможность проверки моделей ядерного каскада в атмосфере, т.е. параметров первичного космического излучения (энергетический спектр, химический состав) и взаимодействий частиц при высоких энергиях. В частности, такие измерения могут дать информацию о механизмах рождения чарма в адрон-ядерных столкновениях, что представляет интерес для физики частиц и имеет важный прикладной аспект в нейтринной астрономии высоких энергий, поскольку атмосферные нейтрино от распада очарованных частиц являются основным источником фона при детектировании нейтрино внеземного происхождения (например, квазидиффузного потока нейтрино от активных галактических ядер).
Улучшение точности в расчетах измеряемых характеристик атмосферного потока нейтрино становится необходимым для ведущихся и планируемых экспериментов на подземных и глубоководных нейтринных телескопах. Для однозначной интерпретации современных данных по "upgoing muons" (т.е. мюонам, рожденным атмосферными нейтрино, идущими снизу вверх) поток нейтрино должен быть рассчитан по крайней мере с 10% точностью. Вследствие этого, возникает необходимость нормировки расчетного (модельно-зависимого) потока атмосферных нейтрино. Поток мюонов, рожденных в атмосфере в тех же процессах, что и нейтрино, является естественным инструментом для проверки и нормировки рассчитанных спектров нейтрино.
В данной
работе представлены результаты расчетов дифференциальных энергетических
спектров мюонов от распадов 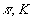 -мезонов
для различных зенитных углов в интервале энергий 1-100 ТэВ
и приведено сравнение с имеющимися экспериментальными данными.
Выше 100 ТэВ начинают доминировать мюоны от распадов очарованных
адронов (прямые мюоны), которые здесь подробно обсуждаться
не будут (см. [1, 2]).
-мезонов
для различных зенитных углов в интервале энергий 1-100 ТэВ
и приведено сравнение с имеющимися экспериментальными данными.
Выше 100 ТэВ начинают доминировать мюоны от распадов очарованных
адронов (прямые мюоны), которые здесь подробно обсуждаться
не будут (см. [1, 2]).
2. Адронный каскад при высоких энергиях
Расчет
потоков атмосферных мюонов на уровне моря под разными зенитными
углами для энергий 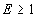 ТэВ
выполнен на основе модели ядерного каскада [3], которая хорошо
описывает имеющиеся экспериментальные данные по спектрам адронов
на различных глубинах при энергиях от 1 Тэв до 600 ТэВ. Основные
положения модели [3] сводятся к следующему.
ТэВ
выполнен на основе модели ядерного каскада [3], которая хорошо
описывает имеющиеся экспериментальные данные по спектрам адронов
на различных глубинах при энергиях от 1 Тэв до 600 ТэВ. Основные
положения модели [3] сводятся к следующему.
- На стадии развития
адронного каскада (но, разумеется, не на стадии генерации
лептонов) распад пиона можно не учитывать при энергиях
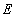 ”
”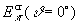 ≈
0.12 ТэВ, т. е. начиная с
≈
0.12 ТэВ, т. е. начиная с 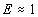 ТэВ на вертикали.
ТэВ на вертикали.
- Ядра первичных космических лучей фрагментируют в верхних слоях атмосферы, так как их пробеги взаимодействия существенно меньше пробега нуклона. Это позволяет использовать для ядерной компоненты модель суперпозиций.
- Для инвариантных инклюзивных
сечений
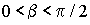 предполагается справе-дливость фейнмановского скейлинга
исходя из отсутствия экспериментальных данных и серьезных
теоретических указаний о его нарушении во фрагментационной
области (в области пионизации нарушение скейлинга не оказывает
большое влиян-ия на развитие каскада, так как область малых
фейнмановских
предполагается справе-дливость фейнмановского скейлинга
исходя из отсутствия экспериментальных данных и серьезных
теоретических указаний о его нарушении во фрагментационной
области (в области пионизации нарушение скейлинга не оказывает
большое влиян-ия на развитие каскада, так как область малых
фейнмановских 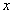 (Í 0.1)
подавлена быстро падающим первичным спектром).
(Í 0.1)
подавлена быстро падающим первичным спектром).
- Для полных неупругих
сечений взаимодействия адрона
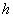 на ядерной мишени
на ядерной мишени 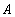 предполагается логарифмический рост с энергией
предполагается логарифмический рост с энергией 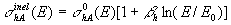 где параметр наклона
где параметр наклона 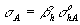 не зависит от сорта адрона.
не зависит от сорта адрона.
- Процессы генерации пионов и нуклонов в каон-ядерных столкновениях и реге-нерации каонов не учитываются.
В качестве
спектра первичных космических лучей взят спектр Никольского
[4]. Приближенное решение системы кинетических уравнений переноса
нуклонов и мезонов в атмосфере, основываясь на вышеперечисленных
допущениях, может быть найдено в виде разложений по степеням
безразмерного параметра 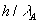 ,
где
,
где 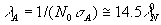 .
Этим решением, как показано в [3], можно пользоваться до глубин
.
Этим решением, как показано в [3], можно пользоваться до глубин
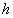 <
500 -600 г/см2.
Для
<
500 -600 г/см2.
Для 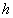 Ê
600 г/см2
следует учесть поправки
на глубину (O
Ê
600 г/см2
следует учесть поправки
на глубину (O 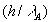 ).
Эти поправки не сказываются заметно на потоках мюонов, поскольку
большая часть мюонов генерируется на глубинах
).
Эти поправки не сказываются заметно на потоках мюонов, поскольку
большая часть мюонов генерируется на глубинах 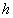 Í
300 г/см2.
Однако, они становятся существенными для расчета потоков адронов
на уровне моря.
Í
300 г/см2.
Однако, они становятся существенными для расчета потоков адронов
на уровне моря.
3. Спектры мюонов на уровне моря
Основными
каналами генерации мюонов для энергий 1-100 ТэВ являются двухчастичные
распады пионов и каонов. В качестве источников мюонов дополнительно
рассматривались трехчастичные полулептонные распады заряженных
и нейтральных каонов 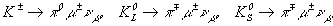 и пионы от распадов
тех же каонов
и пионы от распадов
тех же каонов 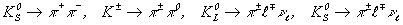 .
.
Учет
этих вкладов приводит к увеличению полных потоков мюонов на
~ 3% от полулептонных распадов и на ~ 2% от пионов, рожденных
в распадах каонов. Был учтен также такой тонкий эффект, как
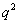 -зависимость
форм-факторов трехчастичных полулептонных мод распада каона
[5]. Эффект практически не сказывается на величине суммарного
(полного) потока мюонов: он мал для мюонов от
-зависимость
форм-факторов трехчастичных полулептонных мод распада каона
[5]. Эффект практически не сказывается на величине суммарного
(полного) потока мюонов: он мал для мюонов от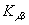 распада, а цепочка распадов
распада, а цепочка распадов 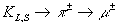 (для которой
(для которой 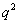 -зависимость
приводит к уменьшению спектров мюонов на ~8 %) дает поправку
менее процента. Однако эффект форм-факторов не пренебрежим
для атмосферных нейтрино высоких энергий [6] и, следовательно,
его следует учесть и в расчете потока мюонов (который предполагается
использовать для нормировки нейтринного потока).
-зависимость
приводит к уменьшению спектров мюонов на ~8 %) дает поправку
менее процента. Однако эффект форм-факторов не пренебрежим
для атмосферных нейтрино высоких энергий [6] и, следовательно,
его следует учесть и в расчете потока мюонов (который предполагается
использовать для нормировки нейтринного потока).
Расчет
потоков атмосферных мюонов на уровне моря под разными зенитными
углами был выполнен в стандартном приближении непрерывных
энергетических потерь. Сравнение рассчитанных дифференциальных
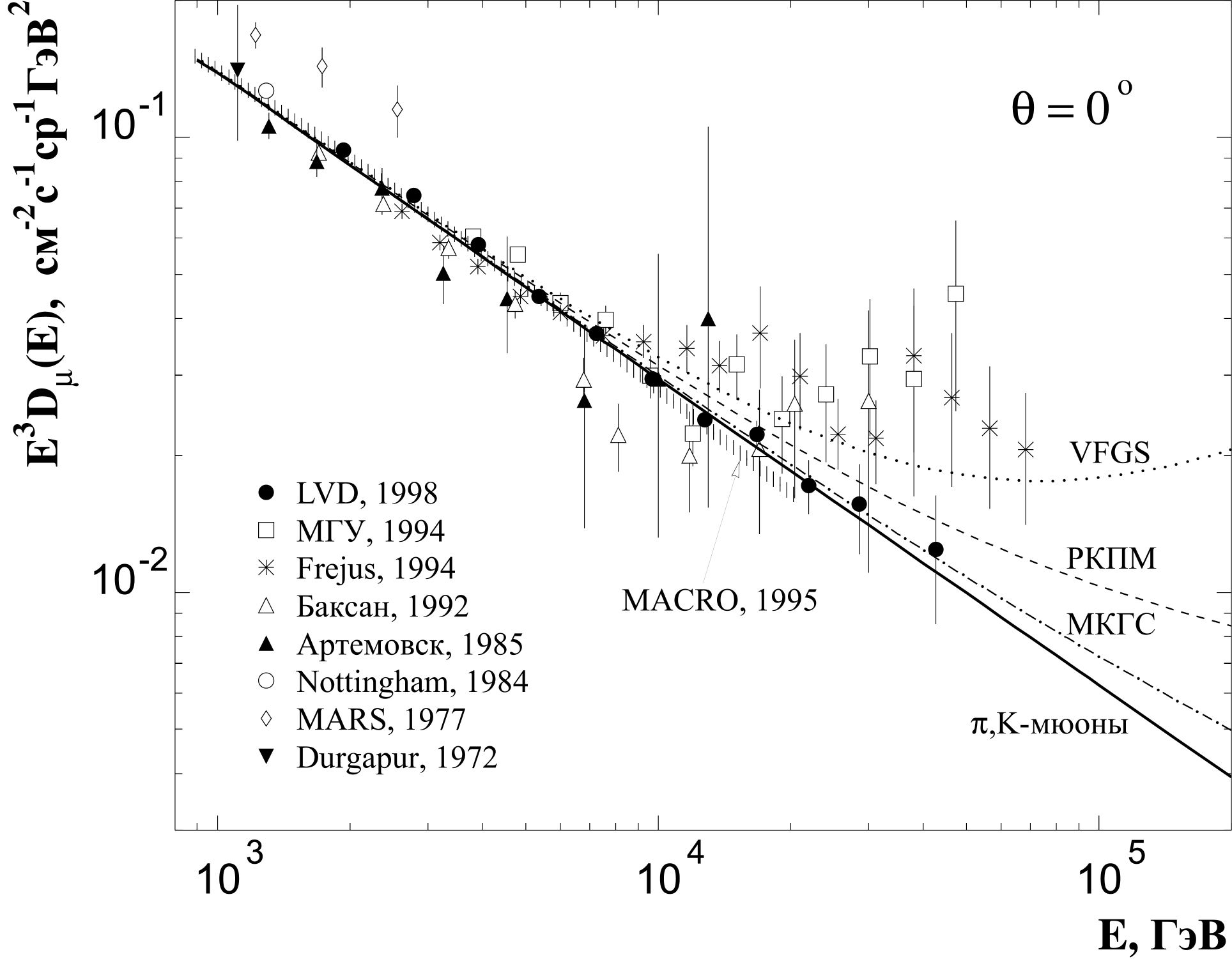
энергетических спектров мюонов (от 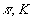 -мезонов)
для различных зенитных углов сэкспериментальными данными со
спектрометров и подземных установок приведено на рисунках
1-3.
-мезонов)
для различных зенитных углов сэкспериментальными данными со
спектрометров и подземных установок приведено на рисунках
1-3.
Имеющиеся экспериментальные данные можно (несколько условно) разделить на прямые и косвенные. К прямым относятся данные измерений на магнитных спектрометрах Дургапура [7], Ноттингема [8], Дарема [9], MUTRON [10], DEIS [11], Брукхевена [12] и электромагнитных калориметров [13]. Косвенные данные, т. е. данные, пересчитанные разными методами к уровню моря из результатов подземных измерений (в частности, из кривой поглощения мюонов в грунте), включают в себя измерения на сцинтилляционном детекторе ИЯИ в Артёмовске [14], рентгено-эмульсионных камерах МГУ [15, 16], Баксанском подземном сцинтилляционном телескопе [17], детекторах Frejus [18], MACRO [19] и LVD [20].
|
|
|
Рис.
1. Дифференциальные спектры мюонов на уровне моря для
вертикали. Эксперимент: ·
- [20], - [15], *
- [18], D - [17], ▲
- [14], ° - [8], à
- [9], ▼ - [7].
Расчет: сплошные линии - (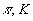 )-мюоны,
штриховые - с учетом ПМ РКПМ, штрих-пунктир - МКГС,
пунктир - предсказание модели Волковой и др. )-мюоны,
штриховые - с учетом ПМ РКПМ, штрих-пунктир - МКГС,
пунктир - предсказание модели Волковой и др.
|
Для энергий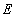 Í
2 ТэВ (вертикаль)
и E Í 20 ТэВ (
Í
2 ТэВ (вертикаль)
и E Í 20 ТэВ (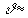 89°
) энергетический
спектр неплохо согласуется с прямыми измерениями. Для энергий
выше нескольких десятков ТэВ мы имеем в основном косвенные
данные подземных детекторов, и неопределенности
(как статистические, так и систематические) здесь значительно
выше, чем для прямых измерений, поскольку точность
подземных измерений
существенно ограничена неопределенностями
плотности и химического
состава окружающего установку грунта.
89°
) энергетический
спектр неплохо согласуется с прямыми измерениями. Для энергий
выше нескольких десятков ТэВ мы имеем в основном косвенные
данные подземных детекторов, и неопределенности
(как статистические, так и систематические) здесь значительно
выше, чем для прямых измерений, поскольку точность
подземных измерений
существенно ограничена неопределенностями
плотности и химического
состава окружающего установку грунта.
Для
направлений близких к горизонтальному, вклад прямых мюонов
предположительно незначителен при энергиях, доступных в текущих
экспериментах (MUTRON, DEIS, РЭК МГУ и др.). Поэтому при сопоставлении
экспериментальных данных с рассчитанным энергетическим спектром
мюонов с учетом мюонов от распада чарма ограничимся только
вертикальным направлением. Сплошной линией на рис.1 изображен
вклад от 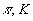 -мезонов,
штриховой, штрих-пунктирной и пунктирной линиями показаны
вклады прямых мюонов для трёх моделей рождения чарма: рекомбинационной
кварк-партонной модели (РКПМ), модели кварк-глюонных струн
(МКГС) [1] и эмпирической модели Волковой и др.[21], соответственно.
Хотя обсуждение моделей рождения чарма не является целью данной
работы, необходимо отметить, что расчеты потоков в рамках
РКПМ близки к максимальным предсказаниям недавней модели [22],
основанной на пертурбативной КХД, а расчеты, выполненные в
рамках МКГС, практически совпадают с минимальным предсказанием
этой модели (см. детали в работе [2]).
-мезонов,
штриховой, штрих-пунктирной и пунктирной линиями показаны
вклады прямых мюонов для трёх моделей рождения чарма: рекомбинационной
кварк-партонной модели (РКПМ), модели кварк-глюонных струн
(МКГС) [1] и эмпирической модели Волковой и др.[21], соответственно.
Хотя обсуждение моделей рождения чарма не является целью данной
работы, необходимо отметить, что расчеты потоков в рамках
РКПМ близки к максимальным предсказаниям недавней модели [22],
основанной на пертурбативной КХД, а расчеты, выполненные в
рамках МКГС, практически совпадают с минимальным предсказанием
этой модели (см. детали в работе [2]).
|
|
|
Рис. 2. Дифференциальные энергетические спектры мюонов на уровне моря для зенитных углов 45°
, 72°
и 89°
. |
Максимальные
потоки, которые дает РКПМ в этой области энергий, только с
некоторой натяжкой можно считать не противоречащими данным
РЭК МГУ [15] и Frejus [18].Предсказания же МКГС скорее не
подтверждаются этой группой экспериментальных данных, в отличие
от данных LVD из Гран Сассо [20]. Вероятно можно говорить
о некотором противоречии данных МГУ (для вертикали) и установки
Frejus (и, в какой-то степени, Артёмовска [14] и Баксана [17]),
c одной стороны, и эксперимента на подземной установке LVD
- с другой. Для данных LVD (тёмные кружочки на рис.1 характерна
высокая степень согласованности (с точки зрения нашего расчета)
спектра, пересчитанного к уровню моря, и кривой поглощения
мюонов, измеренной непосредственно на подземной установке.
Т. е. данные LVD и на глубине 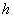 ~106
г/см2
требуют минимального вклада ПМ (см. рис.14 в [1]), совместимого
с предсказаниями МКГС (хотя, они не противоречат РКПМ). Измерения
в Гран Сассо, по-видимому, закрывают предсказания модели Волковой
и др. [21].
~106
г/см2
требуют минимального вклада ПМ (см. рис.14 в [1]), совместимого
с предсказаниями МКГС (хотя, они не противоречат РКПМ). Измерения
в Гран Сассо, по-видимому, закрывают предсказания модели Волковой
и др. [21].
|
|
|
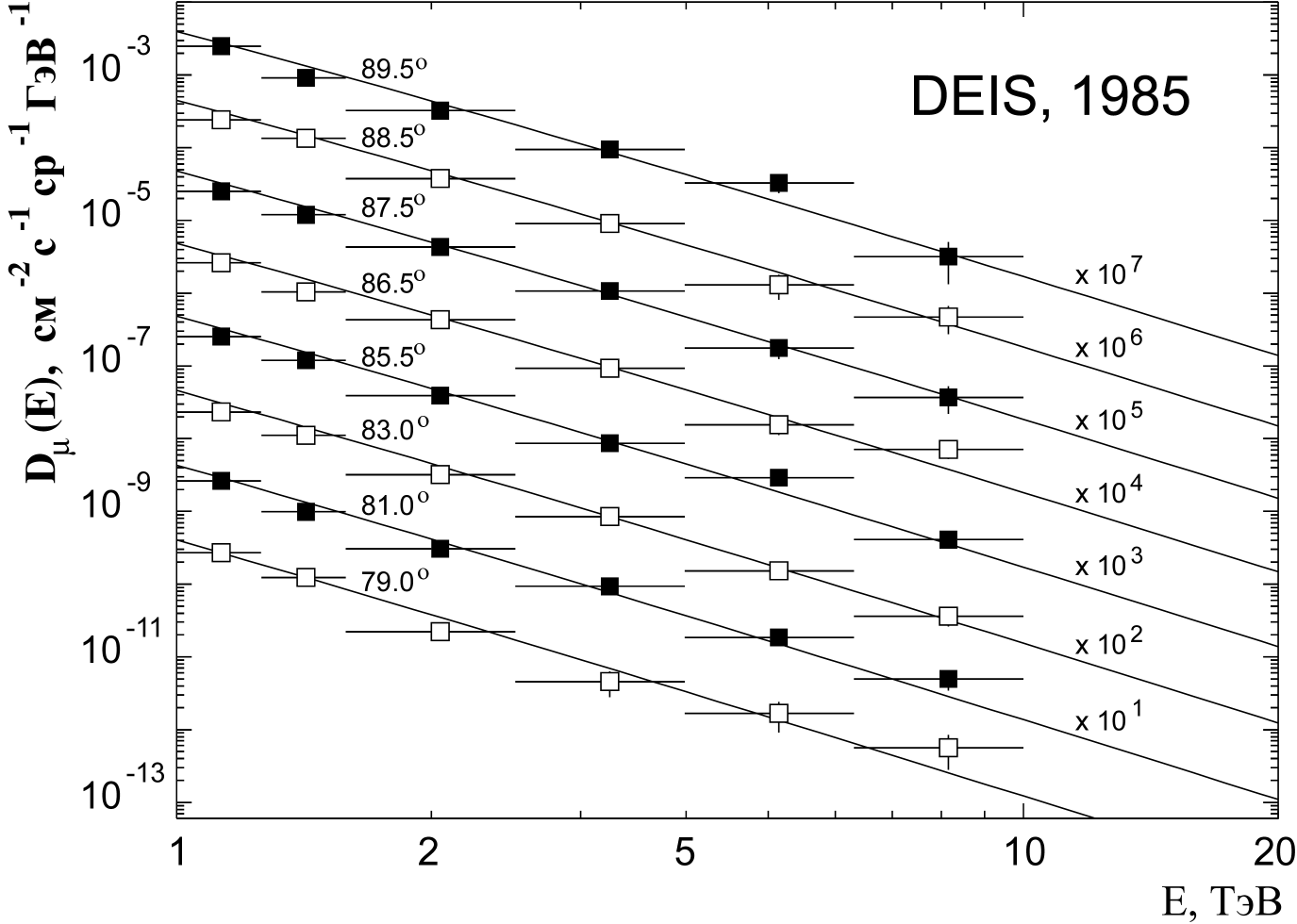
Рис. 3. Сравнение рассчитанных потоков мюонов на уровне моря с данными измерений спектрометра DEIS [11] в интервале зенитных углов 78.15°
- 90°
. |
Сравнение
с экспериментальными данными для зенитных углов 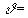 45°
, 72°
и 89° (рис. 2), а также с
измерениями спектрометра DEIS в интервале зенитных углов 78.15°
-90°
(рис.3), показывает хорошее согласие с рассчитанными энергетическими
спектрами (
45°
, 72°
и 89° (рис. 2), а также с
измерениями спектрометра DEIS в интервале зенитных углов 78.15°
-90°
(рис.3), показывает хорошее согласие с рассчитанными энергетическими
спектрами (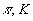 )
-мюонов.
)
-мюонов.
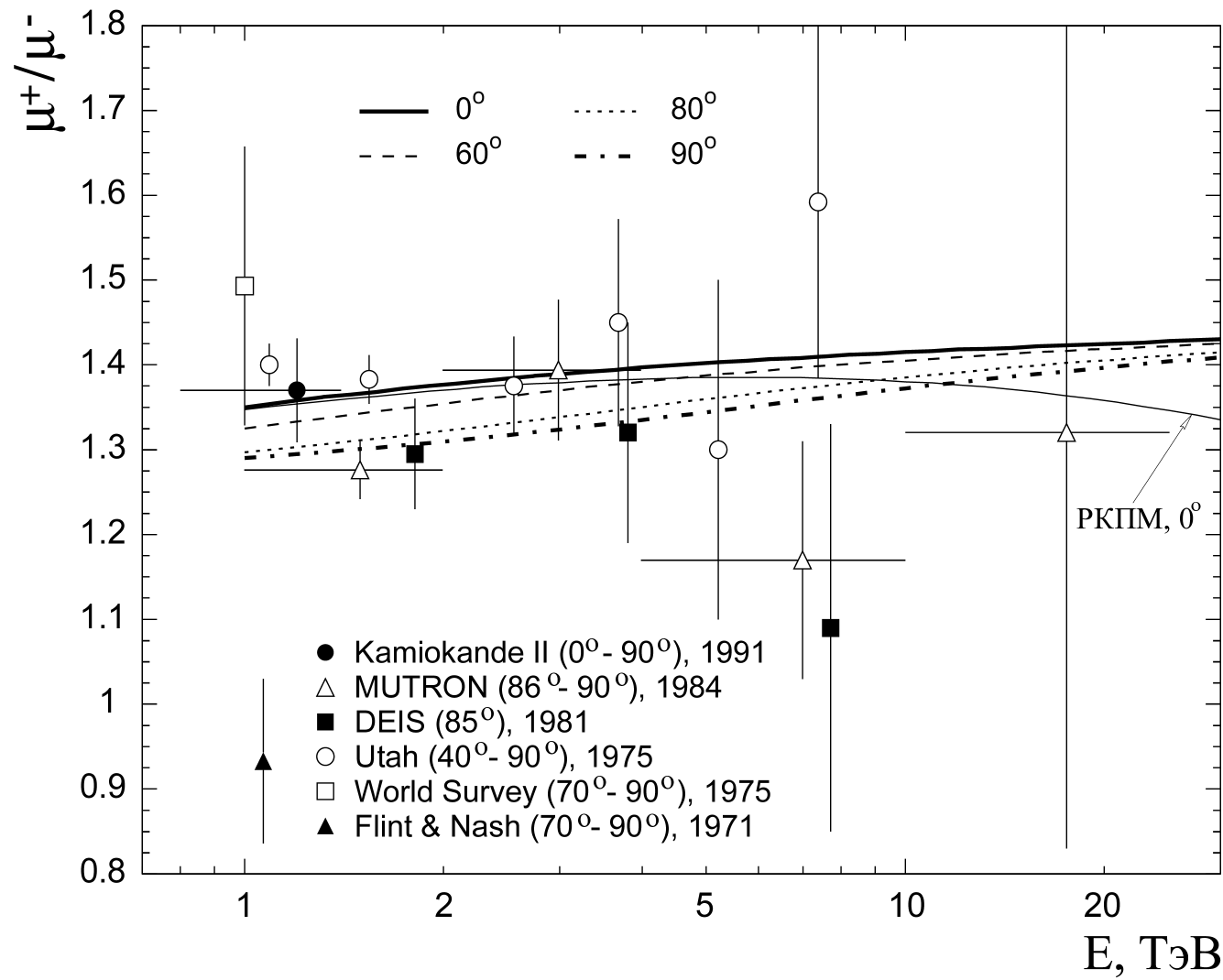
Результаты
расчета положительного избытка мюонов на уровне моря в зависимости
от энергии приведены на рис. 4. Сплошной (толстой), штриховой,
штрих-пунктирной и пунктирной линиями на рисунке изображено
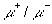 -отношение
для (
-отношение
для (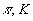 )-мюонов
при различных зенитных углах (
)-мюонов
при различных зенитных углах (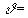 0°
, 60° , 80°
и 90°
соответственно). Тонкой сплошной линией показан расчет с учетом
вклада прямых мюонов на вертикали в рамках РКПМ. Вклад МКГС
мало влияет на зарядовое отношение.
0°
, 60° , 80°
и 90°
соответственно). Тонкой сплошной линией показан расчет с учетом
вклада прямых мюонов на вертикали в рамках РКПМ. Вклад МКГС
мало влияет на зарядовое отношение.
На рис.
4 также представлено сравнение рассчитанного 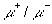 -отношения
с результатами измерений спектрометров MUTRON
(86° -90°
) [10], DEIS (85° )
[23], детектора Kamiokande II (0°
-90° )
[24], данными группы Utah (40°
-90° )
[25], данными для
-отношения
с результатами измерений спектрометров MUTRON
(86° -90°
) [10], DEIS (85° )
[23], детектора Kamiokande II (0°
-90° )
[24], данными группы Utah (40°
-90° )
[25], данными для 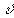 >70°
из обзора, приведенного
в работе [10] и c результатом более ранних экспериментов.
Последний (тёмный треугольник на рис. 4) получен в работе
[26] из обработки измерений пяти экспериментов. Все эти эксперименты
дают
>70°
из обзора, приведенного
в работе [10] и c результатом более ранних экспериментов.
Последний (тёмный треугольник на рис. 4) получен в работе
[26] из обработки измерений пяти экспериментов. Все эти эксперименты
дают 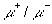 d
1 (см. ссылки в
[26]):
d
1 (см. ссылки в
[26]):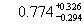 для
для 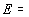 1090
ГэВ (MacKeown, 1965),
1090
ГэВ (MacKeown, 1965),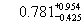 (Palmer и Nash,
1968), 0.9± 0.25 для
(Palmer и Nash,
1968), 0.9± 0.25 для 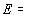 1080
ГэВ (Fujii, 1969),
1080
ГэВ (Fujii, 1969), 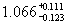 для
для 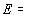 1095
ГэВ (Kamiya, 1969), 0.75±
0.4 для энергий от 1000 ГэВ до 1300 ГэВ (Alkofer, 1970), что
резко противоречит новым данным при
1095
ГэВ (Kamiya, 1969), 0.75±
0.4 для энергий от 1000 ГэВ до 1300 ГэВ (Alkofer, 1970), что
резко противоречит новым данным при 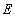 ~1
ТэВ.
~1
ТэВ.
|
|
|
Рис.
4 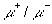 -отношение
на уровне моря для ( -отношение
на уровне моря для (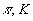 )-мюонов
при различных зенитных углах. Эксперимент: ▄
-[23], ∆, □ -[10] , â
-[24], ○ -[25], ▲ -[26]. )-мюонов
при различных зенитных углах. Эксперимент: ▄
-[23], ∆, □ -[10] , â
-[24], ○ -[25], ▲ -[26].
|
Поведение
зарядового отношения 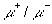 зависит от химического состава первичного излучения и от дифференциальных
сечений рождения пионов и каонов. Из сравнения рассчитанного
зависит от химического состава первичного излучения и от дифференциальных
сечений рождения пионов и каонов. Из сравнения рассчитанного
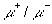 -отношения
с экспериментальными данными в принципе можно получить информацию
о деталях адронного каскада в атмосфере. Однако статистические
и систематические ошибки измерений зарядового отношения при
высоких энергиях настолько велики, что извлечь из них конкретную
информацию кажется проблематичным. Можно лишь утверждать,
что в целом рассчитанное
-отношения
с экспериментальными данными в принципе можно получить информацию
о деталях адронного каскада в атмосфере. Однако статистические
и систематические ошибки измерений зарядового отношения при
высоких энергиях настолько велики, что извлечь из них конкретную
информацию кажется проблематичным. Можно лишь утверждать,
что в целом рассчитанное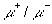 -отношение
не противоречит имеющимся данным.
-отношение
не противоречит имеющимся данным.
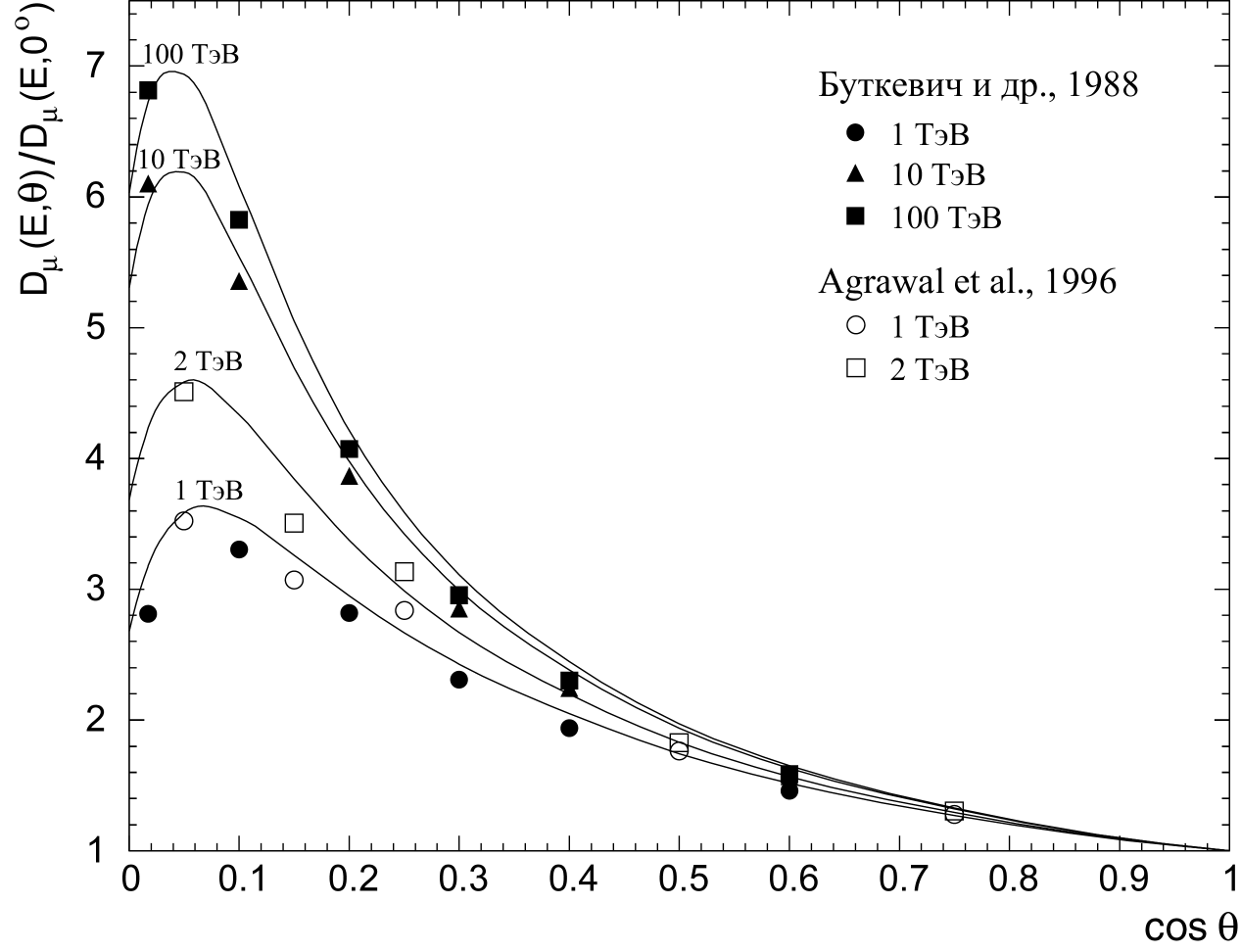
На рис.5
показано отношение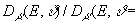 0°
), характеризующее
угловое усиление потоков мюонов, обусловленное относительным
увеличением вероятности
0°
), характеризующее
угловое усиление потоков мюонов, обусловленное относительным
увеличением вероятности 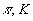 -распадов
c ростом зенитного угла. Имеется хорошее согласие с расчетом
[27] при
-распадов
c ростом зенитного угла. Имеется хорошее согласие с расчетом
[27] при 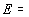 1
TэВ и 2 TэВ и видно некоторое расхождение с расчетом [28]
в области углов
1
TэВ и 2 TэВ и видно некоторое расхождение с расчетом [28]
в области углов 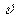 »
60° -80°
. Видимое различие
при
»
60° -80°
. Видимое различие
при 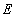 Í
1 ТэВ можно частично
отнести за счет выбора модели первичного спектра: в работе
[28] использовался спектр Раяна [29].
Í
1 ТэВ можно частично
отнести за счет выбора модели первичного спектра: в работе
[28] использовался спектр Раяна [29].
|
|
|
Рис.
5. Зенитно-угловые распределения (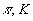 )-
мюонов на уровне моря для )-
мюонов на уровне моря для 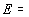 1,
2, 10 и 100
ТэВ. Кривые - данный расчет; точки:
○, □
- расчет [27]; ·
, ■, ▲
- расчет [28]. 1,
2, 10 и 100
ТэВ. Кривые - данный расчет; точки:
○, □
- расчет [27]; ·
, ■, ▲
- расчет [28].
|
Полученные энергетические спектры мюонов и угловые распределения исполь-зовались в качестве граничных спектров в задаче о прохождении мюонов через слой воды. Анализ энергетических спектров и угловых распределений глубоководных мюонов с учетом вклада распада чарма, рассчитанного для разных моделей рождения очарованных адронов, дан в работе [2].
4. Заключение
На основе
модели адронного каскада [3] были выполнены расчеты дифферен-циальных
энергетических спектров атмосферных мюонов для различных направлений.
В качестве дополнительных источников мюонов рассматривались
распады 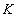 -мезонов
(
-мезонов
(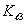 распады) и пионов, рожденных в распадах каонов. Учет этих
вкладов приводит к увеличению полных потоков мюонов на~5%.
Хотя эта поправка мала, она необходима для расчета спектров
мюонных и (особенно) электронных нейтрино, которые генерируются
в тех же процессах, что и мюоны.
распады) и пионов, рожденных в распадах каонов. Учет этих
вкладов приводит к увеличению полных потоков мюонов на~5%.
Хотя эта поправка мала, она необходима для расчета спектров
мюонных и (особенно) электронных нейтрино, которые генерируются
в тех же процессах, что и мюоны.
Данные
наземных и подземных измерений потоков мюонов противоречивы,хотя
большинство экспериментов имеют хорошую статистическую обеспеченность.
Это свидетельствует о наличии неучтенных систематических эффектов
в некоторых экспериментах. Ниже 5-6 ТэВ для вертикали наш
расчет потоков (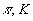 )-мюонов
находится в неплохом согласии как с прямыми, так и косвенными
измерениями. В области энергий выше 20 ТэВ существует некое
противоречие между данными Баксана, Frejus, МГУ и измерениями
LVD. Для данных LVD характерна высокая степень согласованности
пересчитанного к уровню моря спектра и кривой поглощения мюонов,
измеренной непосредственно на подземной установке, с нашим
расчетом. Для зенитных углов
)-мюонов
находится в неплохом согласии как с прямыми, так и косвенными
измерениями. В области энергий выше 20 ТэВ существует некое
противоречие между данными Баксана, Frejus, МГУ и измерениями
LVD. Для данных LVD характерна высокая степень согласованности
пересчитанного к уровню моря спектра и кривой поглощения мюонов,
измеренной непосредственно на подземной установке, с нашим
расчетом. Для зенитных углов 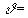 45°
, 72°
и 89° вычисленные дифференциальные
спектры близки к экспериментальным данным установок MUTRON,
DEIS, РЭК МГУ.
45°
, 72°
и 89° вычисленные дифференциальные
спектры близки к экспериментальным данным установок MUTRON,
DEIS, РЭК МГУ.
Таким образом, рассчитанные потоки и зарядовое отношение атмосферных мюонов для различных направлений на уровне моря описывают основную совокупность экспериментальных данных и согласуются расчетами других авторов [27, 28]. Это позволяет сделать вывод, что используемые в расчете модели адронного каскада и первичного спектра не противоречат эксперименту.
Автор благодарит В. А. Наумова за постановку задачи и руководство работой. Работа выполнена при финансовой поддержке Министерства образования РФ в рамках программы "Университеты России - фундаментальные исследования", грант № 728.
Литература
- Bugaev E.V., Misaki A., Naumov V.A. et al.//Phys. Rev. 1998 V D58 P. 054001.
- Misaki A., Naumov V.A., Sinegovskaya T. S. et al. Proc. of the 26th ICRC, Salt Lake City, Utah. 1999. V. 2. P. 139; hep-ph/9905399.
- Валл А.Н., Наумов В.А., Синеговский С.И. // ЯФ. 1986. Т. 44. С. 1240.
- Никольский С.И., Стаменов Й. И., Ушев С. З. // ЖЭТФ. 1984. Т. 87. С. 18.
- Наумов В.А., Синеговская Т.С., Синеговский C.И. В сб.: "Астрофизика и физика микромира. Материалы Байкальской школы по фундаментальной физике (11-17 октября 1998 г.Иркутск)''. Иркутск: изд-во ИГУ, 1998. С. 211.
- Naumov V.A, Sinegovskaya T.S, Sinegovsky S.I.//Nuovo Cim.1998 v111a, p129
- Nandi B.C. and Sinha M.S. // J. Phys. A: Gen. Phys. 1972. V. 5. P. 1384
- Rastin B.C. // J. Phys. G: Nucl. Phys. 1984. V. 10. P. 1609
- Thompson M.G. et al. // Proc. of the 15th ICRC, Plovdiv. 1977. V. 6. P. 21.
- Matsuno S. et al. // Phys. Rev. 1984. V. D29. P. 1.
- Allkofer O.C. et al. // Nucl. Phys. 1985. V. B259. P. 1.
- Kellog R.G., Kasha H., Larsen R.C. // Phys. Rev. 1978. V. D17. P. 98.
- Gettert M. et al. Proc. of the 23rd ICRC, Calgary, 1993. V. 4. P. 394.
- Khalchukov F.F. et al. Proc. of the 19th ICRC, La Jolla, California. 1985 v8. p12
- Зацепин Г.Т. и др. // Изв. РАН. Сер. Физ. 1994. Т. 58. С. 119.
- Ivanova M.A. et al. Proc. of the 16th ICRC, Kyoto. 1979. V. 10. P. 35.
- Бакатанов В.Н. и др. // ЯФ. 1992. Т. 55. С. 2107.
- Rhode W. // Nucl. Phys. (Proc. Suppl.). 1994. V. B35. P. 250
- Ambrosio M. et al. // Phys. Rev. 1995. V. D52. P. 3793.
- Aglietta M. et al. // Phys. Rev. 1998. V. D58. P. 092005.
- Volkova L.V. et al. // Nuovo Cim. 1987. V. 10C. P. 465.
- Pasquali L., Reno M.H. and Sarcevic I. // Phys. Rev. 1999. V. D59, P. 034020
- Allkofer O.C. et.al. Proc. of the 17th ICRC, Paris. 1981. V. 10. P. 321.
- Yamada M. et al. // Phys. Rev. 1991. V. D44. P. 617.
- Ashley G.K., Keuffel J.W., Larsona M.O. // Phys. Rev. 1975. V. D 12. P. 20.
- Flint R.W., Nash W.F. // Nucl. Phys. 1971. V. B33. P. 632.
- Agrawal V. et al. // Phys. Rev. 1996. V. D53. P. 1314.
- Буткевич А.В., Деденко Л.Г., Железных И.М. // ЯФ. 1988. Т. 50. С. 142.
Ryan M.J. et al. // Phys. Rev. Lett. 1972. V. 28. P. 985.

