ПЕРИОД ЦИКЛА И СВОЙСТВА СИММЕТРИИ ГЛОБАЛЬНОГО ПОЛЯ В МОДЕЛИ ДИНАМО

В. М. Мазур

Институт солнечно-земной физики СО РАН, Иркутск

Проблема периода и новые граничные условия. Первые модели динамо появились 30 лет назад. Уже они натолкнулись на существенную трудность – невозможность воспроизвести наблюдаемое значение периода солнечного цикла 22 года. Последующие модели если и смогли исправить это положение, то только в ущерб существующим представлениям о строении солнечной конвективной зоны. Еще одно расхождение моделей с наблюдениями связано с динамо-числом 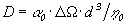. 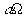Этот ключевой параметр моделей -динамо характеризует интенсивность перераспределения энергии между тороидальной и полоидальной компонентами поля, здесь 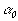и 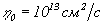- характерные значения для альфа-эффекта и турбулентной диффузии, 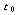- неоднородность угловой скорости в пределах системы (конвективной зоны), 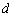- масштаб этой системы. Генерация полей становится возможной, если динамо-число превышает некоторое критическое значение .

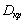Модели динамо, разработанные, например, Краузе и Рэдлером [1], в сферическом слое дают 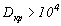. В этом случае 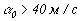и для отношения амплитуд полоидального и тороидального полей мы получаем оценку: 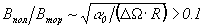, в то время как из наблюдений известно, что 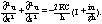. Таким образом, модели дают завышенное критическое динамо-число. Чем больше динамо-число, тем быстрее перераспределяется энергия между тороидальным и полоидальным полями, и, значит, тем меньше период цикла, и мы опять возвращаемся к проблеме периода. В чем же причина столь малых его расчетных значений?

Период любого циклического процесса, рождающегося в конкуренции механизмов генерации и диссипации, не может существенно превышать характерного времени затухания в системе. Если диффузия в конвективной зоне в целом изотропная, то указанное время определяется вертикальным масштабом – толщиной конвективной зоны 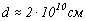: 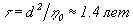. Положение исправляется если предположить, что по какой-то причине эффективность диффузии в вертикальном направлении ограничена. Горизонтальный масштаб имеет порядок солнечного радиуса и .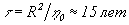

Обычные модели солнечного динамо используют т.н. вакуумные граничные условия для внешней поверхности конвективной оболочки: решение внутри последней сшивается с потенциальным решением для внешнего пространства. Такой подход предполагает возможность свободного выхода полей из конвективной зоны. Но, как указал Паркер [2], для этого полю необходимо освободиться от солнечного вещества, в которое оно вморожено. Более реалистичными, по его мнению, были бы сверхпроводниковые граничные условия, которые препятствуют проникновению поля через поверхность раздела. По оценке Паркера, не более 3% генерируемого в конвективной оболочке Солнца магнитного потока покидает ее.

Выход полей может быть связан с паркеровской неустойчивостью трубок тороидального поля по отношению к образованию петель вследствие плавучести [3]. В этом случае нормальная (вертикальная) составляющая вектора плотности потока энергии: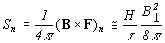

где 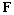- электродвижущая сила,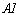- характерный масштаб неустойчивости, который можно принять равным шкале высот, 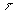- время развития неустойчивости, определяемое выражением 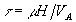, где 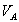- альфвеновская скорость, а 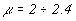- постоянная. Такое же выражение для 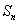получится, если связать горизонтальную компоненту ЭДС и магнитное поле соотношением:

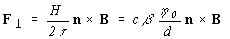
где 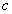- константа, большая единицы, 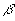- нормированная характерным значением напряженность поля.

Введя обозначение 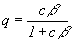, мы можем записать новые граничные условия для внешней поверхности конвективной зоны в виде: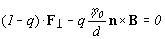

Легко видеть, что при 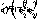получаются сверхпроводниковые условия (отсутствие горизонтальной ЭДС), а при 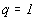т.н. псевдовакуумные условия, требующие исчезновения горизонтальной составляющей поля на границе раздела и хорошо воспроизводящие решения, получаемые с обычными вакуумными условиями. Таким образом, новые граничные условия представляют собой смесь двух крайних в смысле возможности выхода полей условий, а параметр 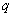регулирует примесь каждого из этих двух вариантов. Отметим так же, что конвективная зона излучает энергию (а не поглощает ее), если .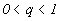

Модель динамо. При построении моделей динамо широко распространена практика включения в них большого числа свободных параметров, надлежащий подбор которых может воспроизвести любой наперед заданный результат. Мы, по возможности, пытались избегать такого произвола, используя либо данные, полученные из наблюдений, либо хорошо проработанные модели строения конвективной зоны. Последняя в нашей модели представляет собой сферический слой с толщиной 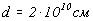и с внешним радиусом 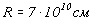. Электропроводящая жидкость, заполняющая объем слоя вращается дифференциально, закон вращения взят в форме, предложенной Кузаняном [4] и построенной по данным SOHO. Эволюция магнитного поля в этой системе описывается уравнением индукции, включающим 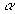-эффект, турбулентную диффузию с учетом анизотропии, а так же конвективный перенос поля, возникающий вследствие неоднородности плотности среды. Профили термодинамических параметров заимствованы из модели Штикса строения конвективной оболочки Солнца. Учтено подавление турбулентных коэффициентов вращением. Итак, динамика магнитного поля описывается уравнением:

, ,

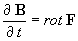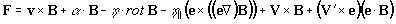где - скорость, 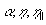- профили 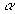-эффекта и двух компонент тензора турбулентной диффузии (изотропной и отвечающей за направление, выделенное вращением: 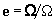), 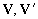- эффективные скорости турбулентного переноса поля.

Для нижней поверхности слоя использовались сверхпроводниковые гранусловия, для верхней – новые, причем для обеспечения линейности задачи параметр 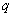, вообще говоря, зависящий от напряженности поля, не фиксировался. Нашей задачей было определение зависимостей порогового значения 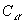(см. ниже) и периода поля от этого параметра. Тем самым, помимо прочего, определяется и область амплитуд поля, для которых следует проводить нелинейное исследование.

Линейное исследование проводилось в рамках 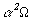-динамо с ключевыми параметрам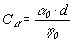и и .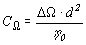

Второй является фиксированным, а первый может свободно меняться, регулируя скорость накачки, так что его можно использовать вместо динамо-числа, являющегося произведением этих двух параметров.

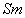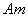Мы рассматривали моды магнитного поля с различным характером симметрии относительно оси вращения и относительно экваториальной плоскости. Такие моды получили обозначения или , где 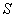соответствует симметричным относительно экватора модам, 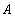– антисимметричным, 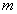– азимутальное волновое число (мы ограничились рассмотрением случаев 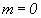и ).

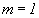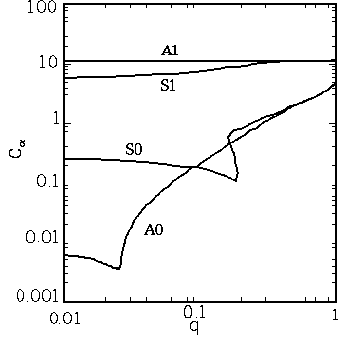
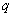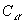Результаты и обсуждение. На рис. 1 показана диаграмма устойчивости четырех мод глобального поля в координатах двух свободных параметров нашей модели и . Как можно видеть, осесимметричные моды преобладают над неосесимметричными во всем диапазоне значений 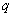. В связи с этим следует отметить, что дифференциальное вращение вообще не благоволит неосесимметричным модам, вынуждая их либо убегать в области, где дифференциальность вращения мала, либо приобретать тонкую структуру в направлении наибольшей неоднородности и бороться с сильной диффузией. Этот результат получил еще Рэдлер, и он с успехом подтверждается в нашей модели: мода 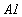сжимается к экватору, где неоднородность вращения меньше, а мода 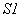имеет тонкую структуру по широте. Ясно, что уменьшение масштаба моды требует больших затрат энергии на ее поддержание, т.е. больших 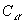. Объяснение наблюдаемым проявлениям неосесимметричности глобального поля Солнца следует, по-видимому, искать так или иначе за пределами конвективной зоны, например, в присутствии реликтового поля, выступающего в отношении последней как внешний возбуждающий источник.

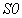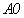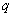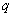Обратимся теперь к осесимметричным полям. Как видно из рис. 1, кривые и идут близко друг к другу, иногда пересекаясь. Забегая вперед, скажем, что, по-видимому, для интересующего нас значения , т.е. для того значения, которое воспроизводит наблюдаемую продолжительность солнечного цикла, преобладает все же антисимметричная мода, хотя для близких значений она уступает место симметричной. Это обстоятельство может пролить свет на проблему маундеровского минимума, которую связывают с повышением веса квадрупольной составляющей в глобальном магнитном поле Солнца: всегда имеющие место флуктуации могут выводить систему в область значений 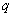, где преобладает квадруполь. Впрочем, конечно, этот вопрос требует отдельного тщательного изучения.

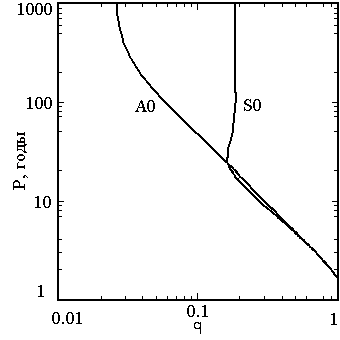
На рис.2 показана зависимость периодов двух осесимметричных мод от параметра 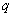. Как и ожидалось, период неограниченно растет с уменьшением 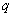, т.е. по мере “закрывания” верхней границы. Для псевдовакуумных условий (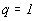) период 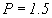года слишком мал. Наблюдаемое значение 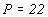года достигается при 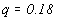. Отметим, что квадрупольная мода имеет здесь примерно такой же период. Асимптотики на второй и изломы кривых на первой диаграммах связаны с тем, что для достаточно малых 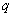существуют стационарные моды.

Рис. 1 Диаграмма устойчивости четырех мод магнитного поля в координатах свободных параметров задач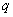и и 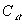. Преобладание осесимметричных мод	Рис. 2 Зависимости периодов 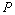двух осесимметричных мод магнитного поля от параметра 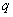граничных условий. Неограниченный рост периода по мере перехода к сверхпроводниковым условиям

К сожалению, включение турбулентных переносов не помогло решить давно стоящую проблему, связанную с характером миграции поясов тороидального поля. Последние, как и прежде, появляются и на высоких широтах, где им не следовало бы быть. Возможно, решение этой проблемы кроется все же в учете меридиональных течений. Дальнейшие успехи гелиосейсмологии, вероятно, прояснят этот вопрос.

Решение этой и других проблем, оставшихся от линейного исследования должно быть продолжено в рамках нелинейного подхода, включающего подавление турбулентных коэффициентов магнитным полем, а так же зависимость от последнего характера выхода полей из конвективной оболочки (параметра ).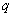

Литература

1. Краузе Ф., Рэдлер К.-Х. Магнитная гидродинамика средних полей и теория динамо. М: Мир, 1984.
2. Parker E.N. // Astrophys. J. 1984. V.281. P.839.
3. Паркер Е. // Космические магнитные поля. М: Мир, 1982.

Кузанян К.М., частное сообщение.