ВОССТАНОВЛЕНИЕ ПРОФИЛЯ ЭЛЕКТРОННОЙ КОНЦЕНТРАЦИИ ПО ДАННЫМ GPS: ПЕРВЫЕ РЕЗУЛЬТАТЫ
К. С. Паламарчук
Институт солнечно-земной физики СО РАН, Иркутск
1. Постановка проблемы
При трансионосферном зондировании сигналами искусственных спутников Земли (ИСЗ) в приближении сферически-симметричной ионосферы полное электронное содержание (ПЭС) вдоль луча зрения, составляющего с зенитом угол q
, как можно видеть из рисунка 1, составляет
|
|
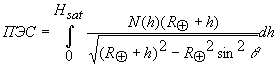
(1) |
где N(h) — электронная концентрация на высоте h, RЕ — радиус Земли, Hsat — высота полета ИСЗ [1].
ПЭС(q
) может быть измерено различными способами. Среди перспективных способов измерения этой зависимости выделяются измерения фазовых и групповых задержек сигналов радионавигационных систем GPS и ГЛОНАСС, которые позволяют достичь высокой точности и хорошего временного разрешения. Такие измерения производятся стандартизованным оборудованием сотнями станций по всему земному шару, из результаты доступны через Internet [3].
Уравнение (1) является интегральным уравнением Фредгольма первого рода по отношению к N(h). Решение этого уравнения могло бы дать информацию о профиле электронной концентрации. Однако задача решения уравнения типа (1) принадлежит к классу некорректных задач, то есть задач, решение которых катастрофически зависит от ошибок во входных данных, в нашем случае от ошибок измерения ПЭС(q
). Одним из широко применяемых методов получения приближенного, но устойчивого решения, является регуляризация, под которой понимается минимизация функционала
|
|
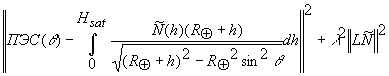
(2) |
где ПЭС — измеренная
величина,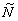 
— регуляризационное решение, L
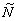—регуляризирующий
функционал (вводимый для “оценки качества решения”), l
— параметр регуляризации (смысл которого состоит в установлении
балланса между “качеством решения” и невязкой). В настоящей
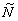работе рассматривался исключительно случай L=0,
что соответствует поиску решения, наиболее точно удовлетворяющего
уравнению (1). Выбор оптимальногй формы для регуляризационного
функционала сам по себе является отдельной сложной задачей.
Наиболее удобным методом для осуществления минимизации представляется
метод сопряженных градиентов (МСГ) [2].
Однако этот метод является итерационным, а потому весьма чувствителен
к выбору начального приближения. Начальное приближение может
быть выбрано исходя из подходящей модели ионосферы или независимого
измерения. Также в качестве начального приближения может быть
взят некий стандартный неизменный a-priori
профиль. Приемуществом
такого подхода является самодостаточность и отсутствие необходимости
во внешних ионосферных моделях или измерениях. Серьезнейшим
недостатком выступает чувствительность МСГ к выбору начального
приближения, из-за чего может ухудшиться скорость сходимости
итераций.
Четвертым способом выбора начального приближения может быть комбинация выбора a-priori профиля с последующей грубой его корректировкой посредством МСГ. При этом выполняется несколько последовательных серий итераций МСГ, причем результат каждой такой серии используется как начальное приближение для следующей серии. Последовательное уменьшение шага итераций от серии к серии позволяет сократить время, необходимое для получения очередного приближенного решения.
2. Численное моделирование
Для оценки эффективности такого подхода было проведено численное моделирование. Была выбрана параболическая модель ионосферы с высотой максимума 300 км, верхней и нижней границами 150 и 450 км, соответственно. Радиус Земли был принят равным 6400 км.
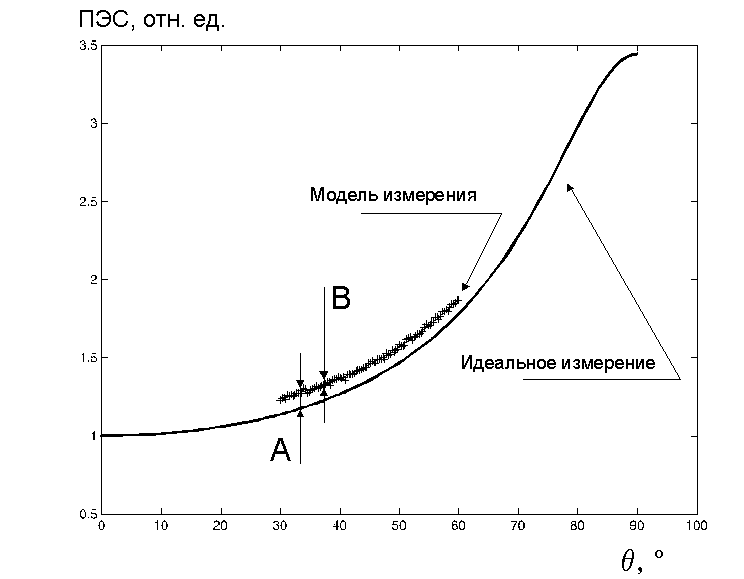
На первой стадии моделирования вычислялся “идеальный” ряд ПЭС(t) (рис. 2) Для последующих вычислений выбиралась лишь часть этого ряда, соответствующая типичным границам изменения q
30–40°
. Формирование “модели измерения” завершалось возмущением “идеального” ряда ПЭС прибавлением к нему некоторой постоянной константы А и случайного шума амплитуды B. А и B выбирались одного порядка с неопределенностью нуля и амплитуды шума измерений ПЭС, характерных для GPS.
|
|
|
Рис. 2. Ряды идеального измерения и модели реального измерения |
Вторая стадия моделирования состояла в применении описанного выше алгоритма последовательного уточнения решения с помощью МСГ.
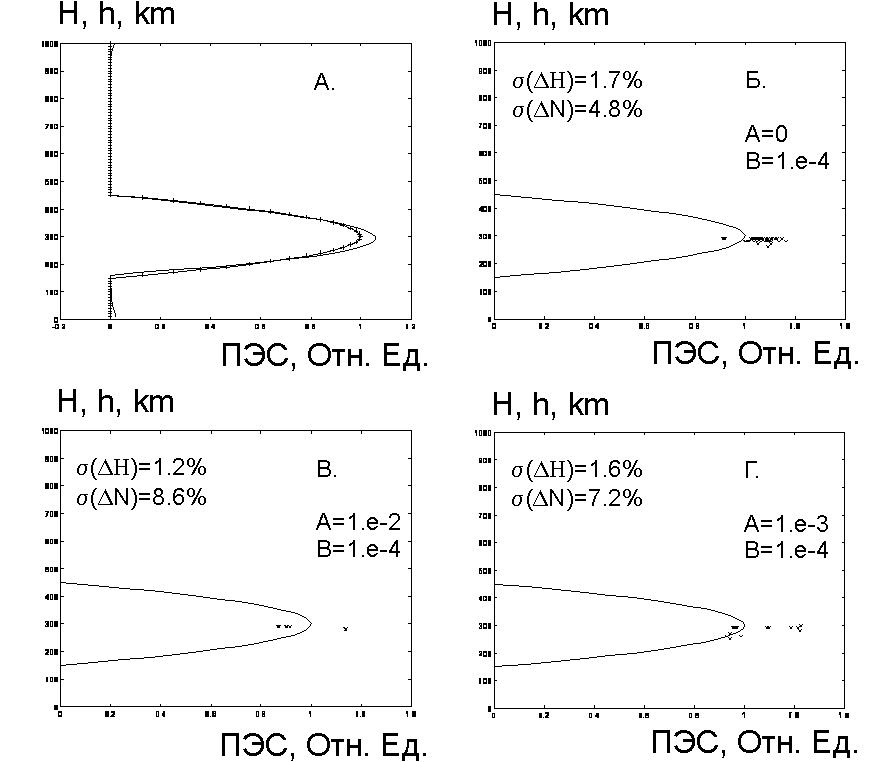
На рис. 3 представлены результаты восстановления модельного параболического ионосферного профиля. В качестве параметров для оценки успешности восстановления профиля были выбраны высота максимума и максимальная электронная концентрация. Можно видеть, что при параметрах шума, типичных для измерения ПЭС с помощью GPS и ГЛОНАСС, среднеквадратические отклонения высоты максимума электронной концентрации s
(D
H) не превосходят 1.7%, а максимальной концентрации электронов s
(D
N) – 8.6%.
Авторы статьи [1] оценивали только погрешность определения максимальной концентрации электронов, которая составляла 10%.
Таким образом, последовательное уточнение начального приближения с помощью МСГ может оказаться полезным при построении рабочих алгоритмов восстановления профиля электронной концентрации по данным трансионосферного зондирования.
|
|
|
Рис. 3. а. пример модельного (кресты) и восстановленного (линия) профилей
б, в, г. модельный профиль и положения максимумов восстановленного слоя (кресты) при различных параметрах шума А и B.
|
Литература
- Андрианов В. А., Смирнов В. М. Определение высотного профиля электронной концентрации ионосферы Земли по двухчастотным измерениям радиосигналов искусственных спутников Земли // Радиоэлектроника. — 1993. — Т. 38. — С. 1326–1335.
- Press W. H. et al. Numerical Recipes, The Art of Scientific Computing. Cambridge University Press, 1986.
Hofmann-Wellenhof B. Et al. Global Positioning System: Theory and Practice. Springer-Verlag, Wien, New-York, 1992.
