ТЕПЛОВАЯ СТРУКТУРА ПЛАЗМОСФЕРЫ ПРИ СИЛЬНОМ ГЕОМАГНИТНОМ ВОЗМУЩЕНИИ
И.А. Кринберг, М.А. Кручинина
Иркутский государственный университет
При быстром росте магнитосферного электрического поля увеличивается скорость электрического дрейфа, что приводит к неравномерному сжатию плазмы вдоль геомагнитных силовых трубок внешней плазмосферы. Показано, что при этом плазма ускоряется вдоль геомагнитного поля и нагревается. Нагрев происходит как следствие увеличения концентрации плазмы в магнитных силовых трубках за счет их поперечного сжатия.
Усиление магнитосферного
электрического поля Е в периоды сильных геомагнитных
возмущений приводит к увеличению скорости электрического дрейфа
U=cE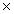 B/
B/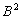 ,
которая направлена перпендикулярно магнитной силовой линии
и лежит в ее плоскости [1]. В ночном секторе плазмосферы,
где геомагнитное поле В можно считать дипольным,
в результате усиления такого дрейфа плазма быстро перемещается
из магнитных силовых трубок большого объема в трубки меньшего
объема. Сжатие плазмы оказывается неравномерным вдоль каждой
силовой трубки: более существенным на вершине трубки и минимальным
на ее концах, что связано с геометрией силовых линий геомагнитного
поля. Поэтому происходит неоднородное уплотнение и нагрев
плазмы - на вершине трубки плотность и температура растут
быстрее. Градиент давления, возникший в силовой трубке, заставляет
плазму ускоряться вдоль магнитного поля от вершины трубки
к концам. При этом к вершине трубки будет распространяться
волна разрежения, а к концам трубки будет идти волна сжатия.
В дальнейшем волна разрежения будет отражаться от вершины,
а волна сжатия - от концов трубки, в результате чего возникает
суперпозиция волн и развивается достаточно сложная волновая
картина. Данные явления исследовались нами ранее [2,3] на
примере одной плазменной трубки, конвектирующей с внешней
границы плазмосферы по направлению к Земле. В настоящей работе
рассматривается система трубок, что позволяет проследить эволюцию
параметров плазмы в пределах всей ночной плазмосферы в периоды
сильного геомагнитного возмущения, когда плазмосфера сжимается
[4] и, как будет показано ниже, существенно нагревается.
,
которая направлена перпендикулярно магнитной силовой линии
и лежит в ее плоскости [1]. В ночном секторе плазмосферы,
где геомагнитное поле В можно считать дипольным,
в результате усиления такого дрейфа плазма быстро перемещается
из магнитных силовых трубок большого объема в трубки меньшего
объема. Сжатие плазмы оказывается неравномерным вдоль каждой
силовой трубки: более существенным на вершине трубки и минимальным
на ее концах, что связано с геометрией силовых линий геомагнитного
поля. Поэтому происходит неоднородное уплотнение и нагрев
плазмы - на вершине трубки плотность и температура растут
быстрее. Градиент давления, возникший в силовой трубке, заставляет
плазму ускоряться вдоль магнитного поля от вершины трубки
к концам. При этом к вершине трубки будет распространяться
волна разрежения, а к концам трубки будет идти волна сжатия.
В дальнейшем волна разрежения будет отражаться от вершины,
а волна сжатия - от концов трубки, в результате чего возникает
суперпозиция волн и развивается достаточно сложная волновая
картина. Данные явления исследовались нами ранее [2,3] на
примере одной плазменной трубки, конвектирующей с внешней
границы плазмосферы по направлению к Земле. В настоящей работе
рассматривается система трубок, что позволяет проследить эволюцию
параметров плазмы в пределах всей ночной плазмосферы в периоды
сильного геомагнитного возмущения, когда плазмосфера сжимается
[4] и, как будет показано ниже, существенно нагревается.
Основные уравнения и численный метод
Для моделирования данных
эффектов численно решалась система нестационарных уравнений
одножидкостной гидродинамики, причем для расчета изменений
температуры использовалось адиабатическое приближение. Перемещение
плазмы в плазмосфере представлялось в виде суммы двух взаимно
перпендикулярных движений: течения плазмы вдоль геомагнитной
силовой трубки с продольной скоростью
V и
электрического дрейфа поперек силовых трубок со скоростью
U. Одномерное
течение газа (плазмы) с плотностью 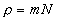 вдоль трубки с переменным сечением
вдоль трубки с переменным сечением 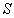 (L,x)
описывается системой [5,6]:
(L,x)
описывается системой [5,6]:
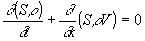 ,
(1)
,
(1)
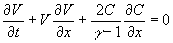 ,
(2)
,
(2)
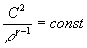 ,
(3)
,
(3)
Здесь 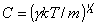 - скорость звука в среде,
- скорость звука в среде, 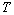 -
температура плазмы,
-
температура плазмы, 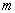 - масса протона,
- масса протона,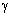 =5/3,
=5/3,
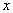 -
расстояние вдоль силовой линии, отсчитываемое от ее вершины.
Путем замены переменных
-
расстояние вдоль силовой линии, отсчитываемое от ее вершины.
Путем замены переменных 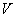 и
и  на инварианты Римана
на инварианты Римана 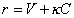 и
и 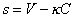 система уравнений 1,2,3 преобразуется в инвариантную форму
[5,6]:
система уравнений 1,2,3 преобразуется в инвариантную форму
[5,6]:
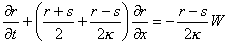 ,
(4)
,
(4)
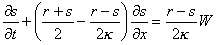 ,
(5)
,
(5)
где 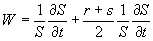 ,
,
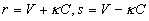 ,
,
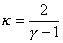 .
.
Электрический дрейф учитывался
в модели как изменение параметра 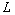 магнитной силовой трубки со временем, так как в результате
дрейфа плазма перемещается из одной трубки в другую трубку
с меньшим объемом. Так как электрический дрейф происходит
перпендикулярно магнитным силовым линиям, то плазма при этом
перемещается по линиям равного потенциала геомагнитного поля,
поэтому при переходе из одной трубки в другую расстояния между
узлами расчетной сетки изменялись, и их необходимо было пересчитывать.
Узлы расчетной сетки строились как пересечения магнитных силовых
линий с линиями равного потенциала. В предлагаемой модели
в начальный момент плазма была равномерно распределена вдоль
трубки
магнитной силовой трубки со временем, так как в результате
дрейфа плазма перемещается из одной трубки в другую трубку
с меньшим объемом. Так как электрический дрейф происходит
перпендикулярно магнитным силовым линиям, то плазма при этом
перемещается по линиям равного потенциала геомагнитного поля,
поэтому при переходе из одной трубки в другую расстояния между
узлами расчетной сетки изменялись, и их необходимо было пересчитывать.
Узлы расчетной сетки строились как пересечения магнитных силовых
линий с линиями равного потенциала. В предлагаемой модели
в начальный момент плазма была равномерно распределена вдоль
трубки 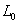 .
Решение системы уравнений:
.
Решение системы уравнений: 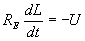 ,
U=cE
,
U=cE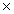 B/
B/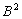 ,
где
,
где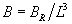 ,
,
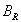 – значение магнитного поля на экваторе Земли,
– значение магнитного поля на экваторе Земли, 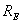 - радиус Земли, дает зависимость параметра
- радиус Земли, дает зависимость параметра 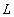 с течением времени:
с течением времени:
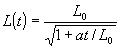 ,
(6)
,
(6)
где  ,
,
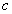 - скорость света.
- скорость света.
Таким образом, была
получена задача о квазиодномерном течении газа вдоль трубки,
размеры которой (сечение 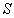 (L,x)
и длина) меняются со временем и на каждом временном шаге пересчитываются
координаты узлов расчетной сетки. Расчет параметров квазиодномерного
течения осуществлялся путем численного решения уравнений (4)
и (5) для инвариантов Римана, для этих уравнений использовалась
явная разностная схема.
(L,x)
и длина) меняются со временем и на каждом временном шаге пересчитываются
координаты узлов расчетной сетки. Расчет параметров квазиодномерного
течения осуществлялся путем численного решения уравнений (4)
и (5) для инвариантов Римана, для этих уравнений использовалась
явная разностная схема.
Граничные условия были следующими: относительно вершины трубки движение плазмы считалось симметричным, а на концах (на высоте около 1300 км над Землей) силовая трубка была “открытой”, плазма могла выходить через ее концы (область сужения).
Входные данные и результаты расчета
В предыдущих наших работах
[2,3] расчеты проводились только для одной магнитной силовой
трубки с 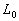 =6
[9]. Были исследованы распределения продольной скорости, плотности,
температуры и плотности потока плазмы вдоль силовой трубки.
В настоящей работе аналогичные расчеты были проведены для
20 трубок с начальным значением
=6
[9]. Были исследованы распределения продольной скорости, плотности,
температуры и плотности потока плазмы вдоль силовой трубки.
В настоящей работе аналогичные расчеты были проведены для
20 трубок с начальным значением 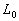 от 3 до 6. Было принято, что в начальный момент времени индекс
геомагнитной активности
от 3 до 6. Было принято, что в начальный момент времени индекс
геомагнитной активности 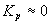 ,
что соответствует спокойным геомагнитным условиям, когда напряженность
магнитосферного электрического поля порядка
,
что соответствует спокойным геомагнитным условиям, когда напряженность
магнитосферного электрического поля порядка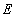 =0,07
В/км, а граница ночной плазмосферы находится на
=0,07
В/км, а граница ночной плазмосферы находится на 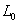 =6
[1]. В это время плазма считалась равномерно распределенной
вдоль каждой магнитной силовой трубки. Для трубки с
=6
[1]. В это время плазма считалась равномерно распределенной
вдоль каждой магнитной силовой трубки. Для трубки с 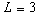 начальная концентрация принималась равной
начальная концентрация принималась равной 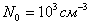 ,
а для других трубок она вычислялась по соотношению
,
а для других трубок она вычислялась по соотношению 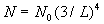 .
Считалось, что в начальный момент плазма во всех трубках неподвижна
(
.
Считалось, что в начальный момент плазма во всех трубках неподвижна
(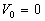 )
и имеет одинаковую температуру
)
и имеет одинаковую температуру 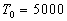 K.
Геомагнитное возмущение моделировалось путем задания скачкообразного
увеличения магнитосферного электрического поля до значения
Е=0,3 В/км, что соответствует
K.
Геомагнитное возмущение моделировалось путем задания скачкообразного
увеличения магнитосферного электрического поля до значения
Е=0,3 В/км, что соответствует 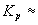 5
и согласуется с измерениями во внешней плазмосфере [7]. Во
все последующие моменты это значение электрического поля сохранялось.
5
и согласуется с измерениями во внешней плазмосфере [7]. Во
все последующие моменты это значение электрического поля сохранялось.
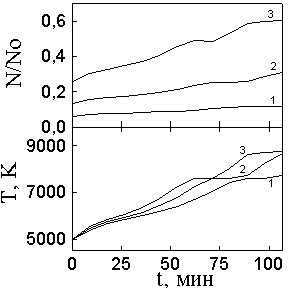
На рисунке 1 показана
временная зависимость концентрации и температуры плазмы на
вершине выделенной силовой трубки, которая в начальный момент
времени имеет значение: 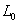 =6
( кривая 1),
=6
( кривая 1), 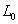 =5
(кривая 2),
=5
(кривая 2), 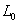 =4
(кривая 3). Сильное геомагнитное возмущение, выраженное в
усилении электрического дрейфа, приводит к сжатию плазмосферы.
Каждая магнитная силовая трубка уменьшается в размерах, в
результате чего концентрация в этих трубках и температура
со временем увеличиваются. Из рисунка 1 видно, что на вершине
силовых трубок концентрация через два часа от начала возмущения
увеличивается почти в два раза по сравнению с первоначальной.
Рост температуры объясняется сжатием каждой дрейфующей плазменной
трубки (параметры которой со временем меняются по закону (6))
и определяется соотношением
=4
(кривая 3). Сильное геомагнитное возмущение, выраженное в
усилении электрического дрейфа, приводит к сжатию плазмосферы.
Каждая магнитная силовая трубка уменьшается в размерах, в
результате чего концентрация в этих трубках и температура
со временем увеличиваются. Из рисунка 1 видно, что на вершине
силовых трубок концентрация через два часа от начала возмущения
увеличивается почти в два раза по сравнению с первоначальной.
Рост температуры объясняется сжатием каждой дрейфующей плазменной
трубки (параметры которой со временем меняются по закону (6))
и определяется соотношением 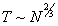 между
температурой и плотностью.
между
температурой и плотностью.
|
|
Рис.1. Временная
зависимость плотности и температуры на вершине выделенной
силовой трубки с начальным значением: 1-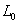 =6;
2- =6;
2-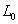 =5;
3- =5;
3-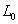 =4. =4.
|
На рисунке 2 показано
распределение плотности и температуры плазмы в плоскости геомагнитного
экватора поперек силовых линий в разные моменты времени от
начала геомагнитного возмущения. Этот рисунок удалось получить
благодаря тому, что были проведены расчеты одновременно для
20 различных силовых трубок с начальными значениями 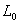 от 3 до 6. Первоначально плазмосфера была нагрета равномерно,
ее температура составляла 5000 К, а начальная плотность в
каждой силовой трубке зависела от номера L силовой трубки
от 3 до 6. Первоначально плазмосфера была нагрета равномерно,
ее температура составляла 5000 К, а начальная плотность в
каждой силовой трубке зависела от номера L силовой трубки
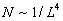 (кривая 1, рис.2). Со временем происходит опустошение больших
силовых трубок, картинка для плотности смешается в сторону
уменьшения L (рис.2). Если выбрать фиксированную силовую трубку,
например L=4, то в ней со временем, как видно из рисунка 2,
плотность плазмы уменьшается по сравнению с начальным значением,
через два часа после начала возмущения плотность плазмы в
этой трубке падает в два раза. Распределение температуры поперек
геомагнитного поля в ночном секторе плазмосферы выглядит иначе.
Через полчаса после начала геомагнитного возмущения температура
с 5000 К повышается до 6000 К, через полтора часа температура
достигает значений 7500-8000 К, а через два часа максимальное
значение температуры составляет 8700К.
(кривая 1, рис.2). Со временем происходит опустошение больших
силовых трубок, картинка для плотности смешается в сторону
уменьшения L (рис.2). Если выбрать фиксированную силовую трубку,
например L=4, то в ней со временем, как видно из рисунка 2,
плотность плазмы уменьшается по сравнению с начальным значением,
через два часа после начала возмущения плотность плазмы в
этой трубке падает в два раза. Распределение температуры поперек
геомагнитного поля в ночном секторе плазмосферы выглядит иначе.
Через полчаса после начала геомагнитного возмущения температура
с 5000 К повышается до 6000 К, через полтора часа температура
достигает значений 7500-8000 К, а через два часа максимальное
значение температуры составляет 8700К.
|
|
Рис.2. Распределение плотности и температуры в плоскости геомагнитного экватора (ночная плазмосфера) в различные моменты времени от начала геомагнитного возмущения (1 – t=0, 2-5 – t=27, 54, 81 и 108 минут).
L,R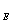
|
Для фиксированной магнитной
силовой трубки с L=4 температура за два часа увеличивается
от 5000К до 8000К, в то время как плотность для этой трубки
уменьшается в 2 раза. Эти результаты объясняются тем, что
адиабатическое приближение выполняется лишь для каждой выделенной
плазменной трубки, размеры которой меняются со временем по
закону (6). А если рассматривать фиксированную в пространстве
силовую трубку (например, L=4), то для нее адиабатическое
приближение не выполняется, поскольку через эту фиксированную
трубку со временем проходит множество различных плазменных
трубок, которые в начальный момент находились внутри силовых
трубок со значениями 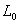 от 4 до 6. То есть для фиксированной трубки в уравнении
от 4 до 6. То есть для фиксированной трубки в уравнении  (адиабатическое приближение) константа в каждый момент времени
будет иметь разные значения. Таким образом, в ночном секторе
плазмосферы в результате геомагнитного возмущения в течении
двух часов после его начала наблюдается неизменный рост температуры
на фоне уменьшения плотности плазмы.
(адиабатическое приближение) константа в каждый момент времени
будет иметь разные значения. Таким образом, в ночном секторе
плазмосферы в результате геомагнитного возмущения в течении
двух часов после его начала наблюдается неизменный рост температуры
на фоне уменьшения плотности плазмы.
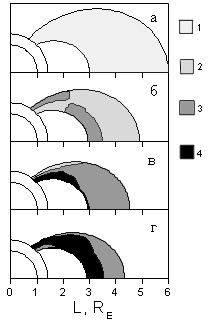
В работе также была исследована тепловая пространственная структура внешней плазмосферы. На рисунке 3 приведено изменение температуры плазмосферы во время геомагнитного возмущения спустя час от начала, полтора часа, два часа. Значения температуры показаны в диапазонах 6000-7000К, 7000-8000К, 8000-9000К.
|
|
Рис.3. Изменение температуры плазмосферы во время геомагнитного возмущения:
а, б, в, г – 0, 1 час, 1.5 часа, 2 часа от начала возмущения;
1, 2, 3, 4 - значения
электронной температуры 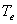 =5000K, =5000K,
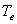 =6000-7000K, =6000-7000K,
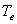 =7000-8000K, =7000-8000K,
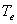 =8000-9000K. =8000-9000K.
|
Как уже говорилось, первоначальная
температура всей исследуемой области плазмосферы была 5000К
(рис.3.а). Спустя
полчаса от начала возмущения плазмосфера нагрелась до температур
6000-7500К. При этом максимальное значение 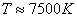 температура принимала в субавроральной области силовой трубки
с
температура принимала в субавроральной области силовой трубки
с 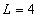 .
Через час плазмосфера была разделена на две области с разными
диапазонами температур: первая область с температурами от
6000-7000 К, вторая область – 7000-8000К, причем вторая область
занимает меньшие силовые трубки плазмосферы. Далее со временем
вторая область как бы вытесняет первую, то есть нагрев плазмы
начинается с малых трубок на их концах, а затем тепло передается
к вершинам этих трубок и переходит на все большие силовые
трубки. То есть процесс нагрева плазмосферы выглядит таким
образом, как будто источник тепла расположен на конце самой
меньшей силовой трубки. За полтора часа от начала возмущения
большая часть плазмосферы была нагрета до температур 7000-9000К.
И, наконец, спустя почти два часа от начала возмущения практически
вся плазмосфера оказывается нагретой до температур 8000-9500К.
Только небольшой участок плазмосферы на конце силовой трубки
с
.
Через час плазмосфера была разделена на две области с разными
диапазонами температур: первая область с температурами от
6000-7000 К, вторая область – 7000-8000К, причем вторая область
занимает меньшие силовые трубки плазмосферы. Далее со временем
вторая область как бы вытесняет первую, то есть нагрев плазмы
начинается с малых трубок на их концах, а затем тепло передается
к вершинам этих трубок и переходит на все большие силовые
трубки. То есть процесс нагрева плазмосферы выглядит таким
образом, как будто источник тепла расположен на конце самой
меньшей силовой трубки. За полтора часа от начала возмущения
большая часть плазмосферы была нагрета до температур 7000-9000К.
И, наконец, спустя почти два часа от начала возмущения практически
вся плазмосфера оказывается нагретой до температур 8000-9500К.
Только небольшой участок плазмосферы на конце силовой трубки
с 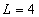 является относительно холодным с температурой от 7000 до 8000К,
что можно объяснить потерей “нагретых” частиц плазмы в результате
их вытекания из плазмосферы в субавроральную ионосферу.
является относительно холодным с температурой от 7000 до 8000К,
что можно объяснить потерей “нагретых” частиц плазмы в результате
их вытекания из плазмосферы в субавроральную ионосферу.
Основные выводы
Проведенные расчеты показали следующее.
- В результате усиления скорости электрического дрейфа во время геомагнитного возмущения в каждой дрейфующей плазменной трубке увеличивается плотность плазмы, что ведет к соответствующему росту температуры плазмы.
- В ночном секторе плазмосферы в плоскости геомагнитного экватора в результате геомагнитного возмущения в течении двух часов после его начала наблюдается неизменный рост температуры на фоне уменьшения плотности плазмы. Температура увеличивается от 5000К до 8000-8800К.
- Тепловая пространственная структура плазмосферы в результате геомагнитного возмущения претерпевает сильные изменения. За два часа от начала геомагнитного возмущения плазмосфера, имеющая первоначальную температуру 5000 К, нагревается до значений 8000-9500 К. В целом происходит нагрев всей исследуемой ночной области плазмосферы в 1,5-2 раза.
Литература
- Кринберг И.А., Тащилин А.В. Ионосфера и плазмосфера. “Наука”, М., 1984.
- Кринберг И.А., Кручинина М.А. Сб. Межд. конф. ”Физика ионосферы и атмосферы Земли” (тезисы докладов). Иркутск,1998.
- Кринберг И.А., Кручинина М.А. Сб. Исслед. По геомагн., аэрономии и физике Солнца. Иркутск.1999. Вып. ,
- Park C.G. J. Geophys. Res. 1973. V.78. N4. 672-683.
- Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М., 1978.
- Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М., 1975.
Carpenter D.L., Park C.G., Miller T.R.//J.Geophys.Res.1979.V.84A.N11.6559-6563.

