АНАЛИЗ СПЕКТРОВ СИГНАЛОВ ОДНОКРАТНОГО РАССЕЯНИЯ ОТ СЛУЧАЙНО-НЕОДНОРОДНЫХ СРЕД
О. И. Бернгардт, А.П. Потехин
Институт cолнечно-земной физики СО РАН, Иркутск
В работе на основе оригинального метода получено радиолокационное уравнение связывающее спектр сигнала однократного рассеяния с пространственно-временным спектром флуктуаций диэлектрической проницаемости среды. Уравнение получено без введения предположений о малости зондирующего объема или малости радиуса пространственной корреляции. На основе полученного радиолокационного уравнения предложена модель рассеяния на пространственных гармониках флуктуаций диэлектрической проницаемости. На примере анализа экспериментальных данных Иркутского радара некогерентного рассеяния(НР) и радара НР Милстон-Хилла показана эффективность модели для объяснения спектров рассеянного сигнала без дополнительных усреднений.
Введение
При радиолокационном зондирования атмосферы и ионосферы широко используется метод обратного рассеяния волн на мелкомасштабных флуктуациях среды. В этом случае не выполняется условие малости рассеивающего объема (которое обычно выполняется в лабораторных экспериментах [1-3]), поскольку его размеры определяются диаграммами направленности приемной и передающей антенн и растут с увеличением радиолокационной дальности. При этом, в области рассеяния нельзя заменить для падающей и рассеянной волн сферические фронты на плоские и стандартным образом установить достаточно простую связь сигнала с пространственным спектром флуктуаций[2-3]. Поэтому обычно анализируют статистические характеристики рассеянного сигнала (среднюю спектральную мощность, например).
Наиболее перспективной методикой при зондировании методом некогерентного рассеяния является регистрация полной формы рассеянного сигнала с ее последующей обработкой. Однако, существующие до сих пор методики обработки полной формы рассеянного сигнала либо не отличаются от статистической постановки задачи - измерения средних характеристик рассеянного сигнала, либо не выходят за рамки стандартной радиолокационной задачи - определения местоположения и скорости движения точечной цели. Теория последнего метода достаточно хорошо изучена и соответствует рассеянию на малых частицах[1-3]. Радиолокационные методы применяются, в частности, при интерпретации сигналов, рассеянных на метеорах и метеорных следах[4]. Однако, распространение данных методик на “распределенную” цель, которой является ионосфера, по видимому, не совсем правомочно вследствие больших размеров рассеивающей среды.
Для построения методик обработки полной формы сигнала необходимо построение радиолокационного уравнения, связывающего спектр рассеянного сигнала с пространственно-временным спектром флуктуаций диэлектрической проницаемости среды в реальной постановке эксперимента по зондированию среды.
В работе предложена методика построения такого радиолокационного уравнения и показана возможность его применения для интерпретации спектров рассеянного сигнала без дополнительного усреднения на примере данных двух радаров НР.
1.Радиолокационное уравнение для произвольных радиусов пространственной корреляции
При анализе рассеянного сигнала будем исходить из борновского приближения однократного рассеяния[1], дающего следующее выражение для огибающей рассеянного сигнала (без учета несущественных для последующего анализа множителей):
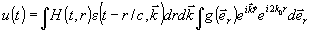 (1)
(1)
где 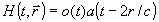 (2)
(2)
 - соответственно временное окно приема и комплексная огибающая излучаемого сигнала;
окно и сигнал узкополосны и имеют полосы
- соответственно временное окно приема и комплексная огибающая излучаемого сигнала;
окно и сигнал узкополосны и имеют полосы  ;
;
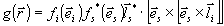 - диаграммный множитель, где
- диаграммный множитель, где 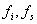 - диаграммы антенны на передачу и прием,
- диаграммы антенны на передачу и прием, 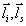 - их поляризационные множители,
- их поляризационные множители, 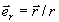 .
Выражение (1) получено в предположении, что рассеивающий объем находится в дальней
зоне антенны
.
Выражение (1) получено в предположении, что рассеивающий объем находится в дальней
зоне антенны 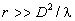 ,
где D - характерные размеры антенны,
,
где D - характерные размеры антенны, 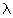 -
длина волны излучаемого сигнала.
-
длина волны излучаемого сигнала.
Выделим в (1) интеграл по единичной сфере и исследуем его:
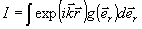 (3)
(3)
Подынтегральное выражение содержит быстро осциллирующую функцию, удовлетворяющую требованиям метода стационарной фазы (МСФ)[5]. Условие стационарности фазы записывается в виде
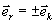 . (4)
. (4)
Тогда в первом приближении интеграл (3) равен сумме вкладов от стационарных точек:
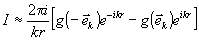 . (5)
. (5)
Таким образом, основной вклад в интеграл (3) дают "синфазные" области пространственных
гармонических решеток, оси которых направлены вдоль волнового вектора, а угловая
ширина определяется второй производной фазы в стационарной точке и равна 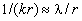 (что соответствует пространственному размеру
(что соответствует пространственному размеру 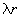 - квадрату радиуса Френеля). Это означает, что при рассеянии на решетке основной
вклад в рассеяние дает область, размеры которой по порядку величины равны радиусу
Френеля. Основным в (5) является первый член, поскольку второй имеет положительную
фазу и практически не дает вклада в (1) при интегрировании.
- квадрату радиуса Френеля). Это означает, что при рассеянии на решетке основной
вклад в рассеяние дает область, размеры которой по порядку величины равны радиусу
Френеля. Основным в (5) является первый член, поскольку второй имеет положительную
фазу и практически не дает вклада в (1) при интегрировании.
Подставляя (5) в (1), получаем выражение, связывающее спектр принятого сигнала со спектром неоднородностей среды:
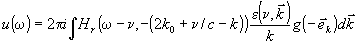 . (6)
. (6)
Здесь введено эффективное ядро
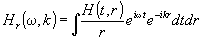 (7)
(7)
Как видно из полученной формулы, при однопозиционном зондировании селекция
волновых векторов по направлениям определяется отражением диаграммы направленности
антенны на область волновых векторов. Абсолютные значения волновых векторов,
участвующих в рассеянии определяется отдельно эффективным ядром 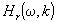 .
Ее ширина по
.
Ее ширина по  и k полностью
определяется полосами сигнала и приемного окна и при узкополосных сигнале и
окне ядро также является узкополосным. Таким образом, эффективное ядро он выделяет
узкие области волновых векторов
и k полностью
определяется полосами сигнала и приемного окна и при узкополосных сигнале и
окне ядро также является узкополосным. Таким образом, эффективное ядро он выделяет
узкие области волновых векторов  ,
дающих основной вклад в рассеянный сигнал.
,
дающих основной вклад в рассеянный сигнал.
Сформулируем характерные селективные свойства рассеяния, которые следуют из спектрального представления рассеянного сигнала (6).
-
Условие Вульфа-Брэгга: основной вклад в рассеяние дают пространственные гармоники с волновыми векторами, модули которых сосредоточены в узкой области вблизи 2k0, определяющейся формой зондирующего сигнала и премного окна.
-
Условие зеркальности: основной вклад в рассеянный сигнал дают волновые вектора,
направления которых лежат в створе углов, определяемом зеркальным отражением
диаграммы направленности (в
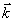
-пространстве).
Область применимости полученного выражения для рассеянного сигнала (6) более подробно обсуждалось в [6] и совпадает с условием дальней зоны приемно-передающей антенны, которое является ограничением области применимости исходной формулы (1). Таким образом, выражение (6) является аналогом исходной формулы (1) в спектральной области без дополнительных ограничений на область применимости.
2.Интерпретация одиночных спектров рассеянного сигнала.
Основной вклад в рассеянный сигнал дают пространственные гармоники среды близкие к удвоенному волновому числу зондирующей волны. Этот факт в статистической постановке задачи рассеяния в случайных средах хорошо известен[1,2]. В линейной постановке задачи рассеяния от флуктуаций диэлектрической проницаемости среды это было показано выше.
Часто, при построении моделей среды, в качестве модели берут набор независимых рассеивателей-частиц [2,7]. Этот подход хорош для определения таких характеристик отдельного рассеивателя, как положение и скорость(например в случае радиолокации), но такую огромную среду, какой является ионосфера, трудно охарактеризовать малым набором дискретных малых рассеивателей и определить их свойства. Это связано с тем, что в случае распределенной цели основной вклад в рассеянный сигнал должны давать достаточно протяженные пространственные структуры. Поэтому, в качестве модели выберем набор независимых пространственных гармоник.
Предлагаемая модель основана на следующих предположениях:
- Основной вклад в рассеянный сигнал дают пространственные гармоники среды, волновые числа которых распределены дискретно.
- Каждая пространственная гармоника обладает спектром колебаний, отличаясь временем начала этого колебания, его амплитудой и фазой.
Аналитически модель среды можно представить в виде:
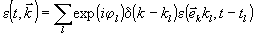 (8)
(8)
здесь 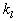 - дискретный набор пространственных гармоник;
- дискретный набор пространственных гармоник; 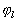 - начальная фаза для l-ой
пространственной решетки;
- начальная фаза для l-ой
пространственной решетки; 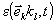 - зависимость l-го
пространственного спектра флуктуаций от направления волнового вектора,
- зависимость l-го
пространственного спектра флуктуаций от направления волнового вектора, 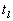 - время начала колебания l-ой
пространственной гармоникой.
- время начала колебания l-ой
пространственной гармоникой.
Уникальным в этой модели является лишь предположение о дискретности волновых векторов, дающих основной вклад в рассеяние. Спектр колебаний выделенной пространственной гармоники может быть предсказан на основе существующих моделей среды: либо на основе дисперсионного уравнения[8,9], связывающему волновой вектор пространственной решетки со спектром ее собственных колебаний, либо на основе кинетического рассмотрения [7,10].
Таким образом, исходя из радиолокационного уравнения (6) модельный спектр рассеянного сигнала представим в виде:
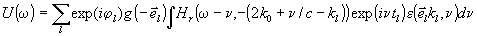 (9)
(9)
Как хорошо видно, неизвестными параметрами данной модели, подлежащими определению
являются время возникновения колебания 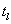 ,
волновое число колебания
,
волновое число колебания 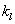 и начальная фаза
и начальная фаза 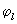 .
.
В случае, когда спектр колебаний значительно шире ядра 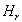 ,
что выполняется в большинстве экспериментов
по измерению формы спектров рассеянного сигнала, модель (9) можно значительно
упростить:
,
что выполняется в большинстве экспериментов
по измерению формы спектров рассеянного сигнала, модель (9) можно значительно
упростить:
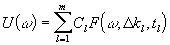 (10)
(10)
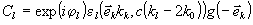 (11)
(11)
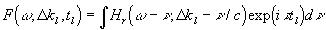 (12)
(12)
где 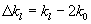 - отличие волнового числа пространственной гармоники среды от удвоенного волнового
вектора зондирующего сигнала.
- отличие волнового числа пространственной гармоники среды от удвоенного волнового
вектора зондирующего сигнала.
В качестве алгоритма поиска параметров модели использовался аналог методики, предложенной в [11], основа которого состоит в последовательной оценке параметров наиболее мощного компонента суммы (9) методом наименьших квадратов, его вычитании и аналогичному анализу оставшейся части.
В качестве исходных данных были взяты данные полученные методом НР во время ионосферных бурь 25 сентября 1998 года (Иркутск) и 13 ноября 1998 года(Милстон-Хилл), когда отношение сигнал/шум было достаточно высоко (порядка 5-10). Большое отношение сигнал/шум было необходимо для большего доверия полученным данным.
При анализе выполнялись следующие положения:
- Временное окно полагалось равным сигналу по форме (прямоугольной) и длительности.
- В качестве модели использовалась упрощенная модель (10) - спектр зондирующего сигнала значительно уже частотного спектра флуктуаций.
- Убыванием мощности сигнала с расстоянием пренебрегалось в целях упрощения
записи для эффективного ядра
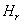
.
В этих приближениях эффективное ядро можно записать в виде:
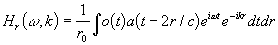 (13)
(13)
где 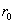 - центр объема, выделяемого пересечением зондирующего сигнала и окна.
- центр объема, выделяемого пересечением зондирующего сигнала и окна.
Тогда модельные функции 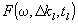 разложения (10) могут быть записаны в виде:
разложения (10) могут быть записаны в виде:
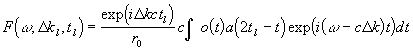 (14)
(14)
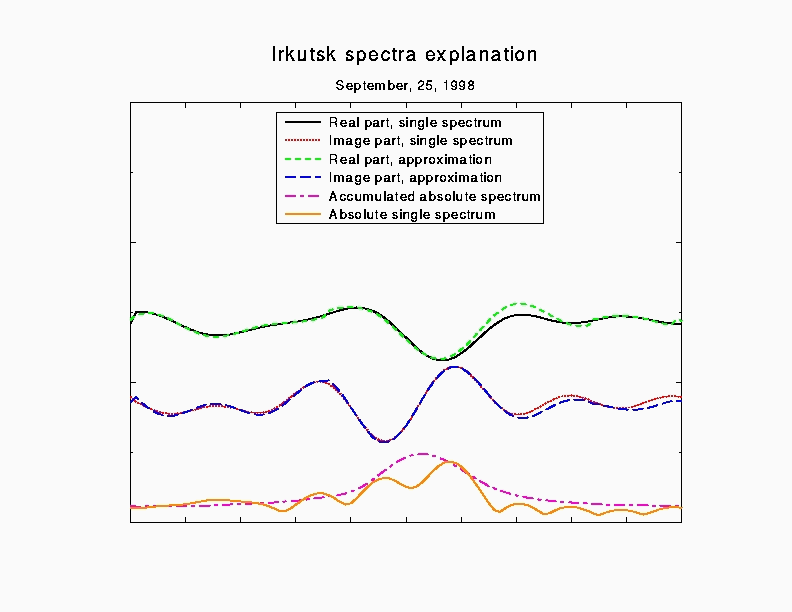
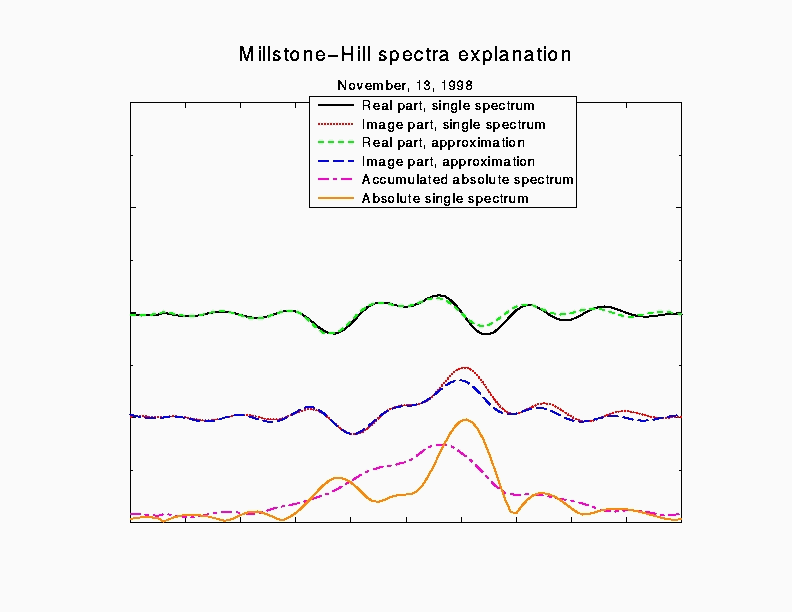
Результаты расчетов приведены на рис.1-3. На рис.1-2. показано, что спектры в отдельной реализации, вообще говоря, не повторяют накопленную спектральную мощность, а имеют вид нескольких “сдвинутых” линий, что качественно объясняется предложенной моделью рассеяния на дискретных периодических решетках. На этих рисунках также показано высокое качество подгонки одиночных спектров моделью рассеяния на десяти пространственных гармониках.
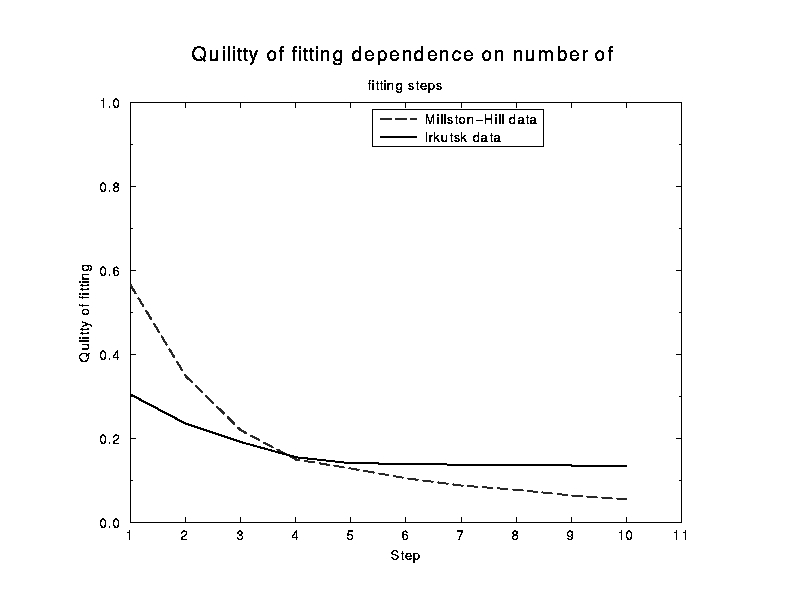
На рис.3. показано обычное качество подгонки (энергетики части спектра, не укладывающейся в предложенную модель), нормированное на мощность исходного спектра. Видно, что эта величина быстро убывает с числом модельных периодических структур, что позволяет надеяться на удачность предложенной модели для описания спектра рассеянного сигнала. Видно, что окончательное качество подгонки (для десяти пространственных гармоник) для данных Милстон-Хилла лучше, чем для Иркутских, что может быть связано в первую очередь, с более высоким отношением сигнал/шум на данных радара Милстон-Хилл.
|
|
|
|
Рис.1. Формы спектров иркутского радара НР и результаты подгонки.
Сверху вниз: Действительная часть спектра и модель; Мнимая часть спектра и модель; Спектральная мощность одной реализации и накопленная спектральная мощность |
Рис.2. Формы спектров и результаты подгонки дли радара Миллстон-Хилл.
Сверху вниз: Действительная часть спектра и модель; Мнимая часть спектра и модель; Спектральная мощность одной реализации и накопленная спектральная мощность |
|
|
|
Рис.3. Качество подгонки в зависимости от числа учитываемых пространственных гармоник. |
Заключение.
В главе изложен метод получения взаимосвязи рассеянного сигнала со спектральными характеристиками среды, суть которого состоит в переходе к рассмотрению рассеяния на пространственных гармониках среды и применению метода стационарной фазы для вычисления вкладов отдельных гармоник.
На основе предложенного метода получено радиолокационное уравнения для спектра рассеянного сигнала (6) без ограничений на размеры зондируемого объема и радиус корреляции неоднородностей. Оно в явном виде показывает селективный характер процесса рассеяния: основной вклад в рассеяние дают пространственные гармоники среды, для которых выполняются условия Вульфа-Брэгга(4) и зеркальности. Полученные уравнения являются аналогом соответствующих радиолокационных уравнений для рассеяния на малом рассеивающем объеме[2-3], но получены без предположения о малости рассеивающего объема.
Полученные уравнения были использованы для построения модели(10-12) и предварительного анализа непосредственно спектров сигналов рассеяния, без перехода к их среднеквадратичным характеристикам. Предложенная модель рассеяния на дискретных периодических решетках и полученное радиолокационное уравнение для спектров рассеянного сигнала качественно объясняет форму спектра рассеянного сигнала в одной реализации и может применяться для количественных расчетов точных значений волновых векторов на которых идет наиболее эффективное рассеяние и времен возникновения колебаний этих пространственных решеток.
Применение методики для объяснения одиночных спектров Иркутского радара НР и Радара НР Милстон-Хилл показало ее эффективность и способность качественного и количественного объяснения получаемых данных без перехода к среднеквадратичным характеристикам.
Данная методика может использоваться на большинстве радаров, диагностирующих атмосферу и ионосферу методом обратного рассеяния радиоволн.
Благодарности. Авторы благодарны Орлову И.И. за информативное обсуждение. Также авторы благодарны Ф. Эриксону за любезно предоставленные данные радара НР Милстон-Хилл.
Литература
- В.И. Татарский, Распространение волн в турбулентной атмосфере. М., Наука, 1967, 548с
- А. Исимару Распространение и рассеяние волн в случайно-неоднородных средах. в 2-х томах, М.Мир,1981.
- Р. Ньютон, Теория рассеяния волн и частиц.М.,Мир.,1969,607с
- Wanberg G.,Wastman A., Pellien-Wannberg A., Three-dimensional head echo cross-sections at 931MHz measured by EISCAT. //тезисы докладов USNC/URSI, Boulder, 1999, 230.
- Федорюк М.В. Ассимптотика:интегралы и ряды М.,Наука,-1987-544с
- О.И. Бернгардт., А.П. Потехин, К теории рассеяния радиосигналов в атмосфере, Оптика атмосферы и океана, 10, N12(1997), с.1513-1516.
- Дж. Шеффилд, Рассеяние электромагнитного излучения в плазме,-М.,Наука,1978,279с.
- O. Buneman, Excitation of field alligned sound waves by electron streams, Phys.Rev.Lett.,10,285-287,1963.
- D.T. Farley, A plasma instability resulting in field-alligned irregularities in the ionosphere, JGR, 68, 6083-6097, 1963.
- A.M. Hamza, J.-P.St-Maurice, A turbulent theoretical framework for the study of current-driven E region irregularities at high latitudes: basic derivation and application to gradient-free situations,JGR,1993,11587-11599.
Г.В. Куклин, И.И. Орлов, О.И. Бернгардт, О методике определения периодичностей на примере анализа чисел Вольфа., Исследования по геомагнитизму, аэрономии и физике солнца, в печати.

