О ЗАКОНОМЕРНОСТЯХ ДВИЖЕНИЯ ВОДЫ И НАНОСОВ В ЕСТЕСТВЕННЫХ РУСЛОВЫХ ПОТОКАХ
А.В. Хон
Институт Оптического Мониторинга СО РАН, Томск
Из характеристики турбулентного движения следует, что мгновенные скорости речного потока непрерывно меняются в каждой точке. Но, если измерение скорости в точках потока производить длительное время (несколько минут), то можно получить осредненную скорость течения воды в этой точке. Осредненное по времени значение продольной составляющей скорости течения является более устойчивой величиной, для того чтобы ориентироваться на нее при определении воздействия потока воды на подстилающий грунт. Частицы воды, соприкасаясь с поверхностями дна и берегов, смачивают их и становятся неподвижными. В этом случае можно говорить о нулевых скоростях у дна и берегов. Но, как показали гидрометрические измерения, это положение не всегда верно. Скорости у дна и берегов могут быть соизмеримы с поверхностной скоростью на динамической оси потока (до 2/3 от поверхностной). Слой, в пределах которого скорость возрастает до соизмеримых скоростей с поверхностной, называется пограничным слоем. Как правило, пограничный слой имеет небольшую толщину в сравнении с шириной или глубиной речного потока. Поэтому многие исследователи вполне обоснованно принимают скорость на верхней границе пограничного слоя за донную или пристеночную скорости турбулентного речного потока.
Поскольку речной поток всегда является по меньшей мере двухфазным (состоит из двух компонент: движущаяся вода и переносимый ею твердый материал), возникает вопрос о распределении концентрации твердых частиц в этом потоке. Твердый обломочный материал (наносы или аллювий) появляется в потоке как результат взаимодействия текущей водной среды с поверхностными частицами грунта.
Несимметричность обтекания водой частиц проявляется в превышении скорости выше частицы над скоростью под частицей. Кроме того, на грань твердой частицы. обращенную на встречу течения жидкости будет действовать сила лобового сопротивления, а с тыльной стороны частицы возникает область пониженного давления. В областях пониженного давления возникают вихри, которые захватывают оторванную от дна частицу внутрь себя и поднимают ее в толщу потока. Условия взвешивания твердых частиц определяется гидравлическим режимом, от которого зависит взаимодействие потока с руслом, а также составом его дна, т.е. геометрической и гидравлической крупностью наносов.
Предлагаемый нами подход к исследованию процессов перемещения донных наносов, основывается на использовании моделей Н.Е. Жуковского, Н.М. Бочкова, Ц.Е. Мирцхулавы, Г.В. Железнякова, Ю.Л. Пейча и др. для начальной стадии деформации речных русел. Оказалось, что такой подход можно реализовать и к исследованиям перемещения донных наносов. Полученные результаты представляют экологический интерес, так как частицы вредных примесей, оседая на дно, прилипают к частицам обломочного материала, переносимого рекой, и перемещаются вдоль реки вместе с ними.
1.Распределение скоростей по вертикали руслового потока
Для удовлетворения нужд практики различными исследователями были предложены эмпирические и полуэмпирические формулы распределения скоростей по вертикали плоского потока.
При гидравлическом анализе русловых потоков (перемешивание потоков, движения наносов и деформации русел) используются формулы изменения скоростей по вертикали, предложенные Р. Ясмундом, А.В. Караушевым и др. [1]. Они в равной мере удовлетворяют эмпирическим данным и не имеют особых преимуществ друг перед другом. Однако для каждой из этих формул требуется информация о шероховатости дна на каждой выбранной в живом сечении вертикали. Поэтому подойдем к распределению скоростей по вертикали иначе.
Рассмотрим трехмерное уравнение вида
 (1)
(1)
где A - коэффициент турбулентного
обмена, C - коэффициент Шези, I - уклон водной поверхности,
i - уклон дна и т.д. Используем гипотезу В.М. Маккавеева,
что A=Kv и подставим величину A в вышестоящее уравнение. Тогда
получим: 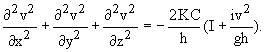 Произведя замену
Произведя замену 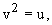 получим
получим
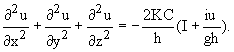 (2)
(2)
Полагая  в уравнении (2),
получим уравнение распространения скоростей в живом сечении
в уравнении (2),
получим уравнение распространения скоростей в живом сечении
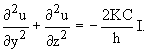 Полагая
Полагая 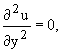 получим уравнение распределения скоростей в продольном вертикальном
сечении речного потока
получим уравнение распределения скоростей в продольном вертикальном
сечении речного потока
 (3)
(3)
Координата (x) направлена вдоль потока, координата (y) отсчитывается от динамической оси потока по направлению к берегу, координата (z) - от поверхности ко дну. Можно рассматривать и одномерные распределения продольных скоростей по вертикали
 (4)
(4)
с граничными условиями на концах осевой вертикали. Для иллюстрации предлагаемой нами методики, приведем пример расчета скоростей руслового потока по глубине на одной из заданных вертикалей по граничным данным, описанным в работе [3].
Пример 1. Найти распределение
продольных скоростей по вертикали с граничными условиями:
при z=0 u=0.020736; z=h=0.3 u=0.0784;
C=17.75; I=0.0004; K=0.7C+6. Обозначим E=(KCI)/h
и решим уравнение  решение которого будет иметь общий вид:
решение которого будет иметь общий вид: 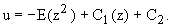 Используя граничные условия, найдем решение этого уравнения:
Используя граничные условия, найдем решение этого уравнения:
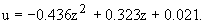
|
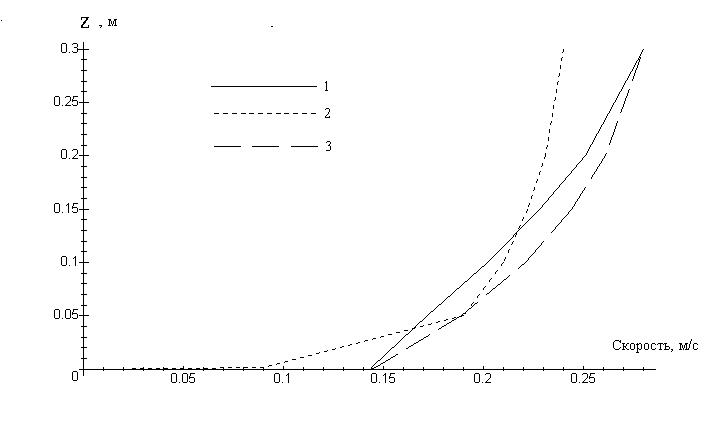
|
|
Рис. 1 (1 - фактическая скорость, 2 - скорость по Гончарову, 3- вычисленная скорость) |
2.Распределение скоростей по живому сечению руслового потока
Под площадью живого сечения руслового потока понимается часть площади его поперечного сечения, в котором скорости течения больше предела чувствительности прибора измерения скоростей.
Вопрос о распределении продольных скоростей в живом сечении турбулентного потока находится с давних пор в поле зрения исследователей в области гидравлики и гидрометрии и до настоящего времени является одной из основных задач гидромеханики. Вышеуказанные формулы распределения скоростей по вертикали речного потока дают возможность в некоторой степени судить о распределении только на средней вертикали речного потока или на любой одной вертикали по ширине русла. Но они не дают возможности разрешить одну из основных проблем гидравлики, а именно, определение средней скорости потока и расхода. Чтобы решить эту задачу с помощью вышеуказанных полуэмпирических формул, кроме глубины на каждой выделенной вертикали требуется знать еще хотя бы один параметр (средняя или поверхностная скорость, коэффициент шероховатости и т.п.). Уместно заметить также, что не менее важной является задача о распределении скоростей вдоль продольного профиля речного потока.
В работах [4, 5] рассмотрены распределения скоростей для прямоугольного и треугольного видов каналов. Но они имеют ряд существенных недостатков. Учитывая недочеты работ [4, 5], улучшим расчеты распределения продольных скоростей в живом сечении.
Учитывая сказанное в предыдущем пункте, распределение продольных скоростей в живом сечении, будет описываться уравнением
 ;
; ,
(5)
,
(5)
где  -
граничные условия по периметру живого сечения
-
граничные условия по периметру живого сечения 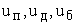 - скорости на поверхности, у дна осевой вертикали и у берега.
Будем полагать, что живое сечение имеет форму прямоугольника.
В этом случае, измеряя значения продольных скоростей в ряде
точек на водной поверхности и у дна, а также вычисляя распределение
продольных скоростей на оси потока и у берегов по описанному
выше уравнению, получим граничные условия для решения уравнения
Пуассона.
- скорости на поверхности, у дна осевой вертикали и у берега.
Будем полагать, что живое сечение имеет форму прямоугольника.
В этом случае, измеряя значения продольных скоростей в ряде
точек на водной поверхности и у дна, а также вычисляя распределение
продольных скоростей на оси потока и у берегов по описанному
выше уравнению, получим граничные условия для решения уравнения
Пуассона.
Задача, определяемая
уравнениями (3) и (4) является задачей Дирихле (первой краевой
задачей). Величину 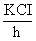 обозначим через E. Тогда уравнение (5) примет вид:
обозначим через E. Тогда уравнение (5) примет вид: 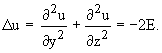 Для численного решения задачи Дирихле уравнения Пуассона довольно
часто используют конечноразностные методы [6] Сделаем попытку
получить распределение скоростей по живому сечению иным образом.
Для численного решения задачи Дирихле уравнения Пуассона довольно
часто используют конечноразностные методы [6] Сделаем попытку
получить распределение скоростей по живому сечению иным образом.

Будем считать, что скорости
от осевого сечения в направлении ко дну и берегу убывают.
Используя известное распределение скоростей по осевой вертикали
 т.е.
т.е.
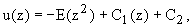 где
где
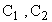 -
неизвестные константы, находящиеся из граничных условий. Эти
величины равны:
-
неизвестные константы, находящиеся из граничных условий. Эти
величины равны:  где
где 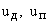 - донная и поверхностная скорости на оси потока. Для решения
уравнения Пуассона используем метод разделения переменных.
Решение уравнения Пуассона
- донная и поверхностная скорости на оси потока. Для решения
уравнения Пуассона используем метод разделения переменных.
Решение уравнения Пуассона  для живого сечения будем искать в виде:
для живого сечения будем искать в виде:  Подставляя в предыдущее уравнение решение одномерного уравнения
u(z), получим
Подставляя в предыдущее уравнение решение одномерного уравнения
u(z), получим  Считая, что в этом случае u(z) - величина постоянная, найдем
Считая, что в этом случае u(z) - величина постоянная, найдем
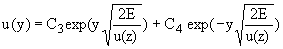 ,
(6)
,
(6)
где 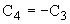 ,
так как
,
так как  ,
,
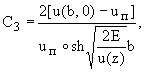 где b -полуширина речного русла; u(b, 0) - поверхностная скорость
у берега. Таким образом,
где b -полуширина речного русла; u(b, 0) - поверхностная скорость
у берега. Таким образом,
 (7)
(7)
3. Распределение скоростей по продольному вертикальному профилю руслового потока
Рассмотрим решение уравнения (3), которое запишем в виде:
 (8)
(8)
Обозначим величину 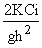 через B. Тогда уравнение (8) примет вид
через B. Тогда уравнение (8) примет вид
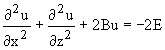 (9)
(9)
c добавлением граничных условий. Это уравнение Гельмгольца с постоянными коэффициентами при неизвестной функции u и постоянной правой частью. Для решения такого вида уравнения можно использовать конечноразностные схемы [6].
Применим метод разделения
переменных для решения задачи Дирихле уравнения типа Гельмгольца
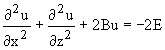 .
Решим, как и ранее, уравнение
.
Решим, как и ранее, уравнение 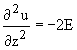 .
Получим решение в виде:
.
Получим решение в виде: 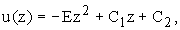 где величины
где величины 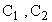 находятся
из граничных условий по вертикали, т.е.
находятся
из граничных условий по вертикали, т.е.  .
. Решение
уравнения
Решение
уравнения 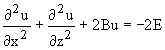 будем искать в виде u(x,z)=u(x)u(z).
Подставляя это выражение в исходное уравнение, получим после
упрощения:
будем искать в виде u(x,z)=u(x)u(z).
Подставляя это выражение в исходное уравнение, получим после
упрощения: 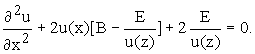 (10)
(10)
Рассмотрим три случая нахождения u(x):
1-й случай - выражение в квадратных скобках меньше нуля, тогда
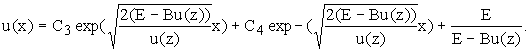 (11)
(11)
2-й случай - выражение в квадратных скобках больше нуля, тогда
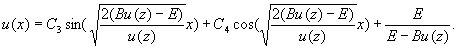 (12)
(12)
3-й случай - выражение в скобках равно нулю, тогда
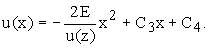 (13)
(13)
Произвольные константы
 находятся из граничных условий
находятся из граничных условий
4. Результаты расчетов
Результаты расчетов распределения скоростей по живому сечению речного русла с использованием аналитического решения для прямоугольного сечения практически совпадают с расчетами, найденными конечноразностным методом (таблица 2) и с вычислениями работы [7] (табл.1). Отличие аналитического способа от известных состоит в том, что данный способ решения уравнения Пуассона сводится к первой краевой задаче (Дирихле) с измерениями в трех-четырех граничных точках (поверхность на осевой вертикали, дно на осевой вертикали и свободная поверхность потока у берега). Решение является аналитическим и возможно его использование в речных системах с различными формами русел, например, в случае параболического или трапецеидального сечений. Все рассмотренные выше формулы для расчета распределения скоростей были реализованы в пакете программ Mathcad 7. Подобные величины продольных скоростей при таком небольшом уклоне могут наблюдаться на укрепленном участке русла ниже плотины, где движение осуществляется не только под действием продольной составляющей силы тяжести, но и под напором поступающих с верхних участков водных масс.
Таблица 1
Результаты расчетов распределения скоростей по живому сечению речного русла с использованием формулы из работы [7] для прямоугольного сечения
|
Y |
0.00 |
0.25 |
0.50 |
0.75 |
1.00 |
1.25 |
1.50 |
1.75 |
|
Z |
Скорость u , м/с |
|
0.00 |
2 |
1.968 |
1.875 |
1.719 |
1.5 |
1.219 |
0.875 |
0.469 |
|
0.25 |
1.916 |
1.886 |
1.797 |
1.647 |
1.438 |
1.169 |
0.84 |
0.451 |
|
0.50 |
1.832 |
1.803 |
1.718 |
1.575 |
1.376 |
1.12 |
0.805 |
0.433 |
|
0.75 |
1.748 |
1.72 |
1.64 |
1.504 |
1.314 |
1.07 |
0.7 |
0.415 |
|
1.00 |
1.664 |
1.637 |
1.561 |
1.432 |
1.253 |
1.021 |
0.735 |
0.397 |
|
1.25 |
1.58 |
1.555 |
1.483 |
1.361 |
1.191 |
0.971 |
0.735 |
0.379 |
|
1.50 |
1.496 |
1.472 |
1.404 |
1.289 |
1.129 |
0.872 |
0.631 |
0.361 |
|
1.75 |
1.411 |
1.389 |
1.326 |
1.218 |
1.067 |
0.921 |
0.606 |
0.343 |
Таблица 2.
Результаты расчетов распределения скоростей по живому сечению речного русла с использованием конечно-разностной схемы для прямоугольного сечения
|
y |
0.00 |
0.25 |
0.50 |
0.75 |
1.00 |
1.25 |
1.50 |
1.75 |
|
z |
Продольная скорость u , м/с |
|
0.00 |
2.00 |
1.968 |
1.875 |
1.719 |
1.5 |
1.219 |
0.875 |
0.469 |
|
0.25 |
1.916 |
1.88 |
1.796 |
1.663 |
1.481 |
1.247 |
0.944 |
0.451 |
|
0.50 |
1.832 |
1.798 |
1.721 |
1.602 |
1.442 |
1.232 |
0.947 |
0.433 |
|
0.75 |
1.748 |
1.719 |
1.648 |
1.539 |
1.392 |
1.2 |
0.926 |
0.415 |
|
1.00 |
1.664 |
1.641 |
1.576 |
1.475 |
1.337 |
1.164 |
0.893 |
0.397 |
|
1.25 |
1.58 |
1.563 |
1.503 |
1.406 |
1.273 |
1.097 |
0.849 |
0.379 |
|
1.50 |
1.496 |
1.481 |
1.423 |
1.325 |
1.191 |
1.015 |
0.778 |
0.361 |
|
1.75 |
1.411 |
1.389 |
1.326 |
1.218 |
1.067 |
0.872 |
0.631 |
0.343 |
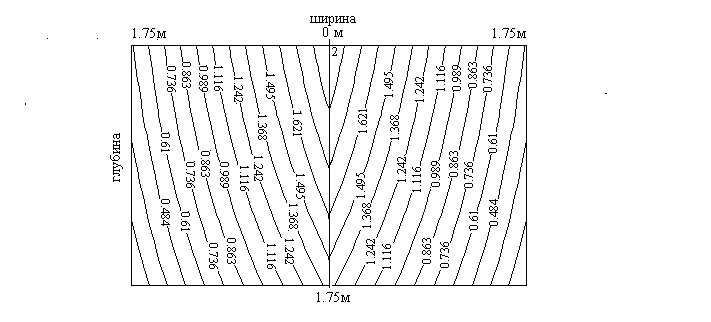
Примечание: в таблицах (1,2 ) приведены значения скорости течения в половине рассматриваемого русла, причем h=1,75м - глубина потока; b=1,75м - полуширина живого сечения; уклон русла принят равным I=0.0001; y- поперечная координата, а z- координата по глубине. Картина скоростей течения в другой половине русла предполагается симметричной в случае симметричного поперечного профиля русла. Таким образом, изолинии равных скоростей течения во всем поперечном сечении будут выглядеть как показано на рис.2.
|
|
|
Рис.2 Изотахи построенные по расчетам аналитическог метода |
Таким образом, используя уравнение Рейнольдса совместно с гипотезой В.М. Маккавеева и разрешая его методом разделения переменных, возможно добиться удовлетворительных расчетов распределения скоростей по вертикали, живому сечению и вдоль продольного профиля речного русла в сравнении с известными для равномерного установившегося водного потока в мало извилистом русле, имеющего большую ширину и сохраняющего приближенное постоянство глубины по ширине.
5. Перенос взвешенных наносов
Имеются две гипотезы
относительно переноса взвешенных наносов. Одна из них называется
диффузионной теорией, а другая гравитационной теорией переноса
частиц [3, 4].
Рассмотрим диффузионную теорию. Диффузионная теория взвешивания
наносов в турбулентном потоке получила название по аналогии
с молекулярной диффузией, которая осуществляет в ламинарном
потоке передачу скоростей и теплоты. Применение диффузионной
теории основано на аналогии между турбулентной диффузией наносов
и жидкости; при этом принимается равенство пульсаций скоростей
течения жидкости и наносов,т.е. их . коэффициенты турбулентного
обмена одинаковы. На турбулентный перенос накладывается падение
частиц, движущихся со скоростью w. Впервые диффузионная теория,
для решения вопросов о транспоте наносов потоком, была применена
В.М. Маккавеевым. Диффузионная теория взвешивания исходит
из представления того, что перенос частиц наносов в турбулентном
потоке осуществляется хаотическими, многочисленными, но малыми
по величине пульсациями. Несмотря на то, что оценки границы
области применимости диффузионной теории и ее недостатки подробно
описаны в ряде работ, например, в работах [3], необходимо
об этом сказать следующее. Как показывают эксперименты , выводы
диффузионной теории справедливы для частиц для частиц не более
0,2 мм, т.е.только мелкие взвешенные частицы могут иметь скорость
и пульсации, не отличающиеся от скорости речного потока. Для
решения вопросов взвешивания частиц в диффузионной теории
возьмем соответствующее уравнение диффузии для вертикальной
концентрации частиц, которое можно записать в виде [3]:
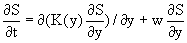 ,
(14)
,
(14)
где S- концентрация, K(y) - коэффициент диффузии, w - скорость оседания частиц. Будем сначала искать решение стационарного уравнения:
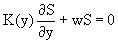 (15)
(15)
Большинство авторов избегает использовать нестационарное уравнение (14) ввиду сложности решения этого уравнения. Ниже предлагается простой способ его решения основанный на использовании ортогональных дискретных преобразований Фурье. Этот способ состоит в том, что сначала находится решение стационарного уравнения в виде ряда Фурье, а затем находятся выражения для коэффициентов этого ряда как функций времени. Решение нестационарного уравнения следует из обратного преобразования Фурье, использующего коэффициенты преобразования Фурье, зависящие от времени. Это уравнение по существу является уравнением неразрывности, так как убыль, вызванная оседанием частиц (Sw), компенсируется другой величиной - восполнением за счет частиц, переносимых вверх благодаря турбулентности. Отсюда следует, что K(y) - коэффициент турбулентного переноса частиц. Интегрируя уравнение (15), получаем
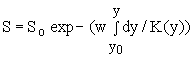 (16)
(16)
где So - концентрация частиц наносов при y=yo. Теперь задача состоит в выборе выражения для K(y). Можно воспользоваться формулой
 (17)
(17)
где  - плотность жидкости,
- плотность жидкости,
 - осредненная по времени скорость на высоте y, s
- турбулентное касательное напряжение. Довольно часто предполагают,
что напряжение s
представляет линейную функцию от глубины, т.е.
- осредненная по времени скорость на высоте y, s
- турбулентное касательное напряжение. Довольно часто предполагают,
что напряжение s
представляет линейную функцию от глубины, т.е.
 ,
(18)
,
(18)
где 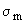 - максимальное
напряжение у дна (у=0), а h - полная глубина реки. Таким образом,
- максимальное
напряжение у дна (у=0), а h - полная глубина реки. Таким образом,
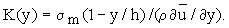 (19)
(19)
Можно использовать логарифмический закон
Кармана распределения скорости потока по вертикали y, но в
этот закон плохо применим в случае, когда y=0 или y=h. Поэтому
используем законы распределения скоростей потока по Гончарову
[2]  ,
где v - средняя по вертикали скорость потока, D
- шероховатость дна, h - глубина, y - расстояние от дна. Подставляя
эту зависимость в формулу А.Е. Шайдеггера для коэффициента
турбулентного обмена, получим выражение для концентрации наносов
в точке на вертикали.
,
где v - средняя по вертикали скорость потока, D
- шероховатость дна, h - глубина, y - расстояние от дна. Подставляя
эту зависимость в формулу А.Е. Шайдеггера для коэффициента
турбулентного обмена, получим выражение для концентрации наносов
в точке на вертикали.
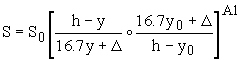 ,
где
,
где  . (20)
. (20)
Рассмотрим нестационарный случай решения уравнения (14). Так как уравнение является параболическим, то его решение на слое t1=t0+D
t может определено, если известно его решение на слое t= t0. Дискретное преобразование Фурье от уравнения (14) представим в виде:
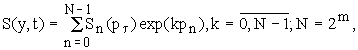 (21)
(21)
где m
- целое натуральное число, величины 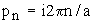 ,
,
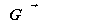 ,
,
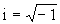 ;
a - величина по вертикали y; T - отрезок времени; число точек
деления по переменной t равно L, т. е.
;
a - величина по вертикали y; T - отрезок времени; число точек
деления по переменной t равно L, т. е. 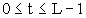 .
За начальные коэффициенты
.
За начальные коэффициенты 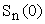 можно взять коэффициенты Фурье стационарного решения выражения
(21).
Уравнение (14)
преобразуем к виду:
можно взять коэффициенты Фурье стационарного решения выражения
(21).
Уравнение (14)
преобразуем к виду:
 (22)
(22)
Подставляя выражение (22) в уравнение (23), получим:
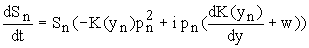 .
(23)
.
(23)
Из решения уравнения (24) следует, что
 (24)
(24)
Решение S(t0+D
t) следует из обратного
преобразования Фурье, использующего известные коэффициенты
преобразования Фурье на предыдущем слое. Точное нахождение
концентрации наносов имеет смысл, так как она используется
для отыскания количества расходов взвешенных наносов. Например,
по вертикали речного потока формула удельного расхода взвешенных
расходов имеет вид: 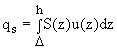 ,
где h - глубина;
,
где h - глубина; 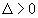 - величина над дном - начала отсчета взвешенных наносов; S(z)
- концентрация наносов по вертикали; u(z) - скорость по вертикали
речного потока.
- величина над дном - начала отсчета взвешенных наносов; S(z)
- концентрация наносов по вертикали; u(z) - скорость по вертикали
речного потока.
6. Перемещение донных наносов
Используем понятие начальной
неразмывающей скорости 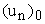 на вертикали y, как скорости, при значениях меньше которой
частицы не могут прийти в движение. Динамическое уравнение
движения частицы при подъеме ее со дна в направлении оси y
можно записать в виде :
на вертикали y, как скорости, при значениях меньше которой
частицы не могут прийти в движение. Динамическое уравнение
движения частицы при подъеме ее со дна в направлении оси y
можно записать в виде :
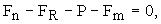 (25)
(25)
где 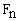 -
подъемная сила,
-
подъемная сила,  -
сила сопротивления воды, P - вес частицы в воде,
-
сила сопротивления воды, P - вес частицы в воде,  сила
инерции,
сила
инерции,  масса
частицы, d - диаметр фракций донных наносов,
масса
частицы, d - диаметр фракций донных наносов, 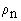 -
плотность частицы наносов,
-
плотность частицы наносов,  -
ускорение частицы,
-
ускорение частицы,  -
скорость частицы в направлении оси y, t - время [8].
-
скорость частицы в направлении оси y, t - время [8].
Входящие в уравнение (26) силы могут быть выражены:
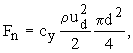
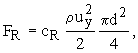
 (26)
(26)
где  -
коэффициент подъемной силы; r
- плотность воды,
-
коэффициент подъемной силы; r
- плотность воды, 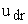 -
донная размывающая скорость воды, при которой вероятность
отрыва частиц от дна больше нуля,
-
донная размывающая скорость воды, при которой вероятность
отрыва частиц от дна больше нуля, 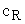 -
коэффициент лобового гидродинамического сопротивления.
-
коэффициент лобового гидродинамического сопротивления.
Будем рассматривать отдельно движение донных наносов как скачкообразно, так и путем качения.
Сначала рассмотрим способ
качения. Как следует из работы [8], в этом случае сила 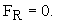 Сила P (согласно статистической механики) из уравнения (26)
разлагается на силу Psin
Сила P (согласно статистической механики) из уравнения (26)
разлагается на силу Psin и силу
и силу  ,
где c - коэффициент
сцепления грунта,
,
где c - коэффициент
сцепления грунта, 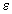 -
коэффициент трения, а
-
коэффициент трения, а 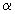 -
угол, образуемый дном русла и горизонтальной плоскостью. Уравнение
движения частицы можно получить обычным способом, приравнивая
все силы, действующие в направлении руслового потока, к произведению
массы частицы на ускорение, т.е.;
-
угол, образуемый дном русла и горизонтальной плоскостью. Уравнение
движения частицы можно получить обычным способом, приравнивая
все силы, действующие в направлении руслового потока, к произведению
массы частицы на ускорение, т.е.;  .
Так как уравнение движения рассматривается только одной частицы,
то в выражение для силы Q коэффициент сцепления грунта c входит
не будет. В этом случае уравнение (26) примет вид:
.
Так как уравнение движения рассматривается только одной частицы,
то в выражение для силы Q коэффициент сцепления грунта c входит
не будет. В этом случае уравнение (26) примет вид:
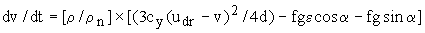 (27)
(27)
В стационарном состоянии dv/dt=0 и, таким образом,
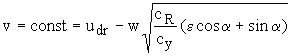 (28)
(28)
где w- гидравлическая
крупность частиц. Для нестационарного случая нужно решить
уравнение (28). Разрешая это уравнение и приравнивая скорость
частицы v нулю, можно найти время и длину пути движения частицы,
т.е. 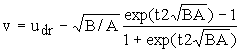 ,
где
,
где  ,
,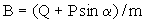 Время движения частицы равно
Время движения частицы равно 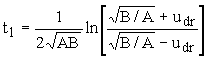 .Величина
.Величина ,
а величина
,
а величина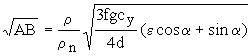 .
Длину пути движения
частицы можно вычислять по формуле:
.
Длину пути движения
частицы можно вычислять по формуле:
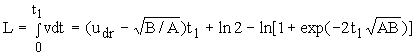 .
(29)
.
(29)
Для скачкообразного перемещения частицы уравнение (3.22) примет следующий вид:
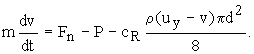 (30)
(30)
Решая уравнение (31)
и приравнивая скорость v нулю, можно найти продолжительность
и длину пути скачка. Имея скорость движения твердой частицы,
можно определить расстояние на которое переместится частица
исходя из величины донной скорости. Таким образом, обозначая
в уравнении (31) величины 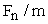 ,
,
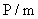 ,
,
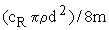 через A, B, D соответственно, а
через A, B, D соответственно, а  через z,
получим:
через z,
получим: 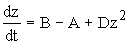 при
при 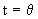 z=0, где
z=0, где 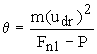 .
Начальные данные для уравнения при
.
Начальные данные для уравнения при  (время разгона частицы) y=0 , где
(время разгона частицы) y=0 , где  ;
;
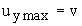 .
Положим
.
Положим 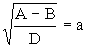 .
Тогда решение уравнения будет иметь вид:
.
Тогда решение уравнения будет иметь вид: 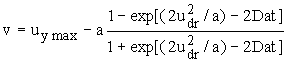 ,
где
,
где 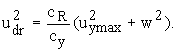 Полагая v=0, найдем время скачка
Полагая v=0, найдем время скачка 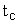 ,
которое имеет вид:
,
которое имеет вид: 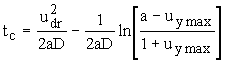 .
Обозначим через
.
Обозначим через 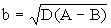 .
Тогда длину пути перемещения частицы по горизонтали можно
определить по формуле:
.
Тогда длину пути перемещения частицы по горизонтали можно
определить по формуле: 
Литература
- Чеботарев А.И. Общая гидрология.- Л.: Гидрометеоиздат, 1975.- 544 с.
- ГончаровВ.Н. Динамика русловых потоков.-Л.:Гидрометеоиздат, 1962-374с
- Россинский К.И., Дебольский В.К. Речные наносы.- М.:Наука, 1980. - 216 с.
- Назарян А.Г. О расчете изотах при равномерном турбулентном течении в прямоугольных каналах.- Труды ГГИ.- Л.:Гидрометеоиздат, 1955. - в. 49(103).- С. 34-43.
- Касьянова Н.Д. К расчету поля скоростей в русле треугольной формы.- Гидравлика и гидротехника.- Киев: Изд-во Техника, 1981.- в 32.- С. 27-31.
- Самарский А.А. Введение в численные методы.-М.: Наука, 1987.- 296 с.
- Гольдина В.Д. Метод расчета турбулентных течений в открытых потоках различной формой поперечного сечения: Дис. …канд. Физ - мат. наук.- Душанбе, 1984.- 154 с.
Желязняков Г.В., Пейч Ю.Л. Начальная стадия деформации русел //Метереология и гидрология. - 1995. - №10. - С. 77-84.

