СПОНТАННОЕ ВОЗНИКНОВЕНИЕ РЕГУЛЯРНОЙ СТРУКТУРЫ ПОВЕРХНОСТИ СТЕКАЮЩЕЙ ПЛЕНКИ ЖИДКОСТИ ПРИ НЕОДНОРОДНОМ НАГРЕВЕ
О.В. Шарыпов, К.А. Медведко
Институт теплофизики СО РАН, Новосибирский государственный университет
Изучение фундаментальных закономерностей, связанных с режимами пленочного течения представляет интерес для решения широкого круга практических задач, возникающих при проектировании и оптимизации технологических установок в энергетике, химической промышленности и других отраслях производства. Настоящая работа посвящена теоретическому изучению процессов пленочного течения жидкости по наклонной поверхности при наличии локального теплового источника.
Введение.
Экспериментальные исследования, проводимые в настоящее время в Институте теплофизики СО РАН [1], показывают, что эффекты термокапиллярности при определенных условиях могут оказывать существенное влияние на характер течения тонкой пленки. В экспериментах наблюдается возникновение “вала” жидкости в области большого градиента температуры поверхности пленки, толщина пленки на источнике тепла уменьшается, основная часть жидкости собирается в “струи”, которые образуют периодическую структуру. Самопроизвольное возникновение периодической пространственной структуры течения представляет собой новое интересное физическое явление, которое может быть объяснено и описано в рамках представлений и методов теории самоорганизации. Суть этого явления состоит в том, что при превышении критического значения управляющего параметра двумерная стационарная структура поля скорости (и температуры), определяемая гравитацией, вязкостью и градиентом поверхностного натяжения жидкости, теряет устойчивость по отношению к малым периодическим поперечным возмущениям. В работе аналитически и численно показано, что в результате совместного действия эффектов энергетической накачки длинноволновых возмущений, диссипации энергии коротковолновых возмущений и нелинейного взаимодействия гармоник система переходит к новому квазиустойчивому стационарному состоянию с более низкой пространственной симметрией. Подобный сценарий эволюции неравновесных систем универсален и характерен для очень широкого круга различных по физическим механизмам явлений. Используемый в работе подход ранее позволил создать эволюционные модели периодической структуры поверхностей раздела (фронтов) в задачах, связанных с горением и детонацией в газах, затвердеванием слабых растворов и др. [2-4].
Постановка задачи.
Рассмотрим течение пленки
вязкой теплопроводной несжимаемой (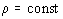 )
жидкости, имеющей толщину
)
жидкости, имеющей толщину 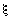 ,
по плоскости с углом наклона к вертикали
,
по плоскости с углом наклона к вертикали 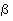 в поле тяжести (
в поле тяжести (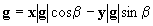 - ускорение свободного падения). Координатные оси ориентированы
следующим образом: ось x
направлена вдоль плоскости в направлении течения пленки, ось
z
направлена вдоль плоскости перпендикулярно направлению течения
пленки, ось y
направлена перпендикулярно плоскости в сторону жидкости. Жидкость
имеет температуру T,
равную температуре стенки, и соответствующее этой температуре
значение коэффициента поверхностного натяжения
- ускорение свободного падения). Координатные оси ориентированы
следующим образом: ось x
направлена вдоль плоскости в направлении течения пленки, ось
z
направлена вдоль плоскости перпендикулярно направлению течения
пленки, ось y
направлена перпендикулярно плоскости в сторону жидкости. Жидкость
имеет температуру T,
равную температуре стенки, и соответствующее этой температуре
значение коэффициента поверхностного натяжения 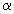 .
В решении будем пренебрегать эффектами, связанными с потоками
тепла, массы и импульса через свободную поверхность жидкости.
Давление внешней среды считается постоянным p0.
Течение пленки позволяет определить число Рейнольдса
.
В решении будем пренебрегать эффектами, связанными с потоками
тепла, массы и импульса через свободную поверхность жидкости.
Давление внешней среды считается постоянным p0.
Течение пленки позволяет определить число Рейнольдса
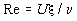 ,
где U
- скорость на поверхности пленки жидкости,
,
где U
- скорость на поверхности пленки жидкости, 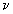 -
кинематическая вязкость. Известно [5], что на протяжении определенного
начального участка свободная поверхность пленки будет оставаться
плоской. Соответствующий профиль скорости не зависит от x
и z,
поле температуры на поверхности пленки однородно, коэффициент
поверхностного натяжения – постоянный (
-
кинематическая вязкость. Известно [5], что на протяжении определенного
начального участка свободная поверхность пленки будет оставаться
плоской. Соответствующий профиль скорости не зависит от x
и z,
поле температуры на поверхности пленки однородно, коэффициент
поверхностного натяжения – постоянный (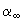 ).
Если в пределах этого участка, начиная с координаты x0=0,
на плоскости действует источник тепловыделения постоянной
мощности (имеющий бесконечную протяженность по координате
y), то в жидкости
формируется тепловой пограничный слой, возникает неоднородность
поля температуры поверхности пленки по координате x,
что приводит к наличию градиента поверхностного натяжения.
В области заметного значения градиента поверхностного натяжения
течению жидкости под действием гравитации препятствует направленная
тангенциально к свободной поверхности капиллярная сила, что
является проявлением эффекта термокапиллярной конвекции [6].
Локальное замедление течения жидкости вблизи свободной поверхности
приводит к возрастанию толщины пленки, которая оказывается
функцией градиента поверхностного натяжения (и тем самым –
координаты x:
).
Если в пределах этого участка, начиная с координаты x0=0,
на плоскости действует источник тепловыделения постоянной
мощности (имеющий бесконечную протяженность по координате
y), то в жидкости
формируется тепловой пограничный слой, возникает неоднородность
поля температуры поверхности пленки по координате x,
что приводит к наличию градиента поверхностного натяжения.
В области заметного значения градиента поверхностного натяжения
течению жидкости под действием гравитации препятствует направленная
тангенциально к свободной поверхности капиллярная сила, что
является проявлением эффекта термокапиллярной конвекции [6].
Локальное замедление течения жидкости вблизи свободной поверхности
приводит к возрастанию толщины пленки, которая оказывается
функцией градиента поверхностного натяжения (и тем самым –
координаты x:
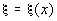 ).
Трансформация свободной поверхности приводит к установлению
нового стационарного режима, при котором термокапиллярные
силы уравновешиваются гравитацией. Расход жидкости
).
Трансформация свободной поверхности приводит к установлению
нового стационарного режима, при котором термокапиллярные
силы уравновешиваются гравитацией. Расход жидкости 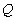 при этом оказывается постоянным (не зависит от x
при этом оказывается постоянным (не зависит от x
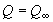 ).
Чтобы найти распределение термокапиллярной силы, необходимо
решить тепловую задачу. Однако в случае неоднородного тепловыделения
и пленочного течения аналитическое решение данной задачи найти
не удается [7], поэтому далее будем считать функции T(x)
и
).
Чтобы найти распределение термокапиллярной силы, необходимо
решить тепловую задачу. Однако в случае неоднородного тепловыделения
и пленочного течения аналитическое решение данной задачи найти
не удается [7], поэтому далее будем считать функции T(x)
и 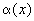 известными из эксперимента (в [1] регистрировалось поле температуры
на поверхности пленки).
известными из эксперимента (в [1] регистрировалось поле температуры
на поверхности пленки).
Решение стационарной задачи.
Для нахождения решения
поставленной задачи, т.е. получения стационарной зависимости
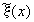 ,
необходимо решить систему уравнений Навье-Стокса с граничными
условиями на свободной поверхности (
,
необходимо решить систему уравнений Навье-Стокса с граничными
условиями на свободной поверхности (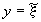 ),
на стенке (
),
на стенке (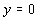 )
и условием постоянства расхода:
)
и условием постоянства расхода:
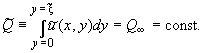 (1)
(1)
Учитывая, что толщина
слоя жидкости мала по сравнению с характерной протяженностью
неоднородности свободной поверхности по координате x,
уравнения Навье-Стокса для стационарного течения, не зависящего
от z,
можно упростить и записать в приближенной форме (2), вводя
следующие обозначения: давление 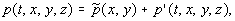 скорость
скорость 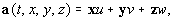 где
где 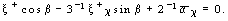
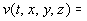
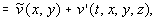
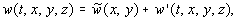
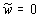 .
.
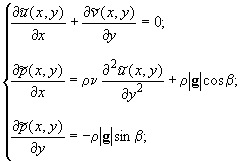 (2)
(2)
Граничное условие на свободной поверхности в общем виде [8]:
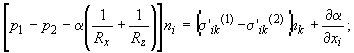 (3)
(3)
где 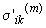 -
компоненты тензора вязких напряжений в m-той
среде,
-
компоненты тензора вязких напряжений в m-той
среде, 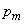 - давление в m-той
среде,
- давление в m-той
среде, 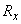 и
и 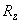 - главные радиусы кривизны свободной поверхности,
- главные радиусы кривизны свободной поверхности, 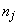 - компоненты вектора нормали
- компоненты вектора нормали 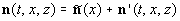 к свободной поверхности. Учитывая, что
к свободной поверхности. Учитывая, что 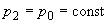 ,
,
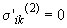 ,
в длинноволновом приближении для стационарного двумерного
решения условие
(3) имеет вид:
,
в длинноволновом приближении для стационарного двумерного
решения условие
(3) имеет вид:
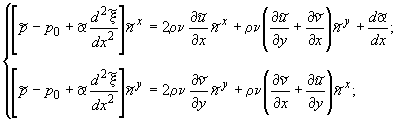 (4)
(4)
где 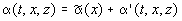 ,
,
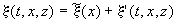 ,
,
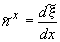 ,
,
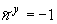 - проекции вектора нормали
- проекции вектора нормали 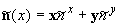 к поверхности
к поверхности 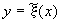 .
При y=0:
.
При y=0:
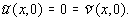 (5)
(5)
Решением задачи (2), (4), (5) является:
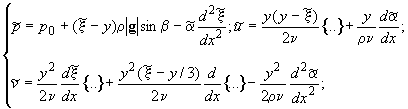 (6)
(6)
здесь 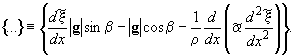 Условие (1) позволяет установить связь между
Условие (1) позволяет установить связь между 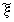 и
и 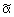 ,
а тем самым – найти искомую зависимость
,
а тем самым – найти искомую зависимость 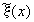 в параметрической форме:
в параметрической форме:
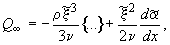 (7)
(7)
постоянная 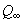 определяется через параметры течения при условии
определяется через параметры течения при условии 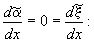
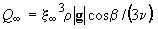 В безразмерной форме (7) имеет вид:
В безразмерной форме (7) имеет вид:
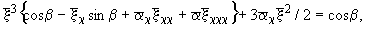 (8)
(8)
где 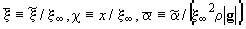 при
при 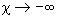
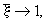 индексы “
индексы “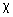 ”
означают дифференцирование по
”
означают дифференцирование по 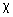 .
В случае малости относительного отклонения
.
В случае малости относительного отклонения 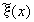 от значения
от значения 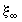 (
(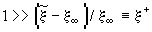 )
получим
из (8) для
)
получим
из (8) для 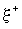 ,
пренебрегая зависимостью давления от поверхностного натяжения:
,
пренебрегая зависимостью давления от поверхностного натяжения:
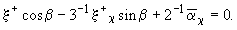 Отсюда видно, что при
Отсюда видно, что при 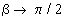
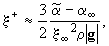 (9)
(9)
а при 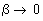 :
:
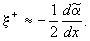 (10)
(10)
В случае (9) форма поверхности представляет
собой “ступеньку”, а в случае (10) - колоколообразное возвышение
с максимумом в точке наибольшего (по модулю) градиента поверхностного
натяжения (и соответственно - температуры поверхности жидкости).
При промежуточных углах наклона 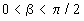 должно реализовываться решение, несущее характерные признаки
решений, полученных для предельных случаев (9, 10), т.е. следует
ожидать, что решение будет иметь вид ступеньки с нарушением
монотонности на фронте.
должно реализовываться решение, несущее характерные признаки
решений, полученных для предельных случаев (9, 10), т.е. следует
ожидать, что решение будет иметь вид ступеньки с нарушением
монотонности на фронте.
Нестационарная задача.
Следующим этапом решения
общей задачи является исследование полученного стационарного
решения (6), (8) на устойчивость по отношению к линейным нестационарным
периодическим по z
возмущениям 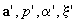 при учете граничных условий (3) на возмущенной свободной поверхности,
условий (5), условия затухания возмущений при
при учете граничных условий (3) на возмущенной свободной поверхности,
условий (5), условия затухания возмущений при 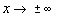 и кинематического условия на возмущенной свободной поверхности:
и кинематического условия на возмущенной свободной поверхности:
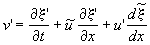 .
Последнее условие в нестационарном случае заменяет условие
постоянства расхода жидкости (в стационарном случае они совпадают).
Решение при
.
Последнее условие в нестационарном случае заменяет условие
постоянства расхода жидкости (в стационарном случае они совпадают).
Решение при 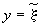 имеет вид:
имеет вид: 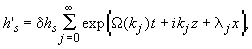 где
где 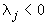 при
при 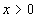 .
В случае
.
В случае 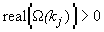 возмущения с периодом
возмущения с периодом 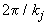 нарастают, а максимум функции
нарастают, а максимум функции 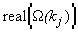 определяет характерный период формирующейся слабонелинейной
структуры.
определяет характерный период формирующейся слабонелинейной
структуры.
Ëèòåðàòóðà.
- Kabov O.A., Marchuk I.V., Chupin V.M. Russian Journal of Engineering Thermophysics, 1996, 6, 2, P. 105-138.
- Ìèíàåâ Ñ.Ñ., Ïèðîãîâ Å.À., Øàðûïîâ Î.Â. // Ôèçèêà ãîðåíèÿ è âçðûâà, 1996, 32, 5, Ñ. 8-16.
- Borissov A.A., Sharypov O.V. // Journal of Fluid Mechanics, 1993, 257, P. 451.
-
ÁîðèñîâÀ.À., Êðàâ÷åíêîÀ.Ã., ØàðûïîâÎ.Â.//Äîêëàäû ÐÀÍ, 1992,324,4,ñ.777
- Íàêîðÿêîâ Â.Å., Ïîêóñàåâ Á.Ã., Øðåéáåð È.Ð. Ðàñïðîñòðàíåíèå âîëí â ãàçî- è ïàðîæèäêîñòíûõ ñðåäàõ. – Íîâ-ñê: Èíñòèòóò òåïëîôèçèêè ÑÎ ÐÀÍ, 1983.
- Ãåðøóíè Ã.Ç., Æóõîâèöêèé Å.Ì. Êîíâåêòèâíàÿ óñòîé÷èâîñòü íåñæèìàåìîé æèäêîñòè. - Ì.: Íàóêà, 1972.
- Øëèõòèíã Ã. Òåîðèÿ ïîãðàíè÷íîãî ñëîÿ. – Ì.: Íàóêà, 1969.
Ëàíäàó Ë.Ä., Ëèôøèö Å.Ì. Ãèäðîäèíàìèêà. – Ì.: Íàóêà, 1986.

