САМОВОЗДЕЙСТВИЕ ИЗЛУЧЕНИЯ И УСТАНАВЛИВАЮЩИЕСЯ СОСТОЯНИЯ СИСТЕМ, ОПИСЫВАЕМЫХ УРАВНЕНИЕМ ГИНЗБУРГА-ЛАНДАУ
А.К. Комаров
Институт автоматики и электрометрии СО PАН
Уравнение Гинзбурга-Ландау широко используется при описании различного типа нелинейных систем и явлений: пассивная синхронизация лазерных мод, распространение ультракоротких импульсов в волоконных линиях связи, сверхпроводимость, гидродинамические неустойчивости, бозе-конденсация и т.д. [1,2,3]. Настоящая работа продолжает наши исследования (в рамках данного уравнения) переходного процесса и устанавливающихся режимов генерации, возникающих при фазомодуляционной неустойчивости пассивной синхронизации лазерных мод [4,5,6].
В модели распределенной внутрирезонаторной среды в системе координат движущегося импульса, уравнение, описывающие эволюцию внутрирезонаторного излучения в безразмерных переменных, имеет вид [6]
|
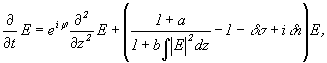
|
(1) |
где E(z, t) – амплитуда поля; t – временнáя переменная; z – координата; параметр j
определяет отношение частотной дисперсии показателя преломления к дисперсии усиления q
= tg j
. Первое слагаемое в круглых скобках описывает насыщающееся усиление. Второе слагаемое связано с линейными резонаторными потерями. Слагаемое d
s
описывает нелинейные потери. Последнее слагаемое определяет фазовую модуляцию формируемого импульса, вызванную нелинейным показателем преломления d
n. Переходный процесс и устанавливающиеся режимы генерации исследовались при различных параметрах дисперсии и типах нелинейности.
1. d
s
= – q¢
½
E½
2, d
n = q¢
¢
½
E½
2. При таком типе нелинейностей уравнение (1) имеет решение в виде стационарного импульса Es(z) = Eo exp(id
w
t)sech1+ia
(b
z). Пиковая амплитуда Eo, обратная длина b
, параметр фазовой модуляции a
и изменение несущей частоты светового импульса d
w
определяются из системы алгебраических уравнений, получаемых при подстановке Es(z) в (1). Необходимым условием устойчивости этого импульса является отрицательность полного усиления, включающего потери, вне объема импульса. Из (1) и найденных величин Eo, b
, a
получаем аналитическое выражение для этого условия через параметры дисперсии q
и нелинейности x
= q¢
¢
/q¢
:
|
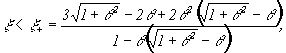
|
(2) |
|
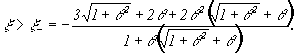
|
(3) |
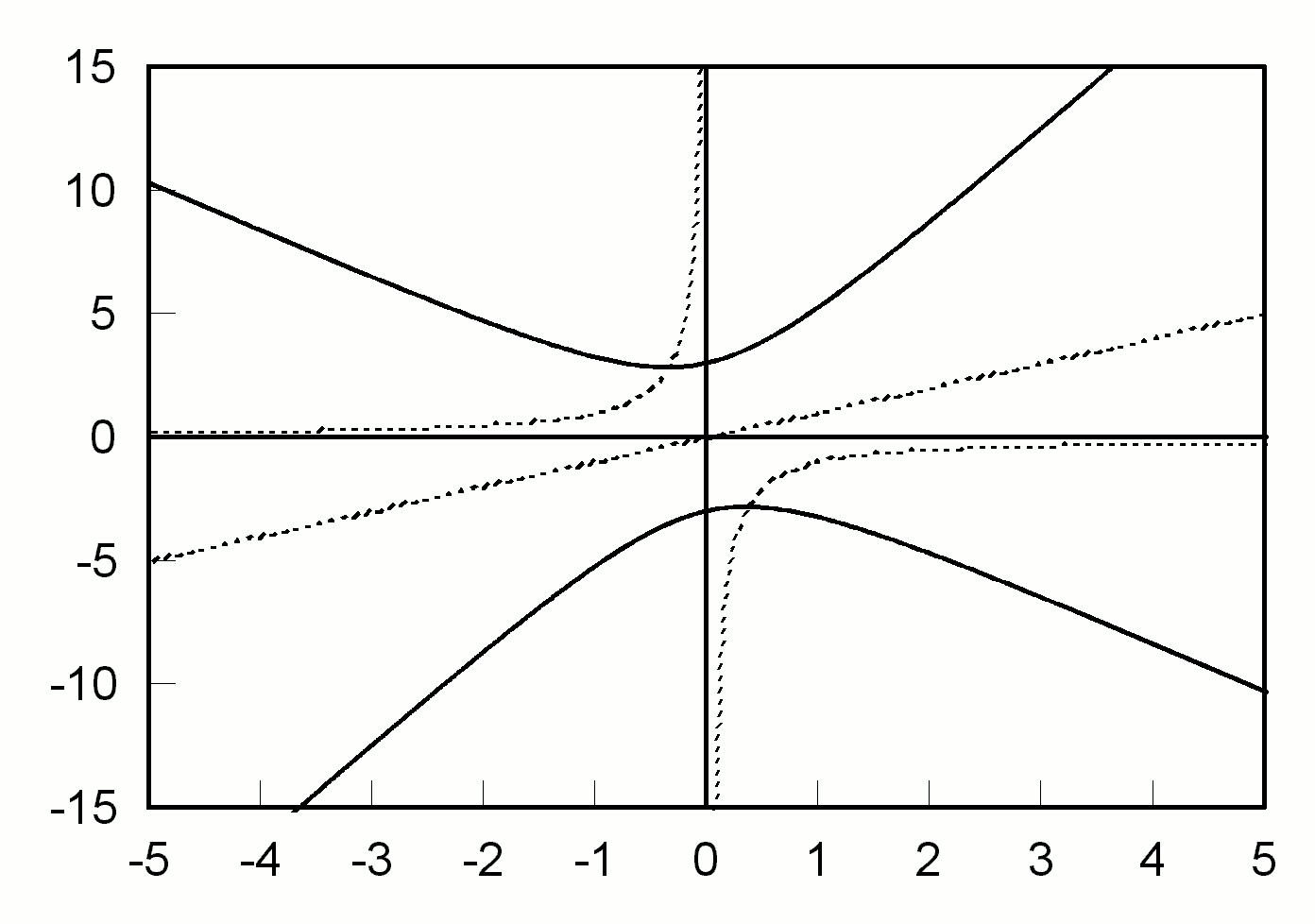
Кривые x
= x
± отмечены на рис. 1 сплошной (на пунктирной прямой a
= 0, на пунктирных кривых ½
a
½
= Ö
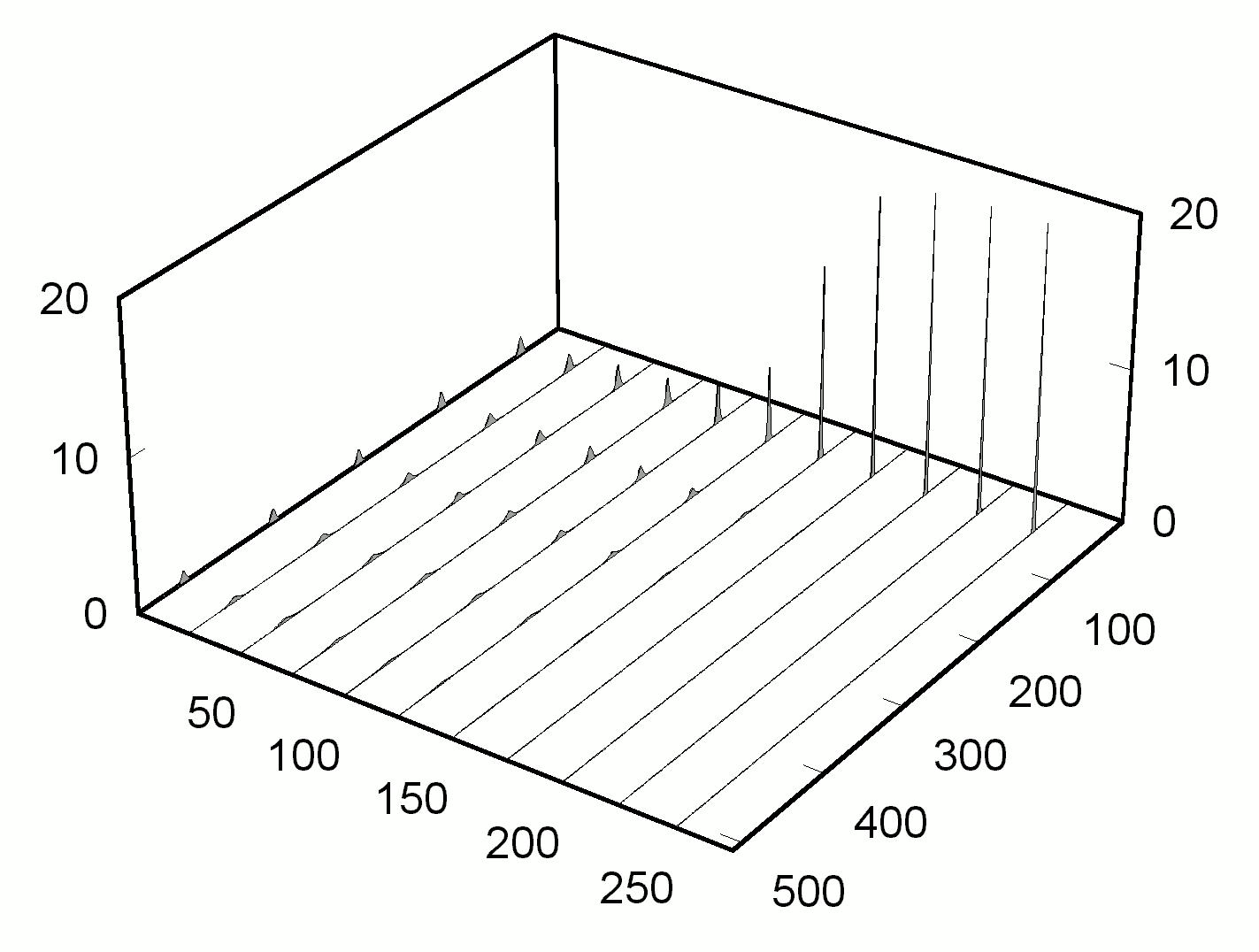
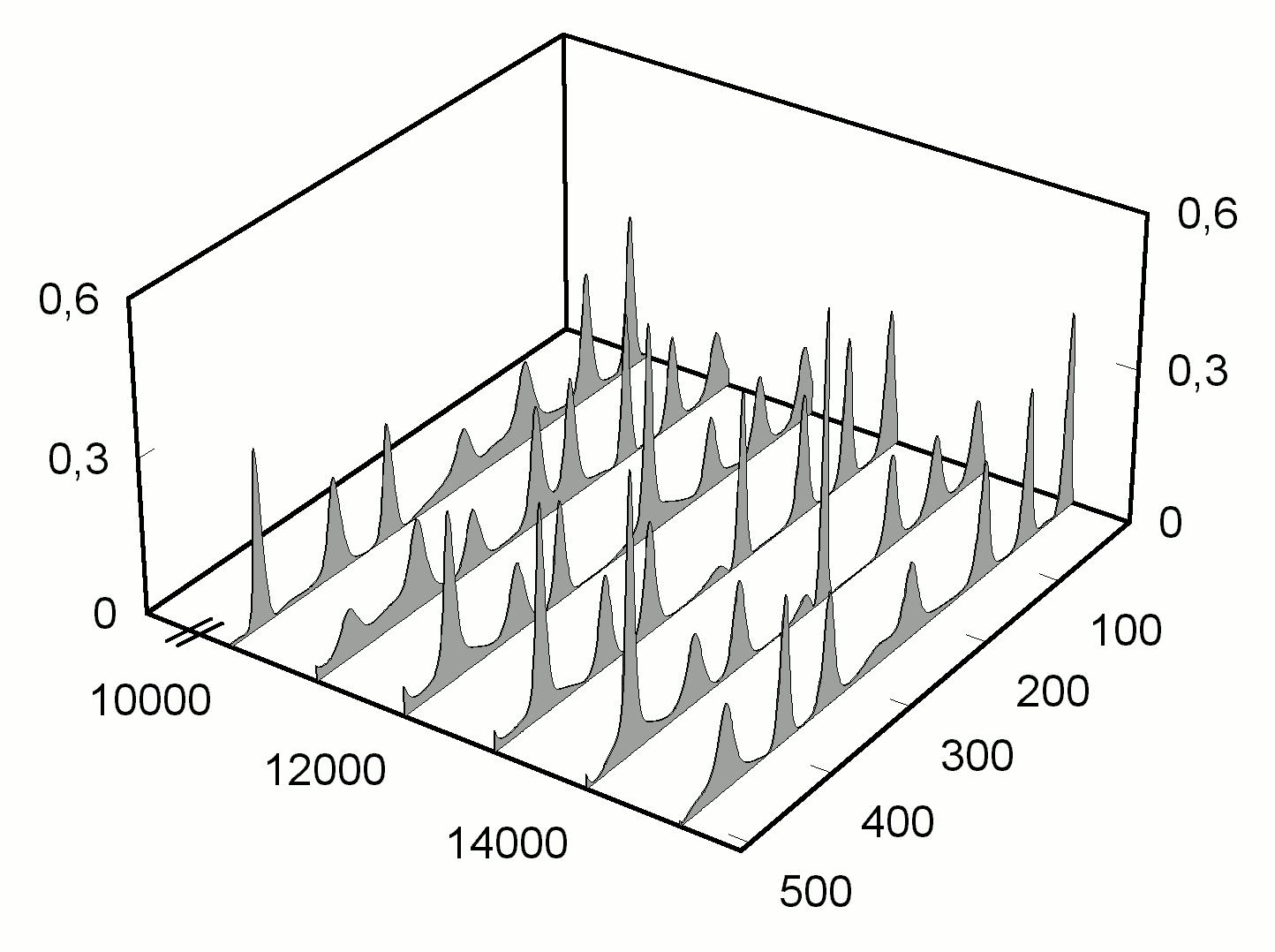
2 ). Как показывает численный счет, область параметров между сплошными кривыми соответствует реализации после переходного процесса режима одиночного стационарного импульса Es(z), а при параметрах лазерной системы вне этой области устанавливается режим генерации с заполнением всего лазерного резонатора хаотически меняющимися импульсами. Примеры таких режимов приведены на рис. 2.
|
|
|
Рис. 1. Области параметров частотной дисперсии и нелинейности (1), при которых устанавливаются режим одиночного стационарного импульса и режим с заполнением всего лазерного резонатора нестационарными импульсами. |
|
|
|
|
Рис. 2. Режимы генерации, характерные для двух областей параметров x
, q
, представленных на рис. 1. a = 3, b = 0.1, j
= 1. a — q¢
= 0.05, q¢
¢
= 0.29; b — q¢
= 0.02, q¢
¢
= 0.30. |
d
s
= – q¢
½
E½
2/(1 + ½
E½
2), d
n = q¢
¢
½
E½
2. Этот случай отличается от предыдущего тем, что эффективная нелинейность потерь зависит от интенсивности излучения и падает с ростом интенсивности (q¢
ef = q¢
½
E½
2/(1+½
E½
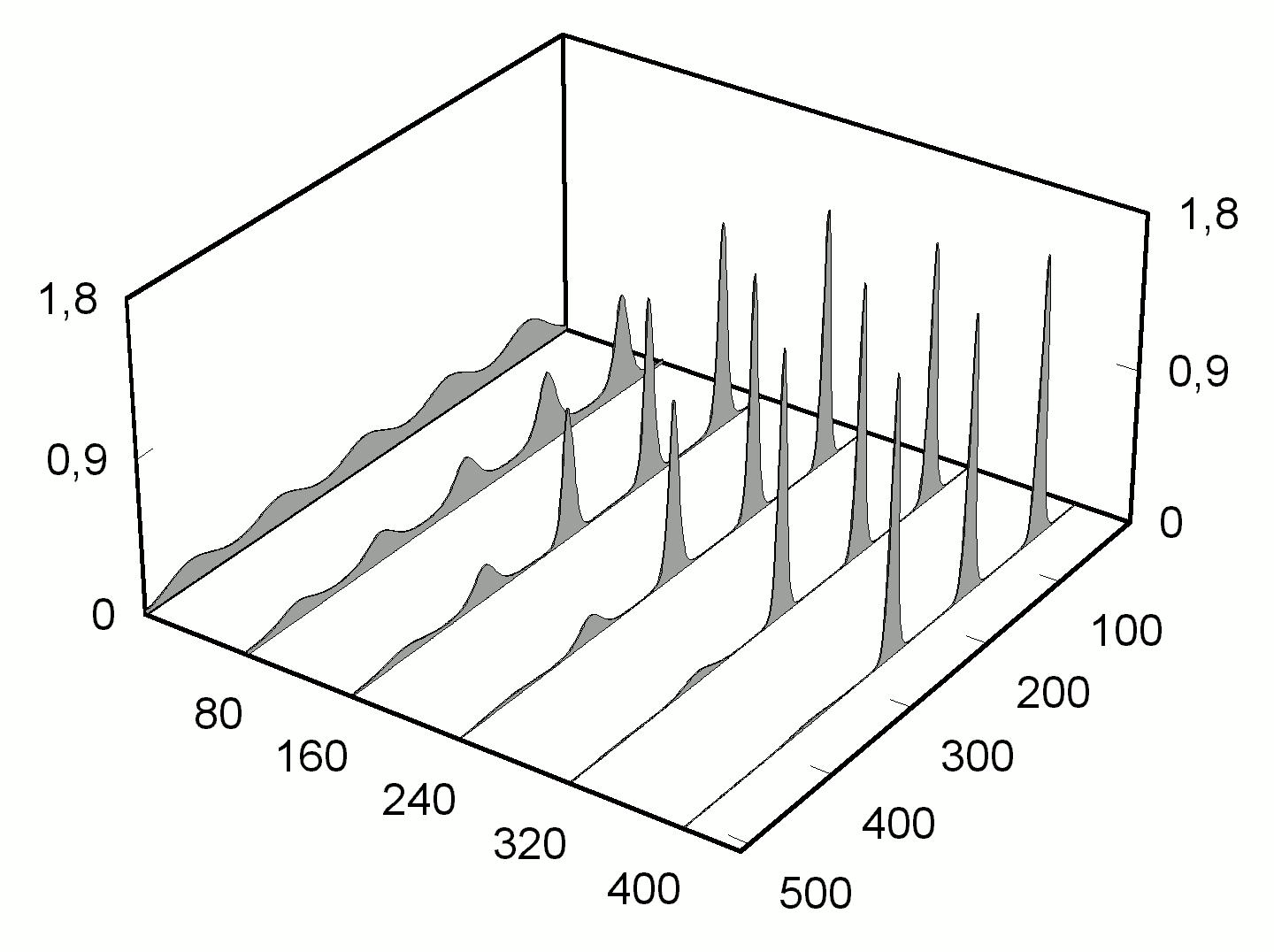
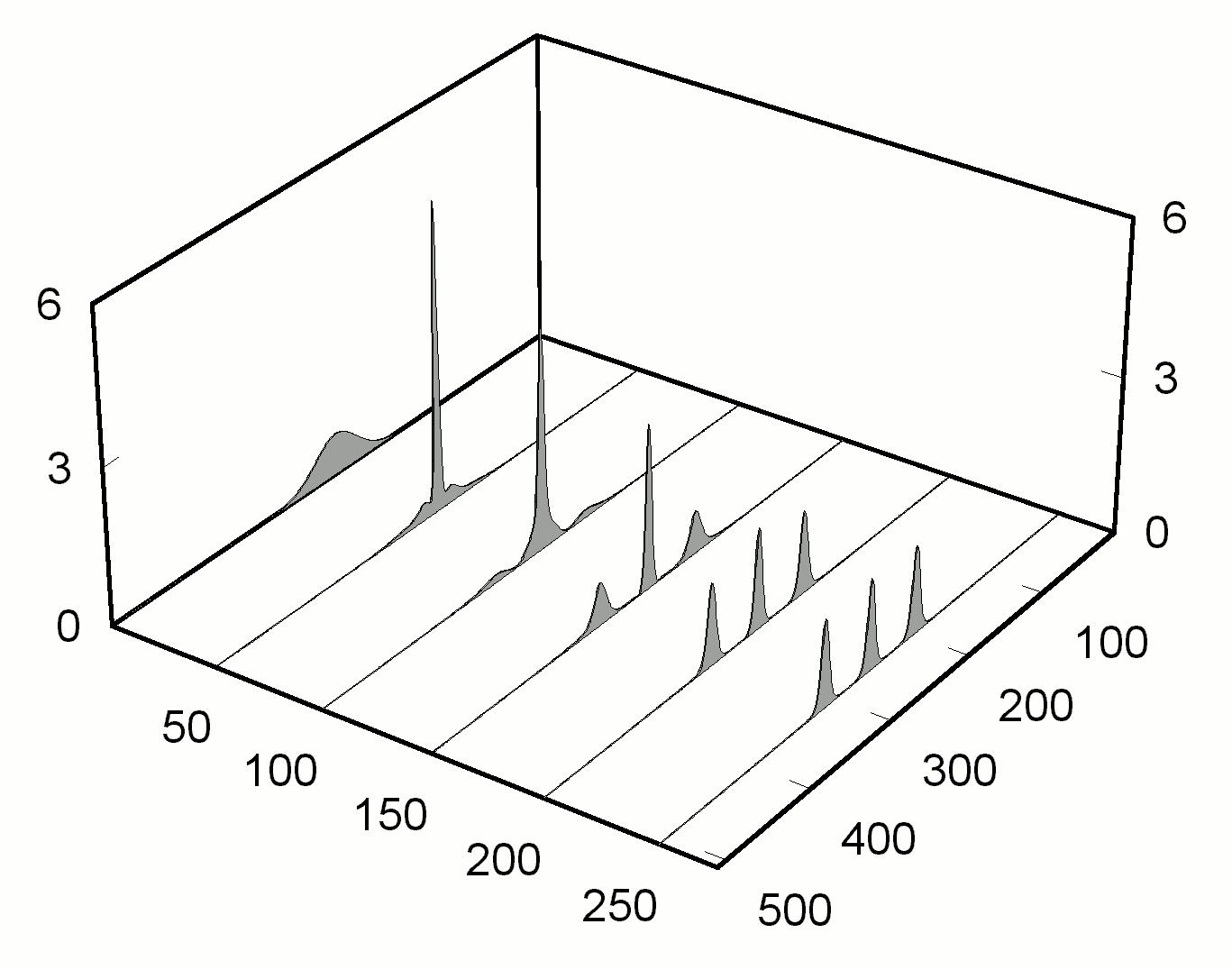
2). При таком типе нелинейности возникает область параметров, при которых реализуется новый устанавливающийся режим генерации — режим нескольких одинаковых стационарных импульсов. Число импульсов зависит от накачки и величин нелинейностей показателя преломления и потерь. Пример реализации такого режима при разных начальных условиях приведен на рис. 3.
|
|
|
|
Рис. 3. Переходная эволюция и устанавливающийся режим генерации нескольких стационарных импульсов при насыщающихся нелинейных потерях (2) и различных начальных условиях. a = 3, b = 0.1, j
= 1, q¢
= 0.11, q¢
¢
= 0.28. |
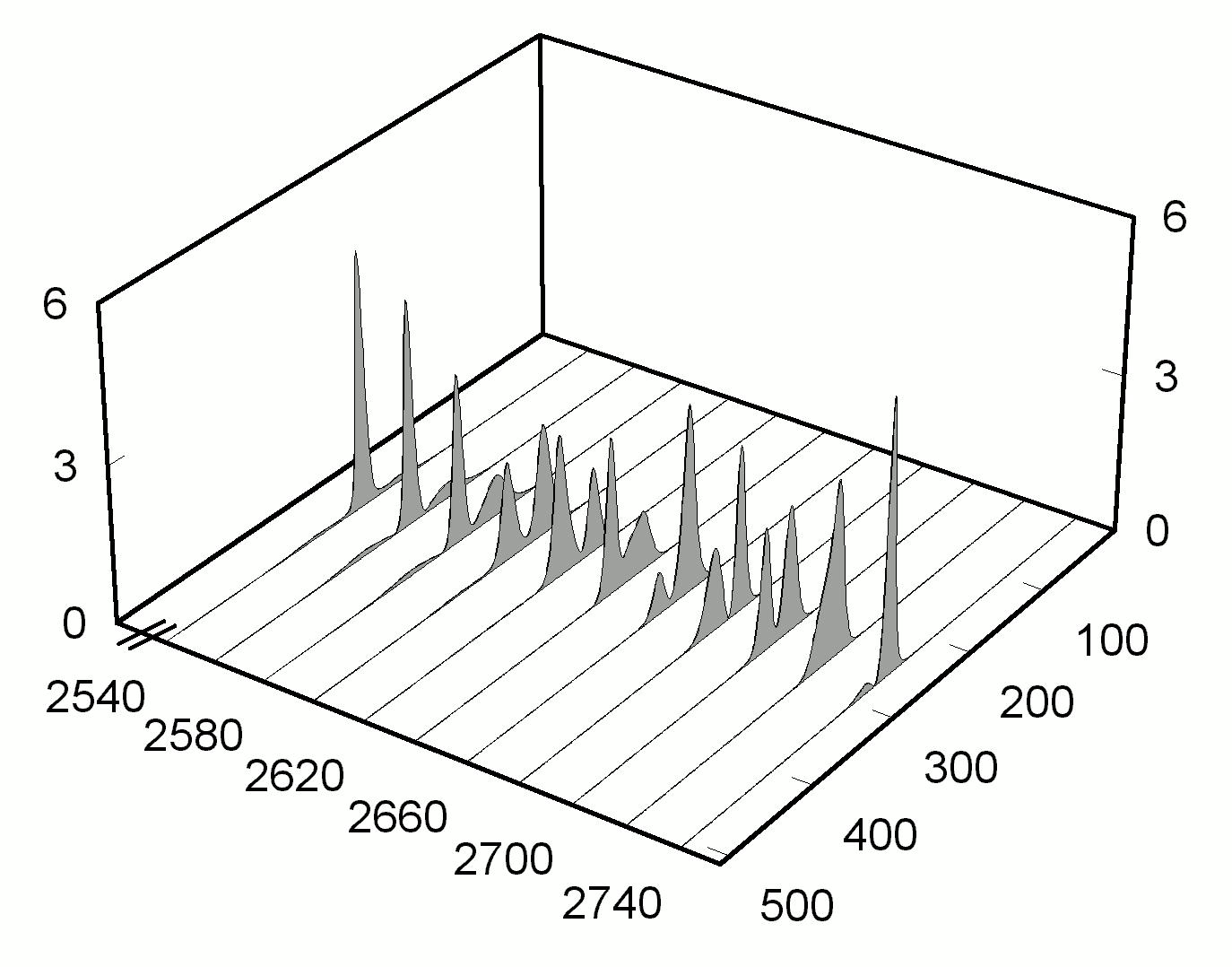
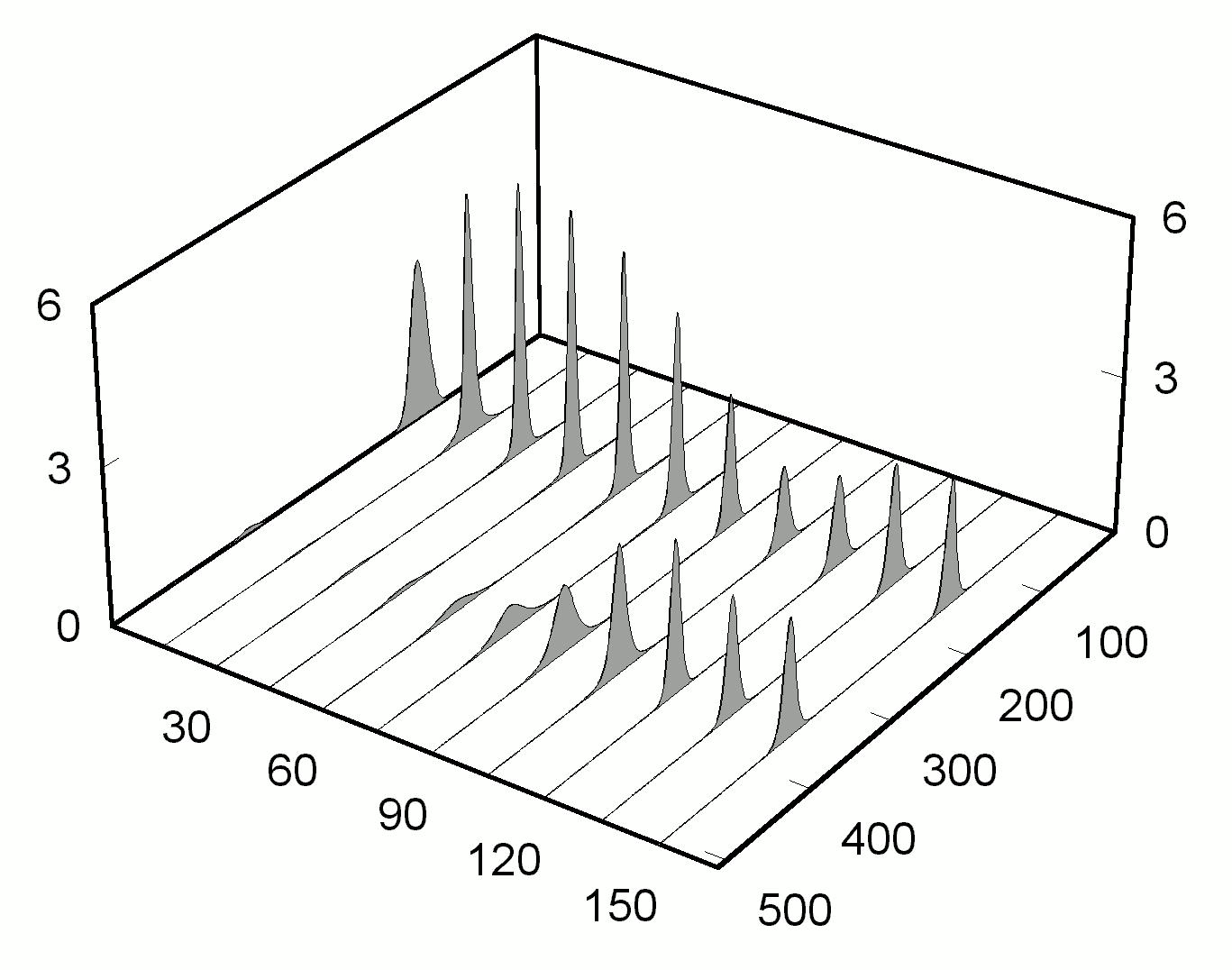
Другой особенностью генерации при рассматриваемых типах нелинейности является возникновение бистабильности. На основе численного счета обнаружено, что в зависимости от начальных условий может реализоваться либо режим двух стационарных импульсов, либо режим с периодическим распадом импульса на два импульса и последующим их слиянием в одиночный импульс. При этом происходит случайная вариация периода этого процесса и пространственной структуры излучения. Пример реализации такого типа зависимости устанавливающегося режима генерации от начальных условий приведен на рис. 4.
|
|
|
|
Рис. 4. Зависимость устанавливающегося режима при нелинейностях (2) от начальных условий генерации. a = 3, b = 0.1, j
= 0, q¢
= 0.30, q¢
¢
= 0.24. |
d
s
= – q¢
½
E½
2, d
n = q¢
¢
½
E½
2/(1 + k
½
E½
2). В этом случае эффективная нелинейность показателя преломления зависит от интенсивности (q¢
¢
ef = q¢
¢
/(1 + k
½
E½
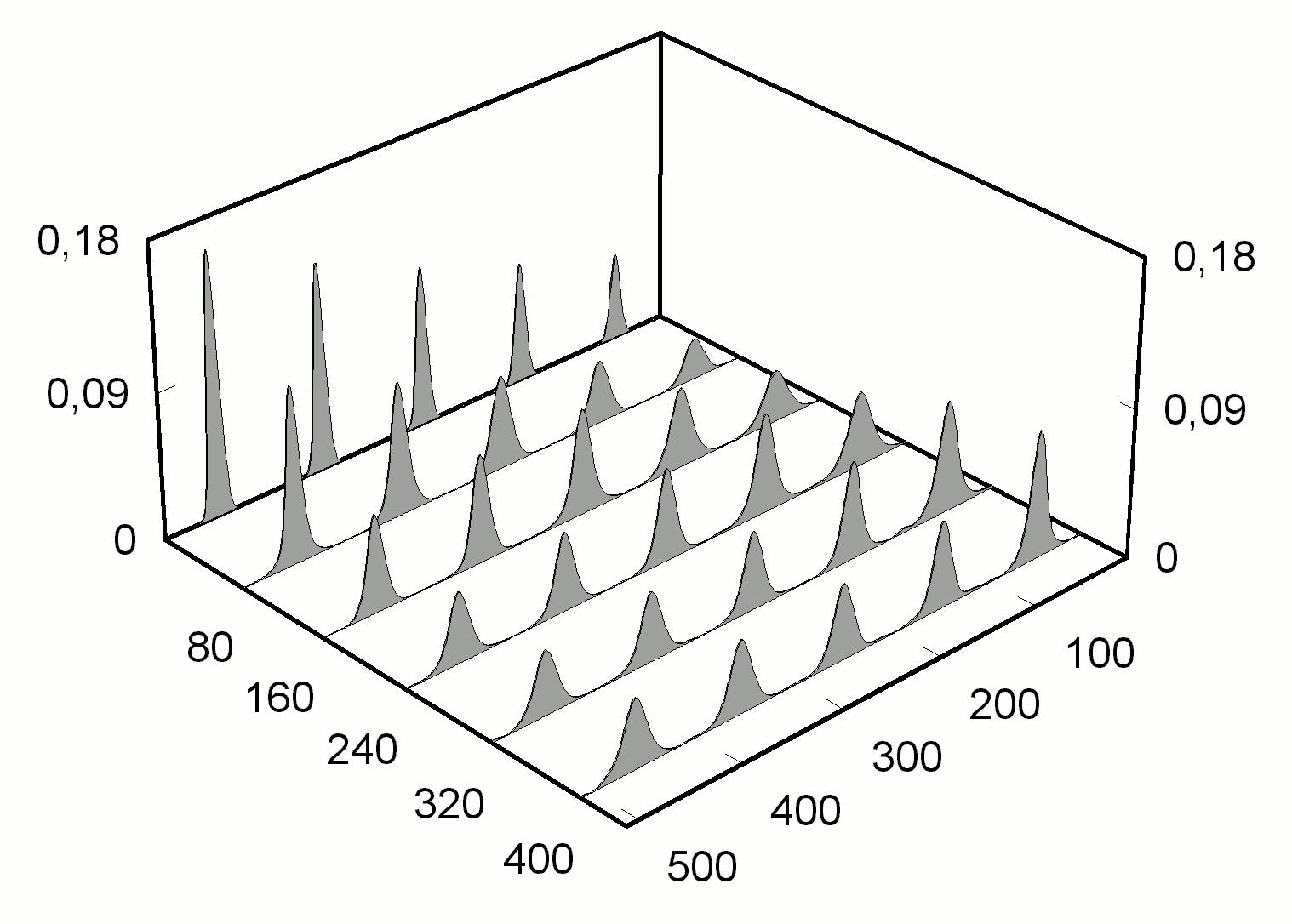
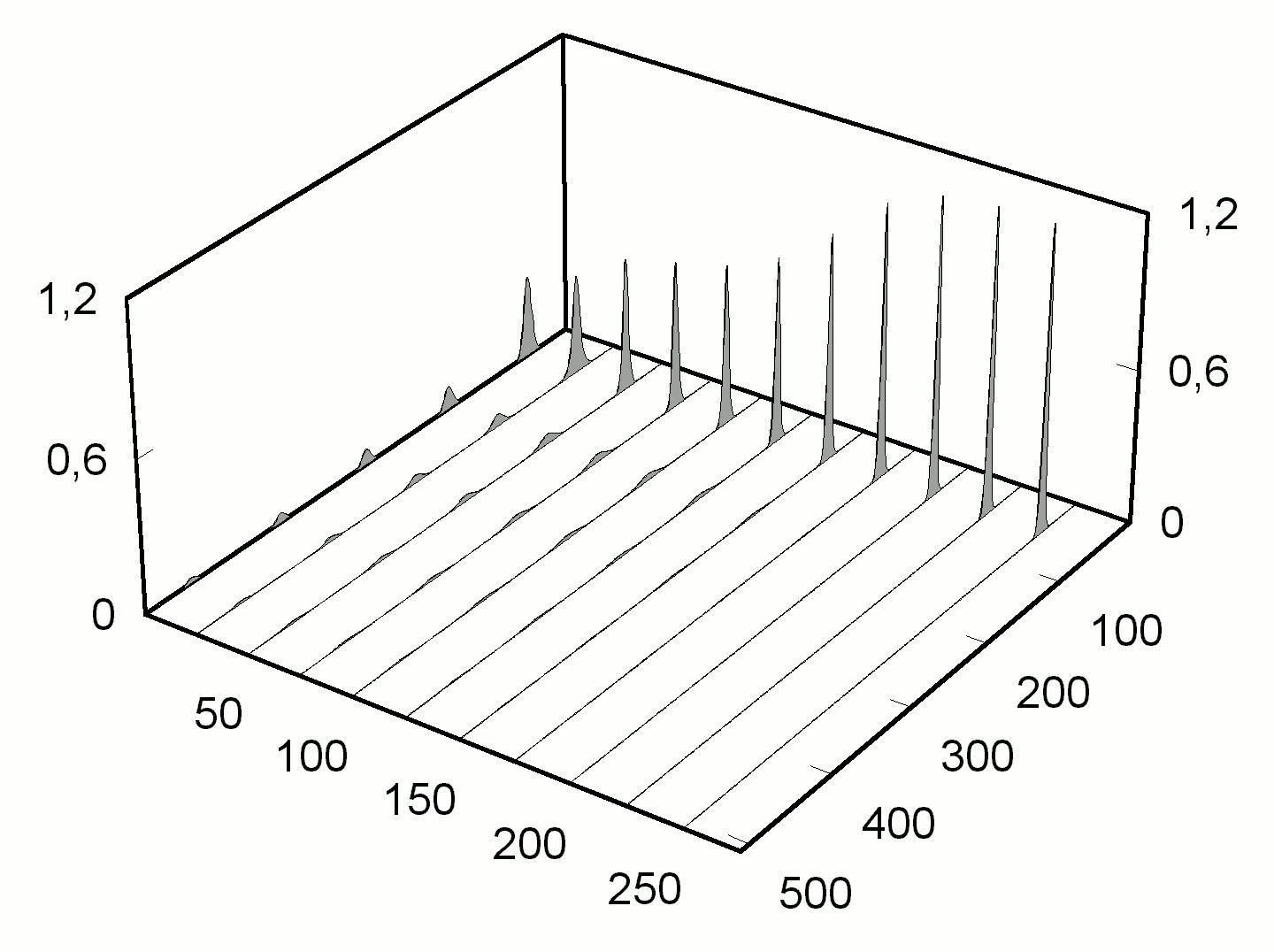
2). При такого вида нелинейностях в широкой области параметров системы возникает еще один тип бистабильности. В зависимости от начальных условий генерации реализуется либо режим одиночного стационарного импульса, либо режим с заполнением всего лазерного резонатора хаотически меняющимся излучением. Рис. 5 демонстрирует такого типа зависимость устанавливающего режима генерации от начальных условий переходного процесса.
|
|
|
|
Рис. 5. Бистабильность пассивной синхронизации лазерных мод при насыщающейся нелинейности показателя преломления (3). a = 2, b = 0.3, j
= – 0.5, k
= 1, q¢
= 0.30, q¢
¢
= 1.50. |
Итак, устанавливающимся режимом пассивной синхронизации лазерных мод, описываемой уравнением Гинзбурга-Ландау с насыщающимся усилением, в зависимости от соотношений между дисперсиями усиления и показателя преломления и нелинейностями потерь и показателя преломления является либо режим одиночного стационарного импульса, либо режим генерации с заполнением всего лазерного резонатора хаотически меняющимся излучением.
Если нелинейность потерь зависит от интенсивности и уменьшается с ростом интенсивности, то при определенных параметрах системы может реализоваться новый режим генерации — режим нескольких одинаковых стационарных импульсов. Количество импульсов зависит от параметров системы. Обнаружено, что такая система обладает свойством бистабильности. В зависимости от начальных условий может реализоваться либо режим двух стационарных импульсов, либо режим одиночного импульса с периодически меняющейся формой и амплитудой.
Обнаружено, что, если нелинейность показателя преломления уменьшается с ростом интенсивности, то возможен другой тип бистабильности. В зависимости от начальных условий реализуется либо режим одиночного стационарного импульса, либо происходит заполнение всего резонатора хаотически меняющимся излучением. Аналогичный тип бистабильности возникает также при нелинейном показателе преломления с конечным временем релаксации.
Полученные результаты носят достаточно общий характер и могут представлять интерес для специалистов, занимающихся изучением других нелинейных систем, описываемых уравнением Гинзбурга-Ландау.
Представленная работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 98–02–17791) и Международной Соросовской программы образования в области точных наук (грант № s99–400).
Литература
- S. Popp, O. Stiller, E. Kuznetsov, L. Kramer, Physica D, 114, 81 (1998).
- L. Kramer, E.A. Kuznetsov, S. Popp, S.K. Tutitsyn, Pis'ma v Zhetf, 61, 887 1995
- E. Kaplan, E. Kuznetsov, V. Steinberg, Phys. Rev. E, 50, 3712 (1994).
- А.К. Комаров, А.С. Кучьянов, А.М. Мищенко, Автометрия, № 4, 378 (1999).
- A.K. Komarov, K.P. Komarov, A.S. Kuch'yanov, In: Fundamental Problems of Laser Optics, Proceedings of SPIE, 3685, 28, 1999.
А.К. Комаров, К.П. Комаров, А.С. Кучьянов, Письма в ЖЭТФ 67, 261 1998.

