РАСПРОСТРАНЕНИЕ КОРОТКИХ ИМПУЛЬСОВ В РЕЗОНАНСНОЙ ТРЕХУРОВНЕВОЙ СРЕДЕ В УСЛОВИЯХ АДИАБАТИЧЕСКОГО ПЕРЕНОСА НАСЕЛЕННОСТИ

В.Г. Архипкин, И.В. Тимофеев

Институт физики им. Л.В. Киренского СО РАН, Красноярский государственный университет

В работе исследуются особенности пространственно-временной эволюции двух частично перекрывающихся коротких импульсов контр-интуитивной последовательности в среде трехуровневых поглощающих атомов в условиях адиабатического переноса населенности. Построено аналитическое решение и показано, что эффект селективного возбуждения двухфотонно резонансного состояния с вероятностью, практически близкой к единице, сохраняется на длине, которая на несколько порядков может превышать длину линейного поглощения слабого пробного импульса в отсутствие управляющего излучения на смежном переходе.

1. В последнее время огромный интерес привлекают исследования резонансного взаимодействия двух лазерных импульсов (пробного и управляющего) с трехуровневыми атомами 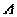-конфигурации. Некоторые аспекты распространения лазерных импульсов в условиях электромагнитно индуцированной прозрачности исследовались, например, в [1-6]. Как правило, рассматривались ситуации, когда оба импульса имеют одинаковую форму, а их длительность больше времени релаксации промежуточного резонансного состояния (согласованные импульсы [1]; импульсы, одетые полем [2,3]) или длительность управляющего излучения значительно превышает длительность пробного (адиабатоны [5,6]).

Достаточно хорошо изучена временная эволюция адиабатического переноса населенности (АПН) [7-11], но, насколько нам известно, не исследован вопрос о пространственной эволюции самих взаимодействующих импульсов в оптически плотной среде и о пространственной динамике населенности конечного состояния, возбуждаемого в процессе взаимодействия. В данной работе приводятся результаты исследования пространственно-временной эволюции двух одинаковых частично перекрывающихся коротких импульсов контр-интуитивной последовательности (управляющий импульс включается и выключается раньше, чем пробный [10]) в поглощающей трехуровневой среде в условиях АПН. Эффект АПН наблюдается для импульсов, огибающие которых изменяются достаточно медленно и удовлетворяют критерию адиабатичности [10]:

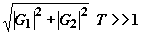(1)

где 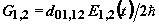, 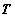¾ частота Раби и длительность взаимодействующих импульсов, соответственно. Это условие адиабатичности может быть выполнено и для коротких, но достаточно мощных импульсов контр-интуитивной последовательности, длительность которых существенно меньше всех времен релаксации атомной подсистемы [3,10]. Именно такую ситуацию далее мы будем рассматривать. Теоретическая модель состоит из системы связанных уравнений Шредингера и укороченных волновых уравнений для частот Раби, самосогласованно описывающих временную и пространственную динамику атомной подсистемы и излучения. В адиабатическом приближении (1) построено аналитическое решение и предлагается трехмерная векторная модель адиабатического следования. Показано, что пробный импульс может распространяться на расстояние, значительно превышающее длину линейного поглощения, но, в конечном счете, он полностью перекачивается в управляющий импульс. При этом АПН приводит практически к полной инверсии населенности на дипольно-запрещенном переходе на конечной характерной длине распространения пробного импульса, когда амплитуды частот Раби изменяются не очень сильно.

2. Рассмотрим распространение двух частично перекрывающихся импульсов в среде трехуровневых атомов, показанных на рис.1. Промежуточное состояние 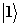однофотонно резонансно каждому из полей, которые взаимодействуют только со "своим" переходом. Далее будем называть импульс с частотой 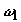пробным, а другой -- управляющим. Импульсы следуют в определенной временной последовательности: сначала атомы взаимодействуют с управляющим импульсом 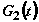на переходе 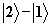, а затем с пробным импульсом 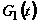, который включается несколько позже – на переходе 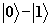(рис.1). Импульсы распространяются колинеарно вдоль направления 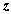, одинаково линейно поляризованы и имеют одинаковую (гауссовскую) форму и длительность.

Рис.1. Конфигурация энергетических уровней в атоме и огибающие частот Раби импульсов на входе в среду. ¾ несущие частоты пробного и управляющего импульсов, соответственно.

Система уравнений для амплитуд вероятностей 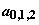и частот Раби взаимодействующих импульсов 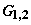в движущейся системе координат с локальным временем 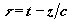имеет вид:

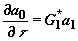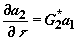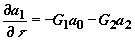, , , (2)

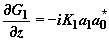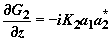, . (3)

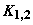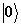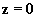¾ постоянная распространения. Считаем, что все атомы в момент включения полей находятся в основном состоянии , а на входе в среду оба импульса имеют гауссовскую огибающую 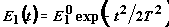, , 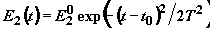где 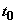¾ время задержки между импульсами, 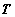¾ длительность импульса.

В адиабатическом приближении решение системы (2) можно представить в виде:

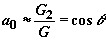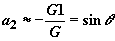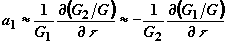, , , (4)

где 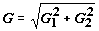, 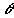¾ некоторый угол, смысл которого будет расшифрован ниже.

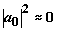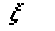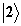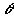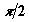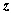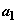Из (4) следует, что в конце управляющего импульса , , т.е. населенность основного состояния переносится в состояние . При этом угол изменяется от нуля до . В действительности величина этого угла зависит еще и от координаты, как будет показано ниже, поэтому это справедливо только до определенных значений . Выражение для можно привести к виду: 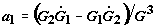. Нетрудно показать, что в приближении (1) величина 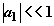, т.е. населенность промежуточного состояния 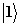практически отсутствует в течение всего времени взаимодействия с импульсами. Последнее физически означает, что резонансное поглощение импульсов мало - индуцированная прозрачность. Поэтому импульсы могут распространяться на расстояние, существенно превышающее длину линейного поглощения слабого пробного излучения в отсутствии управляющего.

Подставляя решение (4) в полевые уравнения (3), получаем систему связанных нелинейных уравнений

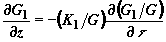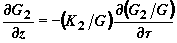, . (5)

Из (5) нетрудно показать, что сумма 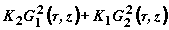не зависит от координаты 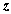и равна . Это отражает тот факт, что импульсы распространяются согласованно. Поэтому данную суперпозицию импульсов (по аналогии с [2]) можно идентифицировать как импульсы, одетые полем. Но в нашем случае, в отличие от [2], длительность импульсов много меньше всех времен релаксации атомной подсистемы. Отметим,что интеграл .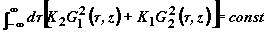

В общем случае решение системы (5) не удается записать в квадратурах. Но при 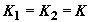оно находится, например, методом характеристик, и его можно представить в виде:

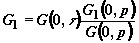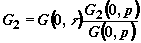, . (6)

Здесь 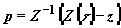, , 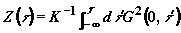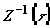¾ обратная функция .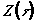

На рис.2 показаны зависимости нормированных частот Раби 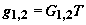от времени и глубины проникновения излучения в среду, вычисленные по формуле (6). Они демонстрируют, что в резонансной среде пробный импульс может распространяться на расстояние, которое на несколько порядков превышает длину линейного поглощения. При этом энергия переднего фронта пробного импульса частично поглощается, а энергия заднего фронта управляющего ¾ увеличивается. Поглощенная энергия затрачивается на адиабатический перевод атомов в возбужденное конечное состояние и на усиление управляющего импульса. По мере распространения амплитуда пробного импульса медленно уменьшается, а управляющий импульс изменяет свою форму и становится "двугорбым". В конечном счете, пробный импульс полностью перекачивается в управляющий импульс, приводя к увеличению площади последнего.

а)	б)
Рис.2. Зависимости нормированных огибающих частот Раби (а) и (б) от времени и глубины проникновения излучений в среду при следующих значениях параметров: , , ( ¾ значения частот Раби в максимуме); , , . Время измеряется в единицах длительности импульса , а длина распространения импульсов в среде в единицах длины линейного поглощения пробного излучения с частотой .

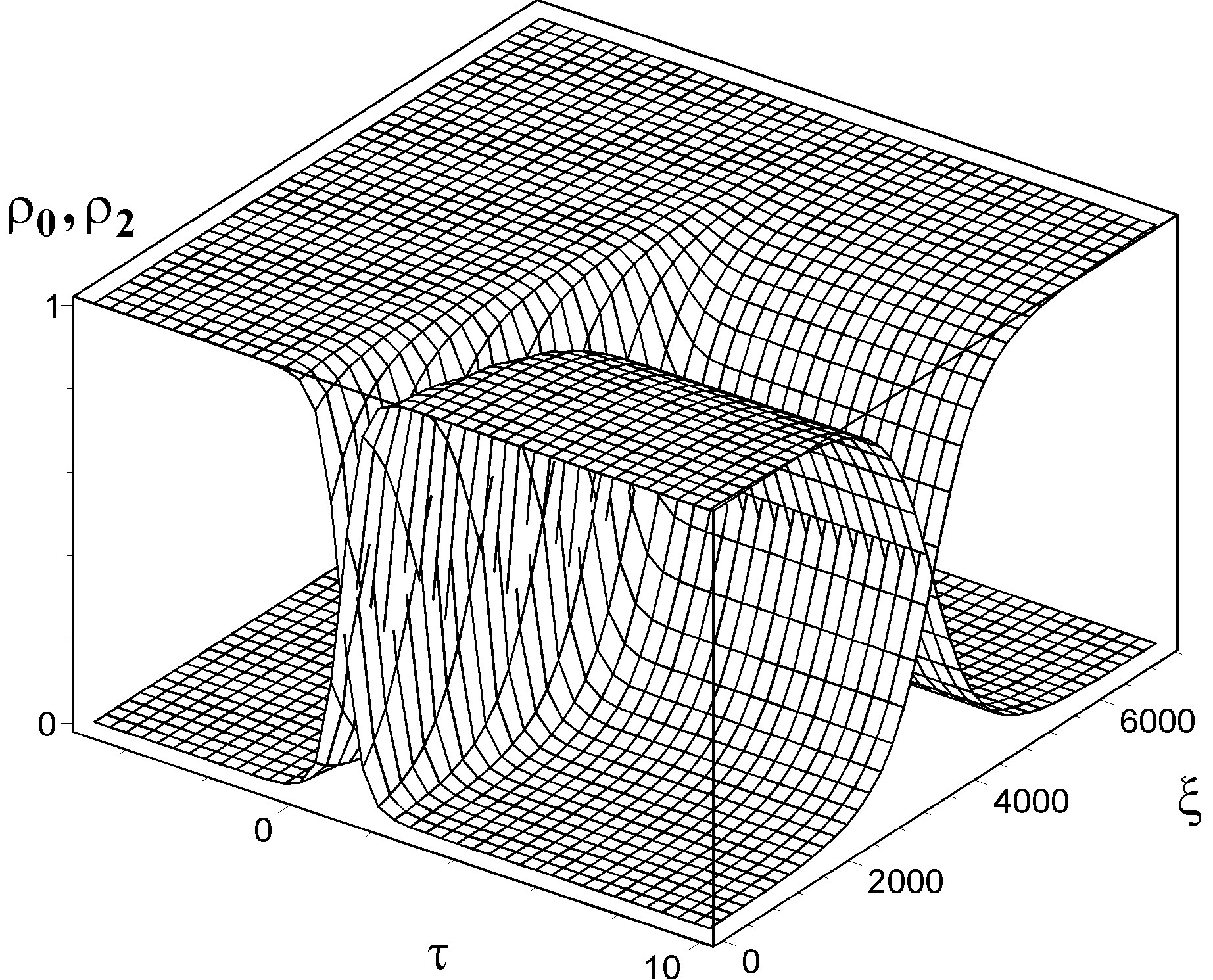
На рис.3 показаны зависимости населенностей 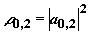от времени и длины среды. Таким образом, перенос населенности имеет место только на определенной длине среды. Чем больше интенсивности взаимодействующих импульсов, тем больше эта длина. Полученные аналитические результаты совпадают с результатами численного анализа системы уравнений (2) и (3) [12].

3. Эти результаты можно интерпретировать на "языке" трехмерной векторной модели, используя в качестве переменных вектора 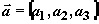и 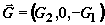(рис. 4). В указанных обозначениях система (2) принимает вид:

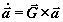, (7)

где знак 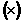означает векторное произведение.

Рис.3. Зависимости населенностей уровней 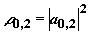от времени и глубины проникновения излучений в среду. Значения параметров такие же как на рис.2.

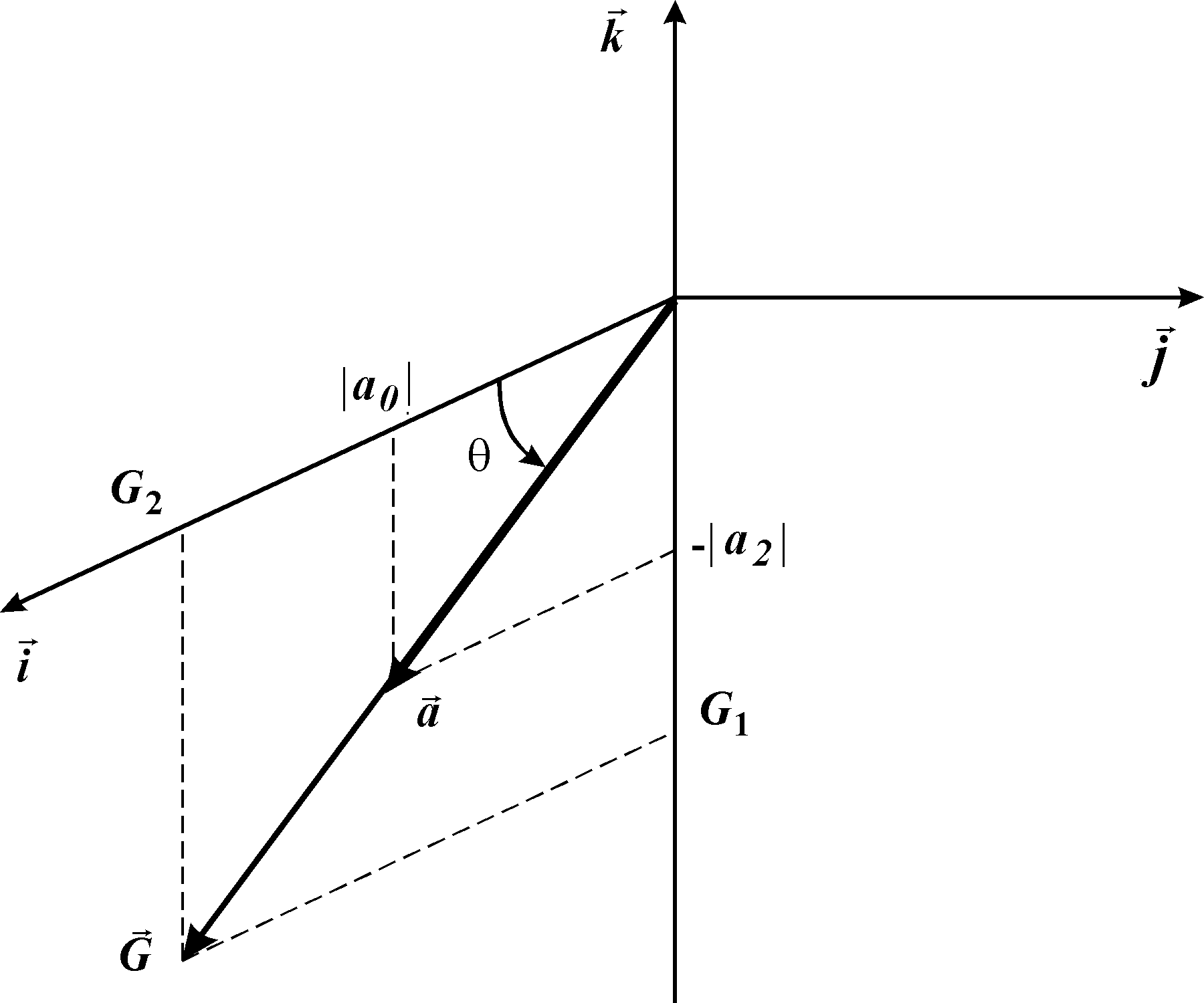
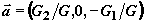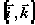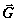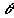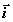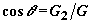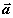Решение уравнения (7) есть вектор , лежащий в плоскости , в которой находится и вектор под углом к оси , где . Компоненты вектора практически совпадают с адиабатическим решением (4), так как 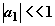и этой величиной можно пренебречь. Поэтому вектор 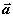, соответствующий адиабатическому решению (4) практически параллелен вектору 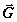и прецессирует вокруг него с частотой 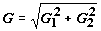, адиабатически следуя за ним. В процессе взаимодействия 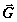поворачивается на 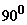, что и означает перенос населенности из основного состояния 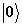в конечное 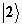. Таким образом, имеется аналогия со случаем адиабатического слежения при взаимодействии импульса света с двухуровневым атомом (см., например, [13]). С учетом распространения угол 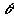является функцией времени и координаты, поэтому описанная выше картина имеет место лишь на длинах, где амплитуды огибающих частот Раби еще не сильно отличаются друг от друга. При больших длинах среды эффект исчезает. Эти выводы не зависят от формы импульсов, если удовлетворяется условие адиабатичности.

4. В данной работе исследован эффект АПН с учетом влияния распространения взаимодействующих контр-интуитивных импульсов в оптически плотной трехуровневой среде с -конфигурацией атомных уровней. Показано, что эффект АПН приводит практически к полной инверсии на дипольно запрещенном переходе в протяженной оптически плотной среде, длина которой на несколько порядков может превышать линейную длину поглощения пробного импульса. Приготовленную таким образом среду можно использовать для преобразования частоты пикосекундных и фемтосекундных лазеров в антистоксово излучение с перестраиваемой длиной волны, а также, по-видимому, для наблюдения кооперативного антистоксова рассеяния света.

Рис.4. Векторная модель адиабатического взаимодействия двух коротких импульсов с трехуровневой -системой.

Работа выполнена при финансовой поддержке научной программы "Университеты России ¾ фундаментальные исследования"

Литература

1. S.E.Harris. Phys.Rev.Lett., 72, 52 (1994).
2. J.H.Eberly, M.L.Pons, H.R.Hag. Phys.Rev.Lett. 72, 56 (1994);
3. J.H.Eberly. Quantum Semiclass. Opt. 7, 373 (1995).
4. N.Wang, H.Rabitz. Phys.Rev.A, 51, 5029 (1995).
5. J.H.Eberly, A.Rahman. Phys.Rev.Lett., 76, 3687 (1996).
6. M.Fleischhauer, A.S.Manka. Phys.Rev.A, 54, 794 (1996).
7. Л.В. Кузьмин, В.Н.Сазонов. ЖЭТФ 79, 1759 (1980).
8. J.Oreg, F.T.Hioe, J.H.Eberly. Phys.Rev.A. 29, 690 (1984).
9. F.T.Hioe. Phys. Letters. 1983, 99A, 150 (1983).
10. J.R.Kuklinski, U.Gaubats, F.T.Hioe, K.Bergman. Phys.Rev. A. 40, 6741 (1989).
11. U.Gaubats, P.Rudecki, K.Bergman. J.Chem Phys. 92 5363 (1990).
12. В.Г.Архипкин, Д.В.Манушкин, В.П.Тимофеев. Квантовая электроника, 25, 1084 (1998).

Л.Аллен, Дж.Эберли. Оптический резонанс и двухуровневые атомы. М.: Мир,1978.