ОБРАТНОЕ РАССЕЯНИЕ ИМПУЛЬСНОГО ЛАЗЕРНОГО ИЗЛУЧЕНИЯ ПЛОТНЫМИ АЭРОЗОЛЬНЫМИ ОБРАЗОВАНИЯМИ

И.В. Самохвалов, В.В. Брюханова

Томский государственный университет

В настоящее время для интерпретации данных лидарных экспериментов используется уравнение лазерного зондирования (УЛЗ), полученное с учетом только однократного рассеяния

,

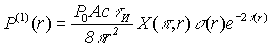(1)

где Р⁽¹⁾(r) - мощность однократно рассеянного назад излучения, поступающего на вход приемной системы лидара с расстояния r; P₀ - мощность посылаемого в атмосферу излучения; A - площадь приемной апертуры лидара; c - скорость света в воздухе; t _и - длительность импульса излучения лазера; X(p ,r) - индикатриса рассеяния в направлении 180° относительно зондирующего излучения; s (r) - объемный коэффициент рассеяния на расстоянии r; 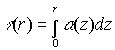t (r) - оптическая толщина на участке трассы от 0 до r; a (z) - объемный коэффициент ослабления, определяемый коэффициентами рассеяния s (r) и поглощения k (r): a (z)= s (r)+k (r).

При зондировании атмосферных аэрозолей длина волны l выбирается таким образом, чтобы поглощение было минимальным (k (r)<<s (r)). В дальнейшем будем считать излучение лазера квазимонохроматическим, работающим в спектральном интервале, где нет сильных линий атмосферных газов. При распространении излучения в плотных аэрозольных образованиях необходимо учитывать многократное рассеяние (МР). В этом случае сигнал обратного рассеяния можно представить как сумму интенсивностей всех кратностей рассеяния, поступающего на вход приемника

.

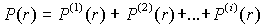(2)

Однако, расчет высших кратностей рассеяния (i>2) связан с большими трудностями как в плане физической формулировки задачи, так и в плане дальнейших вычислений интенсивностей по кратностям рассеяния.

Явление МР в аэрозольных средах в полной мере описывается уравнением переноса излучения, которое до сих пор в общем виде не решено. Есть ряд приближенных методов, среди которых наиболее распространенными являются методы Монте-Карло и малоугловое приближение. Эти методы дают достаточно хорошие результаты при решении прямой задачи, т.е. при расчете сигналов обратного рассеяния. В то же время интерпретация данных лазерного зондирования аэрозолями затруднена, т.к. невозможно проанализировать, как пространственная структура сигнала обратного рассеяния и интенсивности отдельных кратностей связаны с параметрами лидара и оптическими характеристиками среды. В настоящей работе эта задача решается последовательным учетом рассеяния первой и второй кратностей.

 

Схема формирования потока двукратно рассеянного назад излучения

Рассмотрим, как формируется поток двукратно рассеянного излучения на входной апертуре приемной системы моностатического лидара (см рисунок).

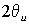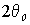Излучение источника, находящегося в точке О, направлено по трассе зондирования вдоль оси . Диаграмма направленности излучения источника определяется линейным углом , а поля зрения -. Причем, 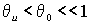. Будем считать, что оптические оси приемной и передающей антенн совмещены, что характерно для лидаров. Лазерный импульс представим в ви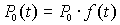де , где 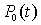- пиковая мощность лазера, 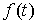- функция, описывающая форму импульса.

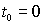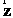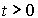Пусть в момент времени источник посылает импульс в направлении оси . Тогда для любого отраженный средой сигнал с расстояния 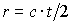можно представить в виде суммы потоков однократного (1) и многократного рассеяния (2). Поток двукратного рассеяния 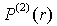складывается из элементарных потоков 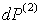, которые появляются при последовательном взаимодействии излучения с парами элементарных объемов среды 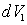и 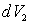. Причем объем 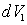расположен на оси зондирующего пучка в точке О₁, а 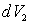- в точке М(z) (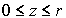), лежащей на дуге RN эллипса с фокальными точками О и О₁(z).

Для нахождения всего эхо-сигнала, обусловленного двукратно рассеянным излучением, необходимо просуммировать 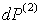по всему объему рассеивающей среды, ограниченному конической поверхностью с углом при вершине 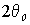и сферой радиуса OR=r (вершина конуса и центр сферы находятся в точке О). При этом необходимо учесть, что в момент времени 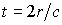на приемник поступает двукратно рассеянное излучение только от тех пар 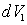и 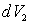, координаты которых удовлетворяют уравнению

,

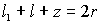(3)

где l₁ - расстояние от точки О до объема 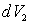, l - расстояние между объемам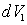и и .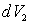

При фиксированном положении точки О и заданной дальности зондирования r соотношение (3) выполняется, если точки М(z), R и N будут находиться на поверхности эллипсоида вращения относительно оси OZ с фокусами в точках O и O₁(z). Сечение эллипсоида плоскостью, проходящей через ось OZ дает уравнение эллипса, имеющего в полярных координатах вид

,

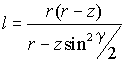(4)

где g - полярный угол, отсчитываемый против часовой стрелки от положительного направления оси OR₁.

Общее выражение для 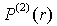получено ранее в виде [1]

,

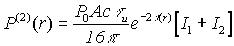(5)

где ,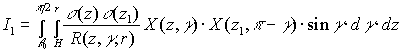

,

,

, .

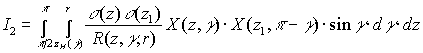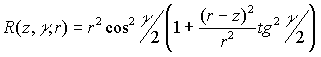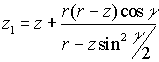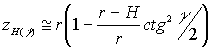Особенности формирования потока двукратно рассеянного излучения от удаленных аэрозольных образований

В плотных аэрозольных средах (например, в естественных облаках нижнего и среднего ярусов) мощность лидарного сигнала быстро затухает по мере распространения лазерного излучения в глубь среды. При зондировании таких сред глубина проникновения импульса в облака мала по сравнению с расстоянием до ближайшей границы аэрозольного образования Н

.

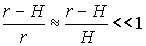(6)

В этом случае необходимо учитывать, что рассеивающий объем ограничен со стороны лидара плоскостью z=H, которая определяется в случае зондирования облаков с Земли нижней границей облаков, а при размещении лидара на космическом аппарате или самолете - верхней. Если выполняется условие (6) и

,

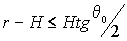(7)

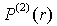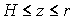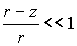то выражение (5) для можно существенно упростить. Прежде всего отметим, что и при в (5) .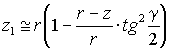

Теперь в (5) сделаем замену

,

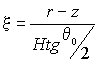(8)

а затем в выражении для 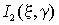еще раз перейдем к новым переменным

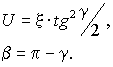
(9)

После этих подстановок оказывается, что интегралы в (5) для 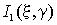и 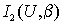идентичны. Поэтому (5) можно переписать в виде

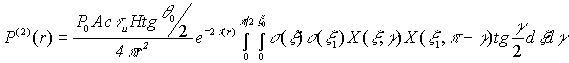
(10)

Здесь учтено, что 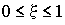, а

.

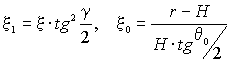(11)

Относительный вклад двукратного рассеяния по сравнению с однократным определяется как

.

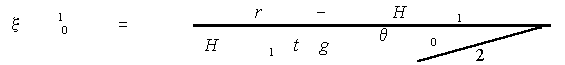(12)

Для однородного облака выполняется условие

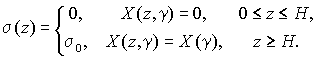
(13)

С учетом этого, выражения для мощности и относительного вклада двукратного рассеяния по сравнению с однократным принимают вид

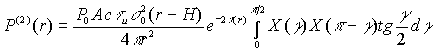
(14)

и

.

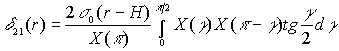(15)

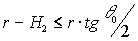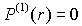Если облачный слой ограничен высотами H₁ и H₂, и при этом выполняется условие , то при r>H₂ мощность однократного рассеяния , а сигнал двукратного рассеяния

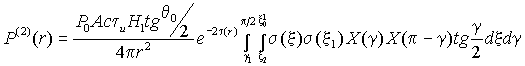, (16)

где , , .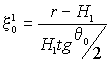

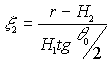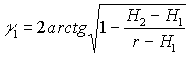Для однородного слоя ( s =const) при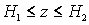 справедливо выражение

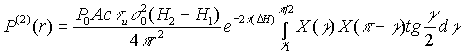, (17)

где t (D H)=s ₀(H₂-H₁) - оптическая толщина облачного слоя.

Таким образом, затяжка лидарного сигнала определяется второй кратностью рассеяния, а величина “хвоста” определяется формой индикатрисы рассеяния и толщиной слоя.

Если 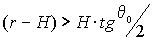, поперечный размер рассеивающего объема для второй кратности рассеяния определяется как границей среды, так и углом поля зрения приемной системы лидара.

Общее выражение для мощности лидарного сигнала, обусловленного двукратным рассеянием имеет вид

,

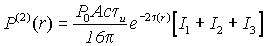(18)

где

,	(19)
	(20)
.	(21)

Здесь

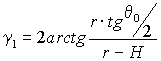,	(22)
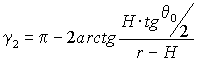,	(23)
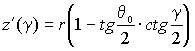,	(24)
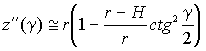.	(25)

Путем соответствующей замены можно показать, что выражение (16) при выполнении условий (6) сводится к следующему выражению

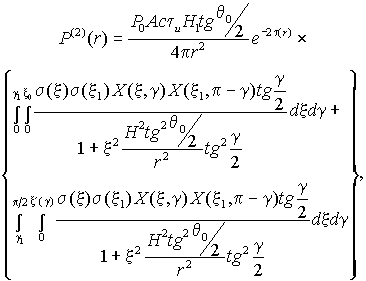
(26)

где , .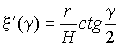

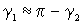Для однородного облака мощность сигнала обратного рассеяния для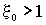

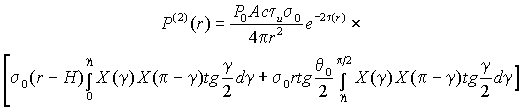
(27)

Как видно из полученного выражения, при 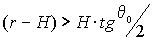величина эхо-сигнала двукратного рассеяния зависит как от глубины проникновения импульса в облако, так и от поперечного размера рассеивающего объема на расстоянии r.

 

Литература

Самохвалов И.В.//Изв. АН СССР. Сер.ФАО. 1979. Т15. №12. С. 1271-1279.