|
|
 |
 |

|
| |
АНАЛИЗ ВОЗМОЖНОСТИ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКИХ ПАРАМЕТРОВ БИОТКАНЕЙ ПО ПРОСТРАНСТВЕННЫМ ХАРАКТЕРИСТИКАМ РАССЕЯННОГО НАЗАД СВЕТА
С.П. Котова, А.М. Майорова, В.М. Петропавловский, М.А. Рахматулин
Самарский филиал ФИАН
Введение.
В настоящее время низкоинтенсивные лазеры широко используются для лечения различных заболеваний, например, большой опыт лечения сосудистых заболеваний и болезней печени накоплен в Самарском медицинском университете [1]. При этом широкое распространение получили терапевтические аппараты на полупроводниковых лазерах типа “Узор” и “Семикон”. Однако, оптические параметры, которые и определяют поведение светового поля внутри среды, на длинах волн полупроводниковых лазеров для большинства биотканей неизвестны. Информация об этих параметрах важна, во-первых, для задач дозиметрии. При этом, так как оптические коэффициенты биотканей в состояниях in vivo и in vitro различны [2], необходимы методики, позволяющие измерять эти параметры in vivo. Кроме того, неинвазивные (неразрушающие) методики определения оптических коэффициентов биотканей необходимы для задач диагностики. К таким методикам можно отнести методики определения оптических коэффициентов по рассеянному назад излучению, основанные на измерении пространственных характеристик излучения (в частности, проекционную методику и методику с использованием волокон для доставки и приема излучений). В настоящей работе методом Монте-Карло исследуется возможность использования транспортного приближения в методиках по рассеянному назад свету, а также численно и экспериментально определяется оптимальная для измерений область.
2. Численное моделирование.
К оптическим параметрам многократно рассеивающих сред (биотканей) относят коэффициенты поглощения m
a и рассеяния m
s и параметр анизотропии
g: 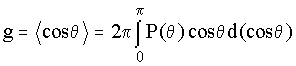 , ,
где P(q
) – фазовая функция рассеяния, которая для большинства биотканей хорошо аппроксимируется с помощью функции Хени-Гринштейна (1):
|
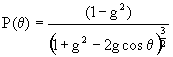
|
(1) |
На практике также часто используются коэффициент затухания m
t=m
a+m
s, длина свободного пробега L
=1/m
t и альбедо - m
s/m
t [3].
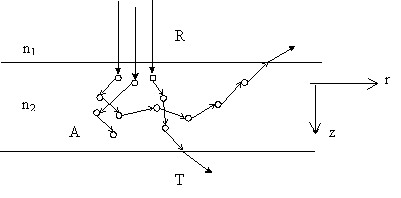
Если известны оптические параметры биотканей, а также показатель преломления n, то метод Монте-Карло, основанный на численном моделировании транспорта фотонов, позволяет рассчитать интегральные коэффициенты обратного рассеяния (R), поглощения (А) и пропускания (T), а также распределение излучения как внутри, так и вне биоткани (рис.1).
Достоинством метода Монте-Карло является возможность его использования для сред любой конфигурации (в том числе многослойных) с любыми граничными условиями. Кроме того, метод позволяет учесть как геометрию падающего излучения, так и геометрию приемника излучения (диаметр светочувствительной площадки, его угловую апертуру и т. д.). Основным недостатком метода Монте-Карло являются большие затраты машинного времени [2,3].
|
|
|
Рис.1. Моделирование транспорта фотонов методом Монте-Карло. |
Для ускорения расчетов часто используют, так называемое, транспортное приближение, в котором фазовая функция Хени-Гринштейна (1) заменяется упрощенной функцией Хени-Гринштейна (2):
|
P(q
)= [(1-g)+4gd
(cosq
-1)] |
(2) |
здесь первая часть описывает изотропное рассеяние, вторая - сильно вперед направленное рассеяние, на что указывает дельта-функция d
(cosq
-1). В результате на каждом шаге моделирования анизотропное рассеяние заменяется изотропным, а среда характеризуется транспортным коэффициентом рассеяния m
’s=m
s(1-g) [4].
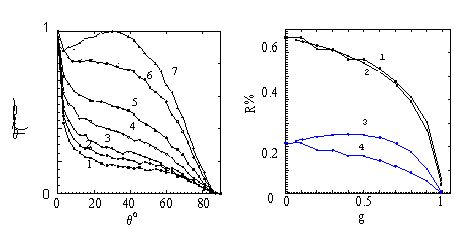
Уменьшение времени расчетов при использовании транспортного приближения и совпадение интегральных коэффициентов поглощения и рассеяния в обоих приближениях делают привлекательным использование транспортного приближения в методиках определения оптических параметров по пространственным характеристикам рассеянного назад света. С другой стороны, понятно, что замена на каждом шаге моделирования анизотропного рассеяния изотропным приводит к изменению углового распределения обратно рассеянного света. При этом и в проекционной методике, и в методике с использованием волокон важно значение угла, под которым фотон вылетает из среды. Отсюда возникает необходимость проверить возможность использования транспортного приближения в данных методиках. На рис.2 представлены графики интенсивности света, рассеянного назад, в зависимости от угла под которым фотон вылетает из среды для разных значений параметра анизотропии.
Из графиков видно, что по мере увеличения параметра анизотропии g все большее число фотонов вылетает из среды под меньшими углами к нормали. Это приводит к тому, что число фотонов, рассеянных назад, и число фотонов, попадающих в апертуру волокна, в транспортном и анизотропном приближениях совпадают лишь при больших и малых значениях параметра g (рис.3). Действительно, при малых значениях параметра g анизотропное рассеяние становится изотропным, а при больших g фазовая функция (1) наилучшим образом совпадает с фазовой функцией (2).
|
|
|
Рис.2. Зависимость интенсивности обратно рассеянного света от угла вылета фотонов из среды для разных g: 1- g=0,95; 2- g=0,9; 3- g=0,8; 4- g=0,7; 5- g=0,5; 6- g=0,3; 7- g=0,1. |
|
Рис.3. Зависимость интегрального коэффициента рассеяния R (1,2) и числа фотонов (3,4), попавших в угловую апертуру Rap (170) от параметра анизотропии g. Транспортное (1,4) и анизотропное (2,3) приближения. |
|
|
|
a |
b |
|
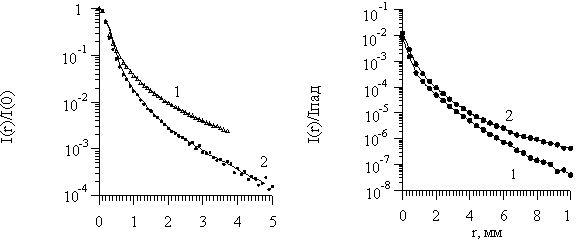
Рис.4. Зависимость относительной интенсивности I(r)/I(0) от расстояния до центра падающего пучка (a) и зависимость относительной интенсивности I(r)/Iпад от расстояния между центрами волокон (b) в транспортном (1) и анизотропном (2) приближениях (Iпад – интенсивность падающего пучка). |
Распределение интенсивности обратно рассеянного света в зависимости от расстояния от центра пучка падающего излучения (а) и расстояния между волокнами (b) в транспортном и анизотропном приближениях представлены на рис.4. Различие между кривыми (1) и (2) объясняется тем, что в транспортном приближении фотоны распространяются в среде и вылетают из неё под всевозможными углами, а в анизотропном приближении - под некоторым определенным набором углов к нормали. При этом в анизотропном приближении фотоны проникают глубже в среду и, следовательно, большая их часть поглощается, поэтому на рис.4(а) кривая, полученная в транспортном приближении, лежит выше кривой, полученной в анизотропном приближении. С другой стороны, в анизотропном приближении больше фотонов попадают в апертуру приемного волокна, и поэтому, на рис.4(b) анизотропная кривая лежит выше транспортной.
Таким образом, в методиках определения оптических параметров биотканей по пространственным характеристикам рассеянного назад света необходимо использовать анизотропное приближение.
Методом Монте-Карло в анизотропном приближении были просчитаны распределения интенсивности рассеянного назад света в зависимости от расстояния от центра падающего пучка для различных коэффициентов поглощения и рассеяния. Коэффициенты менялись относительно оптических параметров, характерных для печени белой крысы. Эти параметры, определенные на основе измерения интегральных коэффициентов рассеяния и пропускания, на длине волны 0.83 мкм составляют: m
а=0.15 мм-1, m
s’=0.725 мм-1, на длине волны 0.63 мкм - m
а=0.35 мм-1, m
s’=0.81 мм-1 [5]. Параметр анизотропии g брался равным 0.95 [6]. При расчетах учитывались ширина лазерного пучка w
=0.4 мм и скачок показателя преломления на границе воздух-печень n=1.4 [6]. Результаты расчетов представлены на рис.5.
|
|
|
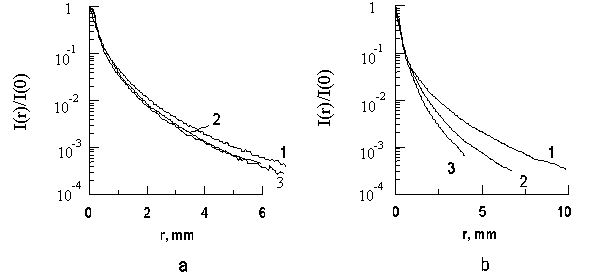
Рис.5. Интенсивности рассеянного назад света I(r)/I(0) в зависимости от расстояния от центра падающего пучка r для различных коэффициентов поглощения (a) и рассеяния (b). Значения m
a в мм-1 (a): 1 - 0.05, 2 - 0.15, 3 - 0.20 (m
s=4.5мм-1); значения m
s в мм-1 (b): 1- 4.5, 2- 14.5, 3- 24.5 (m
a=0.15 мм-1). |
Таблица 1.
Зависимость полуширины пятна рассеянного назад света от коэффициента поглощения (m
s=14.5мм-1)
|
m
a, мм-1 |
1/2 |
1/10 |
1/100 |
1/1000 |
|
D
r
, мм |
D
r
, мм |
D
r
, мм |
D
r
, мм |
|
0.05 |
0.21 |
0.65 |
2.15 |
5.15 |
|
0.07 |
0.21 |
0.60 |
2.05 |
5.00 |
|
0.10 |
0.21 |
0.65 |
2.00 |
4.95 |
|
0.15 |
0.21 |
0.60 |
1.93 |
4.70 |
|
0.17 |
0.21 |
0.60 |
1.90 |
4.40 |
|
0.20 |
0.21 |
0.60 |
1.80 |
4.40 |
В таблицах 1-4 представлены зависимости полуширины пятна рассеянного назад света по уровням падения интенсивности 1/2, 1/10, 1/100 и 1/1000 от оптических параметров биоткани. Таблицы 1-2 соответствуют оптическим параметрам на длине волны полупроводникового лазера, таблицы 3-4 – на длине волны He-Ne лазера.
Таблица 2.
Зависимость полуширины пятна рассеянного назад света от коэффициента рассеяния (m
a=0.15мм-1)
|
m
s, мм-1 |
1/2 |
1/10 |
1/100 |
1/1000 |
|
D
r
, мм |
D
r
, мм |
D
r
, мм |
D
r
, мм |
|
4.5 |
0.18 |
0.56 |
2.30 |
6.50 |
|
13.7 |
0.22 |
0.52 |
1.93 |
4.52 |
|
15.5 |
0.22 |
0.60 |
1.90 |
4.40 |
|
24.5 |
0.21 |
0.60 |
1.50 |
3.66 |
|
Таблица 3. Зависимость полуширины пятна рассеянного назад света от коэффициента поглощения (m
s=16.2 мм-1) |
|
Таблица 4. Зависимость полуширины пятна рассеянного назад света от коэффициента рассеяния (m
a=0.35 мм-1) |
|
m
a, мм-1 |
1/100 |
1/1000 |
|
m
s, мм-1 |
1/100 |
1/1000 |
|
D
r
, мм |
D
r
, мм |
|
D
r
, мм |
D
r
, мм |
|
0.10 |
1.90 |
4.60 |
|
|
|
|
|
0.15 |
1.83 |
4.22 |
|
8.0 |
1.65 |
4.00 |
|
0.25 |
1.60 |
3.90 |
|
11.0 |
1.63 |
3.90 |
|
0.30 |
1.57 |
3.70 |
|
16.2 |
1.54 |
3.62 |
|
0.35 |
1.54 |
3.62 |
|
18.0 |
1.50 |
3.55 |
|
0.45 |
1.45 |
3.40 |
|
21.0 |
1.43 |
3.40 |
|
0.55 |
1.40 |
3.20 |
|
24.0 |
1.36 |
3.22 |
|
0.60 |
1.27 |
3.00 |
|
27.0 |
1.30 |
3.18 |
Результаты расчетов показывают, что изменение параметров биоткани не приводит к значительному изменению ширины пятна рассеянного назад света по уровням 1/2 и 1/10. Таким образом, проекционная методика, в которой измерения проводятся на расстояниях, соответствующих спаду интенсивности в 2-10 раз, является малоинформативной. Изменения оптических параметров приводят к заметному изменению ширины пятна рассеяния по уровням спада интенсивности в 100 и 1000 раз. Отметим, что это соответствует расстояниям более 30 длин свободного пробега. Таким образом, оптимальной областью измерений в методике с использованием волокон для доставки и приема излучения является область расстояний более 30 длин свободного пробега. Естественно, что с другой стороны эта область ограниченна шумами.
Дополнительно была проанализирована зависимость между расстоянием от центра падающего пучка до точки вылета фотонов (r) и глубиной проникновения фотонов в среду. Для этого рассчитывалось, какое количество фотонов попадает в волокно, расположенное на фиксированном расстоянии от подающего волокна, при изменении толщины среды (d). Начиная с некоторого значения толщины слоя dнас, это количество фотонов выходило на насыщение, т.е. оставалось постоянным при дальнейшем увеличении d. Расчеты проводились для среды с оптическими параметрами m
s=40 мм-1, m
a=1 мм-1 и g=0,98, для разных расстояний между волокнами r. Результаты приведены в таблице 5, а также на рис.6.
Таблица 5.
Зависимость толщины среды, при которой наступает насыщение количества регистрируемых фотонов, от расстояния между волокнами
|
r, мм |
dнас, мм |
dнас/L
|
|
0 |
1,2±
0,2 |
49 |
|
0,4 |
1,8±
0,3 |
74 |
|
0,8 |
2,3±
0,3 |
94 |
|
1,6 |
2,8±
0,6 |
115 |
|
2,4 |
3,0±
0,7 |
135 |
Из таблицы и графика видно, что чем больше расстояние между волокнами, тем с более глубокой области среды приходят фотоны в точку детектирования. Данные выводы согласуются с результатами, полученными в работе [7], авторы которой доказали, что картины траекторий мигрирующих фотонов между входом в среду и точкой детектирования подчиняется так называемой “банановой форме”. Это означает, что в проекционной методике регистрируются фотоны, которые приходят с малых глубин (фотоны, не претерпевающие многократное рассеяние), в то время как методика с использованием волокон позволяет регистрировать фотоны, приходящие с больших глубин (фотоны, претерпевающие многократное рассеяние). Незначительное изменение размеров пятна рассеяния по уровням 1/2 и 1/10 и, одновременно, заметное изменение по уровням 1/100 и 1/1000 при варьировании оптических коэффициентов можно объяснить тем, что информацию о состоянии биоткани несут фотоны, которые претерпевают многократное рассеяние в среде.
|
|
|
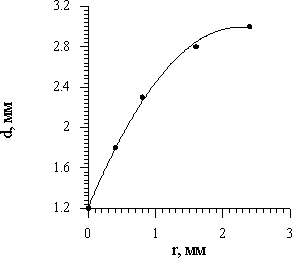
Рис.6. Зависимость толщины насыщения от расстояния между волокнами. |
Анализ таблиц 1-4 показывает также, что данная методика позволяет зафиксировать изменение параметров в 3 раза и более. Отметим, что такой чувствительности достаточно для диагностики заболеваний ряда биотканей, например, опухоли женской груди (m
а=0.06 см-1, m
s’=14.3 см-1 - для здоровой биоткани и m
а=0.33 см-1, m
s’=3.8 см-1- для опухоли на длине волны 0.625 мкм [8]). Однако, например, для диагностики опухоли бронхиальной ткани такая чувствительность явно недостаточна (m
а=1.2 см-1, m
s’= 240 см-1- для здоровой биоткани и m
а=1.8 см-1, m
s’= 207 см-1- для опухоли на длине волны 0.633 мкм [9]).
3. Экспериментальные исследования.
Экспериментальное исследование методик проводилось на модельных средах с известными оптическими параметрами. В качестве таких сред использовалось сухое молоко, разбавленное в дистиллированной воде. Коэффициенты поглощения молока и воды в видимой и ближней ИК областях составляют менее 10-3 мм-1. В качестве поглотителя использовались синие чернила. Оптические параметры приготовленных таким образом сред определялись с помощью хорошо известной методики по измеренным интегральным коэффициентам рассеяния (R), пропускания (T) и коллимированной компоненте пропускания (Tc) [10]. Рецепты приготовления сред и их оптические параметры приведены в таблице 6.
Таблица 6.
Рецепты приготовления сред и их оптические параметры.
|
№ смеси |
Сухое молоко, г |
вода
мл |
Чернила
капли |
R,
% |
T,
% |
Tc,
% |
m
a,
мм-1 |
m
s,
мм-1 |
g |
|
I |
30 |
100 |
0 |
84,0 |
14,7 |
29,3 |
0,005 |
24,5 |
0,77 |
|
II |
30 |
100 |
1 |
73,5 |
13,9 |
28,2 |
0.023 |
25,3 |
0,79 |
|
III |
30 |
100 |
2 |
62,1 |
12,5 |
27,1 |
0.045 |
26,1 |
0,81 |
|
III.1 |
30 |
150 |
2 |
55,5 |
17,0 |
28,0 |
0,037 |
25,4 |
0,87 |
|
III.2 |
30 |
200 |
2 |
64,4 |
19,3 |
33,6 |
0.026 |
21,8 |
0,86 |
|
IV |
30 |
100 |
3 |
59,7 |
11,8 |
26,5 |
0,069 |
26,5 |
0,81 |
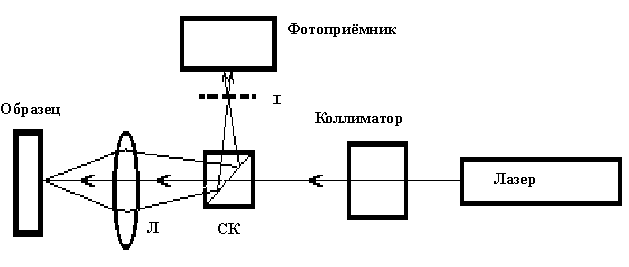
Экспериментальная установка для проекционной методики приведена на рис.7. Лазерный пучок (He-Ne, ЛГ-216) расширялся в коллиматоре К, проходил через светоделительный кубик СК и фокусировался на поверхность образца линзой Л (f=12 см, Æ
=8 см). Диаметр пучка в перетяжке был 50 мкм. Обратно рассеянный свет собирался той же самой линзой Л, которая формировала изображение пятна рассеянного света в плоскости I, где располагалась диафрагма фотоприёмника. Результаты измерений ширины пятна рассеянного назад света по уровню спада интенсивности 1/2 приведены в таблице 7.
Таблица 7
|
№ |
I |
II |
III |
III.1 |
III.2 |
IV |
|
2D
r
0.5, мм |
12±
0.01 |
0.10±
0.01 |
0.14±
0.01 |
0.16±
0.01 |
0.11±
0.01 |
0.12±
0.01 |
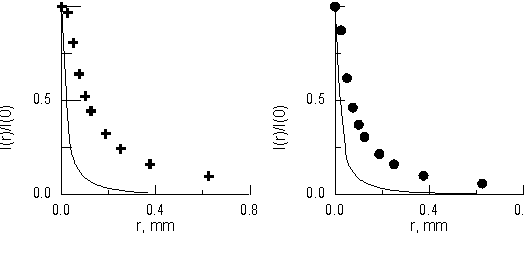
На рис.8 представлены зависимости интенсивности обратно рассеянного света от расстояния от центра пятна. Видно, что, во-первых, ширина пятна обратно рассеянного света слабо зависит от параметров среды, а, во-вторых, результаты эксперимента в 5 раз превышают результаты численных расчетов. Последнее, по-видимому, связано с тем, что в расчетах не учитывалась реальная передаточная функция линзы. Ширина пятна с учетом передаточной функцией линзы составляет ~300 мкм, что согласуется с экспериментом. Таким образом, экспериментальные результаты подтверждают малую информационность проекционной методики с точки зрения определения оптических параметров биоткани.
|
|
|
Рис. 7. Экспериментальная установка (проекционная методика). |
|
|
|
a |
b |
|
Рис.8. Зависимость интенсивности обратно рассеянного света от расстояния от центра пятна. Расчётная зависимость показана сплошной линией. a) - среда IV; b) - среда I. |
|
|
|
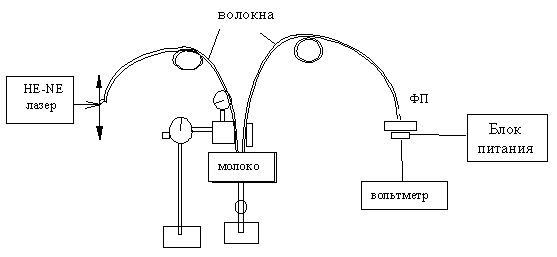
Рис.9. Экспериментальная установка (методика с использованием волокон для доставки и приема излучения). |
На рис.9 представлена экспериментальная установка для методики с использованием волокон. Излучение He-Ne лазера вводилось через микрообъектив в подающее волокно диаметром 400 мкм с угловой апертурой 350. Подающее и приемное волокна закреплялись в специально спроектированном держателе волокон. Минимально достижимое расстояние между центрами волокон »
1,2 мм. Держатель волокон позволяет перемещать волокна в горизонтальном и вертикальном направлениях. Передвижения фиксировались двумя микрометрическими часовыми механизмами. Волокна подводились к поверхности рассеивающей среды, которая находилась в кювете с размерами 2,7´
5´
7,7 мм. Приемное волокно (диаметр 400 мкм, апертура 350) собирало обратно рассеянное излучение, и доставляло его к фотоприемнику ФД-24. Перемещение приемного волокна в горизонтальном направлении позволяло осуществлять запись зависимости интенсивности обратно рассеянного света от расстояния между центрами волокон.
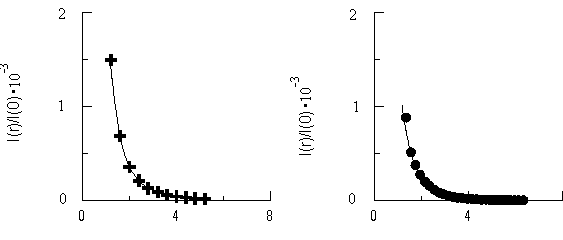
Данные зависимости для модельных сред I и IV представлены на рис.10. Для всех сред получено хорошее совпадение теоретических и экспериментальных зависимостей, что позволяет говорить об адекватности нашего моделирования.
|
|
|
a |
b |
|
Рис.10. Зависимость интенсивности обратно рассеянного света от расстояния между центрами волокон. Расчётная зависимость показана сплошной линией. a) среда IV; b) среда I. |
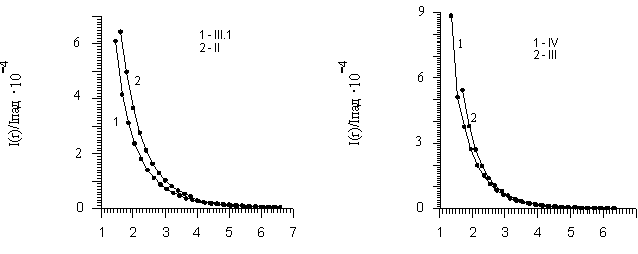
На рис.11 представлены графики зависимости интенсивности света, рассеянного назад, от расстояния между центрами волокон для разных сред.
|
|
|
Рис.11. Экспериментальные графики зависимости интенсивности обратно рассеянного света от расстояния между центрами волокон. |
Анализ графиков показывает, что, во-первых, методика с использованием волокон для доставки и приема излучения, позволяет зарегистрировать изменение коэффициента поглощения рассеивающей среды примерно в 1.5 раза, во-вторых, наиболее чувствительной является область расстояний между волокнами от 1.5 мм или 35 длин свободного пробега (что согласуется с численными расчетами). Видно, что с другой стороны эта область ограничена шумами. Таким образом, данную методику целесообразно использовать для определения параметров биотканей. При этом для определения оптических параметров достаточно провести измерения относительной интенсивности обратно рассеянного света в некоторых стационарных точках. Для чего возможно создать установку, в которой несколько волокон фиксируются на определенных расстояниях, оптимальных для проведения измерений.
4. Заключение.
В данной работе численно и экспериментально проанализирована возможность определения оптических параметров среды по пространственным характеристикам рассеянного назад света. Показано, что в таких методиках при численных расчетах необходимо использовать анизотропное приближение. Поскольку информацию о состоянии биоткани несут фотоны, претерпевающие многократное рассеяние, оптимальной областью для проведения измерений является область спада интенсивности обратно рассеянного света в 100, 1000 раз. Это соответствует расстояниям более 30 длин свободного пробега. С другой стороны эта область ограничена шумами. Таким образом, нецелесообразно применять проекционную методику. Методика с использованием волокон для доставки и приема излучения позволяет почувствовать изменение параметров в 3 и более раз, что достаточно для диагностики ряда заболеваний.
Работа выполнена при поддержке ФЦП “Интеграция” – проект 2.1-235.
Литература.
- Жуков Б.Н., Лысов Н.А. Лазерное излучение в экспериментальной и клинической ангиологии. Самара, 1996.
- W.-F. Cheong, S.A. Prahl, A.J. Welch ”A review of the optical properties of biological tissues”, IEEE Journal of Quantum Electronics, 26, No.12, pp.2166-2185,1990.
- Тучин В.В.”Исследование биотканей методами светорассеяния”, УФН., 167, №5, с.517-539, 1997.
- Словецкий С.Д. “Моделирование распространения оптического излучения в слоистой случайно-неоднородной среде методом Монте-Карло.” Радиотехника, №7, 1994.
- Бунькова Е.Б., Иванова А.М., Котова С.П. и др. “Распределение поглощенной энергии при воздействии низкоинтенсивного лазерного излучения на печень крысы.” Труды XXV школы-симпозиума по когерентной оптике и голографии. Ярославль, 1997, с.213-217.
- S. Jacques. “Optical properties of rat liver between 350 and 2200 nm.” Appl. Opt.,28, No.12, pp.2325-2330, 1989.
- N.C. Bruce “Experimental study of the effect of absorbing and transmitting inclusions in highly scattering media”, Appl. Opt., 33, No.28, pp.6692-6698,1994.
- Тучин В.В. Лазеры и волоконная оптика в биомедицинских исследованиях. Издательство Саратовского Университета, с.45, 1998.
- J.Qu, C.MacAulay, S.Lam and B.Palcic, “Optical properties of normal and carcinomatous bronchial tissue”, Appl.Opt., 33, No 31, pp.7397-7405, 1994.
B.Wilson, S.Jacques “Optical reflectance and transmittance of tissues: principles and applications”, IEEE J. of QE, 26, No 12, pp.2186-2199, 1990.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

