|
|
 |
 |

|
| |
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ИЕРАРХИЧЕСКИХ СИСТЕМ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ИЕРАРХИЧЕСКИХ СИСТЕМ
А.И. Литвин, С.Е. Секисова
Институт Оптического Мониторинга СО РАН, Томск
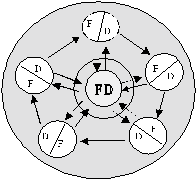
Жизнедеятельность практически всех больших сложных систем (биологических, экологических, социальных) сопровождается непрерывным потреблением продуктов "питания" (вещества, энергии, взаимодействие различного рода полей, информации - MEPI), необходимых для их существования. MEPI поступают из внешней среды некоторым способом в виде K - потоков с многократным их ветвлением. Транспортная система жизнеобеспечения этих организмов иерархически организована и содержит большое число уровней. Локальное изменение MEPI в некоторой точке системы является следствием перераспределения MEPI на всех предыдущих уровнях иерархии. Такое перераспределение приводит к изменению потоков и в соседних ветвях транспортной системы, т.е. в других точках системы. Этим действием вносятся возмущения в процессе жизнедеятельности системы, приводя его к хаотическому поведению. Заметим, что такого вида моделями систем являются модели "хищник-жертва", система циркуляции крови и др. Например, модель клеточной ткани высокоразвитых организмов, в которой через иерархическую сеть сосудов кровь снабжает кислородом все его ткани.
Такие модели можно представить в общем виде [1, 2],
|
|
где K -поток есть входной поток, представляющий расход MEPI, необходимый для развития данной системы и характеризует организм системы как "потребителя" ресурса или как "ресурс" или как "жертву". Таким образом, система представляется как совокупность элементов с введенными выше отношениями в виде целостной системы.
Целостная система - объединение, коллектив элементов (систем низших рангов), обладающих свойством вступать в устойчивое взаимодействие друг с другом, при котором и образуются новые структуры (целостные системы), характеризующие стремлением к самосохранению по содержанию, к самоповторению по форме (свойства фрактальности) [1-3]. Такое определение можно дополнить тем, что в понятие целостной системы должны входить не только образования новых структур, но и структур с большим числом уровней и связей, а также с самосовершенствованием самоорганизации на каждом уровне.
Основные свойства целостных систем подробно описаны в работах [1, 2].
В этом случае рассмотрим состояние элемента в виде некоторого поля u, которое характеризует концентрацию MEPI, служащею мерой интенсивности его жизнедеятельности.
Распределение поля удовлетворяет уравнению
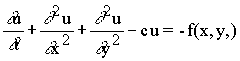 (1) (1)
где f - скорость генерации величины u, а член cu описывает скорость вывода продуктов MEPI из элемента транспортным потоком.
Для некоторых важных эллиптических задач дифференциальных уравнений в частных
производных разработаны быстрые прямые методы, которые подробно описаны в работах
[4-7]. Одним из этих методов является ортогональное дискретное преобразование
(ОДП) Фурье. Этот метод применим в задаче Дирихле для прямоугольной области
и основан на следующем [4-7]. Если число интервалов по каждой переменной 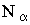 разбивается на множители, то вычислять коэффициенты ДПФ можно по экономичным
формулам. Если
разбивается на множители, то вычислять коэффициенты ДПФ можно по экономичным
формулам. Если 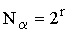 ,
то метод является особенно быстрым и требует всего ,
то метод является особенно быстрым и требует всего 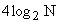 действий на каждый узел сетки.
действий на каждый узел сетки.
Рассмотрим этот метод сначала на примере одномерной задачи для уравнения Гельмгольца
с постоянными коэффициентами 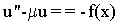 и краевыми условиями первого рода. Составим разностную схему на одномерной сетке
и краевыми условиями первого рода. Составим разностную схему на одномерной сетке
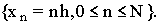 Тогда
Тогда
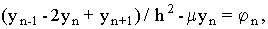
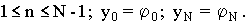 (1) (1)
Будем искать разностное решение в виде разложения в ряд Фурье
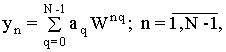 (2) (2)
где W=exp(2?
i/N).
Подставим выражение (2) в (1) и умножим на 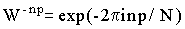 и просуммируем по n от 0 до N-1. Заметим попутно, что
и просуммируем по n от 0 до N-1. Заметим попутно, что 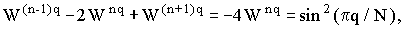 а также, учитывая условия ортогональности гармоник, найдем
а также, учитывая условия ортогональности гармоник, найдем
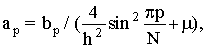 (3) (3)
где 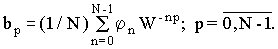 (4)
(4)
Формулы (3) и (4) являются неэкономичными. Для вычисления коэффициента 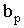 требуется 2N операций; для вычислений всех коэффициентов
требуется 2N операций; для вычислений всех коэффициентов 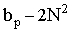 операций. Поэтому для вычисления вышеназванных коэффициентов необходимо использовать
алгоритм БПФ, так как в этом случае требуется всего 2Nlog2N
операций, что значительно сокращает время счета на ЭВМ.
операций. Поэтому для вычисления вышеназванных коэффициентов необходимо использовать
алгоритм БПФ, так как в этом случае требуется всего 2Nlog2N
операций, что значительно сокращает время счета на ЭВМ.
Обобщение этого метода на случай двух переменных очевидно.
Пусть для уравнения с постоянными коэффициентами
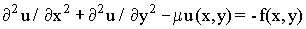 (5) (5)
поставлена первая краевая задача в прямоугольной области. Введем равномерную сетку {x n=nh1,ym=mh2,0?
n?
N, 0?
m?
M}, где N и M- числа, равные степеням двойки. Составим разностную схему:
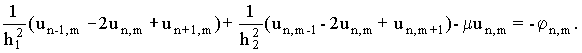 (6) (6)
Разностные решения будем искать в виде разложения в ряд Фурье [4-6]:
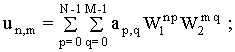 (7) (7)
где 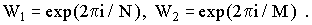
Коэффициенты Фурье будут иметь вид [4-6]:
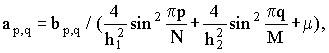 (8) (8)
где 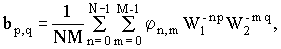 или
или 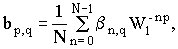
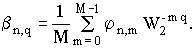 (9) (9)
Из решения (9) следует, что двумерная задача Дирихле для уравнения Гельмгольца с постоянными коэффициентами сводится к одномерной задаче. Это позволяет сводить многомерные задачи рассматриваемого вида уравнений к одномерным. Это следует из того, что ОДП (Фурье, Уолша, и др.) являются разделимыми преобразованиями [4-7].
Замечание 1. Вместо алгоритма БПФ можно использовать и другие алгоритмы, например, БПУП (быстрое преобразование Уолша-Пэли).
Замечание 2. Решение задачи Дирихле для уравнения Гельмгольца рассматривается в прямоугольной области, так как имеются процедуры сведения первой краевой задачи для уравнения Гельмгольца в области с криволинейной границей к краевой задаче в прямоугольной области, например, в [7].
Рассмотрим уравнение 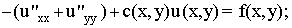
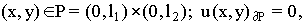 (3) (3)
где ?
P- граница прямоугольника, с(x,y)?
0.
В этом случае для решения этого уравнения можно воспользоваться итерационным неявным чебышевским методом [4-7]. Уравнение (3) представим в виде
Au=f, (4)
где А- линейный оператор. Уравнение (4) можно решить итерационным методом Чебышева [4-7]:
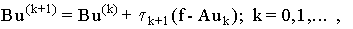 (5) (5)
где 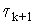 -
оптимальный параметр метода Чебышева. Обозначим: -
оптимальный параметр метода Чебышева. Обозначим:
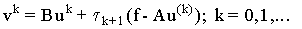 (6) (6)
решим СЛАУ 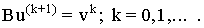 (7)
(7)
Оператор B можно найти следующим образом:
Положим 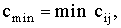 1?
i? N, 1? j?
M, где 1?
i? N, 1? j?
M, где 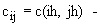 коэффициенты уравнения Гельмгольца. Пусть теперь
коэффициенты уравнения Гельмгольца. Пусть теперь 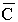 -
"диагональная" матрица размерности NM с коэффициентами cmin. Положим -
"диагональная" матрица размерности NM с коэффициентами cmin. Положим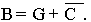 Тогда
выражение (7) примет вид: Тогда
выражение (7) примет вид:
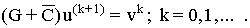 (8) (8)
Таким образом, решение системы (8) сводится к решению уравнения Гельмгольца с постоянными коэффициентами [4-7]. Число итераций в двухслойном методе Чебышева определяется по формуле [5-7]:
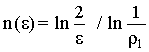 , (9) , (9)
где 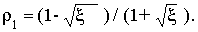 Так как ? >0 известно, то остается определить
величину ? ;
Так как ? >0 известно, то остается определить
величину ? ; 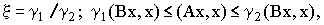 где в данном случае (x,y) определяет внутренне произведение. Величины
где в данном случае (x,y) определяет внутренне произведение. Величины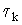 определяются: определяются:
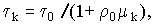 где
где 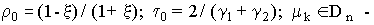 множества корней полиномов Чебышева первого рода
множества корней полиномов Чебышева первого рода 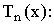
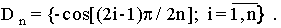
Пусть 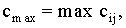 1?
i ? N, 1? j?
M; 1?
i ? N, 1? j?
M; 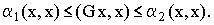
Теорема. Можно показать [6, 7], что 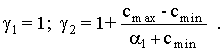 И
следует: И
следует:
Следствие. 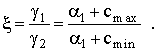 Пусть для уравнений с постоянными коэффициентами
Пусть для уравнений с постоянными коэффициентами  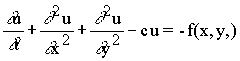 (10)
(10)
поставлена начально-краевая задача в прямоугольной области: 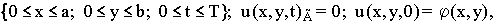 где Г- граница прямоугольной области.
где Г- граница прямоугольной области.
Для решения задачи (10) применим следующий прием [7]. Зафиксируем 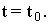 Рассмотрим сначала задачу Дирихле для уравнения Гельмгольца:
Рассмотрим сначала задачу Дирихле для уравнения Гельмгольца:
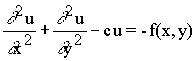 , (11) , (11)
решение которой приведено выше. Ввиду того, что уравнение (10) является параболическим,
решение u(x,y,t) на слое 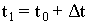 может быть определено, если известны его значения в предыдущем слое
может быть определено, если известны его значения в предыдущем слое 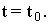 Дискретное преобразование Фурье от уравнения (10) представим в виде:
Дискретное преобразование Фурье от уравнения (10) представим в виде:
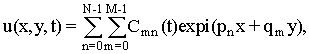 (12) (12)
где величины 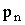 и и
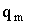 равны:
2? n/a; 2?
m/b; равны:
2? n/a; 2?
m/b; 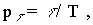 ?
=0,...,L-1, где L- число точек деления
сетки по переменной t. ?
=0,...,L-1, где L- число точек деления
сетки по переменной t.
Подставляя выражение (12) в уравнение (10), получим:
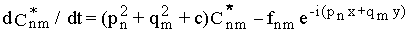 . (13) . (13)
Уравнения (13) - линейные уравнения относительно переменных
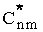 . . 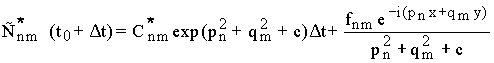
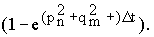 (14) (14)
Решение u(x, y, t 0+? t)
следует из обратного преобразования Фурье, использующего известные коэффициенты
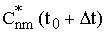 [7]. [7].
В случае переменного коэффициента в уравнении (10) вместо постоянного коэффициента с в выражении (14) нужно проставить соответствующее значение с(х, у).
Таким образом, в рассмотренной выше модели процессы жизнедеятельности различных точек являются локальной функцией поля u, тем самым они функционируют независимо друг от друга (без учета диффузионного взаимодействия). Это свойство позволяет считать такие системы системами с саморегуляцией. Например, в результате адаптации системы к изменившимся условиям внешней среды изменяется и интенсивность деятельности элементов системы на различных иерархических уровнях, что сказывается на изменении локального поля u. Увеличенная концентрация MEPI свидетельствует об ускорении интенсивности процессов жизнедеятельности, что требует увеличение потока транспортной сети. Конечно, в природе трудно найти такие системы с идеальным процессом адаптации. Нарушение процесса саморегуляции влечет устранение подобия подсистем, что может служить причиной разрушения систем. Но в природе часто существуют дополнительные связи между уровнями иерархии, подавляющие неидеальности. Отсюда следует, что может существовать синергетический механизм регуляции систем, который использует индивидуальный отклик каждого элемента системы на малую часть информации и позволяет каждому элементу системы функционировать идеально на достаточно больших промежутках времени.
- Поздняков А.В. // Проблемы самоорганизации. В. № 3: Самоорганизация геоморфосистем. Томск, 1996. - С. 15-24.
- Поздняков А.В. Третий путь развития.-Российская модель. Томск:1997.-76с
- Федер Е. Фракталы. - М.: Мир, 1991. - 260 с.
- Калиткин Н.Н. Численные методы. - М.: Наука, 1976. - 512с.
- Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. - М.: Наука, 1987. - 592 с.
- Коваленко И.Л., Ленивцева Л.Ю., Литвин А.И., Симонженков C. Д. //ЖВМ и МФ. - 1995. - Т
. 3,. № 6. - С. 611-615.
Литвин А.И., Солдатов В.Н. // Методы и алгоритмы параметрического анализа линейных и нелинейных моделей переноса. - М.: МГЗПИ, 1985, В. № 3. - С. 148-153.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

