|
|
 |
 |

|
| |
ИССЛЕДОВАНИЕ СДВИГОВОЙ УПРУГОСТИ СМЕСЕЙ ПРИРОДНЫХ ПОЛИМЕРОВ
ИССЛЕДОВАНИЕ СДВИГОВОЙ УПРУГОСТИ СМЕСЕЙ ПРИРОДНЫХ ПОЛИМЕРОВ
Б.Б. Дамдинов, Б.Б. Эрдынеев*
Отдел физических проблем БНЦ СО РАН, *Бурятский объединенный институт природопользования БНЦ СО РАН
Изучение физических и химических смесей полимеров открыло новые области исследований и решения практических задач. Смешение полимеров во многом аналогично сополимеризации, как способу достижения заданных свойств химических структур. Разница состоит в том, что смешение позволяет достичь этой цели физическим, а не химическим путем.
Ранее [1] было показано, что различные жидкости не зависимо от вязкости и полярности обладают измеримым значением действительного модуля сдвига G’ при частоте 74 кГц. Исследования сдвиговых свойств жидкостей проводились резонансным методом [2] с использованием пьезокварцевого резонатора. Суть данного метода, вкратце, заключается в следующем. Пьезокварцевый кристалл, колеблющийся на основной резонансной частоте, контактирует своей горизонтальной поверхностью с прослойкой жидкости, накрытой твердой накладкой. Накладка с прослойкой жидкости находится на одном из концов пьезокварца. При этом прослойка жидкости испытывает деформации сдвига и в ней должны установиться стоячие сдвиговые волны. В зависимости от толщины прослойки жидкости изменяются параметры резонансной кривой пьезокварца. Теория метода дает следующее выражение для комплексного сдвига резонансной частоты колебательной системы [2]:
|
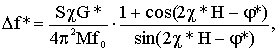
|
(1) |
где 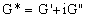 - комплексный модуль сдвига жидкости,
S - площадь основания
накладки, ? * -
комплексное волновое число, H
- толщина жидкой прослойки, f0 -
резонансная частота, ? *
- комплексный сдвиг фазы при отражении
волны от границы жидкость-накладка.
- комплексный модуль сдвига жидкости,
S - площадь основания
накладки, ? * -
комплексное волновое число, H
- толщина жидкой прослойки, f0 -
резонансная частота, ? *
- комплексный сдвиг фазы при отражении
волны от границы жидкость-накладка.
Выражение (1) предельно упрощается для случая, когда толщина пленки жидкости много меньше длины сдвиговой волны, а накладку можно считать практически покоящейся. В этом случае расчетная формула сдвиговой упругости имеет вид:
|
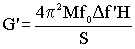 , ,
|
(2) |
где M- масса пьезокварца, ?
f’ - действительный сдвиг частоты. Тангенс угла механических потерь
|
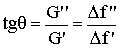
|
(3) |
где мнимый сдвиг резонансной частоты ?
f’’ равен, по определению, половине изменения ширины резонансной кривой. Экспериментально измеряемыми величинами были: толщина прослойки жидкости, сдвиг резонансной частоты и изменение ширины резонансной кривой пьезокварца. По найденным величинам, по формулам (2) и (3), вычислялись основные вязкоупругие свойства жидкостей динамический модуль сдвига G' и тангенс угла механических потерь tg?
, равный отношению мнимого модуля G'' к действительному G'. G'' является мерой той части энергии упругих колебаний, которая превращается в тепло, т.е. G'' характеризует диссипацию энергии колебаний в вязкоупругом теле.
В данной работе были исследованы сдвиговые свойства смесей природных полимеров резонансным методом. В качестве объектов исследования были выбраны природные полимеры: коллаген и карбоксиметилцеллюлоза (КМЦ). В первую очередь были найдены значения G’ и tg?
для исходных компонентов смеси (2% растворов коллагена и КМЦ в воде). Затем исходные компоненты смешивались в различных соотношениях и определялись те же параметры. В таблице представлены результаты исследования смесей коллагена с КМЦ в зависимости от соотношения в бинарной смеси.
Таблица
|
Состав смеси
Коллагена и КМЦ |
t, ос |
G’?
10-6 , дин/см2 |
tg?
|
|
0:1
1:10
1:6
1:5
1:4
1:3
1:2
1:1
2:1
3:1
1:0 |
19.1
20.0
18.8
17.8
18.3
18.2
19.0
19.5
19.1
20.0
17.5 |
0.803
0.344
0.248
0.229
0.227
0.232
0.266
0.334
0.442
0.515
0.645 |
0.139
0.243
0.357
0.398
0.456
0.430
0.293
0.241
0.238
0.230
0.180 |
Как видно из таблицы значения действительного модуля низкочастотной сдвиговой упругости равны 0.803?
106 дин/см2 и 0.645?
106 дин/см2 для КМЦ и коллагена, соответственно. При смешивание этих двух компонентов с различными соотношениями мы видим, что значения модуля упругости проходят через минимум при составе смеси 1:4 частей коллагена к КМЦ, а значения тангенса угла механических потерь проходят через максимум при этом же составе смеси. Если предположить, что поведение смеси описывается с помощью простых моделей, состоящих из двух компонентов с различными модулями упругости, например модель Такаянаги [3], то для такой модели справедливо следующее соотношение:
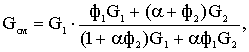 (4) (4)
где G 1 и G2 - модули упругости компонентов, ф1 и ф2 - объемные доли компонентов в смеси, ?
- постоянный параметр, выбранный нами равным 0.857. Из формулы (4) видно, что для такой модели модуль упругости смеси будет равномерно уменьшаться от G1 до G2. Видно, что экспериментальные результаты расходятся с значениями модуля упругости, вычисленного по модели. В модели предполагается, что смесь является чисто физическим соединением компонентов. Поэтому можно предположить, что в данной смеси при определенном соотношении, а именно 1:4 коллагена к КМЦ, происходят химические взаимодействия. Выбор КМЦ был обусловлен тем, что в соединительных тканях коллаген связан с полисахаридами, образовывая белково-углеводные комплексы.
Проведенные исследования показали, что для описания зависимости модуля упругости от состава смеси недостаточно применения чисто механических моделей. Для полного выяснения сдвиговых свойств смесей полимеров необходимо исследование в зависимости от частоты и температуры.
Работа выполнена при финансовой поддержке РФФИ (грант № 98-01-00503).
Литература
У.Б. Базарон, Б.В. Дерягин, А.В. Булгадаев, ДАН СССР , 166, 639, (1966).
У.Б. Базарон, Б.В. Дерягин, А.В. Булгадаев, ЖЭТФ, 51, 969, (1966).
Полимерные смеси, под ред. Д. Пола и С. Ньюмена, М.: Мир, 400, (1981).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

