|
|
 |
 |

|
| |
ВЯЗКОСТЬ ЖИДКОСТЕЙ ПРИ МАЛЫХ ГРАДИЕНТАХ СКОРОСТИ ТЕЧЕНИЯ
ВЯЗКОСТЬ ЖИДКОСТЕЙ ПРИ МАЛЫХ ГРАДИЕНТАХ СКОРОСТИ ТЕЧЕНИЯ
У.Б. Базарон , Б.Б. Бадмаев, Т.С. Дембелова, Е.Р. Очирова
Отдел физических проблем БНЦ СО РАН
По современным представлениям релаксация упругих сдвиговых напряжений в жидкостях связана со структурной перестройкой ближайшего окружения жидкости и происходит за время, равное времени самодиффузии молекул (10-8 - 10-12 с). Обычно считается, что динамическая сдвиговая упругость жидкостей должна быть одного порядка с значением ее величины в твердом состоянии, поскольку в связи с незначительным изменением объема при плавлении силы взаимодействия между частицами жидкости не претерпевают больших изменений [1]. Исходя из этого, можно оценить максвелловское время релаксации по известной формуле ?
=?
/G'. Если положить G' = 1010 дин/cм2, то для периода релаксации воды получим значение ?
= 10-12 сек. Именно поэтому было неожиданным обнаружение сдвиговой упругости у жидкостей резонансным методом с применением пьезокварцевого кристалла при частоте порядка 74 кГц в работах [2-3]. В начале эксперименты были поставлены с целью исследования физических свойств тонких граничных слоев жидкостей. Однако полученные результаты показали, что сдвиговая упругость присуща жидкости в объеме. Таким образом, эксперимент опровергает значения периода релаксации сдвиговых напряжений, полученных на основании рассмотрения скорости самодиффузии. Наличие сдвиговой упругости у жидкостей при низких частотах говорит о существовании в них низкочастотного вязкоупругого релаксационного процесса. По-видимому, в жидкостях в ряде случаев могут иметь решающее значение коллективные эффекты, зависящие от взаимного расположения и взаимодействия больших групп молекул. Релаксация неравновесного состояния конфигурации большого коллектива частиц требует согласованного перемещения и изменения ориентации многих молекул. Поэтому время релаксации таких коллективных неравновесных состояний может намного порядков превышать время оседлого существования отдельных молекул. Можно предположить, что именно с этим обстоятельством связано существование низкочастотной сдвиговой упругости у жидкостей.
Исследования сдвиговой упругости с учетом затухания [4] показали, что тангенс угла механических потерь у обычных маловязких жидкостей намного меньше единицы. Так например, у воды tg?
=0.3, у бутилового спирта tg?
=0.18. Модули сдвига у этих жидкостей соответственно равны 0.31?
106 дин/см2 и 1.03?
106 дин/см2.
Если считать, что молекулярный аспект процессов, ответственных за наличие сдвиговой упругости в жидкостях, аналогичен максвелловской релаксации, при которой скорость исчезновения упругого напряжения, вследствие перегруппировок молекул пропорциональна величине напряжения сдвига, то характерная частота релаксации этих жидкостей должна быть меньше частоты эксперимента.
В работах [5-6] было показано, что при малых углах сдвиговой деформации комплексный модуль сдвига остается постоянным, напряжение в пленке жидкости оказывается пропорциональным величине деформации. При дальнейшем возрастании угла деформации модуль сдвига уменьшается, а мнимый модуль сдвига проходмт через максимальное значение. Такое поведение можно объяснить тем, что при увеличении сдвиговой деформации происходит разрушение равновесной структуры жидкости, вследствие чего средняя релаксационная частота вязкоупругого процесса сдвигается в область высоких частот. В работе [6] было предположено, что при равновесной структуре эффективная вязкость может оказаться намного больше табличной вязкости, которая относится к жидкости с разрушенной пространственной структурой, соответствующей ламинарному течению жидкостей.
В случае реологической модели Максвелла эффективная вязкость ?
ef и частота релаксации frel определяются по следующим формулам:
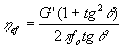 , (1) , (1)
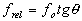 , (2) , (2)
где fo - частота эксперимента, в нашем случае равная 73.5 кГц. Для воды и бутилового спирта при малых углах сдвиговой деформации эти формулы дают соответственно следующие значения: 2.4 Пз и 22 кГц для воды, 22.5 Пз и 7 кГц для бутилового спирта. Можно видеть, что рассчитанные значения вязкости намного больше табличных, а частоты релаксации меньше частоты эксперимента. По мере увеличения сдвиговой деформации вязкость уменьшается, стремясь к величине табличной вязкости. Все обычные жидкости дают аналогичную картину.
Из данного факта можно предположить, что табличная вязкость относится к жидкости с полностью разрушенной пространственной структурой соответствующей ламинарному течению в обычных вискозиметрах, и что вязкость жидкости в “покое” должна быть значительно большей, поскольку ее структура полностью восстанавливается. Поэтому представляет большой интерес возможность прямого измерения повышенной вязкости жидкостей с неразрушенной равновесной структурой.
Были поставлены предварительные эксперименты по измерению вязкости жидкостей при предельно малых градиентах скорости течения, когда можно было ожидать, что при элементарных актах вязкого течения структура жидкости мало изменяется. Наиболее удобным и простым оказался метод измерения, при котором исследуемая жидкость перетекала из одного сосуда в другой по длинному капилляру под действием создаваемой в них разности уровней, причем сечение первого сосуда примерно в 100 раз было меньше второго. Последнее обстоятельство позволяло пренебрегать изменением уровня во втором сосуде. Сосуды герметично закрывались и между собой имели воздушное сообщение. Установка располагалась на специальном фундаменте, изолированном от пола здания, чтобы исключить возможные вибрации установки. Разность уровней в сосудах измерялась вертикальным катетометром путем наблюдения увеличенной дифракционной картины от границы мениск жидкости - воздух с точностью ?
1 мкм. Кроме того, оба сосуда сообщались широкой стеклянной трубкой с краном, при помощи которого уровни жидкостей в сосудах могли выравниваться.
Легко показать, что между разностью уровней ?
H в сосудах и временем t существует следующая зависимость:
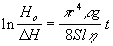 , (3) , (3)
где Ho - разность уровней в начальный момент времени, r - радиус капилляра, l - его длина, ?
- плотность жидкости, S - площадь сечения малого сосуда, из которого вытекает жидкость. Был применен капилляр длиной 100 и диаметром 0.1 см., а площадь сечения малого сосуда составляла 2.5 см2. Из выражения (3) следует, что если вязкость жидкости при всех градиентах скорости течения остается постоянной, то зависимость ln(Ho/?
H) от времени должна быть линейной. Если же при малых градиентах скорости течения вязкость будет повышаться, то мы будем наблюдать отклонение от этой зависимости.
Порядок проведения эксперимента был следующий. При открытом кране установка термостатировалась. Температура термостатирования поддерживалась близкой к температуре помещения. Затем кран закрывался и отсосом жидкости пипеткой из большого сосуда создавалась желаемая разность уровней. Сначала измерялось положение уровня в большом сосуде, а изменение уровня в малом сосуде фиксировалось через каждые 10-15 минут. В конце эксперимента, который обычно длился несколько часов, сообщающий кран открывался и замерялись положения уровней в обоих сосудах при их выравнивании. Отсутствие влияния испарения, а также капиллярно- и термоосмотических потоков проверялось по сохранению положения менисков жидкости при отсутствии разности уровней в сосудах.
Исследования показали, что зависимость l g(Ho/?
H) от времени при больших градиентах скорости течения линейная. Однако, начиная с определенного значения разности уровней, наблюдается все большее отклонение от линейной зависимости, что свидетельствует о повышении наблюдаемой вязкости. Для воды отклонение от линейности начинается при разности уровней в 22 мкм, для бутилового спирта при 75 мкм. Обратная величина угла наклона каждой точки к кривой пропорциональна вязкости. К концу эксперимента значение вязкости бутилового спирта увеличивается примерно в три раза. Аномалию вязкости обнаруживают также такие жидкости как гексадекан, ундекан, спирты и ряд других жидкостей. Измерения проводились при постоянной (комнатной) температуре. В дальнейшем предполагается измерение вязкости при различных температурах.
Результаты экспериментов по измерению аномальной вязкости при малых градиентах скорости течения жидкости и ранее обнаруженная сдвиговая упругость жидкостей при частоте колебаний 74 кГц свидетельствуют о существовании в них низкочастотного вязкоупругого релаксационного процесса в жидкостях, обусловленного коллективными взаимодействиями больших групп молекул. Отклонения от ньютоновского поведения представляют большой интерес для изучения проблемы структурной релаксации жидкостей. Рассмотренное явление может иметь важное практическое приложение во всех процессах, где преобладают медленные течения. Например, в грунтоведении и почвоведении, в частности, для объяснения явления морозного пучения грунтов, при процессах фильтрации жидкостей и растворов через искусственные и естественные мембраны.
Работа выполнена при финансовой поддержке РФФИ (грант N98-01-00504).
Литература
- Я.И. Френкель, Кинетическая теория жидкостей М.-Л. (1959).
- У.Б. Базарон, Б.В. Дерягин, А.В. Булгадаев, ДАН СССР
166, 639 (1966).
У.Б. Базарон, Б.В. Дерягин, А.В. Булгадаев, ЖЭТФ 51, 969 (1966).
У.Б. Базарон, Б.В. Дерягин, О.Р. Будаев, ДАН 205, 1326 (1972).
Б.Б. Бадмаев, У.Б. Базарон, О.Р. Будаев, Коллоидный журнал 44,841 (1982).
К.Т. Занданова, Б.В. Дерягин, У.Б. Базарон и др. ДАН 215, 309 (1974).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

