|
|
 |
 |

|
| |
ПАРАМЕТРЫ ТЕОРИИ СВОБОДНОГО ОБЪЕМА МЕТАЛЛИЧЕСКИХ СТЕКОЛ
С.Ш. Сангадиев, С.С. Бадмаев, А.Б. Баинова
Бурятский государственный университет,
Введение
В настоящее время для аморфных полимеров и низкомолекулярных органических и неорганических стекол установлена универсальность значения доли флуктуационного свободного объема fg при температуре стеклования Tg (см. [1-3]):
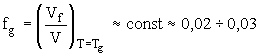 . (1) . (1)
В табл.1 в качестве примера приводятся значения fg для ряда аморфных полимеров и неорганических стекол. Как видно, fg является практически постоянной величиной. Соотношение (1) рассматривается как критерий стеклования жидкостей.
Представляет интерес расчет fg для металлических стекол (аморфных сплавов). Следует ожидать, что для них величина fg будет такого же порядка, что и для других стеклообразных систем, ибо по физическому смыслу доля флуктуационного свободного объема fg является универсальной характеристикой всех аморфных стеклообразных твердых тел и их расплавов [1-4].
В данной работе предлагается оценка доли флуктуационного свободного объема и других характеристик для ряда металлических стекол.
Теоретическая часть
У большинства металлов и других твердых тел увеличение объема при плавлении составляет около 2¸
4%. В дырочной теории жидкостей под свободным объемом подразумевается такой избыточный объем, равный суммарному объему дополнительных дырок, возникающих при плавлении кристалла [4]
V – V0 = vh Nh ,
где V0 – объем жидкости при отсутствии дополнительных дырок, vh – объем дырки, близкий к объему частицы, Nh – число избыточных дырок. Этот избыточный свободный объем замораживается при переходе из жидкого в твердое стеклообразное состояние. Поэтому в соответствии с известными идеями Я.И. Френкеля [4] в аморфных твердых телах, как и в жидкостях, существует свободный объем, обусловленный увеличением объема при плавлении кристалла [4-6]. Объемную долю свободного объема жидкости 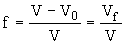 можно оценить (при 20 0С) путем сравнения значений упругих модулей объемного сжатия жидкости и газа. Формула изотермического модуля всестороннего сжатия жидкости, следующая из дырочной теории [4] можно оценить (при 20 0С) путем сравнения значений упругих модулей объемного сжатия жидкости и газа. Формула изотермического модуля всестороннего сжатия жидкости, следующая из дырочной теории [4]
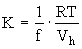 (2) (2)
(Vh – молярный объем дырок, R – газовая постоянная), аналогична выражению для давления газа P=RT/V, которое, как известно, численно равно его модулю объемного сжатия Кг. В приближенных оценках отношение RT/Vh можно принять за величину Кг. Давление газа, обладающего плотностью жидкости, имеет порядок величины: Р = Кг »
300 МПа (3×
109 дин/см2), тогда как фактический модуль объемного сжатия в случае жидкости равен, примерно, К»
104 МПа (1011 дин/см2). На основе этих данных Френкель приходит к следующему приближенному значению доли свободного объема жидкости [4, с.187]
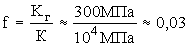 , (3) , (3)
которое практически совпадает с приведенным выше относительным увеличением объема при плавлении твердых кристаллических тел: D
V/V»
0,02¸
0,04.
Таким образом, в аморфном стеклообразном состоянии, представляющем собой в первом приближении состояние переохлажденной жидкости, существует свободный объем, состоящий из дефектов в виде дырок микроскопических масштабов. Данный свободный объем не накладывает ограничений на структурную модель собственно аморфного состояния, поскольку он рассматривается в качестве дефекта, а не структурного элемента. Удаление избыточного свободного объема не приводит к какому-либо кардинальному изменению симметрии и топологических характеристик аморфного состояния. Именно такой избыточный свободный объем, который в настоящее время чаще называют флуктуационным свободным объемом (см. [1-3]), является ответственным за изменение физических свойств аморфных твердых тел и их расплавов [1-9]. Что касается классического вандерваальсова свободного объема VF = V–b, где b – занятый атомами объем, то он представляет собой элемент структуры и входит в состав атомных комплексов, определяющих топологические и композиционные характеристики аморфного состояния. Иногда его называют геометрическим [2], структурно–обусловленным [5,6] свободным объемом, который не играет заметной роли в вязкоупругих свойствах стеклообразных систем. Объемная доля вандерваальсова свободного объема VF / V »
0,25¸
0,30, определенная по плотности упаковки атомов (см. [2]), на порядок превышает долю избыточного (флуктуационного) свободного объема fg »
0,02¸
0,03 при температуре стеклования.
Обычно величину fg вычисляют с помощью уравнения Вильямса–Ландела–Ферри (ВЛФ) на основе данных о температурной зависимости времени релаксации t
(Т) или вязкости h
(Т) в области стеклования [1,2]
Табл.1
Постоянные уравнений ВЛФ и параметры теории флуктуационного свободного объема для аморфных полимеров и неорганических стекол [2,3,4,8]
|
Стекло |
Tg,
K |
c1 |
c2,
K |
fg |
a
f ×
104 |
D
a
×
104 |
e
h , |
U¥
, |
Ug , |
|
1/ град |
кДж/моль |
|
Поливинилацетат
Натуральный каучук
Метакрилатные полимеры этиловый
n–бутиловый
n–октиловый |
305
300
335
300
253 |
35,9
38,4
40,5
39,1
37,0 |
46,8
53,6
65,5
96,6
107,3 |
0,028
0,026
0,025
0,026
0,027 |
5,9
4,8
3,7
2,6
2,5 |
5
4
3
3
2,5 |
9,2
9,2
10,5
9,2
7,5 |
14
17
22
31
33 |
91
96
113
97
78 |
|
Na2O–SiO2
Na2O, мол. % 19,0
32,9
44,8
К2O–В2O3
К2O, мол. % 0
2,1
8,5
23,5
34,4
Na2O–GeO2
Na2O, мол. % 5
25 |
746
704
667
578
586
623
712
701
729
755 |
38
36
44
29,6
29,7
33,4
36,0
38,4
40,0
40,0 |
317
275
211
121,4
89,0
116,9
140,4
142,1
220
160 |
0,026
0,028
0,023
0,034
0,034
0,030
0,028
0,026
0,025
0,025 |
0,86
1,03
1,08
2,9
3,8
2,6
2,0
1,8
1,1
1,6 |
–
0,86
1,39
–
–
–
–
–
–
– |
22,6
20,9
20,9
16,3
16,5
18,4
21,2
21,2
22,6
23,4 |
100
83
78
30
22
32
42
45
73
53 |
235
210
244
142
144
173
213
223
242
250 |
|
Na2O–PbO–SiO2
Na2O–CaO–SiO2
Se
NaPO3–ZnSO4
ZnSO4, мол. % 0
20
30
GeS2–GeBr4
GeBr4, мол. % 0
7,5
As40S60
As37S47Br16
As33S33Br33
Al2O3–K2O–P2O5
Al2O3–K2O–P2O5––Nb2O5 |
761
833
303
523
505
510
633
550
457
343
319
–
– |
32,2
36,8
32,4
–
–
–
–
–
–
–
–
–
– |
280
320
57,7
–
–
–
–
–
–
–
–
–
– |
0,031
0,027
0,031
0,016
0,019
0,020
0,027
0,029
0,017
0,024
0,025
0,026
0,030 |
1,1
0,9
5,4
–
–
–
–
–
–
–
–
–
– |
1,0
0,9
2,7
–
–
–
–
–
–
–
–
–
– |
22,1
25,2
8,8
18,0
16,8
16,7
18,8
15,8
15,4
10,6
8,8
18,0
19,6 |
75
98
15
–
–
–
–
–
–
–
–
–
– |
203
254
81
272
221
212
195
158
223
119
106
–
– |
Примечание: U¥
= R×
c1 ×
c2 , fg = 1/c1 , a
f = 1/ c1 ×
c2 .
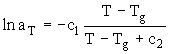 , (4) , (4)
где aT = t
(Т)/t
(Тg) @
h
(Т)/h
(Тg), c1 и c2 – эмпирические постоянные, которые в рамках теории флуктуационного свободного объема получают следующую трактовку
c1 @
1 / fg , (5)
c2 = a
f / fg . (6)
Здесь a
f = (df/dT)Tg – коэффициент теплового расширения флуктуационного свободного объема при температуре стеклования, равный скачку коэффициента объемного теплового расширения (КТР) при Tg (см. [1,2]): a
f = D
a
= (a
l – a
g), где a
l и a
g – КТР выше и ниже Tg (табл.1).
Уравнение ВЛФ фактически эквивалентно уравнению Фогеля–Фульчера–Таммана (ФФТ) (см. [2])
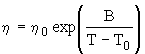 , (7) , (7)
причем эмпирические постоянные этих уравнений связаны между собой следующим образом
T0 = Tg – c2 , (8)
B = c1 ×
c2 , (9)
откуда с учетом соотношения (5) получаем возможность для расчета fg и a
f по данным о параметрах уравнения ФФТ:
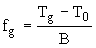 , (10) , (10)
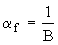 . (11) . (11)
Далее, располагая данными для fg, можно вычислять энергию образования флуктуационной дырки металлических стекол по формуле [2]
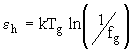 , (12) , (12)
где fg определяется из выражения (10).
С помощью соотношений (10)–(12) ниже проводится оценка fg , a
f , e
h и других величин для аморфных металлических сплавов.
Результаты расчета
Температурная зависимость вязкости аморфных сплавов в области стеклования описывается уравнением ФФТ, которое успешно используется практически для всех стеклующихся систем. В табл.2 приводятся значения параметров этого уравнения для ряда металлических стекол, заимствованные из книги Судзуки, Фудзимори и Хасимото [7], а в табл.3 – рассчитанные на их основе характеристики теории флуктуационного свободного объема этих стекол.
Обсуждение результатов
Как и следовало ожидать, доля флуктуационного свободного объема аморфных металлических сплавов, замороженная при температуре стеклования, оказывается практически постоянной величиной (табл.3) f g @
const »
0,025¸
0,027 и совпадает с данными для аморфных полимеров и силикатных стекол (табл.1).
Табл.2
Температуры плавления Tm, стеклования Tg и параметры уравнения
Фогеля–Фульчера–Таммана (7) для металлических стекол [7]
|
Аморфный сплав |
Tm , К |
Tg /Tm |
Tg , К |
h
0 ,
кПа×
с |
B, К |
T0 , К |
|
Ni
Ni62,4Nb37,6
Ni75Si8B17
Fe91B9
Fe89B11
Fe83B17
Fe41,5Ni41,5B17
Fe79Si10B11
Fe80P13C7
Pd82Si18
Pd77,5Cu6Si16,5
Pd40Ni40P20
Pt60Ni15P25
Te
Co75Si15B10
Ge |
1725
1442
1340
1628
1599
1448
1352
1419
1258
1071
1015
916
875
723
1393
1210 |
0,25
0,66
0,58
0,37
0,40
0,52
0,53
0,58
0,59
0,61
0,64
0,66
0,57
0,40
0,56
0,62 |
430
945
782
600
640
760
720
818
736
657
653
602
500
290
785
750 |
2,0
0,49
2,53
14,1
8,53
3,3
3,78
1,9
2,25
6,32
2,57
1,5
5,31
0,13
2,87
18,3 |
4700
5380
4280
4635
4625
4630
4500
4505
4600
3730
3820
3600
3560
3790
4190
1930 |
295
810
670
513
515
638
601
701
616
557
553
509
405
198
675
700 |
Табл.3
Параметры теории флуктуационного свободного объема для металлических стекол (использованы данные [7], см. табл.2)
|
Аморфный сплав |
с1 |
с2 , К |
fg |
a
f ×
105, К–1 |
e
h , |
U¥
, |
Ug , |
|
кДж/моль |
|
Ni
Ni62,4Nb37,6
Ni75Si8B17
Fe91B9
Fe89B11
Fe83B17
Fe41,5Ni41,5B17
Fe79Si10B11
Fe80P13C7
Pd82Si18
Pd77,5Cu6Si16,5
Pd40Ni40P20
Pt60Ni15P25
Te
Co75Si15B10
Ge |
34,8
39,9
38,2
53,3
37,0
38,0
37,8
38,5
38,3
37,3
38,2
38,7
37,5
41,2
38,1
38,6 |
135
135
112
87
125
122
119
117
120
100
100
93
95
92
110
50 |
0,029
0,025
0,026
0,019
0,027
0,026
0,026
0,026
0,026
0,027
0,026
0,026
0,027
0,024
0,026
0,026 |
21,28
18,59
23,36
21,57
21,62
21,60
22,22
22,20
21,74
26,81
26,18
27,78
28,09
26,39
23,87
51,81 |
12,7
28,9
23,7
19,8
19,2
23,0
21,7
24,8
22,3
19,8
19,8
18,3
15,1
9,0
23,7
22,8 |
39,1
44,7
35,6
38,5
38,4
38,5
37,4
37,4
38,2
31,0
31,7
29,9
29,6
31,5
34,8
16,0 |
124,4
313,0
248,3
265,6
196,8
239,7
226,3
261,7
234,5
203,6
207,3
193,6
155,7
99,3
248,5
240,6 |
Примечание: 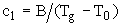 , , 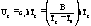
Таким образом, условие стеклования (1) применимо к металлическим стеклам.
В последнее время развито представление о том, что образование флуктуационной дырки в жидкостях и стеклах обусловлено предельным среднеквадратичным смещением кинетической единицы (атома, группы атомов) из равновесного положения, соответствующим максимуму силы межатомного взаимодействия [3,8]. Образование такой дырки объемом vh трактуется как локальное колебательное возбуждение структуры, а число флуктуационных дырок Nh – как число возбужденных кинетических единиц, ответственных за процесс стеклования. Линейный размер дырки vh1/3 характеризует критическое смещение частицы или, иначе, предельное удлинение межатомной связи D
rm.
Доля флуктуационного свободного объема fg зависит не только от объема дырки, но и от числа дырок в единице объема nh = Nh / V:
fg = vh ×
nh . (13)
Критическое смещение частицы vh1/3 и объемная концентрация возбужденных кинетических единиц nh у разных стеклообразных систем не обязательно должны быть одинаковы. Поэтому условие стеклования fg @
const выполняется лишь в первом приближении. Например, при росте К2О от 2,5 до 33,5 мол. % в калиевоборатных стеклах К2О–В2О3 число дырок в единице объема остается постоянным nh =23×
1026 м–3, а объем дырки vh падает с 14,8 до 10,9  , в результате чего величина fg снижается от 0,034 до 0,026 (табл.1). Уменьшение vh происходит из-за сшивающего действия ионов калия К+, обеспечивающих электронейтральность четырехкоординированного бора в группе , в результате чего величина fg снижается от 0,034 до 0,026 (табл.1). Уменьшение vh происходит из-за сшивающего действия ионов калия К+, обеспечивающих электронейтральность четырехкоординированного бора в группе 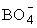 [3,8]. [3,8].
Как видно (табл.3), для аморфного сплава никеля имеем fg = 0,029, тогда как для системы никель–ниобий fg = 0,025. Можно предположить, что в этом сплаве ниобий создает сшивающий эффект, который снижает vh. Если в системе Fe91B9 величина fg принимает низкое значение 0,019, то в аморфных сплавах Fe89B11, Fe79Si10B11 и Fe80P13C7 она достигает “универсального” значения fg @
0,026. Следовательно, доля флуктуационного свободного объема fg в металлических стеклах, хотя и слабо, но зависит от их природы, как и в случае других стеклообразных систем [3,8].
Значение энергии образования флуктуационной дырки для аморфных сплавов e
h @
15¸
25 кДж/моль (табл.3), значительно ниже энергии активации вязкого течения и диффузионных процессов. Следовательно, образование флуктуационной дырки в этих системах представляет собой низкоэнергетический мелкомасштабный процесс, что согласуется с механизмом образования дырки в стеклообразных системах [3,8].
Зная значения e
h и коэффициента В в уравнении ФФТ, можно рассчитать температурную зависимость энергии активации вязкого течения металлических стекол по формуле дырочно-активационной теории [9]
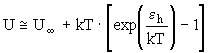 , (14) , (14)
где U¥
– энергия активации при Т®
¥
, которая определяется по данным о постоянной В. U¥
= k×
B.
Второе слагаемое в выражении (14) имеет смысл потенциала конфигурационного изменения структуры при элементарном акте вязкого течения, а величина U¥
– энергии активации перескока кинетической единицы в соседнюю (готовую) дырку [9].
По формуле [9]
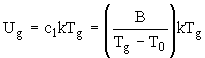
мы рассчитали энергию активации вязкого течения при температуре стеклования Ug=U(Tg) для исследованных металлических стекол. Значения Ug и U¥
приведены в табл.1 и 3.
Заключение
Доля флуктуационного свободного объема металлических стекол fg, замороженная при температуре стеклования, составляет fg @
0,026, что совпадает с данными о величине fg для органических аморфных полимеров и неорганических стекол. Образование флуктуационных дырок в аморфных сплавах представляет собой низкоэнергетический (e
h @
15¸
25 кДж/моль) мелкомасштабный процесс, как и у других стеклообразных систем.
Литература
- Ферри Дж. Вязкоупругие свойства полимеров. М.: ИЛ, 1963. 535с.
- Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 259с.
- Сандитов Д.С., Сангадиев С.Ш. Новый подход к интерпретации флуктуационного свободного объема аморфных полимеров и стекол // Высокомолек. соед. А. 1999. Т.41. №6. С.1-24.
- Френкель Я.И. Введение в теорию металлов. Л.-М.: ОГИЗ, 1948. 291с.
- Бетехтин В.И., Глезер А.М., Кадомцев А.Г., Кипяткова А.Ю. Избыточный свободный объем и механические свойства аморфных сплавов // Физика твердого тела. 1998. Т.40. №1. С.85-89.
- Глезер А.М., Молотилов Б.В. Структура и механические свойства аморфных сплавов. М.: Металлургия, 1992. 208с.
- Судзуки К., Фузимори Х., Хасимото К. Аморфные металлы. М.: Металлургия, 1987. 328с.
- Сандитов Д.С., Сангадиев С.Ш. Условие стеклования в теории флуктуационного свободного объема и критерий плавления Линдемана // Физ. и хим. стекла. 1998. Т.24. №4. С.417-428.
- Бартенев Г.М., Сандитов Д.С. Релаксационные процессы в стеклообразных системах. Новосибирск: Наука, 1986. 238с.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

