ОПИСАНИЕ КРИСТАЛЛИЧЕСКОГО СОСТОЯНИЯ ВЕЩЕСТВА НА ОСНОВЕ МЕТОДА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
Ю.В. Аграфонов, Т.В. Бирюлина
Иркутский Государственный Университет
Введение.
Одной из наиболее важных задач, стоящих в настоящее время перед современной физикой, является задача создания материалов с заданными свойствами, точного предсказания их поведения в определенных условиях, установления ресурса работы материалов и т. д. Это означает, что по известному потенциалу межмолекулярного взаимодействия, температуре и плотности системы частиц, необходимо уметь определять структуру и термодинамические свойства получаемого вещества. Такой подход реализуется в рамках статистической физики, где, исходя из общего уравнения статистической физики (уравнения Лиувилля) и на основе канонического распределения Гиббса, получен метод функций распределения комплексов частиц – бесконечная цепочка уравнений ББГКИ для частичных функций распределения. Эту зацепляющуюся систему уравнений можно преобразовать в систему всего двух точных интегральных уравнений, называемую обобщенным уравнением Орнштейна – Цернике для одно- и двухчастичной функции распределения, определяющих дальний и ближний порядок в веществе /1/:
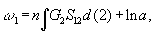 (1)
(1)
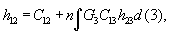 (2)
(2)
где n — плотность, 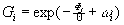 — одночастичная функция распределения, описывающая расположение i-ой частицы относительно лабораторной системы координат, w
i— одночастичный термический потенциал, учитывающий влияние окружения на данную частицу,
— одночастичная функция распределения, описывающая расположение i-ой частицы относительно лабораторной системы координат, w
i— одночастичный термический потенциал, учитывающий влияние окружения на данную частицу, 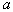 — коэффициент активности,
— коэффициент активности, 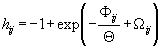 — парная корреляционная функция; двухчастичная функция распределения, Gij, описывающая взаимное расположение частиц друг относительно друга, связана с парной корреляционной функцией соотношением
— парная корреляционная функция; двухчастичная функция распределения, Gij, описывающая взаимное расположение частиц друг относительно друга, связана с парной корреляционной функцией соотношением 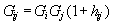 ; Фij— потенциальная энергия парного взаимодействия частиц i и j, находящихся на расстоянии rij=ç
ri – rjç
друг от друга, Фi — потенциальная энергия i-ой частицы во внешнем поле,
; Фij— потенциальная энергия парного взаимодействия частиц i и j, находящихся на расстоянии rij=ç
ri – rjç
друг от друга, Фi — потенциальная энергия i-ой частицы во внешнем поле, 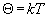 ,
, 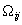 — двухчастичный термический потенциал, учитывающий опосредованное взаимодействие частиц через их окружение,
— двухчастичный термический потенциал, учитывающий опосредованное взаимодействие частиц через их окружение, 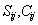 — прямые корреляционные функции:
— прямые корреляционные функции:
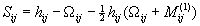 ,
, 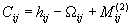 , (3)
, (3)
в которых 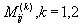 — бридж-функционалы, представляющие собой бесконечные ряды многосвязных диаграмм, которые аппроксимируют какими-либо простыми выражениями, называемыми уравнениями замыкания.
— бридж-функционалы, представляющие собой бесконечные ряды многосвязных диаграмм, которые аппроксимируют какими-либо простыми выражениями, называемыми уравнениями замыкания.
Система уравнений (1) – (2) является достаточно общей, благодаря чему с ее помощью можно описать все состояния вещества, включая фазовые переходы. Мы применим ее к описанию фазового перехода расплав – кристалл в двухкомпонентной системе и к описанию высокотемпературного однокомпонентного кристалла.
I. Кристаллизация двухкомпонентной системы.
Обобщим систему уравнений (1) – (2) на кристалл, состоящий из частиц двух сортов 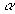 и
и 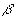 , с плотностями соответственно
, с плотностями соответственно 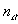 и
и 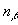 (полная плотность системы n=
(полная плотность системы n=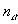 +
+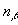 ). В этом случае его структура задается набором одночастичных функций распределения
). В этом случае его структура задается набором одночастичных функций распределения 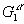 (r1),
(r1), 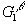 (r1), относящимся к отдельным частицам того или иного сорта, и набором двухчастичных функций распределения
(r1), относящимся к отдельным частицам того или иного сорта, и набором двухчастичных функций распределения 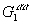 (r1, r2),
(r1, r2), 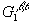 (r1, r2),
(r1, r2), 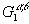 (r1, r2), относящимся к произвольной паре частиц того и другого сорта:
(r1, r2), относящимся к произвольной паре частиц того и другого сорта:
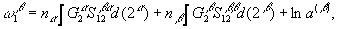 (4)
(4)
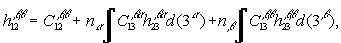 (5)
(5)
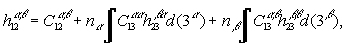 (6)
(6)
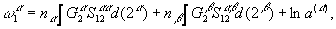 (7)
(7)
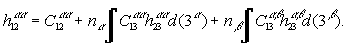 (8)
(8)
Совместное решение системы уравнений при заданных значениях парциальных плотностей 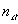 ,
,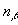 является сложной задачей. Однако в случае предельного разбавления, когда концентрация растворенного вещества
является сложной задачей. Однако в случае предельного разбавления, когда концентрация растворенного вещества 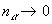 , а концентрация растворителя
, а концентрация растворителя 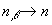 , система уравнений принимает более простой вид:
, система уравнений принимает более простой вид:
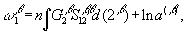 (9)
(9)
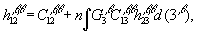 (10)
(10)
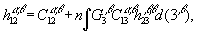 (11)
(11)
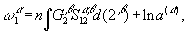 (12)
(12)
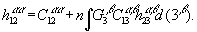 (13)
(13)
Первые два уравнения описывают однокомпонентную систему (чистый растворитель), решение для которой известно /2/. Уравнение (11) определяет парциальную корреляционную функцию растворенное – растворитель 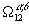 . Наконец, система (12) и (13), описывает корреляционные функции растворенного вещества
. Наконец, система (12) и (13), описывает корреляционные функции растворенного вещества 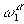 и
и 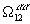 .
.
Используем подход, примененный для решения однокомпонентной системы /2/, к двухкомпонентному случаю.
Решение системы (9) – (13) можно искать в виде рядов по степеням малого параметра. В данном случае им не может быть ни температура, ни плотность, т. к. при кристаллизации они принимают большие значения. Поэтому в качестве параметра разложения выбирается малый параметр e, связанный со скачком плотности:
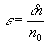 ,
, 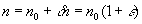 (14)
(14)
где n — плотность кристалла, n0 — плотность жидкости в точке еЈ кристаллизации.
Подставляя эти выражения в систему (9) – (13), получим в нулевом приближении уравнения для определения параметров жидкости на линии кристаллизации. На рис.1. приведены графики двухчастичных термических потенциалов W
bb
, W
a
b
и W
a
a
для системы твердых сфер и замыкания Мартынова – Саркисова для случая, когда частицы примеси в два раза меньше частиц растворителя.
Для описания собственно кристаллического состояния необходимо рассмотреть следующие порядки в разложении по e. Ограничиваясь первым порядком, приравняем соответствующие члены в разложении по 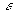 уравнений (9) — (13). Так как искомая структура кристалла имеет периодическую структуру, то ищутся периодические решения полученных уравнений в виде (индексы a и b опущены):
уравнений (9) — (13). Так как искомая структура кристалла имеет периодическую структуру, то ищутся периодические решения полученных уравнений в виде (индексы a и b опущены):
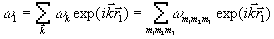 , (15)
, (15)
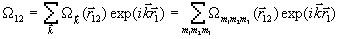 , (16)
, (16)
где 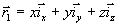 ,
, 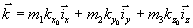 , а
, а 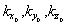 — основные периоды обратной решетки, m1, m2, m3 — любые целые положительные или отрицательные числа.
— основные периоды обратной решетки, m1, m2, m3 — любые целые положительные или отрицательные числа.
В первом случае, когда m1=m2=m3=0, получающиеся уравнения описывают кристалл на линии плавления. Графики функций 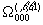 ,
, 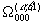 и
и 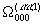 для замыкания Мартынова – Саркисова и потенциала твердых сфер для случая b>a приведены на рис. 2. В этом случае графики функций имеют сходство с аналогичными графиками для жидкости в точке плавления (рис. 1): все они имеют осциллирующий вид, максимумы и минимумы выражены больше у функции W
b
b
чем у W
a
b
, и у W
a
b
чем у W
a
a
, функция W
a
b
имеет локальный минимум вблизи нуля и при r»
6 все три функции практически равны нулю. Отличие проявляется в том, что в этом случае максимумы и минимумы функций более глубокие. В частности, функция W
b
b
имеет первый минимум порядка –50, а функция W
a
a
имеет необычный максимум при r»
5.
для замыкания Мартынова – Саркисова и потенциала твердых сфер для случая b>a приведены на рис. 2. В этом случае графики функций имеют сходство с аналогичными графиками для жидкости в точке плавления (рис. 1): все они имеют осциллирующий вид, максимумы и минимумы выражены больше у функции W
b
b
чем у W
a
b
, и у W
a
b
чем у W
a
a
, функция W
a
b
имеет локальный минимум вблизи нуля и при r»
6 все три функции практически равны нулю. Отличие проявляется в том, что в этом случае максимумы и минимумы функций более глубокие. В частности, функция W
b
b
имеет первый минимум порядка –50, а функция W
a
a
имеет необычный максимум при r»
5.
Во втором случае приравниваются члены при одинаковых комбинациях m1,m2,m3, а компоненты вектора 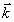 находятся из уравнения для однокомпонентной системы, сопоставляя каждому набору чисел m1,m2,m3 свою функцию
находятся из уравнения для однокомпонентной системы, сопоставляя каждому набору чисел m1,m2,m3 свою функцию 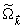 , которая ищется в виде рядов по полиномам Лежандра (индексы a и b опущены):
, которая ищется в виде рядов по полиномам Лежандра (индексы a и b опущены):
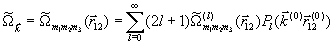 , (17)
, (17)
где 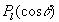 — полином Лежандра порядка l,
— полином Лежандра порядка l, 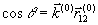 ,
, 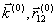 — единичные вектора, направленные вдоль
— единичные вектора, направленные вдоль 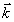 и
и 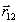 . Подставляя это выражение в разложение по e, получается система уравнений для одинаковых l, позволяющая определить функции
. Подставляя это выражение в разложение по e, получается система уравнений для одинаковых l, позволяющая определить функции 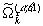 и
и 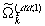 . Правда, получающиеся уравнения достаточно громоздки, и поэтому здесь не приводятся. Но они могут быть, как и в предыдущих случаях, решены численно.
. Правда, получающиеся уравнения достаточно громоздки, и поэтому здесь не приводятся. Но они могут быть, как и в предыдущих случаях, решены численно.
Таким образом, предложенная схема позволяет найти двухчастичный термический потенциал частиц разных сортов, и, зная его, все термодинамические функции получающегося вещества.
II. Высокотемпературный однокомпонентный кристалл.
Продолжим описание кристаллического состояния вещества. Для этого рассмотрим однокомпонентный кристалл, находящийся за линией кристаллизации. В этом случае его температура Т ниже, чем температура при кристаллизации ТК, поэтому вышеописанный подход здесь неприменим, т. к. в качестве начального приближения в нем выбираются термодинамические функции расплава, что неправомерно в данном случае. Поэтому для решения обобщенного уравнения Орнштейна—Цернике для высокотемпературного кристалла необходимо использовать несколько другой подход.
Так, в случае высокотемпературного кристалла мы уже имеем устойчивую структуру первого порядка. Т. к. она имеет периодический вид, будем искать решение системы (1) — (2) в классе периодических функций от радиуса-вектора частиц. Для этого представим решение в следующем виде:
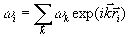 , (18)
, (18)
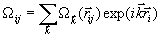 . (19)
. (19)
Подставляя данные ряды в систему (1) – (2), получим систему нелинейных уравнений относительно 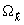 .
.
В первом порядке разложения по 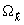 для ненулевых компонент (
для ненулевых компонент (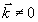 ) получим систему, которая представляет собой линейные интегральные уравнения и решается численно.
) получим систему, которая представляет собой линейные интегральные уравнения и решается численно.
Для нулевых компонент (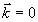 ) функцию
) функцию 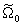 =const
=const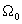 можно представить в виде разложения, нулевое приближение в котором равно
можно представить в виде разложения, нулевое приближение в котором равно 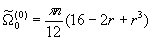 (0<r<2), и получить ее аналитическое выражение для потенциала твердых сфер. На интервале 0<r<1 она имеет вид в первом приближении:
(0<r<2), и получить ее аналитическое выражение для потенциала твердых сфер. На интервале 0<r<1 она имеет вид в первом приближении:
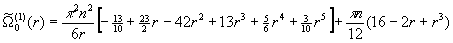 . (20)
. (20)
Для случая 1<r<2 она принимает вид:
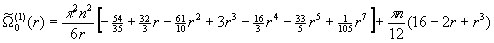 . (21)
. (21)
За этим интервалом (r>2) 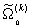 =0 благодаря входящим в выражение для ее определения функциям Майера fij(r).
=0 благодаря входящим в выражение для ее определения функциям Майера fij(r).
Таким образом, подставляя последовательно полученные выражения, можно получить аналитическое выражение функции 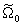 .
.
На рис. 3. представлено численное решение для функции 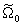 для системы твердых сфер и замыкания Мартынова – Саркисова. Решение приведено для трех значений плотностей: r=2.0, r=1.04 и r=0.5. Во всех трех случаях графики функции
для системы твердых сфер и замыкания Мартынова – Саркисова. Решение приведено для трех значений плотностей: r=2.0, r=1.04 и r=0.5. Во всех трех случаях графики функции 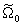 пропорциональны плотности и имеют подобный вид, монотонно спадая от максимального значения до нуля при r=2, что обусловлено видом выбранного потенциала. При первом значении плотности вещество находится в устойчивом кристаллическом состоянии. Второе значение плотности r=1.04 является плотностью плавления кристалла /3/. Последнее (r=0.5) – соответствует жидкой фазе. Вообще же говоря, решение в последнем случае не должно существовать, т. к. выбранный вид функций распределения не соответствует функциям распределения жидкости. При плотности же плавления данное решение должно также исчезать, соответствуя изменяющейся структуре вещества.
пропорциональны плотности и имеют подобный вид, монотонно спадая от максимального значения до нуля при r=2, что обусловлено видом выбранного потенциала. При первом значении плотности вещество находится в устойчивом кристаллическом состоянии. Второе значение плотности r=1.04 является плотностью плавления кристалла /3/. Последнее (r=0.5) – соответствует жидкой фазе. Вообще же говоря, решение в последнем случае не должно существовать, т. к. выбранный вид функций распределения не соответствует функциям распределения жидкости. При плотности же плавления данное решение должно также исчезать, соответствуя изменяющейся структуре вещества.
Описанное решение линейного приближения относится к области непосредственной близости к линии плавления кристалла. Если мы хотим получить решение при более низких температурах, то, в разложении необходимо учитывать следующие члены ряда по степеням 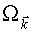 . Так, например, для уравнения во втором порядке по
. Так, например, для уравнения во втором порядке по 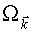 получается зацепляющаяся система уравнений, которая содержит фурье – компоненты, относящиеся к разным волновым векторам. Пренебрегая связью между этими фурье – компонентами (приближение хаотических фаз), можно получить систему линейных независимых уравнений с заданным значением волнового вектора, которые не приведены здесь из-за их громоздкости. Эти уравнения, также как и другие, можно решить численно.
получается зацепляющаяся система уравнений, которая содержит фурье – компоненты, относящиеся к разным волновым векторам. Пренебрегая связью между этими фурье – компонентами (приближение хаотических фаз), можно получить систему линейных независимых уравнений с заданным значением волнового вектора, которые не приведены здесь из-за их громоздкости. Эти уравнения, также как и другие, можно решить численно.
Таким образом, предложенный метод формально допускает решение поставленной задачи описания высокотемпературного кристалла. А для линейного приближения – даже возможность аналитического выражения для термических потенциалов.
Заключение.
Используя методы статистической физики предложено описание кристаллических веществ. Это описание кристаллизации двухкомпонентного расплава и описание высокотемпературного однокомпонентного кристалла.
В первом случае была рассмотрена система твердых сфер с частицами растворителя в два раза больших частиц примеси в случае предельного разбавления и с замыканием Мартынова – Саркисова. Для нее были получены выражения для термических потенциалов при разложении обобщенного уравнения Орнштейна – Цернике в ряды по степеням малого параметра, связанного со скачком плотности при кристаллизации. Для нулевого приближения получено численное решение, соответствующее жидкости в точке ее кристаллизации. Для первого приближения, т. е., собственно для кристаллического состояния, решение искалось в виде рядов Фурье и Лежандра. Для них были получены численные результаты в нулевом приближении, соответствующие кристаллу на линии плавления. Для следующего приближения получаются интегральные уравнения, которые могут быть также решены численно.
Для высокотемпературного кристалла рассматривалась также система твердых сфер и приближение Мартынова – Саркисова. В этом случае метод решения обобщенного уравнения Орнштейна – Цернике заключался в представлении входящих в него функций в периодическом виде. Для членов первого порядка разложения можно получить аналитическое решение, в частности, приведены выражения нулевого и первого приближения. Также приведено численное решение в линейном приближении для нескольких значений плотностей. Для квадратичного приближения, описывающего кристалл при более низких температурах, получаются интегральные уравнения, которые могут быть также численно решены.
Литература
- Мартынов Г. А. //ТМФ. 1975. Т. 22. № 1. С. 85-96.
- Аграфонов Ю. В., Мартынов Г. А. // ТМФ. 1992. т. 90. № 1. С. 113-127.
Аграфонов Ю.В. Физика конденсированного состояния вещества. Метод функций распределения: Учеб. пособие. — Иркутск: Иркут. ун-т, 1994.

