Некоторые аспекты учета поглощения лазерного излучения в оптоакустической томографии
А.А. Аливердиев
Институт физики Дагестанского Научного Центра РАН
Задача неразрушающей диагностики внутренней структуры непрозрачных объектов продолжает оставаться одной из актуальных проблем науки. В связи с этим в последние годы предлагаются и разрабатываются новые подходы к этому вопросу, в частности, связанные с привлечением пространства скоростей (импульсов) и времени. Таким образом, сформировались такие направления, как спектротомография [1-2], хронотомография [3], симплектическая томография [4], томография рассеивающих сред [5-6], оптоакустическая томография [7-11] и др.
В настоящей работе представлен наш подход к оптоакустической томографии, как к пространственно-временной томографии, использующей скорость распространения регистрируемого сигнала [10-14]. При этом решается задача аналитического учета поглощения лазерного излучения, в том числе при наличии дополнительного поглощения с отличным пространственным распределением. Приводятся результаты численных экспериментов, подтверждающих теоретические выводы.
Мы не будем здесь детально рассматривать природу оптоакустического взаимодействия. Это очень хорошо сделано в [8]. Кроме того, в отличие от [8], где для постановки прямой задачи использовался метод передаточной функции, нами предлагается более простой подход, где предполагается интегрирование интенсивности звука от всех возбужденных участков с учетом временной задержки, вызванной конечностью скорости звука. Так как рождение звука в разных участках независимо, подобная постановка задачи вполне адекватна. Кроме того, мы будем считать, что скорость звука в исследуемом объекте постоянна. Это в подавляющем большинстве случаев также оправдано. Таким образом, это позволяет включить оптоакустическую томографию в рамки хронотомографии [9], использующей скорость распространения регистрируемого сигнала..
Отметим, что линейное приближение в задаче оптоакустической томографии предполагалось как у нас, так и в [7-9]. В случае невозможности оного, усложнение в постановке и решении обратной задачи будут более чем значительны. [8, 15]. Итак, допустим имеется объект, в котором лазерный источник (расположенный в точке 0) вызывает оптоакустический отклик, который регистрируется внешним микрофоном. Так как лазерный луч можно сделать достаточно тонким, практически будем рассматривать пространственно одномерную задачу томографии.
Введем следующие обозначения
f(x) – нормированная функция распределения вторичного акустического источника;
T(t) – временной профиль лазерного импульса;
vs – скорость звука в исследуемом объекте;
a(x) – коэффициент поглощения инициирующего лазерного излучения в законе Бугера;
a0 – коэффициент суммарного поглощения то есть a0=ln(I/I0), где I0 - суммарная интенсивность инициирующего импульса, I - интенсивность импульса, прошедшего через объект. Отметим, что, так как возбуждение акустического сигнала идет за счет поглощения лазерного излучения, то можно предположить, что распределения a(x) и f(x) будут совпадать. Таким образом, можно положить a(x)=a0 f(x).
Для регистрируемой интегральной функции акустического излучения Gs(t) имеем
|
L
Gs(t) = ò
C f1(x) T(t-x/vs) dx
0 |
(1) |
где
|
x
C f1(x) = f(x) exp (-a0 т f(x)dx)
0 |
(2) |
где C - нормировочная константа, вводимая для того, чтобы для облегчения дальнейшего решения положить функции f(x) и f1(x) нормированными единице.
Уравнение (1) представляет собой уравнение Фредгольма I рода и может быть решено стандартными средствами. Если же длительность лазерного импульса Dt<<l/vs, то независимо от его формы функция T(t-x/vs) практически превращается в d-функцию и начинает выполняться равенство f1(x)=AGs((t-t0)/vs), где A - некоторая константа, t0 - время пика функции T(t). Таким образом, можно допустить, что с точностью до постоянного множителя известна функция C f1(x), где C=const, а сами функции f1(x) и f(x) нормированы к единице. Тогда для нахождения функции f(x) следует решить уравнение (2), где f1(x) и a0 - известны, С - не известна, а f(x) - требуется найти. Для этого введем функции
|
x x
F(x) = т f(x) dx и F1(x) = т f1(x) dx
0 0 |
(3) |
и будем полагать, что a0¹
0 (в противном случае решаемое уравнение обращается в тождество). В этом случае из (2) следует, что
|
C f1(x) = 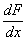 exp(-a0F) exp(-a0F) |
(4) |
Решая дифференциальное уравнение (4) для F и затем дифференцируя, получим окончательное решение
|
C f1(x)
f(x) = ¾
¾
¾
¾
¾
¾
1 - Ca0 F1(x) |
(5) |
Теперь из условий нормировки:
|
С = 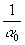 (1 - exp(-a0) ) (1 - exp(-a0) ) |
(6) |
Формулы (5)-(6) позволяют определить функцию f(x) из известной функции f1(x) при любом известном a0¹
0. При a0=0 в этом не было бы смысла, так как функция f1(x) была бы с точностью погрешности тождественна f(x).
Рассмотрим теперь случай, когда вместе с поглощением, связанным с оптоакустическим эффектом присутствует поглощение, имеющее иную природу. И пусть дифференциальный коэффициент этого поглощения равен a0'f'(x), где a0'=const, а f'(x) - нормированная известная функция.
|
x x
С f1(x) = f(x) exp(-a0 т f(x)dx - a0' т f '(x)dx)
0 0 |
(7) |
Введем функции
|
x
F '(x) = т f '(x) dx
0 |
(8) |
|
f1'= f1 exp(a0' F '(x) ) |
(9) |
|
x
F1'(x) = т f1(x) exp(a0' F '(x)) dx
0 |
(10) |
Аналогично предыдущему решению, получим
|
C f '1(x)
f(x) = ¾
¾
¾
¾
¾
¾
1 - Ca0 F '1(x) |
(11) |
Если теперь считать a0' и f '(x) известными, и нормировать f '1(x), то постоянную C можно вычислить по формуле (6). Функции f '1(x) и F '1(x) в этом случае полагаются известными, потому что они вычисляются из получаемой экспериментально функции f1(x) и положенных известными функции a0' и f '(x). Рассмотрим теперь вопрос, как определить a0' и f '(x). Коэффициент a0' может быть определен из абсолютного значения суммарной энергии принятого акустического сигнала (до сих пор эта величина нивелировалась нормировкой). Для этого скорее всего каждая конкретная установка должна быть проградуирована на эталонных образцах с различным соотношением a0 и a0'. Функция f '(x), в общем случае, не может быть известна. Однако, в ряде случаев она может быть характерной для данного исследуемого объекта. В частности, если дополнительное поглощение не зависит от координаты, она может быть тождественна константе l-1 Если же дополнительное поглощение пропорционально оптоакустическому, то, как видно из формулы (17), для решения задачи можно воспользоваться формулой (9), в которую вместо константы a0 следует подставить сумму a0+a0'.
|
|
|
|
a) |
b) |
|
|
|
|
c) |
d) |
|
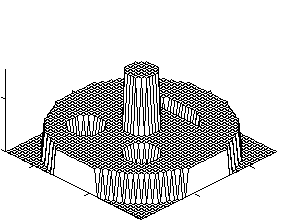
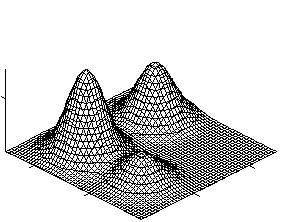
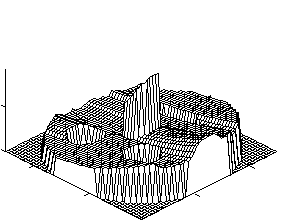
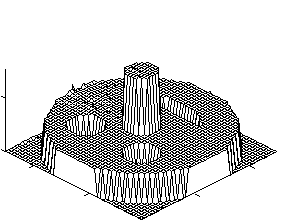
Рисунок 1. a) искомое распределение оптоакустической составляющей поглощения; b)распределение неоптоакустической составляющей поглощения; c) смоделированная функция оптоакустического отклика; восстановленная функция оптоакустического распределения. |
Следует отметить, что, так как звуковой сигнал передает только возбужденная часть исследуемого объекта, то мы можем поэтапно сканировать лазерным лучом по другим пространственным координатам. Таким образом, при каждом этапе сканирования возбуждается одна линия исследуемого объекта перпендикулярная торцам. В случае низкого взаимодействия вторичного акустического излучения с исследуемым объектом, измеренная торцевыми микрофонами временная развертка получаемого в результате лазерной накачки акустического импульса будет соответствовать исключительно этой возбужденной линии.
Нами был проведен ряд численных экспериментов. Для обеспечения максимальной наглядности и объективности результатов 1) предполагалось сканирование по дополнительной пространственной координате; 2) оптоакустическая и неоптоакустическая составляющие поглощения выбирались совершенно непохожими друг на друга. Характеристические данные экспериментов также выбирались типичными: линейные размеры образца l=0.1´
0.1 м2, длительность инициирующего лазерного импульса Dt=10-7с, скорость вторичной ультразвуковую волны vs=103 м/с. Зависимостью скорости от координаты пренебрегали. Типичные результаты представлены на рисунке. В данном случае полагали, что <a'(y)>=1,<a (y) >=1. При этом на функцию Gs(t) накладывали стохастический шум с относительной величиной 3%. Все представленные функции нормировали к единице.
Данные численных экспериментов полностью подтвердили теоретические выводы. Как видно из рисунков, даже при достаточно существенном внешнем шуме наблюдается хорошая восстанавливаемость искомой функции.
Работа была поддержана INTAS (Grant 96-0457) в рамках исследовательской программы ИЦ ФФМ.
Литература.
- Пикалов В.В., Преображенский Н.Г. Реконструктивная томография в газодинамике и физике плазмы. Новосибирск: Наука , 1987, 230с.
- Баландин А.Л., Преображенский Н.Г., Седельников А.Н. Томографическое определение трехмерного распределения частиц по скоростям // ПМТФ, 1989, N6 , с. 34-37.
- Левин Г.Г., Вишняков Г.Н. Оптическая томография. М: Радио и связь, 1989, 224 с.
- Man'ko O.V. Symplectic tomography of nonclassical states of a trapped ion, Preprint IC/96/39, ICTP, Trieste, 1996;
- S.R. Arridge, van der Zee, M. Cope, D.T. Deply, Reconstruction methods for infrared absorption imaging, proc. SPIE. 1990. 1431, pp.204-215.
- Fujimoto J.G., Brezinski M.E., Tearney G.J., Boppart S.A., Bouma B.E., Hee M.R., Southern J.F., and Swanson E.A. Biomedical imaging and optical biopsy using optical coherence tomography // Nature Medicine 1, 1995, p. 970-972.
- Карабутов А.А., Овчинников О.Б. // Судостроительная промышленность. Сер.“Акустика”, - Л.: ЦНИИ “РУМБ”, 1987, №2, с.725.
-
Гусев В.Э., Карабутов А.А. Лазерная оптоакустика, М.:“Наука”, 1991, 304с.
- A.A. Karabutov, N.B. Podymova, V.S. Letokhov // Time-resolved optoacoustic tomography of inchomogenus media. // Appl. Phys. B 63, 545-563, 1996.
- Каримов М.Г., Аливердиев А.А., О моделировании двумерного оптоакустического исследования возбужденных сред // Изв. ВУЗов Радиофизика, XLII, № 1, 1999, с. 83-86.
-
Аливердиев А.А., О возможности использования скорости регистрируемого сигнала для томографического исследования возбужденных сред // Изв. ВУЗов Радиофизика, XL, № 6, 1997, с. 761-768.
- Каримов М.Г., Аливердиев А.А. О реконструктивной задаче с учетом конечности скорости распространения несущего сигнала // Вестн. Моск. Ун-та, сер. 15, Вычисл. Матем. и Киберн. 1996, № 4, с. 55-56.
- Aliverdiev A.A., Karimov M.G. Solution of optic reconstructive problem considering registered signal velocity // Tr. J. of Physics, № 4, p.311-314, 1998
- Аливердиев А.А., Использование спектра скоростей для пространственно-временного исследования высокоскоростных процессов// ЖТФ, 1997, 67, № 9, с.132-134.
Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М.: Наука, 1975, 316 с.

