ДЫРОЧНО-КЛАСТЕРНАЯ МОДЕЛЬ И УНИВЕРСАЛЬНЫЕ СВОЙСТВА СТЕКЛООБРАЗНЫХ ТВЕРДЫХ ТЕЛ И ИХ РАСПЛАВОВ
Д.С. Сандитов, Ш.Б. Цыдыпов, Б.Д. Сандитов, С.Ш. Сангадиев
Бурятский государственный университет,
Введение
У стеклообразных систем (аморфных органических полимеров, неорганических стекол, аморфных сплавов – металлических стекол) обнаружены универсальные свойства. В акустической области спектра всех стекол наблюдаются дополнительные (в сравнении с кристаллами) квазилокальные низкоэнергетические колебательные возбуждения, которые приводят к аномальным низкотемпературным свойствам и к низкочастотному бозонному пику в КР–спектрах [1-5], причем все стекла ведут себя однотипно. Наряду с этим установлены универсальные правила и соотношения в области стеклования жидкостей [6,7]. Например, универсальной чертой релаксационных процессов в области стеклования является их неэкспоненциальность, в частности существование универсального дробно- экспоненциального закона Кольрауша [8]. У различных по природе стекол при 200С наблюдается эффект пластичности [6,9-11].
Очевидно, эти универсальные свойства обусловлены определенными общими динамическими закономерностями в стеклообразных веществах, хотя по морфологиям структур они различны. За последние годы появились модели кинетических явлений в стеклах и их расплавах, которые обладают достаточной универсальностью и не опираются на конкретную химическую природу этих систем. Они основаны на некоторых базовых принципах, позволяющих учесть эффекты кооперативности и неоднородности структуры стеклообразующих систем [1-5, 8-14].
На роль одного из таких общих феноменологических подходов может претендовать дырочная теория в варианте дырочно-кластерной модели [1,2,9,15]. Во-первых, в ее рамках находят наиболее естественную трактовку универсальные правила и уравнения в области стеклования жидкостей (правило Симха–Бойера, уравнение Вильямса–Ландела–Ферри и т. д.) [6,7]. Во-вторых, с помощью дырочно-кластерной модели успешно объясняются низкотемпературные аномалии тепловых и акустических свойств стекол [1]. В-третьих, прослеживается тесная связь между параметрами данной модели и характеристиками низкочастотного бозонного пика в КР–спектрах [16]. И, наконец, в рамках дырочно-кластерной модели вполне удовлетворительно описываются основные закономерности пластической деформации стеклообразных твердых тел [9-11]. Целью настоящей работы являются краткий обзор и анализ дырочно-кластерной модели стекол и их расплавов.
Дырочно-кластерная модель
Как стеклообразное твердое тело, так и его расплав рассматриваются как микронеоднородная среда, состоящая из двух динамических компонентов: упорядоченных областей (кластеров), расположенных в неупорядоченной среде (рыхлоупакованной матрице). При внешнем воздействии кластеры испытывают перестройку, что выражается в диффузионном обмене флуктуационными дырками –возбужденными кинетическими единицами между этими компонентами: кластерами и рыхлоупакованной матрицей [1,2,9,15]. Флуктуационный свободный объем сосредоточен в рыхлоупакованной матрице в виде дырок. Отрыв кинетической единицы (атома, группы атомов) от кластера в результате тепловых флуктуаций или под внешним воздействием означает образование дырки, а присоединение кинетической единицы к кластеру – как схлопывание дырки. Размягчение стекла при нагревании объясняется распадом кластеров. Элементарный акт этого процесса сводится к отрыву от кластера кинетической единицы, ответственной за стеклование жидкостей. Он описывается как образование флуктуационной дырки критического минимального объема vh , линейный размер которой соответствует предельному растяжению межатомной связи.
Таким образом, образование флуктуационной дырки объемом vh обусловлено флуктуационным отклонением расстояния между соседними кинетическими единицами от среднего значения r0 , соответствующим максимуму силы межатомного взаимодействия Fm [17]
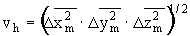 ,
,
где 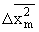 ,
, 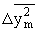 ,
, 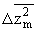 – критические среднеквадратичные смещения кинетической единицы по соответствующим осям.
– критические среднеквадратичные смещения кинетической единицы по соответствующим осям.
Образование такой дырки мы рассматриваем как локальное колебательное возбуждение, а число дырок Nh – как число возбужденных кинетических единиц, ответственных за ряд явлений, в частности за процесс стеклования. Умножив vh на число дырок Nh = Nh(T,P), получаем флуктуационный свободный объем системы: Vf = vh ×
Nh.
Критические флуктуационные растяжения межатомной связи представляют собой редкие флуктуации, особенно при низких температурах. Поэтому доля флуктуационного свободного объема стеклообразных веществ при температуре стеклования составляет всего 2¸
3 % от общего объема системы [6]:
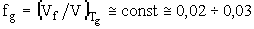 .
.
Величина f = Vf / V является функцией среднего квадрата относительной флуктуации плотности возбужденных кинетических единиц [6, c.118]:
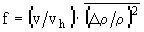 .
.
При 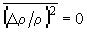 имеем f=0, хотя классический вандерваальсовский свободный объем отличен от нуля. В соотношении Vf = V – V0 занятый объем V0 имеет смысл объема системы в отсутствии флуктуации плотности возбужденных кинетических единиц.
имеем f=0, хотя классический вандерваальсовский свободный объем отличен от нуля. В соотношении Vf = V – V0 занятый объем V0 имеет смысл объема системы в отсутствии флуктуации плотности возбужденных кинетических единиц.
В рамках развиваемых представлений относительное число дырок Nh /N, а также доля флуктуационного свободного объема жидкостей и стекол
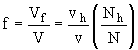 ,
,
где v=V/N - объем, приходящийся на частицу (v»
vh), в уравнении Френкеля выражают вероятность перехода кинетической единицы в возбужденное состояние или, иными словами, вероятность ее критического смещения [6]:
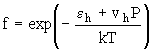 . (1)
. (1)
Энергия образования дырки равна работе смещения частицы
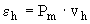 , (2)
, (2)
совершаемой против максимального внутреннего давления 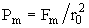 , обусловленного силами взаимодействия между атомами. При обычных давлениях порядка Р»
105 Pa, как правило, e
h >
>
vh ×
P , поэтому энтальпия образования дырки Hh = e
h + vh ×
P совпадает с величиной e
h . Отсюда из (1) получаем формулу для расчета e
h при T=Tg и f=fg :
, обусловленного силами взаимодействия между атомами. При обычных давлениях порядка Р»
105 Pa, как правило, e
h >
>
vh ×
P , поэтому энтальпия образования дырки Hh = e
h + vh ×
P совпадает с величиной e
h . Отсюда из (1) получаем формулу для расчета e
h при T=Tg и f=fg :
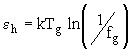 . (3)
. (3)
Из уравнения состояния (1) и термодинамического определения изотермического модуля объемного сжатия 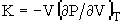 ранее одним из авторов было получено простое соотношение для расчета объема флуктуационной дырки при T=Tg (см.[6]):
ранее одним из авторов было получено простое соотношение для расчета объема флуктуационной дырки при T=Tg (см.[6]):
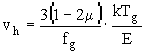 , (4)
, (4)
где Е=3(1-2m
)К – модуль упругости при одноосной деформации, m
- коэффициент Пуассона.
Для стеклообразных органических полимеров объем дырки составляет 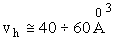 , что заметно ниже объема сегмента. Энергия образования дырки e
h @
10¸
13 кДж/моль близка к энергии межмолекулярного взаимодействия. Образование флуктуационной дырки в них обусловлено предельной деформацией межмолекулярных связей между участками – звеньями цепных макромолекул. У щелочносиликатных стекол параметры модели составляют
, что заметно ниже объема сегмента. Энергия образования дырки e
h @
10¸
13 кДж/моль близка к энергии межмолекулярного взаимодействия. Образование флуктуационной дырки в них обусловлено предельной деформацией межмолекулярных связей между участками – звеньями цепных макромолекул. У щелочносиликатных стекол параметры модели составляют 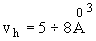 и e
h @
13¸
15 кДж/моль. Образование дырки в этих стеклах связанно с предельным смещением мостикового иона кислорода.
и e
h @
13¸
15 кДж/моль. Образование дырки в этих стеклах связанно с предельным смещением мостикового иона кислорода.
Таким образом, образование и схлопывание флуктуационных дырок в аморфных полимерах и неорганических стеклах представляют собой мелкомасштабные низкоэнергетические процессы, что согласуется с предлагаемым механизмом образования дырки.
В последние годы методом аннигиляции позитронов проведены измерения количества, размеров и относительного содержания дырок свободного объема в различных полимерах [20,21]. Согласно позитронно-аннигиляционной спектрометрии [20], позитроний – связанная система позитрон-электрон стремится локализоваться до аннигиляции в дырках свободного объема. Например, для параметров теории флуктуационного свободного объема vh , fg и nh = fg / vh получены следующие значения: у эпоксидного аморфного полимера vh = 62 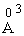 и fg =0,029 [21], у политриметилсилилпропина nh »
1025 м--3 [20,21], которые по порядку величин находятся в согласии с результатами нашего расчета [7,17,22,]. По-видимому, позитрон и позитроний локализуются в тех микрообластях, где имеет место предельная деформация межмолекулярных связей (флуктуационные дырки).
и fg =0,029 [21], у политриметилсилилпропина nh »
1025 м--3 [20,21], которые по порядку величин находятся в согласии с результатами нашего расчета [7,17,22,]. По-видимому, позитрон и позитроний локализуются в тех микрообластях, где имеет место предельная деформация межмолекулярных связей (флуктуационные дырки).
Обсуждение результатов
В рамках нового подхода к интерпретации механизма образования дырки флуктуационный свободный объем жидкостей и стекол в принципе может меняться с изменением температуры при постоянном объеме системы. Кажущееся противоречие между температурной зависимостью вязкости при V=const и теорией свободного объема является следствием ошибочной трактовки свободного объема в уравнении вязкости как классического вандерваальсовского свободного объема, который не меняется при V=const.
Можно устранить расхождение между расчетом величины (dTg/dP) и экспериментальными данными, если в дырочно-кластерную модель ввести поправку, учитывающую изменение структуры полимера под действием внешнего давления в области стеклования [17]. Аналогичным образом снимается противоречие между опытом и расчетом предела текучести аморфных полимеров [9]. Новый подход к механизму образования флуктуационной дырки позволяет установить количественную связь между условием стеклования жидкости и критерием плавления Линдемана [17,22]. Обратимся к теории гармонического осциллятора. Известно, что средняя кинетическая энергия осциллятора (kT/2) равна его средней потенциальной энергии ( ), откуда
), откуда 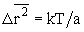 , где а – коэффициент квазиупругой силы, который непосредственно выражается через модуль упругости E=a/r0. Следовательно, среднеквадратичное смещение атома равно отношению
, где а – коэффициент квазиупругой силы, который непосредственно выражается через модуль упругости E=a/r0. Следовательно, среднеквадратичное смещение атома равно отношению
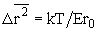 .
.  (5)
(5)
Принимая во внимание представление о том [6,17], что при температуре размягчения T=Tg среднеквадратичное смещение атома принимает предельное значение 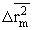 , множитель kTg /E в формуле (5) можно представить в виде
, множитель kTg /E в формуле (5) можно представить в виде
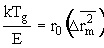 . (6)
. (6)
Легко убедиться, что комбинация соотношений (4) и (6) дает возможность выразить условие стеклования fg »
const через критерий плавления  :
:
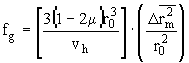 . (7)
. (7)
Полагая vh »
r03 [21] и m
»
0,25 , получаем следующую приближенную формулу
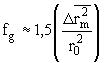 , (8)
, (8)
которая находится в согласии с экспериментальными данными: fg »
0,015¸
0,030 и d
2 »
0,01¸
0,02.
Эти результаты согласуются с расчетом амплитуды среднеквадратичных тепловых смещений атомов стекла с учетом избыточной плотности низкоэнергетических колебательных возбуждений, которая примерно в 1,5 раза больше, чем при той же температуре в кристаллической фазе [3,4]. В самом деле, отношение fg1/3 /d
имеет такой же порядок величины, что и указанная оценка (~
1,5). Поэтому, квазирешетка стекла должна размягчаться при более низкой температуре Tg, чем температура плавления решетки кристалла Ts . С этих позиций можно обосновать известное эмпирическое правило “двух третей” для соотношения между температурами стеклования и плавления [4]: Tg / Ts »
2/3.
Отметим, что классический вандерваальсовский свободный объем VF =(V-b), рассчитанный по плотности упаковки атомов и представляющий собой пустое пространство между ними, у стекол составляет около 25¸
30% от объема системы (VF / V »
0,3), т.е. на порядок выше доли флуктуационного свободного объема fg @
0.02¸
0.03 [6].
Заключение
Таким образом, механизм образования флуктуационной дырки, основанный на представлении о критическом среднеквадратичном смещении кинетической единицы, позволяет снять часть противоречий между теорией свободного объема и рядом экспериментальных данных, а также оказывается полезным при анализе ряда других явлений в стеклообразных системах, в частности при анализе универсальных свойств этих веществ.
Эти вопросы подробно обсуждаются в обзорной статье [17], а также в других публикациях [9,15,22,23].
Литература
- Чабан И.А. Микроскопическая модель низкотемпературных аномалий в диэлектрических стеклах//Физика твердого тела. 1979.Т.21.№5.с.1444-1450
-
Исакович М.А., Чабан И.А. Распространение волн в сильновязких жидкостях // Журн. экспер. и теорет. физики. 1966. Т.50. №5. С.1343-1362.
-
Малиновский В.К., Новиков В.Н., Соколов А.П. Особенности динамики и пространственных корреляций в генезисе стеклообразного состояния // Физ. и хим. стекла. 1996. Т.22. №3. С.204-221.
- Новиков В.Н. Наноструктура и низкоэнергетические колебательные возбуждения в стеклообразных материалах. Автореф. докт. дисс. Новосибирск: Институт автоматики и электрометрии СО РАН, 1992. 37с.
- Соколов А.П. Спектроскопия низкочастотного комбинационного рассеяния света в неупорядоченных материалах. Автореф. докт. дисс. Новосибирск: Институт автоматики и электрометрии СО РАН, 1993. 36с.
- Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. 259с.
- Козлов Г.В., Сандитов Д.С. Ангармонические эффекты и физико-механические свойства полимеров. Новосибирск: Наука, 1994. 260с.
- Волчек А.О., Гусаров А.И., Доценко А.В. Механизмы возникновения неэкпоненциальности релаксации в области стеклования // Физ. и хим. стекла. 1996. Т.22. №4. С.417-425.
-
Сандитов Д.С., Козлов Г.В., Сандитов Б.Д. Дырочно-кластерная модель пластической деформации стеклообразных твердых тел // Физ. и хим. стекла. 1996. Т.22. №6. С.683-693.
-
Бетехтин В.И., Глезер А.М., Кадомцев А.Г., Кипяткова А.Ю. Избыточный свободный объем и механические свойства аморфных сплавов // Физика твердого тела. 1998. Т.40. №1. С.85-89.
- Глезер А.М., Молотилов Б.В. Структура и механические свойства аморфных сплавов. М.: Металлургия, 1992. 208с.
- Ngai K.L., Rajagopal A.K., Teiller S. Slonring down of relaxation in a complex system by constraint dynamics // J. Chem. Phys. 1988. V.88. N8. P.5086-5094.
- Palmer R.G., Stein D.L., Abraham’s E., Anderson P.W. Models to hierarchically constrains dynamics for glassy relaxation//Phys. Rev. Lett. 1984.V.53.р.958-961
-
Маломуж Н.П., Шапиро М.М. Особенности кластеризации молекул в вязких жидкостях // Журн. физ. химии. 1997. Т.71. №3. С.468-474.
-
Сандитов Д.С., Козлов Г.В., Белоусов В.Н., Липатов Ю.С. Кластерная модель и модель флуктуационного свободного объема полимерных стекол // Физ. и хим. стекла. 1994. Т.20. №1. С.3-12.
-
Сандитов Д.С. Ангармонизм колебаний квазирешетки и модель флуктуационных дырок в стеклообразных твердых телах и их расплавах // Физ. и хим. стекла. 1991. Т.17. №4. С.525-534.
-
Сандитов Д.С., Сангадиев С.Ш. Новый подход к интерпретации флуктуационного свободного объема аморфных полимеров и стекол // Высокомолек. соед. А. 1999. Т.41. №6. С.1-23.
- Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975. 424с.
- Lindemann F.A. Uber die Berechnung molecularer Eiqenfrequenter // Phys. Zs. 1910. Bd.11. S.609-618.
- Wang Y.Y., Nakanishi H., Jean Y.C., Sandareski T.C. Positron annihilation in amino-cured epoxy polymers-pressure dependence // J. Polym. Sci. Part B. 1990. V.28. №9. P.1431-1441.
-
Deng Q., Sunder C.S., Jean Y.C. Pressure dependence of free-volume hole properties in an epoxy polymer // J. Phys. Chem. 1992. V.96. №1. P.492-495.
- Сандитов Д.С., Сангадиев С.Ш. Условие стеклования в теории флуктуационного свободного объема и критерий плавления Линдемана // Физ. и хим. стекла. 1998. Т.24. №4. С.417-428.
Сандитов Д.С., Сангадиев С.Ш. Коэффициент Пуассона и флуктуационный свободный объем аморфных полимеров и стекол // Высокомолек. соед. А. 1998. Т.40. №12. С.1-8.

