РАСЧЕТ СПЕКТРАЛЬНЫХ РЕШЕТОК
Л.Л. Досколович
Институт систем обработки изображений РАН,
Введение
Разработан метод расчета спектральных фазовых дифракционные решеток для разделения трех длин волн по трем различным дифракционным порядкам. Метод применен к расчету двухволновых дифракционных оптических элементов, предназначенных для разделения и заданного преобразования двух спектральных компонент освещающего пучка.
Расчету и использованию дифракционных оптических элементов (ДОЭ) для преобразования и фокусировки монохроматического излучения посвящено большое количество работ. Для работы с различными длинами волн известны спектральные дифракционные решетки (color separation gratings), позволяющие разделить три длины волны
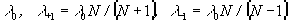 , (1)
, (1)
где N – целое число, по 0, +1 и -1 дифракционным порядкам [1-3]. Спектральные решетки имеют множество потенциальных применений в таких областях как спектроскопия, цветная печать и фотографии, распознавание и формирование цветных изображений [1-3]. Перспективным является использование спектральных решеток для селективного возбуждения и разделения продольных мод для повышения пропускной способности волоконно-оптических линий связи.
В данной статье рассмотрен расчет спектральных решеток, обобщающих известные решетки на случай более общей связи длин волн и номеров дифракционных порядков. Метод расчета решеток применен к расчету ДОЭ, предназначенных для выполнения двух различных оптических функций для двух длин волн.
Рассмотрим сначала известные спектральные дифракционные решетки, позволяющие разделить длины волн (1) по 0, +1 и -1 дифракционным порядкам. Спектральная решетка имеет на периоде N ступенек равной ширины с высотой [1-3]
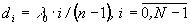 (2)
(2)
где n- показатель преломления материала решетки для длины волны l0. Пренебрегая дисперсией материала решетки, определим связь фазового набега j с высотой рельефа решетки для длины волны 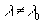 в виде [1-3];
в виде [1-3];
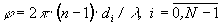 (3)
(3)
Согласно (3) получим, что решетка (2) для плоских пучков с длинами волн (1) формирует следующие фазовые набеги;
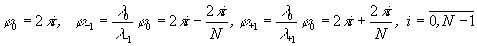 (4)
(4)
С учетом 2p-периодичности фазы, представим фазовые набеги (4) в виде:
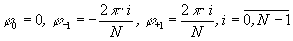 (5)
(5)
Поскольку для длины волны l0 фазовый набег равен нулю, то данная спектральная компонента направляется в нулевой порядок. Для длин волн l±1 фазовые набеги (5) соответствуют фазовым функциям призм, квантованных по N уровням;

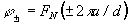 (6)
(6)
где d –период решетки, а функция
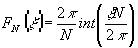 (7)
(7)
описывает операцию квантования по N уровням. Это обеспечивает фокусировку длин волн l±1 в порядках ±1. Вследствие квантования, доля энергии спектральных компонент l±1 фокусируемая в порядках ±1, описывается функцией;
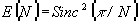 . (8)
. (8)
Рассмотрим расчет спектральных решеток, обобщающих известные решетки (2). Дисперсию материала решетки учитывать не будем [1-3]. Первоначально проведем расчет решетки для разделения по двум порядкам с номерами n0 и n1 длин волн l0, l1, связанных более общим по сравнению с уравнением (1) соотношением
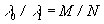 (9)
(9)
где M и N - взаимно-простые числа. Профиль такой решетки предлагается определить через фазовые функции квантованных по M и N уровням дифракционных призм

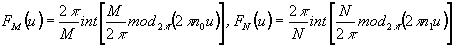 (10)
(10)
где 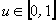 - координата профиля, нормированная на период решетки. Для удобства выкладок рельеф спектральной решетки определим через индексы значений
- координата профиля, нормированная на период решетки. Для удобства выкладок рельеф спектральной решетки определим через индексы значений 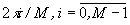 ,
, 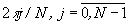 , принимаемых квантованными функциями
, принимаемых квантованными функциями 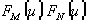 , в виде;
, в виде;
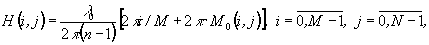 (11)
(11)
где M0(i,j) - неизвестная функция, принимающая целые неотрицательные значения. Решетка (11) при l=l0 формирует фазовый набег равный по модулю 2p фазовой функции квантованной призмы 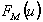 . Это обеспечивает фокусировку длины волны l0 в порядке n0. При l=l1 фазовый набег, формируемый решеткой (11), имеет вид
. Это обеспечивает фокусировку длины волны l0 в порядке n0. При l=l1 фазовый набег, формируемый решеткой (11), имеет вид
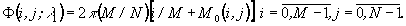 (12)
(12)
Для фокусировки компоненты l1 в порядке n1 функция M0(i,j) в (11) должна выбираться из условия равенства по модулю 2p выражения (12) квантованной фазе 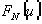 в (10). Это дает для расчета функции M0(i,j) следующее уравнение
в (10). Это дает для расчета функции M0(i,j) следующее уравнение
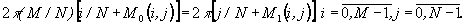 (13)
(13)
где M1(i,j) - произвольная функция, принимающая целочисленные значения. При прямой подстановке - решение уравнения (13) имеет вид:
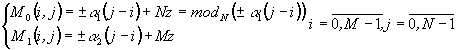 , (14)
, (14)
где a1, a2 - целые числа, определяемые из решения уравнения
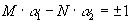 . (15)
. (15)
Поскольку числа M и N взаимно-простые, то уравнение (15) всегда имеет решение в целых числах по теореме о наибольшем общем делителе. Согласно (14), формула для профиля спектральной решетки имеет вид:
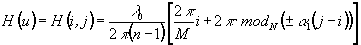 , (16)
, (16)
где 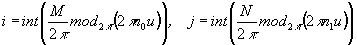 . Частным случаем (16) является решетка
. Частным случаем (16) является решетка
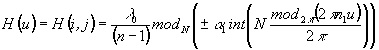 (17)
(17)
для разделения спектральных компонент
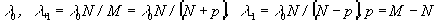 (18)
(18)
по порядкам 0, и +n1 и -n1. В частности, из (17) несложно получить, что спектральная решетка для разделения длин волн (18) по порядкам 0 и ±1 имеет на периоде N ступенек равной ширины с высотой
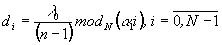 (19)
(19)
где a1 определяется из решения уравнения (15). Известные спектральные решетки [1-3] являются частным случаем решетки (19) при M=N+1.
Уравнения (11), (16) могут быть использованы для расчета двухволновых дифракционных оптических элементов (ДОЭ), предназначенных для разделения и преобразования двух длин волн из (18). Обозначим 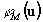 ,
, 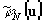 квантованные по M и N уровням фазовые функции, рассчитанные для некоторых заданных преобразований плоских монохроматических пучков с длинами волн l0, l+1 из (18). Тогда высота рельефа в каждой точке u апертуры двухволнового ДОЭ определяется по формулам (14)-(16), где числа (i,j) соответствуют индексам значений квантованных функций
квантованные по M и N уровням фазовые функции, рассчитанные для некоторых заданных преобразований плоских монохроматических пучков с длинами волн l0, l+1 из (18). Тогда высота рельефа в каждой точке u апертуры двухволнового ДОЭ определяется по формулам (14)-(16), где числа (i,j) соответствуют индексам значений квантованных функций 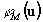 ,
, 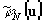 в данной точке. Таким образом, расчет двухволнового ДОЭ сводится к двум независимым задачам расчета квантованных фазовых функций, для решения которых разработаны эффективные итерационные алгоритмы [4, 5]. В качестве примера рассмотрим расчет ‘двухволновых решеток’ для формирования 4-х порядков ±2, ±1 при длине волны l=l0 и 3-х порядков 0, ±1 при длинах волн l+1=3l0/4 и l+1=9l0/4, соответственно. Расчет решеток (период d) проведем по формуле (16) на основе квантованных фазовых функций 4-х и 3-порядковой решеток, принимающих в интервалах периода
в данной точке. Таким образом, расчет двухволнового ДОЭ сводится к двум независимым задачам расчета квантованных фазовых функций, для решения которых разработаны эффективные итерационные алгоритмы [4, 5]. В качестве примера рассмотрим расчет ‘двухволновых решеток’ для формирования 4-х порядков ±2, ±1 при длине волны l=l0 и 3-х порядков 0, ±1 при длинах волн l+1=3l0/4 и l+1=9l0/4, соответственно. Расчет решеток (период d) проведем по формуле (16) на основе квантованных фазовых функций 4-х и 3-порядковой решеток, принимающих в интервалах периода 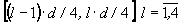 значения (0, p, p/2, 3p/2) и (0, 0, 2p/3, 2p/3), соответственно. В скалярном приближении Кирхгофа интенсивности порядков Ij для решетки с фазой
значения (0, p, p/2, 3p/2) и (0, 0, 2p/3, 2p/3), соответственно. В скалярном приближении Кирхгофа интенсивности порядков Ij для решетки с фазой 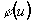 определяются как квадраты модулей коэффициентов Фурье функции
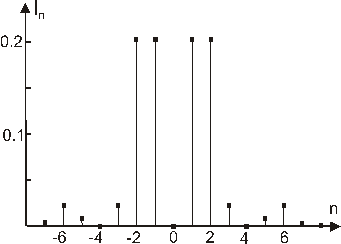
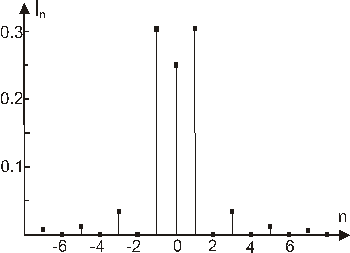
определяются как квадраты модулей коэффициентов Фурье функции 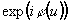 . Для 4-порядковой решетки I-2=I-1=I1=I-2=0.205, а для 3-порядковой решетки I0=0.304, I-1=I1==0.25. Следовательно, приведенные решетки концентрируют более 80% энергии в требуемых порядках -2, -1, +1, +2 и -1, 0, +1. При l+1=3l0/4 из (14)-(16) получим a1=a2=1 и
. Для 4-порядковой решетки I-2=I-1=I1=I-2=0.205, а для 3-порядковой решетки I0=0.304, I-1=I1==0.25. Следовательно, приведенные решетки концентрируют более 80% энергии в требуемых порядках -2, -1, +1, +2 и -1, 0, +1. При l+1=3l0/4 из (14)-(16) получим a1=a2=1 и 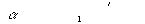 . При этом рельеф спектральной решетки для длин волн l0 и l+1=3l0/4 принимает вид:
. При этом рельеф спектральной решетки для длин волн l0 и l+1=3l0/4 принимает вид:
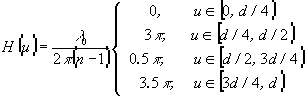 (20)
(20)
|
|
|
|
а) |
б) |
|
Рис.1. Интенсивности порядков решеток (20) и (21) для длин волн l0 (а) и l+1=9l0/4 (б). |
При l+1=9l0/4 из (14)-(16) получим a1=-2, a2=1, 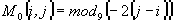 . В результате рельеф двухволновой решетки для длин волн l0 и l+1=9l0/4 принимает вид:
. В результате рельеф двухволновой решетки для длин волн l0 и l+1=9l0/4 принимает вид:
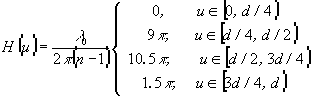 (21)
(21)
Интенсивности дифракционных порядков решеток (20) и (21) при освещающих пучках с длинами волн l0, l+1=3l0/4 и l0, l+1=9l0/4 совпадают (рис.1). Рис. 1 показывает независимое формирование 4-х и 3-х порядков для двух различных волн, что подтверждает работоспособность предложенного метода расчета.
Литература
- H. Dammann. Color separation gratings//Appl.Opt.,1978,v.17,N.15,p.2273-2279.
- H. Dammann. Spectral Characteristics of Stepped-phase Gratings//Optic, 1979, v.53, pp. 409-417.
- M. W. Farn, M. B. Stern. Color separation by use of binary optics//Opt.Lett., 1993, v.18, pp. 1214-1216.
- L.L. Doskolovich, P. Perlo, O.I. Petrova, P. Repetto, V.A. Soifer. Direct 2D calculation of quantized DOEs on the basis of a continuous series approach//Jour. of Mod.Opt., 1997, v. 44, pp.685-695.
L.L. Doskolovich, P. Perlo, O.I. Petrova, P. Repetto, V.A. Soifer. Direct two-dimensional calculation of binary DOEs using a non-binary series expression approach//Int. Jour. Of Optoelectronics, 1995, v. 10, pp.243-249.

