ТЛЕЮЩИЙ РАЗРЯД В ВИХРЕВОМ ПОТОКЕ ГАЗА

Х.Д. Ламажапов, В.Т. Волов, А.Д. Марголин, В.М. Шмелев

Институт инженеров транспорта

Тлеющий разряд характеризуется высокой степенью неравновесности, сильным отрывом электронных, а в случае разряда в молекулярных газах, и колебательных температур от газовой. Это позволяет использовать тлеющий разряд для накачки активных сред газовых лазеров [1], для работы плазмохимических реакторов [2], для обработки металлических поверхностей [3]. Для повышения эффективности и производительности этих устройств необходимо повышение плотности тока, повышение плотности газовой среды и скорости газового потока. Но при увеличении плотности тока тлеющий разряд скачкообразно переходит из объемно-однородного состояния в неоднородное. Это явление называется шнурованием. При шнуровании почти весь ток концентрируется в одном или нескольких каналах - шнурах, замыкающих газоразрядный промежуток. Состояние плазмы в токовых шнурах приближается к равновесному, что делает ее непригодным для использования в этих устройствах. Причем с повышением давления газовой смеси порог шнурования снижается, и для многих способов применения тлеющего разряда шнурование является фактором, ограничивающим удельные энергетические характеристики устройств, использующих газовый разряд.

Большинство теоретических моделей основывается на линейной теории устойчивости дифференциальных уравнений, определяющих порог и инкремент нарастания флуктуационных гармоник в изначально однородной среде. Причем условия положительности инкремента являются по существу верхней границей по газоразрядным параметрам, когда предельные характеристики достигаются одновременно во всей рассматриваемой области. Поэтому эти модели не подходят для исследования шнурования при наличии неоднородностей, имеющихся в реальных условиях.

Постановка задачи в общем виде, когда неоднородности заданы в виде двух- трехмерной случайной функции, при имеющихся в данное время подходах - затруднительна: линейный анализ неустойчивости дают верхнюю границу параметров, а численный эксперимент при всех его достоинствах, не позволяет выявить общих закономерностей, являющихся следствием нелинейности и наличия двух-, трехмерных случайных возмущающих полей.

Исследования процессов, происходящих в разряде при критических для шнурования условиях, показали многочисленность факторов, влияющих на порог шнурования. Необходимость учета множества взаимовлияющих факторов, приводит к сильному усложнению дифференциальных уравнений, описывающих разрядные процессы. В данное время нет аналитической модели, учитывающей взаимодействие турбулентного потока и тлеющего разряда. Вообще говоря, нет физических представлений, концепций для создания таких моделей.

Для стационарного поддержания тлеющего разряда при повышенных давлениях требуется быстрый проток газа через разрядный промежуток. Наличие газового потока не только ограничивает энерговклад в единицу массы газа и предохраняет от перегрева, но также повышает устойчивость тлеющего разряда. Однако повышение скорости потока не всегда обеспечивает однородный режим горения тлеющего разряда, а иногда повышение скорости уменьшает устойчивость. [4]. Так как диффузия и теплопроводность являются стабилизирующими факторами, то интенсификация этих процессов при турбулизации газового потока могла бы повысить устойчивость разряда. Действительно, в работе [5] было показано, что при переходе газового потока из ламинарного режима в турбулентный происходит расконтрагирование продольного разряда. Однако влияние турбулентности оказалось неоднозначным, так в работе [6] было показано, что увеличение интенсивности турбулентности иногда ухудшает устойчивость. Так как изменения линейной скорости и интенсивности турбулентности связаны между собой, то причиной изменения предельных энерговкладов может быть воздействие двух стабилизирующих факторов: конвективный вынос нагреваемого и возбуждаемого газа и перемешивание неоднородностей. Очень сложно оценить воздействие газодинамической турбулентности. В данное время общепринятой модели, адекватно описывающей генерацию и разрушение плазменных неоднородностей газодинамической турбулентностью, нет. В ряде экспериментов, используя только высокоинтенсивный турбулентный поток, удалось поддерживать стационарный самостоятельный тлеющий разряд при атмосферном давлении [7,8]. При рассмотрении процесса размешивания неоднородностей обычно используют понятие коэффициента турбулентной диффузии. Совокупное действие амбиполярной и турбулентной диффузии в работе [9] предлагают учитывать следующим образом:

D = Dа + Dturb ,

(1)

где D_a и D_turb -коэффициенты амбиполярной и турбулентной диффузии, соответственно. А в работе [10] на основании обработки экспериментальных данных [11] выведена другая формула:

,

(2)

где 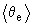- усредненная электронная температура, а 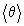- средняя газовая температура. Обе формулы считаются эмпирическими, однако, численные значения коэффициента диффузии, вычисленные по этим формулам, могут различаться. Описание турбулентного перемешивания как диффузионного процесса сводится к усреднению по пространственным масштабам много большим, чем масштаб турбулентности. Оценка эффективного коэффициента турбулентной диффузии пассивной примеси для различных модельных типов течений предпринята в работах [12]. Эффективный коэффициент диффузии может быть использован лишь для химически пассивной примеси в газе на временах много больше газодинамических. Однако электроны и ионы в газовом потоке вряд ли могут считаться пассивной примесью, так как время жизни электронно-ионной примеси, определяемое балансом ионизации и рекомбинации много меньше газодинамических времен. Другими словами, концентрация электронов и ионов определяется главным образом процессами ионизации и рекомбинации, а процессы диффузионного и конвективного переноса влияют мало на баланс носителей тока. На данном этапе нет модели, раскрывающего механизм этого воздействия турбулентного потока на тлеющий разряд. Поэтому нет количественной характеристики турбулентности, которая могла бы использоваться в оценке степени турбулентности, служить критерием качества турбулентности газового потока.

Экспериментальные исследования тлеющего разряда в турбулентных потоках проводились в широком диапазоне экспериментальных условий. Исследования проводились при скоростях газового потока, достигающих скорости звука и выше [13]. Изменения в уровне турбулентности достигалось: изменением плотности газового потока [5], изменением проходного сечения отверстий в решетках, устанавливаемых в потоке [4], изменением частоты вращения турбулизующих лопаток [15]. Изменения в уровне турбулентности неизбежны при изменениях скорости протока, однако, во многих исследованиях тлеющего разряда в газовых потоках измерений характеристик турбулентности не производилось. Влияние турбулентных пульсаций плотности газа на электронную плотность происходит в силу сильной зависимости частоты ионизации от приведенной напряженности поля E/N.

В квазистационарном случае уравнение баланса заряженных частиц имеет вид:

,

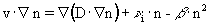(3)

где v – скорость газового потока, D – коэффициент амбиполярной диффузии,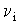- частота ионизации, 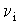=ANexp (BN/E ), А и В - const, определяемые составом газовой смеси; 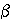- коэффициент рекомбинации, величина которой также определяется составом газовой смеси.

Для дальнейшего анализа мы должны конкретизировать каким-либо образом картину течения. Уравнения Навье-Стокса

,

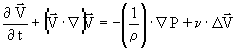(4)

формально инвариантны относительно преобразований подобия

.

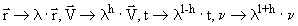(5)

Заметим, что средняя диссипация энергии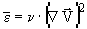 изменяется под действием преобразований подобия (5) по закону:

.

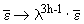(6)

Закон Колмогорова может быть получен, если потребовать инвариантность относительно преобразования подобия с h =1/3. То есть, диссипация энергии поступательного движения газа в турбулентных течениях сосредоточена на множестве с нецелой (фрактальной) размерностью.

Так как основной энергонесущий вихрь в силу гидродинамической неустойчивости порождает вихри меньшего масштаба, которые в свою очередь порождают следующий каскад вихрей, то предположим наличие в турбулентном потоке некоторого множества вихревых трубок. Эта картина является достаточно известной [16], к нему приводят, например, сценарии турбулентности связанные с удвоением цикла. Описание турбулентного течения с вихревым движением начнем с двухмерного течения в плоскости Z=const, характеризуемого полем скоростей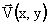. Реальная структура вихревого течения сложна, поэтому рассмотрим модельное вихревое течений.

Рассмотрим поле скоростей турбулентного потока. Условие квазистационарности для разрядных процессов считаем выполненным, так как характерные времена процессов ионизации и рекомбинации много меньше газодинамических. Предположим, что также выполнено условие квазистацинарности для газовых процессов. Тогда в уравнении непрерывности:

,

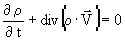(7)

первый член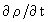= 0. Раскроем div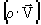, тогда имеем:

,

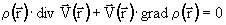(8)

где аргументом функции являются компоненты радиус-вектора 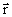или, другими словами, функци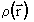ии 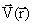являются в общем случае функциями от двух или трех переменных. Пусть имеются области, где линии, касательными к которым являются векторы скорости 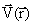, представляют собой замкнутые линии. Эти области будут представлять вихревые ячейки. Поле скоростей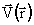в вихревых ячейках плоского течения можно свести к функции тока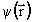, которая является обобщением функции тока на случай сжимаемого газового потока [14].

Рассмотрим сначала случай предельной турбулизации потока, когда участки с незамкнутой траекторией(x,y) вырождаются в узкие полоски, стремящиеся в пределе к линии. Тогда очевидно, что на этих линиях соответствующие функции тока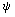(x,y)=0. Если средняя завихренность потока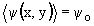, переходя к вращающейся неинерциальной системе координат, можем выбрать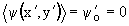. Так как функцию тока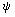(x,y) определяет поле скоростей:

,

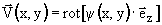(9)

то распределение нейтральных частиц N(x,y) в потоке с вихревой турбулентностью будет определяться распределением функции тока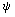(x,y), которая будет двухмерной случайной функцией: поверхность z =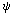(x,y) будет состоять из множества холмов и впадин, распределенных нерегулярным образом. Тогда в общем случае области знакопостоянства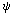(x,y) будут являться вихревыми ячейками. Размеры ячеек, их интенсивность при достаточно большом числе бифуркаций удвоений цикла будут подчиняться соответствующей спектральной функции. Линии тока, являющиеся линиями уровня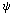(x,y) = h, можно наглядно интерпретировать как береговые линии, возникающие при последовательном затоплении водой холмистой ландшафта z =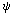(x,y) [17]. При этом имеет место резкий переход от отдельных озер на бесконечной суше к отдельным островам в бесконечном океане. В точке перехода (h=<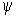>=0) существует по крайней мере одна береговая линия бесконечной протяженности. Максимальный поперечный размер d _h линий уровня 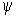(x,y) =h при h 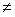0 конечен и увеличивается при h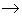0 по закону

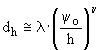
(10)

Так как линии тока 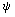=const сильно извилисты (их радиус кривизны порядка,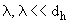), длина замкнутой линии тока L _h значительно превышает ее диаметр:

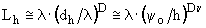
(11)

Учет диффузионно-конвективного переноса в уравнении баланса носителей тока в тлеющем разряде, осуществляемого в двухмерном турбулентном потоке, упрощается при переходе от переменных (x, y) к переменным действие угол (I- 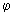), где I - площадь фигуры, окруженной линией уровня y=const, а 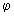- циклическая переменная на кривой уровня. Однако для этого необходимо знать функцию 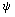(x,y), поэтому вместо переменных (I-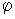) перейдем к цилиндрическим (r, 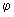), c целью проведения простейших оценок, которые затем распространим на более сложные случаи, учитывая, конечно, их неполноту. Для этого введем локальные цилиндрические системы координат, поместив ось Оz в центр i-той вихревой ячейки:

.

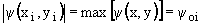(12)

Функцию тока y(x,y) в пределах вихревой ячейки предполагаем вида:

,

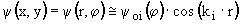(13)

где r -радиус в i-той локальной цилиндрической системе координат, 1/k _i - размер вихревой ячейки, расчеты будут проводиться только до значения 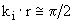.Такое описание может быть применено к турбулентным потокам не только в вихревых устройствах. Отличие газового потока в вихревых устройствах (СВТ и проч.) от потока в плоских каналах состоит том, что общая интегральная завихренность будет ненулевой:

,

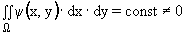(14)

где - 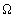область, где рассматривается газовый поток. Линии тока y(x,y) = const представляют собой траекторию частиц газа, так как вектор скорости 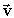(x,y) направлен по касательной к линии тока.

Рассмотрим уравнение баланса электронов (ионов) в двухкомпонентной плазме () в пределах одной k-той вихревой ячейки:

=0

(15)

где 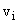(E/N) - частота ионизации, а - коэффициент рекомбинации.

Первый член, в силу замкнутости траектории, не влияет на баланс носителей тока. Однако данное движение приведет к понижению давления на оси вихревой трубки, а следовательно к увеличению параметра (Е/N). Результаты расчетов показывают, что определяющим фактором является радиальное распределение концентрации нейтральных частиц N(r), так как в диапазоне приведенных напряженностей Х = (Е/N) = (10^-15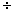10^-16), (Всм²), характерных для данного случая, частота ионизации является сильно растущей функцией от величины (Е/N). В работе [14] показано, что распределение электронов будут иметь колоколообразнную форму.

В безрасходных частях потока уравнение может быть упрощено:

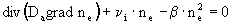
(16)

Данное уравнение разрешимо, если задано распределение плотности нейтральных частиц N(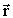). Распределение нейтральных частиц вблизи оси вихревой ячейки будет определяться уравнением:

.

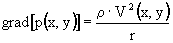(17)

Для расчета использовались следующие предположения: V(r) = 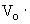sin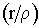, где V_о - максимальное значение скорости на периферии вихревой ячейки, было взято равными V_о=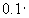U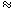3 м/с, U30 м/с; коэффициент политропы m = 1.2, относительный размер вихревой ячейки взят равным r /=. Средняя молярная масса взята для смеси СО₂: N₂: He=1 : 1 : 8, как наиболее часто встречающейся лазерной смеси для СО₂ - лазеров. Температура Т_с взята равной 300 K. Расчеты производились для различных газовых смесей, различных температур на оси, различных показателях политропы, однако все зависимости относительной плотности имеют качественно одинаковый характер с min на оси и с ростом N(r) к периферии.

Расчет уравнения N (r) c заданным распределением T(r) дает следующую зависимость:

(18)

Увеличивающееся тепловыделение приведет к росту приосевой температуры Т_o и изменит распределение , а значит и распределение N(r), а затем и всю цепочку: N(r)n(r)j(r) T(r) V(r) N(r): распределение плотности определяется распределением скоростей , распределение плотности газа N() определяет в свою очередь распределение электронной плотности n(), и, следовательно, распределение плотности электрической мощности, вкладываемой в разряд: . Распределение вложенной электрической энергии определяет распределения температуры и давления. А это в свою очередь влияет на поле скоростей. Таким образом, решение должно проводиться самосогласованным образом. Однако самосогласованное решение сложной системы сцепленных нелинейных уравнений весьма затруднительно, кроме того требуется априорное знание картины течения(x,y).

Однако вместо точного решения могут быть использованы простые оценочные решения, так как для качественного анализа необходимо выяснить основные причины необычайно высокой устойчивости тлеющего разряда в продольном вихревом тлеющем разряде, а также выяснить величину неоднородности распределения плотности тока, а значит распределения энерговкладов, что является практически значимым в случае оценки возможности использования данного типа разряда для накачки активной среды лазера.

Выше мы показали, что распределение электронной плотности в пределах вихревой ячейки имеет вид функции с максимумом на оси вихревой трубки. Если распределение электронной плотности не является односвязной, то есть, когда "виртуальная" стенка находится внутри вихревой трубки - электронная плотность спадает до нуля на замкнутой, финитной линии тока, то такой случай назовем случаем микрошнурования.

Предположим, при переходе от переменных (x,y) (r, )(I, ), где I= - площадь фигуры, ограниченной линии = const, a a = mod (t ) - циклическая переменная вдоль линии =const, качественный вид n(r) n(I) - сохраняется. Вблизи оси вихревой трубки вид функциональной связи (I - r) наиболее прост: I =, .

Обозначим площадь участка, где плотность носителей тока не нулевая, за S(j0) = I_h. Тогда задача о заполнении током вихревых ячеек аналогична перколяционной задаче о заполнении неровностей суши, поднимающейся водой (h- уровень воды) и образовании связной водной поверхности вместо системы озер. По мере роста площади I_h=S(j0), когда диффузионно-рекомбинационные процессы будут уравновешивать ионизационные на все большем удалении от оси вихревой трубки, все большую роль начнет играть конвективный уход частиц на все более длинных линиях уровня, так как длина этих линий стремиться к. Допуская постоянство n(r) на линиях тока, принадлежащих к не очень большим вихревым ячейкам будем считать, что диффузия носителей электрического заряда поперек линий функции тока const приведет к заполнению вихревой ячейки, если n(I)0.

Только вместо статистически симметричного распределения возвышенностей и впадин, мы будем иметь картину, когда все возвышенности (x,y)>0 будут отражены относительно уровня =0, так как линиям <0 и >0, отвечают вихревые ячейки, вращающиеся по часовой и против часовой стрелки. В обоих случаях на оси вихревой ячейки будет понижение плотности, а значит максимум плотности носителей электрического тока. Таким образом, вместо перехода от системы озер к системе островов имеем переход от системы озер к системе полностью заполненной водой, то есть к "всемирному потопу".

Переход от системы озер к связной поверхности будет носить пороговый характер, однако в данном случае в отличие от перколяционной задачи о катодных пятнах, порог перколяции не будет связан с порогом "катастрофического" шнурования. Рассмотрим вопрос об устойчивости к шнурованию позже. А сейчас перейдем к оценке однородности энерговклада.

Двухмерный случайный потенциал mod[] = |(x,y)| будет порождать двухмерную случайную функцию:

(19)

В данном случае предполагаем Е практически постоянными в токовом сечении. Двухмерная случайная функция n_e(x,y) приведет к двухмерной случайной функции W(x,y) = eE².

Поверхность W(x,y) будет иметь вид случайно распределенных возвышенностей. Однако, переходя от распределения W(x,y) к распределению коэффициента усиления слабого сигнала для лазеров g_o(x,y), учтем, что газовая температура T(x,y)W(x,y) тоже является случайной двухмерной функцией. Если теперь зададим зависимость g(x,y) = F[W(x,y),T(x,y)] и учтем, что g = g(T) является убывающей функцией и зануляется при определенной температуре T = T_крит., (эта температура определяется типом лазерного перехода: для СО₂ - лазеров Т_кр.= 600К, для СО- лазеров Т_кр.= 100К ), то увидим, что g = g(W) является немонотонной функцией, а имеет максимум. Это приведет к тому, что g(x,y) будет максимально в тех местах W(x,y) = W _опт. - оптимальному при заданном способе теплоотвода.

Так как теплоотвод в данном случае (внутри вихревой ячейки) является теплопроводностным, то рост размеров вихревых ячеек является весьма нежелательным. Таким образом, можно сделать вывод, что при использовании газового потока с данным типом турбулентности в качестве активной среды лазера важно добиться организации мелкомасштабной турбулентности с малыми размерами вихревых ячеек или трубок.

Выше упоминалось, что вихревой тлеющий разряд является рекордно устойчивым для стационарного самостоятельного тлеющего разряда.

Устойчивость разряда не может быть объяснена увеличением коэффициента диффузии, так как оценка эффективного коэффициента турбулентной диффузии из устойчивости приводит к заведомо завышенным значениям. Действие турбулентного потока не может быть сведено к диффузионному в силу высокой скорости электроразрядных процессов по сравнению с газодинамическими.

Рассмотрим газовый поток с вихревой турбулентностью, в котором зажигают тлеющий разряд. Вихревые нити приводят к локальным понижениям концентрации частиц газа - молекул или атомов относительно среднего уровня <N(x,y)>. По мере развития турбулентности более крупные вихревые нити порождают вихревые нити меньшего масштаба. Тогда в случае развитый турбулентности количество участков со спокойным течением уменьшается до минимума, и весь объем будет заполнен вихревыми нитями, образовавшимися в результате каскадного размножения турбулентных вихрей.

Если электрическое поле направлено вдоль вихревой нити, то сносовое размывание появляющихся неоднородностей будет минимальным, так как линии тока в данном случае образуют замкнутые линии.

Так как мгновенное локальное тепловыделение пропорционально удельному объемному энерговкладу, то распределение газовой температуры будет определяться уравнением теплового баланса. Перепад температур можно оценочно определить: , где - КПД, а t - характерное время теплоотвода. Избыточное тепловыделение из-за флуктуации плотности тока j(x,y) локализуется в приосевой области вихревой нити. Это избыточное тепловыделение q приведет к локальному перегреву T, избыточному над стационарным: T(x,y) ~, что приведет к расширению вихревой трубки, точнее, ее периферийной области, к увеличению его радиуса: .

Увеличение радиуса вихревой трубки на приведет к уменьшению тангенциальной скорости в силу закона сохранения момента импульса периферийной области вихревой трубки. Данное уменьшение тангенциальной скорости приведет к росту концентрации нейтральных частиц в приосевой области.

Если расширение газа в области локального флуктуационного превышения плотности тока в случае спокойного газового потока приводит к уменьшению концентрации N(x,y) и к дальнейшему росту плотности тока в диапазоне параметров ионизационно - перегревной неустойчивости, то наличие вихревой тубулентности приводит обратной зависимости. Поскольку эта дополнительная отрицательная обратная связь между jj определяется моментом импульса периферийной части вихревой нити или ее кинетической энергией вращательного движения: W_кин.=, то целесообразно использовать ее как энергетический параметр, характеризующий турбулентный поток с точки зрения устойчивости тлеющего разряда. Рассмотрим процесс уменьшения тангенциальной скорости вихревой нити из-за расширения более подробно.

Оценим момент импульса периферийной части вихревой трубки в отсутствии разряда:

.

(20)

Зададим N(r) - ступенчатой функцией:

(21)

где - некоторый радиус, вне которого содержится большая часть, например, - 0.9 всего момента импульса. Зададим также толщину периферийной части вихревой трубки b. Вращающаяся цилиндрическая оболочка вихревой трубки будет удерживаться центростремительной силой, образованной разностью давлений на границе раздела :

(22)

где - давление вне и внутри вихревой трубки, m - средняя масса молекул; N - концентрация молекул; V - тангенциальная скорость вращающейся оболочки; r - радиус раздела. Сократив на множители, получим:

(23)

Так как сохраняющейся величиной является момент импульса, запишем его отдельно:

.

(24)

С учетом (105) уравнение (104) запишется в следующем виде:

() .

(25)

При изменении температуры внутри вихревой трубки давление будет также меняться и будет изменяться радиус вихревой трубки. Закон сохранения числа молекул внутри вихревой трубки дает связь между N _oc, и r_L при температуре T_oc. и и при температуре :

(26)

Подставим это выражение в (25):

росев. ,

(27)

где p_средн. - давление вне вихревой трубки; L - момент импульса единицы длины вихревой трубки; N_L- значение концентрации молекул во вращающейся периферийной части вихревой трубки; - характерный радиус вихревой трубки; b - характерная толщина вращающейся оболочки; N_oc. и T_oc. - невозмущенные значения концентрации молекул и температуры внутри трубки; - концентрация молекул и температура внутри трубки, после определенного возмущения, например, положительной флуктуации тока внутри трубки. Разделим обе части уравнения (27) на среднее давление p_cредн. = kT_LN_L , и введем безразмерные и нормированные значения температуры и концентрации молекул: тогда:

.

(28)

Обозначим множитель перед относительной концентрацией в третьей степени через :

,

(29)

тогда уравнение (29) перепишется в следующем виде:

.

(30)

Определим физический смысл параметра . Для этого перепишем его через концентрацию и тангенциальную скорость:

.

(31)

Помножим знаменатель и числитель первой дроби на N_L , а знаменатель и числитель второй - на z , тогда имеем:

,

(32)

или

,

(34)

где V - объем цилиндрической оболочки; V - объем цилиндра, внутренней части вихревой трубки.

Таким образом, параметр - показывает соотношение между энергией упорядоченного движения газа и энергией теплового движения молекул единицы длины вихревой трубки. Так как на самом деле, функции N(r) и V(r) непрерывные и гладкие функции от r, то распространим уравнение (31) для связи температуры и концентрации внутри вихревой трубки на случай непрерывного распределения. Тогда, конечно, величина характерного параметра будет определена с точностью до порядка. Для оценки запишем его в ином, более удобном виде:

,

(35)

где - удельная внутренняя энергия, а - удельная энергия упорядоченного движения, Дж/кг. Для воздуха = 29 г моль, примем T = 300 К, а - примем равным 3.3 м/с и 10 м/с. Тогда .

Влияние вихревого движения, таким образом, сводится к уменьшению зависимости относительной приосевой концентрации от относительной газовой температуры на оси. Если в спокойном газе или ламинарном потоке:

,

(36)

то для газового потока внутри вихревой трубки:

,

(37)

причем 0< n <1, t >1.

После несложных преобразований получим

.

(38)

Данный параметр связывает параметры турбулентного потока: V и , параметры газовой смеси: и c, плотность энергии выделяющейся в разряде (j). Обозначим получившееся выражение как характерный энергетический параметр (ХЭП). ХЭП характеризует устойчивость тлеющего разряда в газовом потоке с вихревой турбулентностью через их параметры в совокупности.

Литература

1. Абельсиитов Г.А., Велихов Е.П., Голубев В.С., Григорянц А.Г., Лебедев Ф.В., Николаев Г.А. Мощные газоразрядные СО₂ - лазеры и их применение в технологии. М.: Наука, 1984. 106 С.
2. Мак-Таггарт Ф. Плазмохимические реакции в электрических разрядах. М.: Атомиздат, 1972. 256 С.
3. Минкевич А.Н. Химико-термическая обработка металлов и сплавов. М.: Машиностроение, 1965. 491 С.
4. Бондаренко А.В., Голубев В.С., Даньщиков Е.В., Лебедев Ф.В., Рязанов А.В. О влиянии турбулентности на устойчивость самостоятельного разряда в потоке воздуха. // Физика плазмы. 1979, Т.5, Вып.5. С. 687-692.
5. Галечян Г.А., Петросян С.И. Расконтрагирование положительного столба высокоскоростным потоком газа. // ПМТФ,1975. № 6. C.9.
6. Полулях В.П., Киселев В.И. Тлеющий разряд в турбулентном потоке. // Изв. вузов. Физика, 1977. №.5, С.125-127.
7. Волов В.Т., Ламажапов Х.Д., Марголин А.Д., Мищенко А.И., Шмелев В.М. Теория вихревого тлеющего разряда и пути создания на его основе вихревого СО₂ - лазера. // Вихревой эффект и его применение в технике: Материалы 5 Всесоюзн. научн.-техн. конф. / Куйб.авиац.ин-т. Куйбышев, 1988, С.182-184.
8. Адясов С.Ф., Воронов А.И., Катулин В.А., Михеев П.А., Николаев В.Д., Петров А.Л., Шепеленко А.А. Электроразрядный СО₂ - лазер с вихревым потоком газа. // Квантовая электроника, 1990. Т.17, № 5. С.537-542.
9. Райзер Ю.П. Основы современной физики газоразрядных процессов. М.: Наука, 1980. 416 с.
10. J.Shwartz, Y.Lavie. // AIAA J., V.13, P.647, 1975.
11. G.A.Garosi, G.Bekeffi, M.Schulz. // Phys.Fluids, V.13, P.2795, 1970.
12. Исиченко М.Б., Калда Я.Л., Татаринова Е.Б., Тельковская О.В., Яньков В.В. Диффузия в среде с вихревым движением // Журнал экспериментальной и теоретической физики, 1989. Т. 96, В 3(9). С. 913-925.
13. Галеев И.Г., Гончаров В.Е.,Тимеркаев Б.А., Торопов В.Г., Фасхутдинов А.Х. Особенности тлеющего разряда в сверхзвуковом потоке газа. // Теплофизика высоких температур. 1990. T.28, № 5. C.843-846.
14. Ламажапов Х.Д. Исследования тлеющего разряда в вихревых потоках газа. Дисс. на соиск. степени к.ф.-м.н. – М.,1998. – 114С.
15. Нефедова М.Г. Влияние турбулентности потока на максимальную мощность диффузного разряда. // Теплофизика высоких температур, 1974. Т.12, №3. С.682-685.
16. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие. В 1O т. Т.4. Гидродинамика. - М.: Наука, 1986.- 736 С.

Шкловский Б.М., Эфрос А.Л. Электрические свойства легированных полупроводников. М.: Наука, 1979. 416 С.