Media-security

РОЛЬ ДИФФУЗНОЙ ПОДСВЕТКИ ПРИ ВЫЧИТАНИИ ИЗОБРАЖЕНИЙ ФАЗОВЫХ ОБЪЕКТОВ

С. Н. Малов

Иркутский Филиал Института Лазерной Физики СО РАН

Способ получения как линзовых, так и безлинзовых голограмм Фурье [1] позволяет регистрировать и восстанавливать наиболее полный набор пространственных частот объектного поля по сравнению с другими голографическими методами. Следствием этого является получение в фурье-голографии изображений с высоким разрешением. Элементарный анализ [2] показывает, что фотодетектор (фотопластинка) протяженностью l регистрирует (а, следовательно, и восстанавливает) в схеме голографии Фурье более полный набор пространственных частот, нежели в случае голографии Френеля. В самом деле, при регистрации голограммы Френеля максимальный набор пространственных частот определяется расстоянием от объекта О до плоскости регистрации L и протяженностью фотодетектора ФД

Q ₁ = 2arctg(l/2L), (1)

где Q ₁ - интервал углов (дифракционный конус), в котором содержатся регистрируемые пространственные составляющие объектного поля. Голограмма Фурье регистрирует при тех же условиях пространственно-частотные составляющие объектного поля, распространяющиеся в дифракционном конусе Q ₂, определяемым фокусным расстоянием оптической системы

Q ₂ = 2arctg(l/2f). (2)

При условии, что L>f, при сравнении (1) и (2) получим Q ₂>Q ₁, что и требовалось доказать. Другими словами, можно говорить о повышенной плотности регистрации информации на фурье-голограмме по сравнению с другими голографическими схемами. Этим, в частности, объясняется широкое применение схем голографии Фурье при разработке и конструировании систем голографической памяти (см., например,[3]).

Последующий анализ процессов регистрации и восстановления голограмм Фурье основан на предположении, что как для формирования опорного пучка, так и восстанавливающего, используются точечные источники. Это предположение вполне оправдано тем, что эффекты, связанные с использованием протяженного источника, можно скомпенсировать [4,5]. Кроме того, рассмотрение будем проводить для одномерного случая, а также в отсутствие аберраций используемых линз.

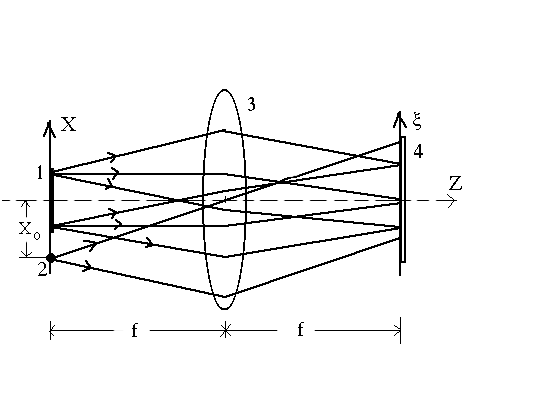
Пусть фазовый транспарант с пропусканием t(x) помещен в переднюю фокальную плоскость линзы (рис.1) и освещен нормально падающей плоской монохроматической волной единичной амплитуды. Опорная волна испускается точечным источником, расположенным также во входной плоскости [6]. Представим поле во входной плоскости x в виде

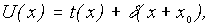(3)

где x₀ - фиксированная координата точечного опорного источника. Поле в плоскости регистрации представим в виде интеграла Фурье

Рис.1. Схема регистрации фурье-голограммы. 1 - объект, 2 - точечный опорный источник, 3 - линза, 4 - фотопластинка.

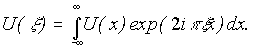(4)

Подставим (3) в (4) и перепишем последнее выражение в следующем виде

U(x )=T(x ) + exp(-2ip x_0x), (5)

где T(x ) - фурье-образ функции t(x), x = xx /l f - пространственная частота, xx - координата в фурье-плоскости, l - длина волны, f - фокусное расстояние линзы, осуществляющей фурье-преобразование. Таким образом, в плоскости регистрации интерферирует волна, представляющая собой фурье-образ объектного поля, и плоская опорная волна. Фотопластинка регистрирует распределение интенсивности

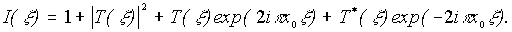(6)

Предположим, что пропускание проявленной голограммы пропорционально регистрируемому распределению интенсивностей (6), тогда освещение ее плоским пучком, нормальным к ее плоскости, приведет к формированию волны, комплексная амплитуда которой в плоскости голограммы будет описываться последним выражением. Линза, установленная за голограммой (рис. 2), будет создавать в задней фокальной плоскости поле, соответствующее обратному фурье-преобразованию восстановленной волны

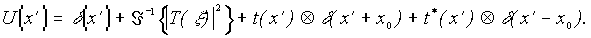(7)

Как показано на рис.2 волны, описываемые первыми двумя членами (7), будут фокусироваться в плоскости x` примерно в начале координат. Третий член представляет собой исходное пропускание, смещенное на величину х₀ относительно оптической оси. Четвертый член (7) представляет собой функцию, сопряженную и зеркально симметричную исходному пропусканию, смещенную на расстояние х₀ от оптической оси в другую сторону. Как в том, так и в другом случае дифрагированный на голограмме свет сходится, образуя действительные изображения, расположенные в одной плоскости. Поскольку фотопластинка регистрирует только распределение интенсивности, то изображения отличаются лишь тем, что одно является зеркальным отражением другого.

Рис.2. Восстановление изображения с фурье-голограммы плоской осевой волной.

Рассмотрим случай, когда в плоскость голограммы помещается фильтр (рис.3б), пропускание которого описывается выражением

t _ф=rect(x /c) (8)

где с=2r/l f, r - радиус фильтрующего отверстия. Влияние такой фильтрации на исходный пространственный спектр транспаранта (рис.3а) сводится к исключению высокочастотного диапазона (рис.3в), а это приводит в свою очередь к падению разрешения в изображении. В самом деле, рассмотрим ту часть пропускания голограммы, которая отвечает за формирование исходного распределения (третий член в (6)).

Поле в плоскости голограммы в результате фильтрации приобретает вид

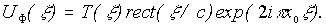(9)

Обратное фурье-преобразование последнего выражения позволяет получить распределение амплитуд, соответствующее фильтрованному изображению

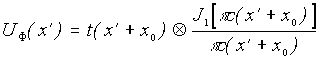. (10)

Это выражение свидетельствует о том, что каждая точка изображения из-за ограничения эффективной площади голограммы уширяется до размеров, соответствующих первому нулю функции Бесселя. Такое ухудшение разрешения является следствием того, что волновой фронт, формирующий изображение, вследствие фильтрации ограничен, т.е. реконструируется только его часть. Для повышения разрешения можно использовать метод оптического синтеза апертуры [7-9], который реализуется путем введения в обычную оптическую систему дополнительных мультиплицирующих элементов (например, дифракционных решеток).

Некоторого улучшения разрешения можно достичь, используя косое освещение объекта [10], но при этом теряется правильность передачи изображения. Другая возможность управлением разрешения по направлению, применительно к вычитанию информационных массивов, рассмотрена в [11].

Рассмотренный выше процесс регистрации фурье-голограмм (рис.1) не оптимален в случае, когда фильтрация осуществляется внеосевой малой апертурой. Такая фильтрация приводит к потере низкочастотного диапазона пространственного спектра, что сказывается на правильности передачи изображения. Пусть на этапе регистрации фурье-голограммы объект освещается плоской волной единичной амплитуды через мультиплицирующий элемент, роль которого в предельном случае может играть диффузор. Покажем, что при этом внеосевая фильтрация не приводит к существенной потере низкочастотной части пространственного спектра. Действительно, поле на выходе транспаранта в этом случае можем записать как (рис.4)

Рис.4. Схема регистрации фурье-голограмм с применением мультиплицирующего элемента 1 . 2 – транспарант, 3 - линза, 4 – фотопластинка. Опорный пучок не показан.

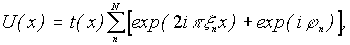(11)

где j _n - случайная фазовая добавка, которая впоследствии опускается, x _n - пространственная частота n-ой составляющей освещающего транспарант поля. Распределение амплитуд в плоскости регистрации представим в виде

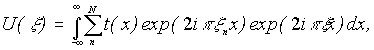(12)

где x _n = хx /l f, xx - координата в фурье-плоскости, f - фокусное расстояние линзы, l - длина волны излучения. Воспользовавшись теоремой свертки, перепишем последнее выражение

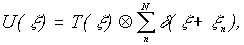(13)

которое свидетельствует о том, что в плоскости регистрации происходит мультипликация спектра, причем кратность мультипликации зависит от числа дискретных направлений, освещающих исходных транспарант волн.

Распределение интенсивностей при проведении экспозиции будет

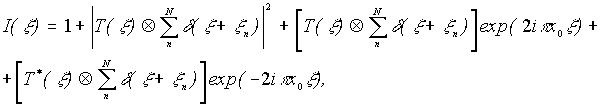(14)

где х₀ - фиксированная координата точечного опорного источника. Положим, что пропускание голограммы линейно зависит от регистрируемой интенсивности, а при восстановлении проведем пространственную фильтрацию внеосевой малой апертурой с пропусканием

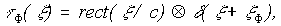(15)

где x _Ф - положение центра фильтрующего отверстия в плоскости голограммы. Отфильтрованное поле будет описываться выражением

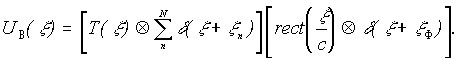(16)

Перепишем последнее выражение в более наглядном виде

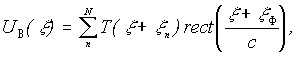(17)

из чего можно заключить, что подвергнутая фильтрации голограмма восстанавливает набор ограниченных участков исходного спектра транспаранта и, при условии применения в качестве мультиплицирующего элемента диффузора, этот набор становится избыточным, повышая тем самым помехоустойчивость голограммы.

Для распределения интенсивности в плоскости изображения можем записать

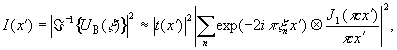(18)

где символ Á ^-1 есть оператор обратного фурье-преобразования, а J₁ - функция Бесселя. Выражение (18) свидетельствует о падении разрешения изображения за счет ограничения эффективной площади голограммы. Сумма экспонент говорит об образовании в плоскости изображения спекл-структуры. Вышесказанное позволяет утверждать, что применение мультиплицирующего элемента (диффузора) обеспечивает необходимые условия для проведения внеосевой пространственной фильтрации при идентификации отличий фазовых объектов.

Литература

Stroke G.W., Falconer D. Gr., 1964, Phys. Lett., 13, 306.

Малов С.Н., Люшаков И.В. 1997, Люминесценция и сопутствующие явления (Иркутск: Институт лазерной физики).

Толчин В.Г., Турухано В.Г., 1974, VI Школа по голографии (Л.-: ЛИЯФ).

StrokeG.W., Restrick R., Funkhouser A. and Brumm D.,1965 Phys.Lett.,18,274.

StrokeG.W., RestrickR., FunkhouserA. and BrummD.,1965, .Phys.Lett.7,178.

Lugt A.V. 1964, IEEE Trans. On Inform. Theory., IT-10, 139.

Королев А.Н., 1968, УФН, 96, 261.

Малов А.Н., Морозов В.Н., Компанец И.Н. и др. 1979, Квантовая радиофизика. Препринт №1 (Москва: ФИАН).

Морозов В.Н., Попов Ю.М., 1976, Квантовая электроника, 3, 2325.

Stroke G.W., 1966, An Introduction to Coherent Optics and Holography (New York: Academic Press).

Малов С.Н., 1990, Голографическое вычитание изображений (Иркутск: Университет).