УГЛОВАЯ ЗАВИСИМОСТЬ ДИФРАКЦИОННОЙ ЭФФЕКТИВНОСТИ ГОЛОГРАММЫ В ОБРАТИМОЙ ФОТОХРОМНОЙ СРЕДЕ
В.В. Ивахник, Е.В. Ивахник, В.И. Никонов
Самарский государственный университет
Интерес к обратимым фотохромным средам (ФХС) обусловлен прежде всего возможностью использовать их для записи динамических голограмм маломощными лазерами [1,2]. Высокое оптическое качество образцов ФХС, отсутствие ограничений по размерам, сравнительная дешевизна их получения [3] позволяет надеяться, что динамические голограммы, записанные на таких средах, окажутся конкурентно способными с динамическими голограммами, записанными на других фоточувствительных средах. Одной из основных характеристик любой голограммы, в том числе и динамической, является зависимость дифракционной эффективности голограммы (ДЭГ) от угла между волнами ее записывающими. Эта зависимость определяет, насколько точно амплитуда дифрагированной с голограммы волны соответствует амплитудам волн, записывающим голограмму. В настоящей работе анализируется угловая зависимость ДЭГ в обратимой ФХС при условии, что волны, записывающие голограмму, распространяются “навстречу” друг другу.
1. Модель фотохромной среды
Будем использовать традиционную для голографии "двухуровневую" модель ФХС. Фотохромная среда состоит из фотохромных частиц, которые могут находиться либо в состоянии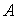 , либо в состоянии
, либо в состоянии 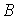 . Переход фотохромной частицы из состояния
. Переход фотохромной частицы из состояния 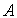 в состояние
в состояние 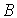 происходит под действием излучения на длине волны
происходит под действием излучения на длине волны 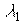 . Обратный переход фотохромной частицы осуществляется либо под действием излучения на длине волны
. Обратный переход фотохромной частицы осуществляется либо под действием излучения на длине волны 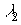 , либо спонтанно вследствие термических процессов.
, либо спонтанно вследствие термических процессов.
Кинетическое уравнение, описывающее изменение во времени концентрации фотохромных частиц в состоянии 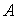 (
(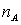 ), имеет вид:
), имеет вид:
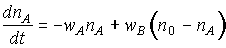 , (1)
, (1)
где 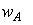 и
и 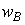 – вероятности перехода фотохромных частиц из состояния А в состояние В и обратно,
– вероятности перехода фотохромных частиц из состояния А в состояние В и обратно, 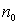 - общая концентрация фотохромных частиц. Если переход из одного состояния в другое осуществляется под воздействием излучения, то
- общая концентрация фотохромных частиц. Если переход из одного состояния в другое осуществляется под воздействием излучения, то 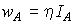 ,
, 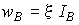 . Здесь
. Здесь 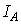 и
и 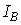 – интенсивности излучений на длинах волн
– интенсивности излучений на длинах волн 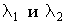 ,
, 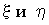 – постоянные, определяющие скорость перехода фотохромных частиц из состояния
– постоянные, определяющие скорость перехода фотохромных частиц из состояния 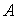 в состояние
в состояние 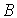 и обратно.
и обратно.
2. Запись голограммы
Пусть на слой ФХС, расположенный между плоскостями 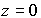 и
и 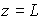 , падают две плоские волны на длине волны
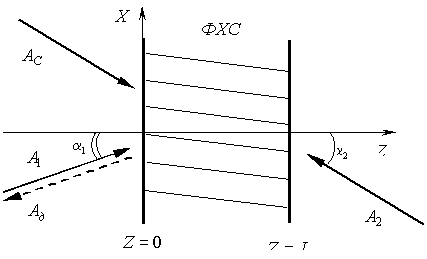
, падают две плоские волны на длине волны 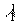 , записывающие голограмму (рис.1). Волновое уравнение, описывающее распространение в ФХС записывающих голограмму волн, есть
, записывающие голограмму (рис.1). Волновое уравнение, описывающее распространение в ФХС записывающих голограмму волн, есть
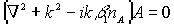 , (2)
, (2)
где 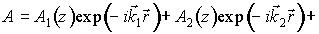 к.с.;
к.с.; 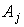 и
и 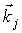 – амплитуды и волновые вектора волн, записывающих голограмму;
– амплитуды и волновые вектора волн, записывающих голограмму; 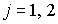 ;
; 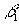 –сечение поглощения излучения на длине волны
–сечение поглощения излучения на длине волны  фотохромными частицами;
фотохромными частицами; 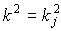 ;
; 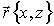 – радиус-вектор.
– радиус-вектор.
В случае записи стационарной голограммы, для установившегося режима записи, в двухволновом приближении уравнение (2) распадается на систему двух связанных дифференциальных уравнений, описывающих изменение интенсивностей записывающих голограмму волн по толщине ФХС, вида
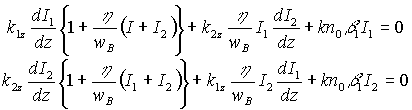 . (3)
. (3)
Здесь 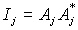 ,
, 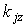 – проекция волнового вектора
– проекция волнового вектора 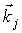 на ось Z. Если переход фотохромных частиц из состояния B в состояние A происходит под действием излучения на длине волны
на ось Z. Если переход фотохромных частиц из состояния B в состояние A происходит под действием излучения на длине волны 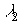 , распространяющегося строго вдоль оси Z, то система уравнений (3) дополняется уравнением, описывающим изменение вероятности
, распространяющегося строго вдоль оси Z, то система уравнений (3) дополняется уравнением, описывающим изменение вероятности 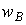 по толщине ФХС.
по толщине ФХС.
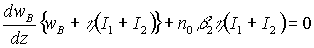 , (4)
, (4)
где 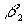 - сечение поглощения излучения на длине волны
- сечение поглощения излучения на длине волны 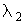 фотохромными частицами.
фотохромными частицами.
3. Считывание голограммы
Будем считывать голограмму плоской волной на длине волны 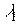 , распространяющейся навстречу волне с амплитудой
, распространяющейся навстречу волне с амплитудой 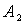 . Тогда дифрагированная волна будет распространяться навстречу волне с амплитудой
. Тогда дифрагированная волна будет распространяться навстречу волне с амплитудой 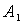 . Предположим, что распространение в голограмме считывающей и дифрагированной волн не меняет распределение коэффициента поглощения по толщине ФХС. Представим амплитуды считывающей и дифрагированной волн в виде:
. Предположим, что распространение в голограмме считывающей и дифрагированной волн не меняет распределение коэффициента поглощения по толщине ФХС. Представим амплитуды считывающей и дифрагированной волн в виде: 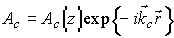 +к.с.,
+к.с., 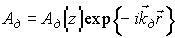 +к.с., где
+к.с., где 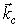 – волновой вектор считывающей волны,
– волновой вектор считывающей волны, 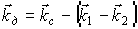 .
.
Вновь используя волновое уравнение (2), получим систему связанных дифференциальных уравнений, описывающую изменение амплитуд считывающей и дифрагированной волн по толщине голограммы, вида
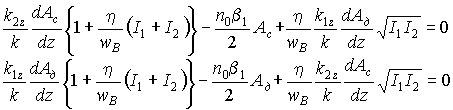 . (5)
. (5)
Эта система уравнений может быть обобщена на случай, когда направление распространения считывающей волны отличается от угла Брэгга
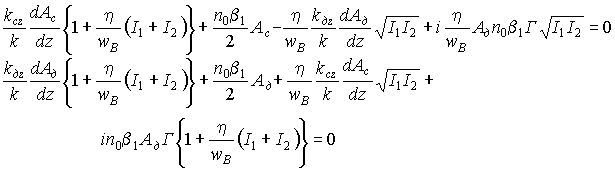 (6)
(6)
Здесь 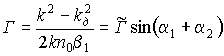 ,
,  и
и 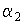 –углы между направлениями распространения записывающих голограмму волн и нормалями к граням ФХС,
–углы между направлениями распространения записывающих голограмму волн и нормалями к граням ФХС, 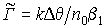 ,
, 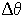 - угол, задающий отклонение считывающей волны от угла Брэгга,
- угол, задающий отклонение считывающей волны от угла Брэгга, 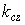 и
и 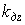 - проекции векторов
- проекции векторов  и
и  на ось Z.
на ось Z.  Полученные системы уравнений необходимо дополнить граничными условиями: для записывающих голограмму волн
Полученные системы уравнений необходимо дополнить граничными условиями: для записывающих голограмму волн
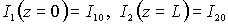 ,
,
для считывающей и дифрагированной с голограммы волн
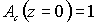 ,
, 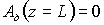 .
.
Выражения (3)-(6) с учетом граничных условий позволяют численными методами проанализировать зависимость дифракционной эффективности голограммы (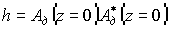 )) от характеристик ФХС, параметров волн, записывающих и считывающих голограмму.
)) от характеристик ФХС, параметров волн, записывающих и считывающих голограмму.
4. Обсуждение результатов
Кривая зависимости ДЭГ от толщины голограммы при считывании волной, распространяющейся строго под углом Брэгга, существенным образом зависит от соотношения параметров 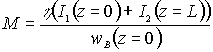 и
и 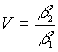 . При условии, что
. При условии, что 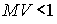 и интенсивность одной из волн, записывающих голограмму, намного больше интенсивности другой волны, с увеличением толщины голограммы ДЭГ вначале возрастает, достигает максимального значения, а затем плавно уменьшается до нуля. При
и интенсивность одной из волн, записывающих голограмму, намного больше интенсивности другой волны, с увеличением толщины голограммы ДЭГ вначале возрастает, достигает максимального значения, а затем плавно уменьшается до нуля. При 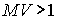 с ростом толщины голограммы ДЭГ выходит на постоянный уровень, величина которого определяется параметром
с ростом толщины голограммы ДЭГ выходит на постоянный уровень, величина которого определяется параметром 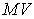 .
.
На рис.2 приведены характерные графики зависимости оптимальной толщины голограммы (т.е. толщины, при которой ДЭГ достигает наибольшего значения (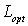 )) и соответствующей ей дифракционной эффективности (
)) и соответствующей ей дифракционной эффективности (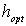 ) от параметра
) от параметра 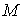 . В отсутствие зависимости вероятности перехода фотохромных частиц из состояния В в состояние А от толщины ФХС (
. В отсутствие зависимости вероятности перехода фотохромных частиц из состояния В в состояние А от толщины ФХС (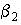 =0) изменение оптимальной толщины голограммы от параметра
=0) изменение оптимальной толщины голограммы от параметра 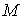 носит линейный характер. Учет изменения интенсивности стирающего излучения по толщине ФХС приводит к увеличению скорости изменения оптимальной толщины с ростом параметра
носит линейный характер. Учет изменения интенсивности стирающего излучения по толщине ФХС приводит к увеличению скорости изменения оптимальной толщины с ростом параметра 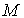 . ДЭГ, соответствующая оптимальной толщине голограммы, с ростом параметра М увеличивается, стремясь при
. ДЭГ, соответствующая оптимальной толщине голограммы, с ростом параметра М увеличивается, стремясь при 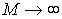 к некоторой постоянной величине.
к некоторой постоянной величине.
Уменьшение угла между волнами, записывающими голограмму, приводит к уменьшению 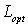 . При этом значение ДЭГ, соответствующее оптимальной толщине голограммы, не изменяется. Уменьшение контраста записываемой интерференционной решетки путем изменения относительной интенсивности волн
. При этом значение ДЭГ, соответствующее оптимальной толщине голограммы, не изменяется. Уменьшение контраста записываемой интерференционной решетки путем изменения относительной интенсивности волн 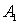 и
и 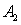 приводит к увеличению оптимальной толщины голограммы. При
приводит к увеличению оптимальной толщины голограммы. При  зависимость
зависимость  от параметра
от параметра 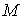 линейная.
линейная.
Характер зависимости
 и
и 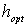 от параметра М при записи голограммы волнами, распространяющимися
“навстречу друг другу”, совпадает с зависимостью этих величин
от параметра
от параметра М при записи голограммы волнами, распространяющимися
“навстречу друг другу”, совпадает с зависимостью этих величин
от параметра 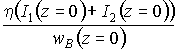 при записи голограммы “попутными” волнами [4].
при записи голограммы “попутными” волнами [4].
 |
|
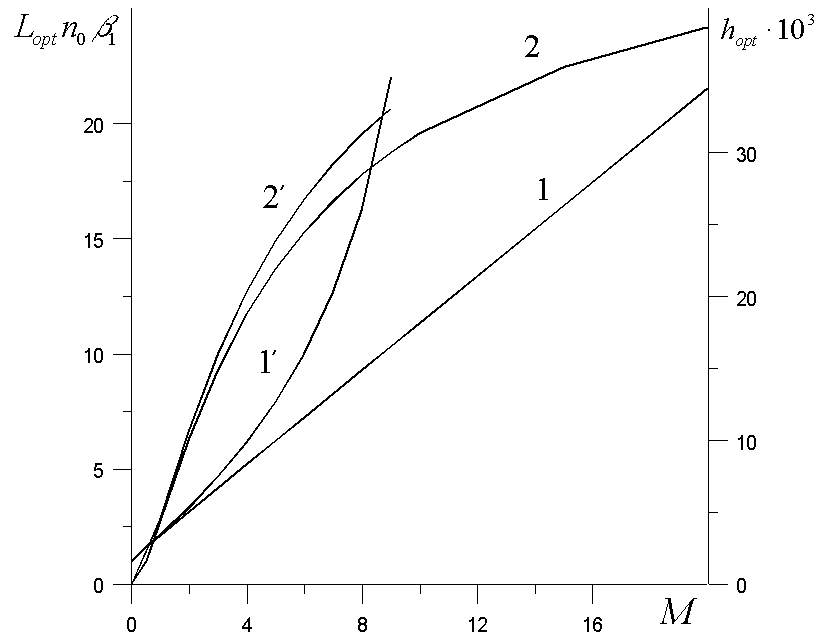 |
|
Будем записывать голограмму встречными волнами, одна из которых, например волна 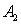 , распространяется строго вдоль оси
, распространяется строго вдоль оси 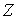 (
(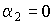 ). Анализ зависимости относительной ДЭГ (
). Анализ зависимости относительной ДЭГ (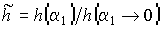 ) от угла между направлением распространения волны
) от угла между направлением распространения волны 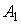 и нормалью к поверхности ФХС показывает, что при
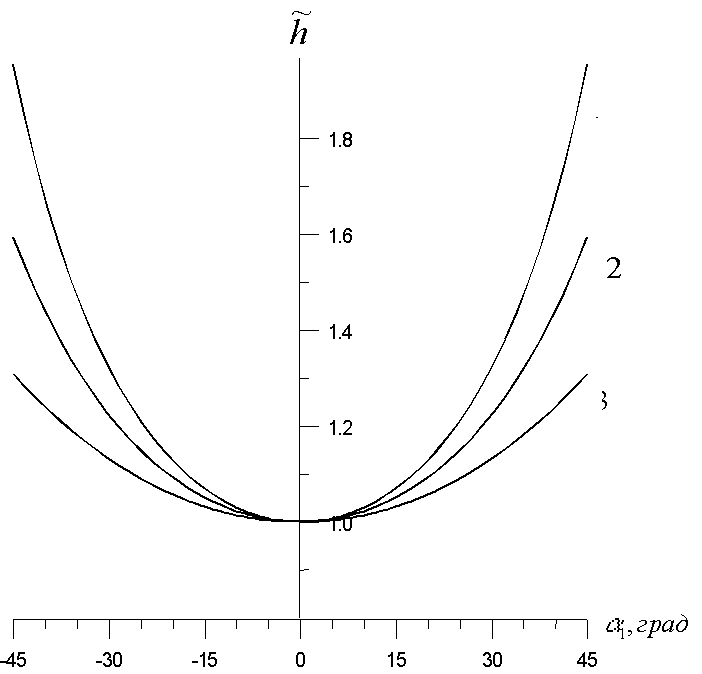
и нормалью к поверхности ФХС показывает, что при 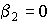 с ростом угла наблюдается увеличение относительной ДЭГ (рис.3). Наибольшая скорость изменения относительной ДЭГ характерна для тонких голограмм (
с ростом угла наблюдается увеличение относительной ДЭГ (рис.3). Наибольшая скорость изменения относительной ДЭГ характерна для тонких голограмм (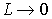 ). С увеличением толщины голограммы скорость изменения угловой зависимости относительной ДЭГ уменьшается, и при
). С увеличением толщины голограммы скорость изменения угловой зависимости относительной ДЭГ уменьшается, и при 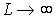 зависимость ДЭГ от угла
зависимость ДЭГ от угла 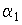 исчезает. При наличии стирающего излучения на длине волны
исчезает. При наличии стирающего излучения на длине волны 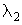 , распространяющегося строго вдоль оси Z, вид зависимости
, распространяющегося строго вдоль оси Z, вид зависимости 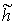 от
от 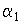 не меняется. В случае МV>1 можно выделить толщину голограммы, начиная с которой дальнейшее увеличение толщины голограммы не приводит к изменению угловой зависимость относительной ДЭГ.
не меняется. В случае МV>1 можно выделить толщину голограммы, начиная с которой дальнейшее увеличение толщины голограммы не приводит к изменению угловой зависимость относительной ДЭГ.
На рис.4 приведены графики зависимости ДЭГ от параметра 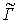 , характеризующего отклонение считывающей волны от угла Брэгга. С увеличение отклонения направления распространения считывающей волны от угла Брэгга происходит уменьшение ДЭГ. При фиксированной толщине голограммы и
, характеризующего отклонение считывающей волны от угла Брэгга. С увеличение отклонения направления распространения считывающей волны от угла Брэгга происходит уменьшение ДЭГ. При фиксированной толщине голограммы и 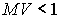 , характер зависимости ДЭГ от параметра
, характер зависимости ДЭГ от параметра 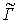 описывается функцией вида
описывается функцией вида 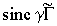 (g
- коэффициент пропорциональности). Ширина первого максимума этой зависимости определяется углом между волнами, записывающими голограмму. При
(g
- коэффициент пропорциональности). Ширина первого максимума этой зависимости определяется углом между волнами, записывающими голограмму. При 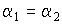 уменьшение угла между волнами, записывающими голограмму, приводит к сужению области параметра
уменьшение угла между волнами, записывающими голограмму, приводит к сужению области параметра 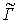 , в пределах которой происходит эффективная перекачка энергии из считывающей волны в дифрагированную волну. Увеличивается максимальное значение ДЭГ, соответствующее распространению считывающей волны строго под углом Брэгга. Если соотношение
, в пределах которой происходит эффективная перекачка энергии из считывающей волны в дифрагированную волну. Увеличивается максимальное значение ДЭГ, соответствующее распространению считывающей волны строго под углом Брэгга. Если соотношение 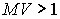 , то увеличение отклонения считывающей волны от угла Брэгга приводит к монотонному уменьшению ДЭГ до нуля.
, то увеличение отклонения считывающей волны от угла Брэгга приводит к монотонному уменьшению ДЭГ до нуля.
Отклонение считывающей волны от угла Брэгга приводит к изменению угловой зависимости ДЭГ. При 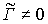 с ростом угла
с ростом угла  дифракционная эффективность голограммы уменьшается. Для характеристики селективных свойств голограммы введем понятие ширины полосы углов
дифракционная эффективность голограммы уменьшается. Для характеристики селективных свойств голограммы введем понятие ширины полосы углов 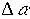 , определяемую из условия
, определяемую из условия
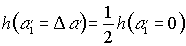 . (7)
. (7)
Численный анализ уравнений (3), (6) с учетом граничных условий показывает, что ширина полосы углов обратно пропорциональна углу, характеризующему отклонение считывающей волны от угла Брэгга, и (при небольшой толщине) толщине голограммы
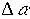 ~
~ 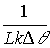 .
.
Существует критическое значение толщины голограммы, начиная с которой дальнейшее увеличение толщины голограммы не приводит к изменению ширины полосы углов.
В заключение отметим, что значения дифракционной эффективности голограмм, записанных в схемах с “попутными” и “встречными” волнами примерно совпадают.
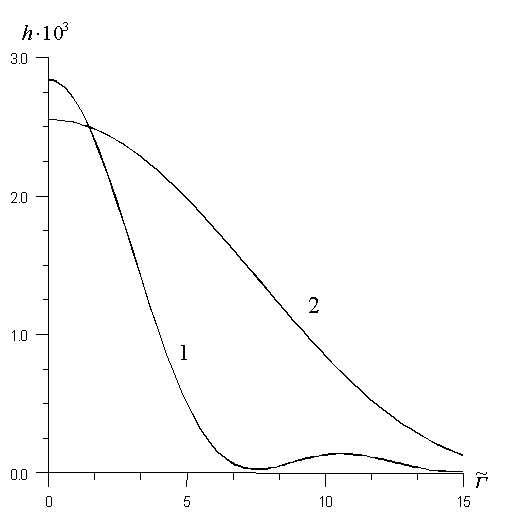
Литература
- Гуськова В.Н., Жукова В.А., Ивахник В.В. Опт. и спектроскопия. 1991. Т.70. В.2. С.431-435.
- Алятина Н.Н., Жукова В.А., Ивахник В.В., Туниманова И.В., Цехомский В.А. Оптико-механическая промышленность. 1989. ?
12. С.32-34.
- Барачевский В.А., Лашков Г.А. Цехомский С.Н. Фотохромизм и его применение. М.: Химия. 1977. 279с.
Ивахник В.В., Ивахник Е.В., Никонов В.И. Опт. и спектроскопия. 1999. Т.86. №5. С.851-855.

