ДИФРАКЦИОННАЯ ЭФФЕКТИВНОСТЬ ГОЛОГРАММЫ ОБЪЕКТА, СОВЕРШАЮЩЕГО УГЛОВЫЕ КОЛЕБАНИЯ
В.В. Ивахник, Н.П. Козлов
Самарский государственный университет
При записи на реверсивной среде голограммы нестационарного процесса при определенных условиях возникает временная зависимость дифракционной эффективности голограммы, по характеру которой можно судить о параметрах исследуемого процесса [1,2]. До сих пор основное внимание уделялось изучению дифракционной эффективности голограмм объектов, которые, модулируя фазу прошедшей (или отраженной) волн, заставляют по определенному закону двигаться по реверсивной среде записываемую голографическую решетку, не меняя при этом период решетки.
Другой не менее интересный с практической точки зрения случай - запись на реверсивной среде решетки, период которой меняется во времени. Именно этот случай реализуется при записи на реверсивной среде голограммы объекта, совершающего угловые колебания.
В качестве реверсивной среды рассмотрим обратимую фотохромную среду. Пусть среда состоит из фотохромных частиц общей концентрации 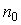 , которые могут находиться в двух состояниях А и В. Кинетическое уравнение, описывающее изменение концентрации фотохромных частиц в состоянии А есть
, которые могут находиться в двух состояниях А и В. Кинетическое уравнение, описывающее изменение концентрации фотохромных частиц в состоянии А есть
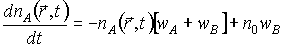 , (1)
, (1)
где 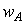 и
и 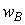 - вероятности перехода фотохромных частиц из состояния А в состояние В и наоборот,
- вероятности перехода фотохромных частиц из состояния А в состояние В и наоборот, 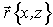 - радиус вектор. Если переход фотохромных частиц из состояния А в состояние В происходит под действием излучения на длине волны l
, то
- радиус вектор. Если переход фотохромных частиц из состояния А в состояние В происходит под действием излучения на длине волны l
, то 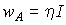 (I - интенсивность излучения, h
- коэффициент пропорциональности).
(I - интенсивность излучения, h
- коэффициент пропорциональности).
Двумя плоскими волнами на длине волны l
будем записывать тонкую голограмму (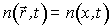 ). Одна волна распространяется вдоль оси Z, вторая, отражаясь от плоского зеркала, падает на фотохромную среду под углом
). Одна волна распространяется вдоль оси Z, вторая, отражаясь от плоского зеркала, падает на фотохромную среду под углом 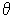 к оси Z (рис.1). Распределение интенсивности в плоскости фотохромной среды можно представить в виде
к оси Z (рис.1). Распределение интенсивности в плоскости фотохромной среды можно представить в виде
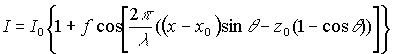 . (2)
. (2)
Здесь 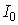 - средняя интенсивность,
- средняя интенсивность, 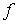 - глубина модуляции записываемой интерференционной решетки,
- глубина модуляции записываемой интерференционной решетки, 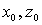 - координаты точки углового поворота зеркала.
- координаты точки углового поворота зеркала.
Разложим концентрацию фотохромных частиц в пространственный спектр
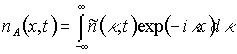 . (3)
. (3)
Здесь 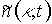 - амплитуда гармонической решетки концентрации фотохромных частиц с пространственной частотой
- амплитуда гармонической решетки концентрации фотохромных частиц с пространственной частотой 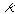 .
.
Рис.1. Схема записи голограммы
Если запись голограммы осуществляется на неограниченной по поперечным размерам фотохромной среде, то после подстановки (3) в (1) с учетом (2) получим уравнение, описывающее изменение во времени амплитуды пространственного спектра фотохромных частиц,
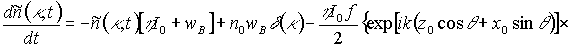
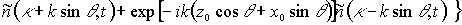 , (4)
, (4)
где 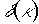 - дельта функция.
- дельта функция.
При выполнении начального условия
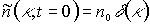 (5)
(5)
амплитуда спектра на нулевой пространственной частоте есть
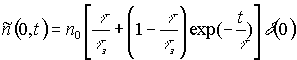 , (6)
, (6)
где 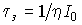 - время записи голограммы,
- время записи голограммы, 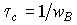 - время стирания голограммы,
- время стирания голограммы, 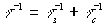 .
.
Для установившегося режима записи голограммы 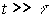 из (4) с учетом (6) амплитуду решетки концентрации фотохромных частиц с пространственной частотой k
можно записать в виде
из (4) с учетом (6) амплитуду решетки концентрации фотохромных частиц с пространственной частотой k
можно записать в виде
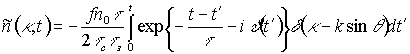 . (7)
. (7)
Здесь 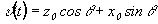 . При записи стационарной решетки (
. При записи стационарной решетки (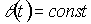 ) из (7) имеем
) из (7) имеем
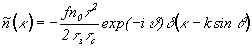 . (8)
. (8)
Будем считывать голограмму плоской волной на длине волны l
. Тогда пространственный спектр амплитуды поля за голограммой (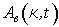 ) определяется амплитудой пространственного спектра решетки концентрации фотохромных частиц.
) определяется амплитудой пространственного спектра решетки концентрации фотохромных частиц.
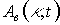 ~
~
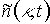 .
.
Пусть поворот зеркала меняет по гармоническому закону угол между записывающими голограмму волнами: 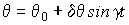 (
(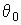 - средний угол,
- средний угол, 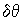 и g
- амплитуда и частота угловых колебаний). Решетка концентрации фотохромных частиц является негармонической, поэтому при неограниченных размерах фоточувствительной среды с голограммы восстанавливается набор плоских волн с пространственными частотами от
и g
- амплитуда и частота угловых колебаний). Решетка концентрации фотохромных частиц является негармонической, поэтому при неограниченных размерах фоточувствительной среды с голограммы восстанавливается набор плоских волн с пространственными частотами от 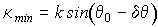 до
до 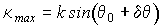 . На характер временной зависимости амплитуды волны, восстановленной с голограммы, влияет направление распространения этой волны. Амплитуда восстановленной волны меняется периодически с периодом равным периоду колебаний зеркала. На периоде наблюдается один (наблюдение ведется в направлении крайних пространственных частот) или два максимума. Положение максимумов на кривой временной зависимости амплитуды волны, восстановленной в направлении, определяемом пространственной частотой
. На характер временной зависимости амплитуды волны, восстановленной с голограммы, влияет направление распространения этой волны. Амплитуда восстановленной волны меняется периодически с периодом равным периоду колебаний зеркала. На периоде наблюдается один (наблюдение ведется в направлении крайних пространственных частот) или два максимума. Положение максимумов на кривой временной зависимости амплитуды волны, восстановленной в направлении, определяемом пространственной частотой 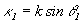 , описывается формулами
, описывается формулами
 ,
, 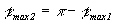 , (9)
, (9)
полученными из условия 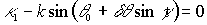 . При выполнении этого условия подинтегральное выражение в (7) стремится к бесконечности. Функция
. При выполнении этого условия подинтегральное выражение в (7) стремится к бесконечности. Функция 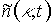 принимает максимальное значение.
принимает максимальное значение.
Зная направление наблюдения, средний угол и положение максимумов на кривой зависимости амплитуды восстановленной волны от времени, можно найти амплитуду колебаний зеркала
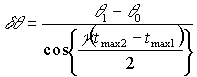 . (10)
. (10)
Учет конечности поперечных размеров фотохромной среды, на которой записывается голограмма, существенно усложняет уравнение, описывающее изменение во времени амплитуды пространственного спектра решетки фотохромных частиц. Поэтому в этом случае удобнее численными методами решить уравнение (1) с учетом (2), а затем, используя преобразование Фурье, найти амплитуду пространственного спектра.
На рис.2 приведены характерные временные зависимости относительной амплитуды восстановленной волны (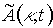 =
=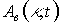 /a, а –поперечный размер фотохромной среды) при условии, что запись голограммы происходит на фотохромной среде конечных размеров, для установившегося режима записи голограммы. Как и в случае голограммы, записанной на неограниченной по поперечным размерам фотохромной среде, положение максимумов на временной зависимости амплитуды восстановленной волны хорошо описывается формулами (9).
/a, а –поперечный размер фотохромной среды) при условии, что запись голограммы происходит на фотохромной среде конечных размеров, для установившегося режима записи голограммы. Как и в случае голограммы, записанной на неограниченной по поперечным размерам фотохромной среде, положение максимумов на временной зависимости амплитуды восстановленной волны хорошо описывается формулами (9).
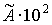
Численный анализ уравнения (1) с учетом (2) показывает, что амплитуда восстановленной волны максимальна в направлениях наблюдения 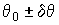 . Эти углы соответствуют крайним положениям колеблющегося зеркала.
. Эти углы соответствуют крайним положениям колеблющегося зеркала.
Если наблюдение восстановленной волны производится в направлении, задаваемым углом 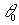 , то при фиксированных временах
, то при фиксированных временах 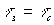 увеличении амплитуды колебаний зеркала приводит к уменьшению максимумов на временной зависимости амплитуды восстановленной волны. Глубина модуляции временной зависимости амплитуды восстановленной волны с ростом
увеличении амплитуды колебаний зеркала приводит к уменьшению максимумов на временной зависимости амплитуды восстановленной волны. Глубина модуляции временной зависимости амплитуды восстановленной волны с ростом 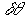 увеличивается, выходя на некоторое “среднее” значение, относительно которого при дальнейшем увеличении амплитуды колебаний зеркала и происходит осциллирующее изменение этой величины. Это “среднее” значение возрастает, а амплитуда осцилляций уменьшается с уменьшением параметра
увеличивается, выходя на некоторое “среднее” значение, относительно которого при дальнейшем увеличении амплитуды колебаний зеркала и происходит осциллирующее изменение этой величины. Это “среднее” значение возрастает, а амплитуда осцилляций уменьшается с уменьшением параметра 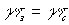 . В случае
. В случае 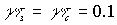 ,
,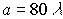 ,
, 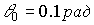 значение глубины модуляции V=0.1 наблюдается при амплитуде колебаний
значение глубины модуляции V=0.1 наблюдается при амплитуде колебаний 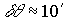 , при этом выход глубины модуляции на “среднее” значение происходит при
, при этом выход глубины модуляции на “среднее” значение происходит при 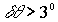 .
.
Значения максимумов на временной зависимости амплитуды восстановленной волны существенным образом зависят от времени записи и времени стирания голограммы. При 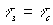 увеличение параметра
увеличение параметра 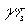 приводит к размытию максимумов и к монотонному уменьшению их значений. Если
приводит к размытию максимумов и к монотонному уменьшению их значений. Если 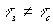 , то для фиксированного значения времени записи голограммы существует значение времени стирания голограммы, меньше чем время записи голограммы, при котором амплитуда восстановленной в некотором направлении волны максимальна. Разность времени записи и времени стирания. при которой амплитуда восстановленной волны максимальна, увеличивается с увеличением времени записи голограммы.
, то для фиксированного значения времени записи голограммы существует значение времени стирания голограммы, меньше чем время записи голограммы, при котором амплитуда восстановленной в некотором направлении волны максимальна. Разность времени записи и времени стирания. при которой амплитуда восстановленной волны максимальна, увеличивается с увеличением времени записи голограммы.
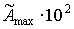
На рис.3 приведена зависимость максимального значения относительной амплитуды восстановленной волны от поперечных размеров фотохромной среды при расположении точки углового поворота зеркала на краю фотохромной среды (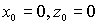 ). С увеличением размеров фотохромной среды наблюдается осциллирующее с периодом
). С увеличением размеров фотохромной среды наблюдается осциллирующее с периодом 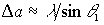 уменьшение величины максимумов амплитуды восстановленной волны. Характер приведенной зависимости можно объяснить следующим образом.
уменьшение величины максимумов амплитуды восстановленной волны. Характер приведенной зависимости можно объяснить следующим образом.
По мере удаления от точки углового поворота зеркала скорость перемещения интерференционных полос возрастает, уменьшается глубина модуляции записываемой решетки концентрации фотохромных частиц. Поэтому основной вклад в амплитуду восстановленной волны дает область фотохромной среды, расположенная вблизи точки углового поворота зеркала. Увеличение поперечных размеров фотохромной среды приводит к выходу величины амплитуды восстановленной волны на постоянной значение и, соответственно, к уменьшению относительной амплитуды восстановленной волны.
Амплитуда волны, восстановленной в направлении 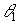 , является результатом интерференции волн, восстановленных на всех решетках, записанных в фотохромной среде. При этом в направлении
, является результатом интерференции волн, восстановленных на всех решетках, записанных в фотохромной среде. При этом в направлении 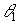 основной вклад в результат интерференции будут давать волны, соответствующие решетке с пространственной частотой
основной вклад в результат интерференции будут давать волны, соответствующие решетке с пространственной частотой 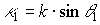 и решетке с нулевой пространственной частотой. Изменение размеров голограммы приводит к осциллирующей зависимости амплитуды волны, даваемой в направлении
и решетке с нулевой пространственной частотой. Изменение размеров голограммы приводит к осциллирующей зависимости амплитуды волны, даваемой в направлении 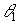 решеткой с нулевой пространственной частотой, что и объясняет наличие максимумов и минимумов на графике, приведенном на рис.3.
решеткой с нулевой пространственной частотой, что и объясняет наличие максимумов и минимумов на графике, приведенном на рис.3.
Численный анализ показывает, что максимальное значение амплитуды восстановленной волны слабо меняется при смещении точки углового поворота зеркала, расположенной на поверхности фоточувствительной среды, относительно этой среды. Выход точки углового поворота за поперечные размеры фоточувствительной среды приводит к быстрому уменьшению амплитуды восстановленной волны. Так при 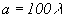 ,
, 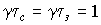 ,
, 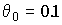 ,
, 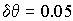 ,
, 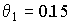 ,
, 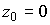 смещение точки углового поворота зеркала относительно края фоточувствительной среды на расстояние равное размеру фоточувствительной среды приводит к уменьшению максимального значения амплитуды восстановленной волны почти в два раза.
смещение точки углового поворота зеркала относительно края фоточувствительной среды на расстояние равное размеру фоточувствительной среды приводит к уменьшению максимального значения амплитуды восстановленной волны почти в два раза.
Амплитуда восстановленной волны уменьшается также с увеличением расстояния от точки углового поворота зеркала до поверхности фоточувствительной среды. Однако это уменьшение происходит значительно медленнее, чем уменьшение амплитуды восстановленной волны при смещении точки углового поворота зеркала вдоль поверхности фоточувствительной среды.
Сдвиг точки углового поворота зеркала за поверхность фоточувствительной среды приводит к возникновению дополнительной разности фаз между волнами, записывающими голограмму, которую при 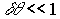 можно представить в виде
можно представить в виде
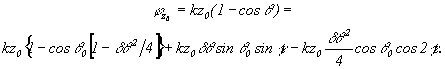 (11)
(11)
Второе и третье слагаемые в (11) свидетельствуют о том, что при 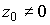 наряду с изменением периода записываемой решетки происходит периодическое смещение этой решетки (с частотой g
- второе слагаемое, с частотой 2g
- третье слагаемое) как целого по фотохромной среде. Как показано в [1] периодическое перемещение интерференционной решетки по реверсивной фоточувствительной среде начинает оказывать влияние на амплитуду восстановленной волны при условии, что амплитуда модуляции фазы не меньше p
. Тогда минимальное значение
наряду с изменением периода записываемой решетки происходит периодическое смещение этой решетки (с частотой g
- второе слагаемое, с частотой 2g
- третье слагаемое) как целого по фотохромной среде. Как показано в [1] периодическое перемещение интерференционной решетки по реверсивной фоточувствительной среде начинает оказывать влияние на амплитуду восстановленной волны при условии, что амплитуда модуляции фазы не меньше p
. Тогда минимальное значение 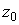 , начиная с которого возникает зависимость
, начиная с которого возникает зависимость 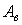 от смещения точки углового поворота колеблющегося зеркала, определяется как наименьшее значение величин
от смещения точки углового поворота колеблющегося зеркала, определяется как наименьшее значение величин 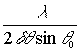 и
и 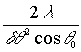 .
.
В заключении отметим, что характер зависимости амплитуды восстановленной волны от параметров волн, записывающих голограмму, характеристик фотохромной среды не меняется, если наблюдение восстановленной волны происходит не в строго определенном направлении, а в некотором угловом интервале при условии, что величина этого интервала намного меньше значений 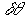 ,
, 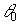 .
.
Литература
- Гаращук В.П., Гаращук Т.П., Ивахник В.В., Камшилин. // Письма в ЖТФ. 1988. Т.14. В.17. С.1583-1587.
Алятина Н.Н., Жукова В.А., Ивахник В.В., Туниманова И.В., Цехомский В.А. // Оптико-механическая промышленность. 1989. ?
12. С.32-34.

