ВЗАИМОДЕЙСТВИЕ ДЛИННЫХ НЕЛИНЕЙНЫХ ВОЛН КЕЛЬВИНА
С.В. Ловцов, Ю.В. Парфенов, А.Э. Растегин
Научно-исследовательский институт прикладной физики ИГУ
Кафедра теоретической физики ИГУ
В течение ряда лет в южной части озера Байкал в зимний период проводились гидрофизические наблюдения, по результатам первичного анализа которых был сделан вывод о распространении в южном Байкале внутренних волн Кельвина с длительностями до нескольких суток [1, 2]. Рассмотрение этого предположения в рамках линейной теории показало, что, несмотря на удовлетворительное согласие в первом приближении, линейный подход не позволяет дать содержательное объяснение некоторым характерным особенностям наблюдающихся процессов. В связи с этим была поставлена задача исследования динамики длинных слабонелинейных волн Кельвина.
Начиная с 70-х годов, нелинейные модели, в том числе уравнение Кортевега - де Фриза (КдФ) и модифицированное уравнение КдФ (мКдФ), широко используются в геофизической гидродинамике для описания внутренних гравитационных волн [3], планетарных волн [4] и береговых захваченных волн [5]. Однако большинство полученных здесь результатов относится к случаю индивидуальной динамики одной возбужденной моды (что является некоторой идеализацией). В то же время последние исследования показывают, что ряд известных явлений находят содержательное толкование в рамках представлений о совокупности взаимодействующих элементарных структур. Данные наблюдений, проводимых на протяжении ряда лет в южном Байкале, указывают на распространение уединенных волн в нескольких связанных модах. При этом имеет место обмен энергией между распространяющимися квазиустойчивыми образованиями.
В настоящей работе изложен вывод модельной системы уравнений, описывающей распространение и взаимодействие длинных слабонелинейных волн Кельвина. Эта система является обобщением известной модели КдФ на случай возбуждения нескольких вертикальных мод. Развитие данной схемы представляет определенный интерес, так как во многих работах нелинейные модели используются без обоснования их применимости к моделируемым процессам. Например, в работе [6] (где анализируются результаты наблюдения в озере Бабине длинных нелинейных внутренних волн с длительностями порядка нескольких суток, а также обсуждаются с привлечением модели КдФ общие аспекты проблемы длинных нелинейных волн в озерах) не учитывается затухание амплитуды волн при удалении от берега. В предлагаемом здесь подходе это затухание учитывается, поскольку оно существенно для наблюдающихся в южном Байкале волн (радиус деформации Россби оказывается порядка трех километров, что значительно меньше поперечных размеров южного Байкала).
Систему уравнений движения составляют (см., напр., [7]) уравнение баланса импульса
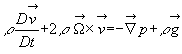 , (1)
, (1)
уравнение непрерывности
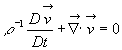 , (2)
, (2)
уравнение адиабатичности
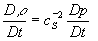 , (3)
, (3)
где 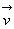 - вектор скорости жидкости, p – давление, r
- плотность жидкости,
- вектор скорости жидкости, p – давление, r
- плотность жидкости, 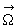 - вектор угловой скорости вращения Земли,
- вектор угловой скорости вращения Земли, 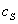 - скорость звука, а субстанциональная производная
- скорость звука, а субстанциональная производная
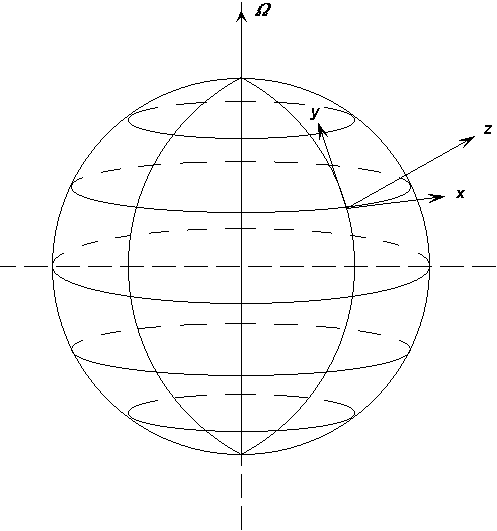
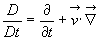 .
.
В локальной декартовой системе координат (x, y, z), где вектор скорости 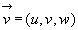 , векторное уравнение (1) даст три уравнения
, векторное уравнение (1) даст три уравнения
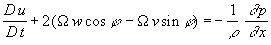 ,
,
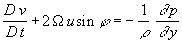 , (4)
, (4)
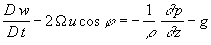 ,
,
где j
- широта точки, принимаемой за начало координат. Способ введения локальной декартовой системы координат показан на рис.1.
Если береговая линия является прямой, непараллельной осям x и y, то удобно повернуть систему координат в плоскости (x, y) на некоторый угол g
так, чтобы в новых координатах уравнение береговой линии имело вид x’ = 0. Система (4) примет вид

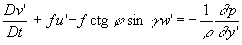 , (5)
, (5)
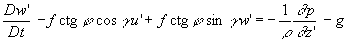 ,
,
где 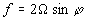 - параметр Кориолиса (рассматриваемая далее модель ограничивается средними широтами). Если бы береговой склон являлся вертикальной стенкой, то граничное условие на берегу имело бы вид
- параметр Кориолиса (рассматриваемая далее модель ограничивается средними широтами). Если бы береговой склон являлся вертикальной стенкой, то граничное условие на берегу имело бы вид
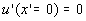 . (6)
. (6)
В действительности, однако, это не так, и при распространении волн Кельвина вдоль реального берегового склона они диспергируют. Тем не менее, если не стремиться детально исследовать движение жидкости в шельфовой зоне, то распространение длинных волн Кельвина можно описывать, используя граничное условие в форме (6), но введя в уравнение баланса импульса модель дисперсии. При этом второе уравнение системы (5) заменяется на
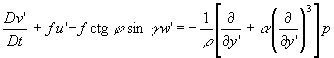 . (7)
. (7)
Здесь a
- параметр, характеризующий влияние дисперсии на длинные волны Кельвина; это влияние предполагается малым. Граничное условие (6) удобно тем, что позволяет разделить горизонтальную и вертикальную зависимости. Кроме (6), на скорость налагается условие непротекания на дне и на поверхности жидкости (последнее известно как приближение “твердой крышки”)
w(z’=-H )=0, w(z’=0)=0. (8)
Среда считается полубесконечной по оси x, поэтому используется стандартное условие захвата энергии волн берегом:
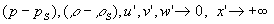 . (9)
. (9)
Здесь 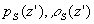 - давление и плотность в состоянии покоя. По оси y задача бесконечна; соответствующее условие
- давление и плотность в состоянии покоя. По оси y задача бесконечна; соответствующее условие
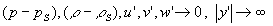 . (10)
. (10)
Кроме того, считается, что в бесконечно далеком прошлом жидкость находилась в состоянии покоя, то есть
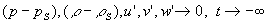 . (11)
. (11)
Условие (11) фиксирует некоторый класс чисто волновых движений жидкости, не определяя его однозначно (оно отфильтровывает стационарные течения, на фоне которых могли бы распространяться волны).
Следующий шаг состоит в моделировании длинных волн Кельвина. Более точно, из всего многообразного класса возможных движений жидкости нужно выделить именно тот режим, который соответствует длинным волнам Кельвина. Это достигается введением характерных масштабов переменных состояния и характерных масштабов изменения этих переменных в пространстве-времени. Основой для введения масштабов служат соотношения, возникающие в линейной теории волн Кельвина в “традиционном приближении”. Характерные масштабы d
x, d
y, d
z и d
t пространственных и временных изменений переменных состояния (избыточного давления, избыточной плотности и скорости жидкости) в волне Кельвина связаны соотношениями 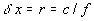 ,
, 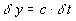 (см., напр., [7]). Здесь r – внутренний радиус деформации Россби,
(см., напр., [7]). Здесь r – внутренний радиус деформации Россби, 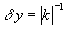 - масштаб изменений по оси y, k – характерное волновое число, фазовая скорость c определяется из решения краевой задачи по z [7]. Пусть d
N – характерное значение частоты Брента-Вяйсяля, d
c – характерное значение скорости волны, тогда
- масштаб изменений по оси y, k – характерное волновое число, фазовая скорость c определяется из решения краевой задачи по z [7]. Пусть d
N – характерное значение частоты Брента-Вяйсяля, d
c – характерное значение скорости волны, тогда 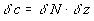 . Характерная величина избыточного давления в волне Кельвина определяется как
. Характерная величина избыточного давления в волне Кельвина определяется как
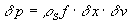 , (12)
, (12)
избыточной плотности – как 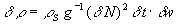 . (13)
. (13)
Здесь d
u, d
v, d
w – характерные масштабы компонент скорости (во избежание недоразумений отметим, что уравнения традиционного приближения инвариантны относительно вращений в плоскости (x, y)). Из уравнения непрерывности для крупномасштабных движений следует, что
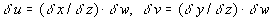 . (14)
. (14)
Безразмерные переменные определяются как
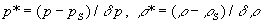 ,
,
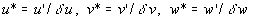 , (15)
, (15)
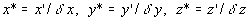 `
`
В новых переменных система уравнений движения примет вид
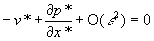 ,
,
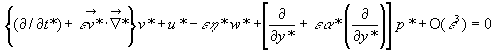 ,
,
 , (16)
, (16)
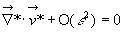 ,
,
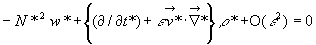 ,
,
где N* = (N / d
N) – безразмерная частота Брента-Вяйсяля, и введен параметр h
* = [f / (e
d
N)] ctgj
sing
. Параметр 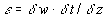 (17)
(17)
характеризует степень нелинейности волны; далее предполагается, что e
<< 1 (в противном случае введение масштабов процесса на основе линейной теории окажется несостоятельным). При получении уравнений предполагалось, что для многих реальных ситуаций эти соотношения выполняются.
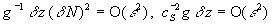 ;
;
Для решения системы (16) применяется редуктивная теория возмущений [8]. Для избыточного давления и других переменных состояния используется разложение в ряд по степеням малого параметра e
в форме
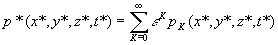 . (18)
. (18)
Если разложения вида (18) подставить в (16) и коэффициенты при каждой степени e
приравнять к нулю, то в порядке e
0 получается система уравнений (для краткости ниже опущены звездочки у безразмерных независимых переменных и безразмерных параметров)
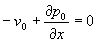 ,
, 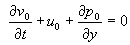 ,
, 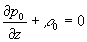 ,
,
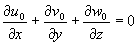 ,
, 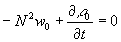 . (19)
. (19)
Чтобы избавиться от секулярных членов, возникающих в порядке O
(e
), вводится медленное время (см., напр., [9])
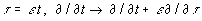 . (20)
. (20)
Граничные условия (6), (8)-(11) приводят к требованиям
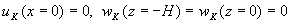 , (21)
, (21)
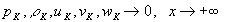 , (22)
, (22)
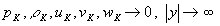 , (23)
, (23)
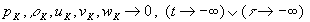 . (24)
. (24)
После замены (20) в порядке O
(e
) возникнет следующая система уравнений:
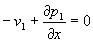 ,
, 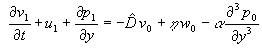 ,
,
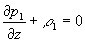
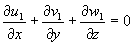 ,
,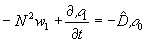 . (25)
. (25)
где введен дифференциальный оператор
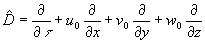 . (26)
. (26)
Решение системы (19), удовлетворяющее граничным условиям, и ищется в виде
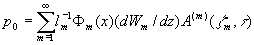 ,
, 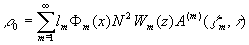 ,
,
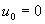 , (27)
, (27)
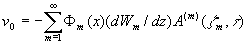 ,
, 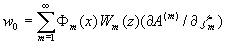 .
.
Здесь 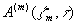 - неизвестная пока амплитудная функция переменной
- неизвестная пока амплитудная функция переменной
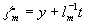 (28)
(28)
и медленного времени t
, 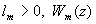 - собственные значения и собственные функции краевой задачи
- собственные значения и собственные функции краевой задачи
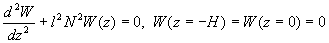 , (29)
, (29)
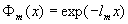 .
.
Решая систему уравнений (25) с требованиями (21)-(24), как условие отсутствия секулярных членов получаем систему интегро-дифференциальных уравнений на амплитуды
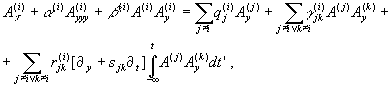 (30)
(30)
где в левой части стоит обычный нелинейный оператор Кортевега-де Фриза, а правая часть описывает взаимодействие мод. В формуле (30) для краткости введено обозначение
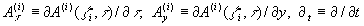 .
.
Предварительное исследование данной системы в случае двух возбужденных мод показывает, что при определенных условиях в модах могут распространяться солитоноподобные метастабильные образования. Их взаимное влияние сводится к перенормировке скоростей и малым вариациям формы. При этом, как следует из расчетов, возможна ситуация, когда разность скоростей мод уменьшается. По нашему мнению, на этом пути можно достичь понимания таких обнаруженных в эксперименте явлений, как переключение возбуждения с одной группы мод на другую в теле проходящей волны.
Литература
- Chensky A.G., Lovtsov S.V., Parfenov Yu.V., Rastegin A.E., Rubtzov V.Yu. On the coastal-trapped waves in the southern area of lake Baikal // “Oceanic Fronts and Related Phenomena”, Konstantin Fedorov Memorial Symposium. St.-Petersburg: RSHMU Publishers, 1998. P. 29-30.
- Ловцов С.В., Парфенов Ю.В., Растегин А.Э., Рубцов В.Ю., Ченский А.Г. Крупномасштабные возмущения температуры и внутренние волны в озере Байкал // “Астрофизика и физика микромира”, Материалы Байкальской школы по фундаментальной физике. Иркутск: Изд-во Иркут. Ун-та, 1998. С. 279-285.
- Segur H., Hammak J.L. Soliton models of long internal waves // J. Fluid Mech. 1982. 118. P. 285-304.
- Redekopp L.G. On the theory of solitary Rossby waves // J. Fluid Mech. 1977. 82. P. 725-745.
- Smith R. Nonlinear Kelvin and continental shelf waves // J. Fluid Mech. 1972. 52. P. 379-391.
- Farmer D. M. Observation of Long Nonlinear Internal Waves in a Lake // J. Phys. Oceanogr. 1978. V. 8. P. 63-73.
- Ле Блон П., Майсек Л. Волны в океане. М.: Мир, 1981. Ч. 1. 480 с.
- Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М.: Мир, 1988. 694 с.
- Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987. 479 с.

