|
|
 |
 |

|
| |
ИССЛЕДОВАНИЕ АТМОСФЕРЫ МЕТОДОМ ЛАЗЕРНОГО ПОЛЯРИЗАЦИОННОГО ЗОНДИРОВАНИЯ
И.В. Cамохвалов
Томский государственный университет
Введение
Природа электромагнитного излучения обязывает описывать процессы рассеяния света в векторной форме. Тем не менее, в большинстве работ по лазерному зондированию аэрозолей используется уравнение лазерной локации в скалярном приближении. Практика оптических исследований показала оправданность этого представления для большей части атмосферных аэрозолей. Но существует значимый класс естественных аэрозолей, а именно кристаллические облака, для которых скалярное приближение уравнения лазерной локации оказывается недостаточным, и описание процесса рассеяния должно проводиться в векторной форме. К этому побуждает сильно выраженная анизометрия частиц и их, в той или иной мере, упорядоченное положение в пространстве. Основным ориентирующим фактором является совместное действие гравитации и аэродинамических сил, приводящих, как известно, к ориентации частиц с большими диаметрами преимущественно в горизонтальной плоскости. Но и в этой плоскости, как будет показано ниже, существуют выделенные направления, обусловленные, возможно, действием электростатических сил, вдоль которых могут ориентироваться оси вытянутых частиц. Несферичность и ориентация частиц приводят к выраженной анизотропии рассеяния света, которая в отдельных случаях проявляется в виде известных аномальных оптических явлений (ложные Солнца, столбы и т.д.).
Эффекты, связанные с анизотропией рассеяния в кристаллических ансамблях, необходимо учитывать при оценке влияния облачности верхнего яруса на работу оптических средств связи и локации на трассах Земля-космос, дистанционных средств зондирования, установленных на спутниках, и в расчетах поля рассеянной радиации. Лидарные измерения поляризационных характеристик кристаллической облачности дают экспериментальную основу для подобного учета, так как позволяют оперативно получать сведения о форме и ориентации частиц. Они оказываются также полезным инструментом для исследования влияния геофизических полей на характеристики аэрозольного светорассеяния, как, например, в [1], где исследовалось влияние электрического поля.
1. Описание поляризационных свойств лазерного излучения и характеристик среды
1-1. Вектор-параметр Стокса. Электрический вектор электромагнитного поля 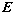 , возникающего при рассеянии плоской волны на оптической неоднородности, в дальней зоне описывается линейной векторной функцией от электрического вектора падающей волны , возникающего при рассеянии плоской волны на оптической неоднородности, в дальней зоне описывается линейной векторной функцией от электрического вектора падающей волны 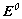 [2]: [2]:
|
 . .
|
(1) |
Здесь  и и 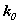 - волновые векторы соответственно рассеянной и падающей волн, распространяющихся в направлении - волновые векторы соответственно рассеянной и падающей волн, распространяющихся в направлении 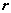 и и 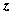 , соответственно. Векторы , соответственно. Векторы 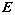 и и 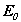 записываются каждый в своей системе координат, которые связаны с плоскостью, содержащей направления k и k0 , “плоскостью референции”, таким образом, что оси x и x0 перпендикулярны этой плоскости, а y и y0 лежат в ней, причем записываются каждый в своей системе координат, которые связаны с плоскостью, содержащей направления k и k0 , “плоскостью референции”, таким образом, что оси x и x0 перпендикулярны этой плоскости, а y и y0 лежат в ней, причем  , , 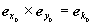 . Элементы матрицы A представляют собой безразмерные комплексные амплитуды рассеяния и зависят от угла рассеяния . Элементы матрицы A представляют собой безразмерные комплексные амплитуды рассеяния и зависят от угла рассеяния 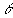 и азимутального угла и азимутального угла 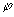 . Заметим, что угол рассеяния лежит в плоскости референции. . Заметим, что угол рассеяния лежит в плоскости референции.
Детекторы оптического излучения реагируют на интенсивность. Поэтому поляризационные характеристики световых пучков удобнее выражать через четырехмерный вектор Стокса, компоненты которого представляют собой линейные комбинации элементов матрицы когерентности
|
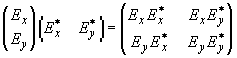 , ,
|
(2) |
где звездочки означают комплексное сопряжение.
Параметры Стокса определяются следующими соотношениями:
где  - фазовый сдвиг между компонентами поля. - фазовый сдвиг между компонентами поля.
Из (3) видно, что параметры I и Q есть сумма и разность интенсивностей двух взаимно ортогональных компонентов электромагнитного поля. Параметр U есть разность интенсивностей двух ортогональных компонентов, измеренных в системе координат, повернутой на 450 относительно исходной
|
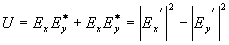 . .
|
|
Для измерения параметра V нужно измерять интенсивности взаимно ортогональных компонентов пучка, на пути которого помещена четвертьволновая пластинка, быстрая ось которой установлена под углом 450 по отношению к оси x. (Поворот осуществляется против часовой стрелки, если смотреть навстречу пучку). Из соотношений (3) следует процедура измерения параметров Стокса, которая реализуется в поляризационном лидаре [1].
1-2. Матрица рассеяния.
При переходе от описания процесса рассеяния в терминах напряженностей поля к интенсивностям, уравнение (1) заменяется уравнением
|
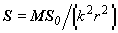 , ,
|
(4) |
где S и S0 - векторы-столбцы с компонентами, определенными соотношениями (3), а M - 4 х 4 матрица Мюллера для рассеяния в направлении, определяемом углом рассеяния 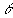 и азимутальным углом и азимутальным углом 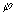 . В дальнейшем мы будем ее называть матрицей рассеяния света (МРС). . В дальнейшем мы будем ее называть матрицей рассеяния света (МРС).
Элементы МРС mij / k2 имеют размерность площади и физический смысл дифференциального сечения рассеяния. Сечения независимых рассеивателей складываются. Просуммированные сечения, отнесенные к величине рассеивающего объема, дают коэффициент объемного направленного светорассеяния. Именно в таком смысле мы будем в дальнейшем понимать элементы МРС, опуская множитель 1 / k2 в уравнении (4).
1-3. Матрица обратного рассеяния света (МОРС) пространственно ориентированных ледяных кристаллов.
Для матрицы амплитуд рассеяния произвольной частицы при рассеянии строго назад имеет место теорема A3 + A4 = 0 [2]. Следствием этой теоремы являются следующие соотношения для недиагональных элементов МОРС
|
mij = mji , если i или j 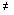 3, 3,
mij = -mji , если i или j = 3. |
(5) |
Эти соотношения не зависят от ориентации поляризационного базиса, в котором производятся измерения, и сохраняются при преобразовании
|
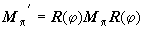 , ,
|
(6) |
где оператор поворота плоскости референции 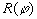 определен матрицей: определен матрицей:
|
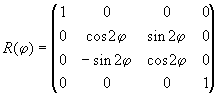 . .
|
(7) |
Это свойство МОРС сокращает число независимых элементов матрицы с 16-и до 10-и. Еще более простой вид имеет МОРС для гексагональных пластин и столбиков, часто встречающихся в кристаллических облаках, имеющих осевую и зеркальную симметрии.
Известно [2- 4], что МОРС такой частицы, если рассеяние рассматривается в системе координат, выбранной так, что ось частицы лежит в плоскости референции (азимутальный угол 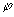 = 0) , имеет следующий вид: = 0) , имеет следующий вид:
|
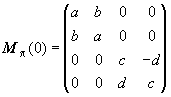 . .
|
(8) |
Элементы a, b, c, d зависят от формы, размеров и показателя преломления, но не зависят от угла 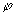 . В системе координат, повернутой вокруг направления распространения на угол . В системе координат, повернутой вокруг направления распространения на угол  , элементы МОРС преобразуются в соответствии с (6), и матрица принимает вид: , элементы МОРС преобразуются в соответствии с (6), и матрица принимает вид:
|

|
(9) |
Заметим, что диагональные элементы m22 и m33 можно преобразовать к виду
|
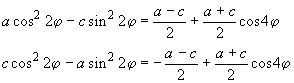 . .
|
(10) |
Матрица (9) имеет смысл МОРС единицы объема, содержащего одну частицу. Если в единичном объеме содержится N частиц, то их МОРС должны быть просуммированы.
Матрица обратного рассеяния для ансамбля полидисперсных и полиориентированных частиц получена в работе [5] и имеет следующий вид:
|
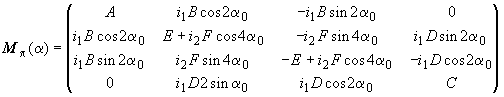 , ,
|
(11) |
где A, B, C, D, E, F - производные соответственно от a, b, c, d, (a-c)/2, (a+c)/2 величины вида:
|
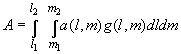 , ,
|
(12) |
где g(l,m) - функция распределения по максимальному l и минимальному m диаметрам частиц.
|
 . .
|
(13) |
Угол 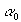 имеет смысл азимутального положения моды распределения Мизеса относительно плоскости референции ( имеет смысл азимутального положения моды распределения Мизеса относительно плоскости референции (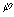 = 0) [5]. Распределение имеет вид: = 0) [5]. Распределение имеет вид:
|
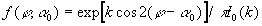 , ,
|
(14) |
где I0(k)-модифицированная функция Бесселя первого рода нулевого порядка.
Степень концентрации возле направления 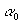 зависит от параметра k: чем он больше, тем острее распределение. При k=0 распределение Мизеса переходит в равномерное распределение (Коши), при котором отсутствует выделенное направление. В матрице (11) зависит от параметра k: чем он больше, тем острее распределение. При k=0 распределение Мизеса переходит в равномерное распределение (Коши), при котором отсутствует выделенное направление. В матрице (11)
|
i1 = I1(k) / I0(k) ; i2 = I2(k) / I0(k), |
(15) |
где I0 , I1 , I2 - модифицированные функции Бесселя первого рода нулевого, первого и второго порядка. При 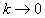  ; ; 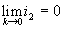 , и МОРС (11) принимает вид диагональной матрицы, т.е. выделенное направление ориентации осей частиц по азимутальному углу , и МОРС (11) принимает вид диагональной матрицы, т.е. выделенное направление ориентации осей частиц по азимутальному углу 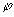 отсутствует. Приведенные выше свойства МОРС ансамбля осесимметричных частиц являются теоретической основой методики определения состояния ориентированности частиц. отсутствует. Приведенные выше свойства МОРС ансамбля осесимметричных частиц являются теоретической основой методики определения состояния ориентированности частиц.
2. Уравнение лазерного зондирования в векторной форме
2-1. Однократное рассеяние. Уравнение лазерной локации, записанное для мощности принимаемого рассеянного излучения, легко обобщается на вектор-параметр Стокса. Уравнение (4) после нормировок, оговоренных выше, определяет вектор Стокса излучения, рассеянного единицей объема в единицу телесного угла в заданном направлении. Вектор Стокса излучения, рассеянного объемом  V, запишем в следующем виде: V, запишем в следующем виде:
|
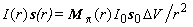 , ,
|
(16) |
где I0 , I - интенсивности (первые параметры Стокса) падающего и рассеянного излучения, а s0 и s - безразмерные векторы
|
s(r)= (1, q(r), u(r), v(r))t , s0 = (1, q0 , u0 , v0 )t, |
(17) |
имеющие смысл нормированных на интенсивность векторов Стокса. Индекс 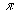 у матрицы рассеяния означает, что рассматривается рассеяние назад. В лазерном зондировании на детектор приемника в момент t поступает излучение из объема у матрицы рассеяния означает, что рассматривается рассеяние назад. В лазерном зондировании на детектор приемника в момент t поступает излучение из объема
|
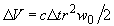 , ,
|
(18) |
где c - скорость света; 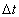 - длительность лазерного импульса; w0 - телесный угол, в котором распространяется лазерное излучение. Произведение r2w0 имеет смысл освещаемой площади. Интенсивность лазерного излучения, падающего на объем - длительность лазерного импульса; w0 - телесный угол, в котором распространяется лазерное излучение. Произведение r2w0 имеет смысл освещаемой площади. Интенсивность лазерного излучения, падающего на объем 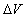 , равна , равна
|
I0 (r)= P0 T(r)/ r2w0, |
(19) |
где P0 - мощность излучения лазера; T(r) - пропускание трассы от лидара до объема.
Мощность падающего на антенну рассеянного излучения равна:
где A - площадь антенны.
Реакция фотодетектора пропорциональна световой энергии, поступившей на него за некоторое время 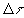 , которое либо определяется инерционностью прибора, либо задается экспериментатором. Назовем лидарным откликом величину , которое либо определяется инерционностью прибора, либо задается экспериментатором. Назовем лидарным откликом величину
|
 , ,
|
(21) |
где 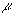 - коэффициент пропорциональности между световой энергией и реакцией детектора; - коэффициент пропорциональности между световой энергией и реакцией детектора; 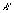 - коэффициент оптических потерь на элементах приемного тракта. - коэффициент оптических потерь на элементах приемного тракта.
Объединяя (16) - (21), получим
|
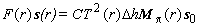 , ,
|
(22) |
где C - аппаратная константа лидара; 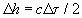 - пространственная длительность, соответствующая времени интегрирования - пространственная длительность, соответствующая времени интегрирования  ; ; 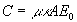 ; ; 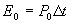 - мощность импульса. - мощность импульса.
Уравнение (22) является векторным аналогом скалярного лидарного уравнения, записанного для мощности рассеянного излучения.
2-2. Учет второй кратности рассеяния
Лидарный сигнал можно представить в виде суммы сигналов, обусловленных однократным и двукратным рассеянием
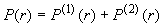 . .
В силу аддитивности вектор Стокса суммарного сигнала
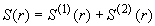 . .
Для моностатического лидара вектор Стокса двукратно рассеянного назад излучения определяется как [6]
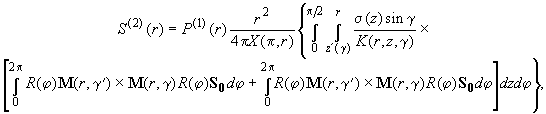
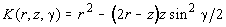 , , 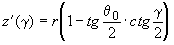 . .
Здесь Р(1)(r) - мощность эхо-сигнала однократного рассеяния; X(p
,r) - индикатриса рассеяния в направлении назад; s
(r) - объемный коэффициент рассеяния; q
0- угол поля зрения; g
- угол рассеяния.
3. Методика измерения морс поляризационным лидаром
3-1. Характеристики высотного лидара “СТРАТОСФЕРА”
Лидар построен по моностатической схеме с разнесенными оптическими осями приемной и передающей антенн. Для уменьшения засветок фотодетекторов из ближней зоны база между осями составляет 1,2 м. Приемной антенной служит зеркальный объектив, выполненный по схеме Кассегрена, с диаметром главного зеркала 500 мм. Эффективное фокусное расстояние объектива 5700 мм. На оптической оси в фокальной плоскости помещена диафрагма диаметром 5 мм, ограничивающая угловой раскрыв антенны до величины 0,9 мрад. Передающая антенна представляет собой линзовый коллиматор 10´
, уменьшающий расходимость лазерного пучка до величины 0,5 мрад. В качестве передатчика используется YAG:Nd- лазер с удвоением частоты.
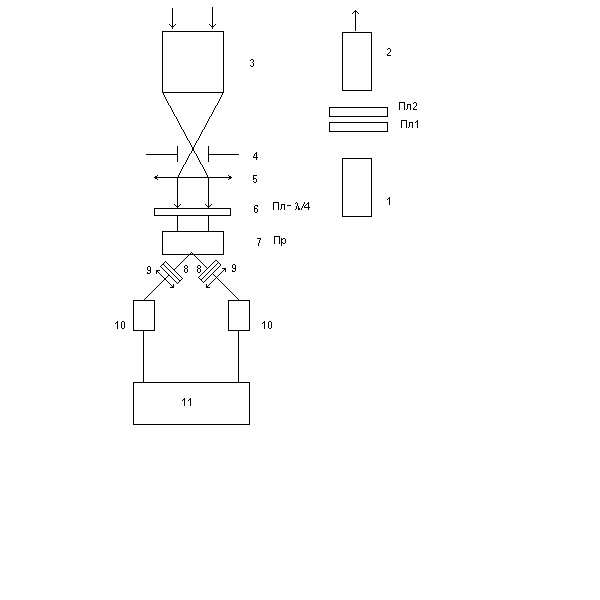
На оптической оси лазера 1 (рис.1) установлены две l
/
4 пластинки, поворачивающиеся вокруг оптической оси на заданный угол. Пройдя пластинки и коллиматор 2, излучение уходит в атмосферу.
|
Рассеянное излучение, поступив на объектив 3, проходит последовательно диафрагму поля зрения 4, линзу 5, трансформирующую расходящийся пучок в квазипараллельный. Далее он попадает на узел трансформации состояния поляризации рассеянного излучения, содержащий четвертьволновую пластинку 6 и призму Волластона 7, которые могут поворачиваться вокруг оптической оси. Из призмы выходят два пучка с ортогональными линейными поляризациями, проходящие через интерференционные фильтры 8, и линзами 9 собираются на катоды фотоумножителей. |
|
Поток фотоимпульсов поступает на двухканальную систему счета фотонов, разносящую импульсы по временным стробам так, что временное положение строба определяет дистанцию до рассеивающего объема. Система регистрации, отображения и первичной обработки данных принципиально не отличается от аналогичных устройств других лидаров. Минимальная длительность строба 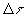 = 80 нс, что соответствует разрешению по дальности = 80 нс, что соответствует разрешению по дальности  =12м. Максимальная частота счета 50 Мгц. Основные технические характеристики лидара приведены в таблице 1. =12м. Максимальная частота счета 50 Мгц. Основные технические характеристики лидара приведены в таблице 1.
Отличительной особенностью поляризационного лидара “Стратосфеа-1М” является наличие в нем узла трансформации состояния поляризации излучения передатчика, что делает возможным измерения МОРС. Измерения должны быть отнесены к некоторой системе координат, которую естественно определить таким образом, чтобы описание поляризационных характеристик было, по возможности, простым. В описываемом лидаре система координат определена следующим образом.
Таблица 1.
|
Передатчик |
Приемник |
|
Тип лазера |
ЛТИ-405 |
Тип антенны Телескоп Кассегрена |
|
Рабочая длина волны излучения, нм |
532 |
Диаметр антенны, м |
0.5 |
|
Энергия импульса, мДж |
до 40 |
Фокусное расстояние, м |
5.7 |
|
Длительность импульса, нс |
12 |
Угол поля зрения, угл. Мин |
3 |
|
Частота повтрения импульсов, Гц |
12-25 |
Спектральная полушир. пропускания |
|
Расходимость излучения после |
|
интерференционных фильтров, нм |
1,5 |
|
коллимации, угл. мин |
1,5 |
Поляризационные элементы: |
|
|
Поляризация излучения: |
|
призма Волластона
|
|
начальная линейная |
(1 1 0 0) |
пластина l
/
4
|
|
после узла трансформации: |
|
Детекторы: |
|
|
линейная |
(1 -1 0 0) |
два фотоумножителя ФЭУ-130
|
|
линейная |
(1 0 1 0) |
Регистрация: счетчики фотонов с макси |
|
круговая |
(1 0 0 1) |
мальной скоростью счета, МГц |
50 |
|
Узел трансформации - две пластины l
/
4 |
Компьютер |
IBM |
Оси z0 и z имеют естественные направления волновых векторов посылаемого и принимаемого излучения. Вторым естественным репером является плоскость, в которой происходят колебания электрического вектора линейно поляризованного лазерного излучения. В этой плоскости, содержащей z0, определяется ось x0 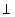 z0. В перпендикулярной к ней плоскости, также содержащей z0, определяется ось y0. Положительные направления осей выбираются так, чтобы единичные векторы образовали правовинтовую тройку z0. В перпендикулярной к ней плоскости, также содержащей z0, определяется ось y0. Положительные направления осей выбираются так, чтобы единичные векторы образовали правовинтовую тройку 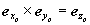 . В системе x0 , y0 , z0 измеряются параметры Стокса посылаемого лазерного пучка. Ось x системы координат x , y , z , в которой измеряются параметры Стокса рассеянного излучения, выбирается параллельной направлению оси x0 . В системе x0 , y0 , z0 измеряются параметры Стокса посылаемого лазерного пучка. Ось x системы координат x , y , z , в которой измеряются параметры Стокса рассеянного излучения, выбирается параллельной направлению оси x0 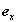 коллинеарен коллинеарен 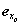 . .
Призма Волластона устанавливается так, чтобы нормаль к плоскости, в которой происходит разведение пучков, совпадала с направлением 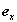 . Ось y определяется в этой плоскости также условием . Ось y определяется в этой плоскости также условием 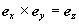 . При таком выборе системы координат один из выходящих из призмы пучков равен x-составляющей, а другой, соответственно, y-составляющей интенсивности падающего на призму пучка. . При таком выборе системы координат один из выходящих из призмы пучков равен x-составляющей, а другой, соответственно, y-составляющей интенсивности падающего на призму пучка.
Прохождение пучка излучения через призму Волластона и четвертьволновую пластинку в приемном канале можно описать как последовательное действие операторов фазовой пластинки N(q
) и линейного поляризатора L(q
) на вектор Стокса пучка S(r). Угол поворота q
плоскости пропускания поляризатора и быстрой оси фазовой пластинки отсчитывается от оси x базиса против часовой стрелки. Поскольку в оптике непосредственному измерению доступна только интенсивность, то прохождение пучка излучения через приемный канал лидара можно охарактеризовать тремя парами приборных векторов G для соответствующих комбинаций положений призмы и фазовой пластинки:
Здесь индексы x , y означают, что действие данного вектора приводит к измерению интенсивностей компонентов поляризованных, соответственно, перпендикулярно и параллельно плоскости разведения пучков в призме Волластона. Верхние индексы означают, что действие пары векторов, обозначенных, например, индексом q , приводят к измерению параметра q безразмерного вектора Стокса s . Таким образом,
|
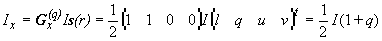 , ,
 , ,
|
|
где t - знак транспонирования. Отсюда, заметив, что Ix + Iy = I , получим q = (Ix - Iy)/(Ix + Iy).
Рассмотрим теперь действие узла трансформации состояния поляризации излучения лазера. В соответствие с принятым базисом лидара первоначальное состояние поляризации лазерного пучка описывается нормированным вектором Стокса s0 = ( 1 1 0 0 )t.
Четыре различные комбинации положений четвертьволновых пластин позволяют изменять состояние поляризации лазерного пучка без существенной потери мощности:
|
1) |
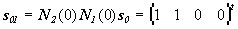 - -
|
(24) |
линейная поляризация с колебаниями E вдоль оси x базиса лидара;
|
2) |
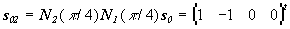 - -
|
(25) |
линейная поляризация с колебаниями вдоль оси y ;
|
3) |
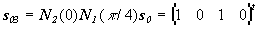 - -
|
(26) |
линейная поляризация с поворотом плоскости колебаний на 450;
|
4) |
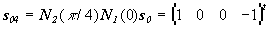 - -
|
(27) |
правая круговая поляризация.
3-2. Измерение вектора-Стокса лидарного сигнала и МОРС
Рассмотрим одно из двенадцати измерений, необходимых для определения МОРС. Пусть поляризация лазерного пучка описывается вектором Стокса s01 (24). Подставим его в уравнение локации (22) и подействуем на уравнение первой парой приборных векторов (23)
|
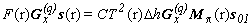 , , 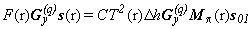
|
(28) |
Напомним, что s(r) и s01 это нормированные безразмерные векторы вида (13).
После перемножения матриц ,(28) имеет вид:
|
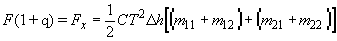 , ,
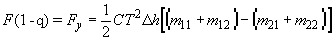 . .
|
(29) |
Для упрощения записи формул опущена зависимость от r , но, согласно(28) она подразумевается. В (29) Fx(r) и Fy(r) - приведенные реакции фотодетекторов, сумма которых пропорциональна реакции на полную интенсивность, т. е. Fx + Fy = F . Сложение и вычитание уравнений (29) дает:
|
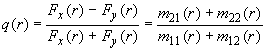 . .
|
(30) |
Применяя в (28) следующие две пары приборных векторов (23), получим
|
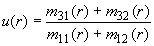 ; ; 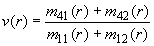 . .
|
(31) |
Здесь q(r), u(r), v(r) - нормированные параметры Стокса рассеянного излучения. Повторение подобных измерений при состояниях поляризации лазерного пучка (25)-(27) дает комбинации элементов МОРС, приведенные в таблице 2.
Таблица 2.
|
Безразмерный |
Действующая пара приборных векторов |
Определяемая комбинация |
|
вектор Стокса
лазерного пучка |
1/2(1 1 0 0)
1/2(1 -1 0 0) |
1/2(1 0 1 0)
1/2(1 0 -1 0) |
1/2(1 0 0-1)
1/2(1 0 0 1) |
элементов МОРС
i = 2, 3, 4 |
| |
Измеряемые величины |
|
|
s01 = (1 1 0 0)t |
q1 |
u1 |
v1 |
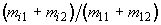
|
|
s02 = (1 -1 0 0)t |
q2 |
u2 |
v2 |
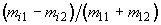
|
|
s03 = (1 0 1 0)t |
q3 |
u3 |
v3 |
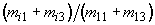 |
|
s04 = (1 0 0 -1)t |
q4 |
u4 |
v4 |
 |
Каждое измерение одной из величин q, u, v сводится к измерению реакции двух детекторов Fx и Fy. Для обеспечения одинаковой реакции детекторов на равные световые потоки проводится нормировка реакции детекторов с помощью люминесцентной таблетки, дающей неполяризованный свет, которая вводится в оптический тракт приемного канала. Поток излучения от таблетки разделяется призмой Волластона на два равных световых потока, падающих на катоды ФЭУ. Отношение сигналов дает искомый коэффициент.
Для получения абсолютных значений коэффициентов направленного светорассеяния используется калибровка по молекулярному рассеянию7-9. Определяется отношение суммарного коэффициента рассеяния к коэффициенту молекулярного рассеяния
|
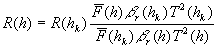 , ,
|
(32) |
где 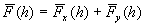 ; b
r и b
a - коэффициенты молекулярного и аэрозольного рассеяния; h - текущая высота; hk - фиксированная высота слоя, по которому проводится калибровка. ; b
r и b
a - коэффициенты молекулярного и аэрозольного рассеяния; h - текущая высота; hk - фиксированная высота слоя, по которому проводится калибровка.
4. Результаты поляризационного лазерного зондирования облаков верхнего яруса
4-1. Высотные профили составляющих вектора Стокса лидарного сигнала
Уже первые измерения векторов Стокса лидарных сигналов [10-12] показали результаты, отличные от тех, которые можно было бы предсказать основываясь на представлениях о диагональном виде МОРС атмосферных аэрозолей. В таблице 3 приведены результаты измерений вектора Стокса лидарного сигнала, приходящего из области высот 5-10 км при различных поляризациях зондирующего излучения. Состояние поляризации лидарного сигнала существенно отличается от поляризации излучения передатчика, особенно на высотах, соответствующих положению перистых облаков.
Таблица 3.
|
Вектор-параметр Стокса |
Высота |
Степень |
R-фактор |
|
зондирующего излучения S0(1,Q0,U0,V0)t |
рассеянного излучения
S(1,Q,U,V)t |
|
поляри-зации |
деполя-ризации |
|
|
(1; 0,98; 0,01; 0,01) |
5,04 |
0,99 |
0,01 |
1,03 |
|
(1; 0,89; -0,01; 0,01) |
7,06 |
0,89 |
0,06 |
2,06 |
|
(1; 0,83; -0,01; 0,01) |
7,15 |
0,83 |
0,09 |
3,01 |
|
1 |
(1; 0,92; -0,02; -0,03) |
7,44 |
0,92 |
0,04 |
2,14 |
|
1 |
(1; 0,85; -0,12; -0,01) |
7,63 |
0,85 |
0,07 |
3,62 |
|
0 |
(1; 0,82; 0,00; -0,02) |
7,92 |
0,82 |
0,10 |
7,21 |
|
0 |
(1; 0,89; 0,01; -0,02) |
8,11 |
0,89 |
0,06 |
2,24 |
|
(1; 0,95; 0,00; 0,02) |
8,21 |
0,95 |
0,03 |
1,30 |
|
(1; 0,99; 0,04; -0,02) |
9,98 |
0,99 |
0,01 |
1,04 |
|
(1; 0,98; 0,00; 0,01) |
10,56 |
0,98 |
0,01 |
1,01 |
|
(1; -0,98; 0,02; 0,02) |
5,04 |
0,98 |
0,01 |
1,06 |
|
(1; -0,90; 0,01; 0,00) |
7,06 |
0,90 |
0,05 |
1,80 |
|
(1; -0,27; 0,01; -0,02) |
7,15 |
0,27 |
0,57 |
3,83 |
|
(1; 0,17; 0,00; 0,00) |
7,25 |
0,17 |
0,71 |
13,84 |
|
1 |
(1; -0,21; 0,02; 0,01) |
7,34 |
0,21 |
0,65 |
4,15 |
|
-1 |
(1; -0,47; 0,01; 0,00) |
7,44 |
0,47 |
0,36 |
2,81 |
|
0 |
(1; -0,82; 0,02; 0,02) |
7,54 |
0,82 |
0,10 |
1,87 |
|
0 |
(1; -0,83; -0,01; 0,02) |
7,63 |
0,83 |
0,09 |
1,50 |
|
(1; 0,09; 0,03; 0,01) |
7,73 |
0,09 |
0,83 |
7,68 |
|
(1; 0,16; 0,06; 0,02) |
7,82 |
0,17 |
0,71 |
19,95 |
|
(1; 0,02; 0,03; -0,01) |
7,92 |
0,05 |
0,90 |
6,69 |
|
(1; -0,81; 0,00; 0,01) |
8,11 |
0,81 |
0,10 |
1,64 |
|
(1; -0,89; 0,03; -0,01) |
8,21 |
0,89 |
0,06 |
1,78 |
|
(1; -0,02; 0,25; -0,08) |
7,25 |
0,26 |
0,59 |
14,89 |
|
1 |
(1; -0,01; 0,12; -0,06) |
7,34 |
0,13 |
0,77 |
8,98 |
|
0 |
(1; 0,00; -0,38; -0,01) |
7,44 |
0,38 |
0,45 |
3,38 |
|
1 |
(1; 0,00; -0,21; -0,02) |
7,54 |
0,21 |
0,65 |
5,17 |
Таблица 3.(продолжение)
|
Вектор-параметр Стокса |
Высота |
Степень |
R-фактор |
|
зондирующего излучения S0(1,Q0,U0,V0)t |
рассеянного излучения
S(1,Q,U,V)t |
|
поляри-зации |
деполя-ризации |
|
|
0 |
(1; 0,02; 0,47; 0,03) |
7,63 |
0,47 |
0,36 |
26,55 |
|
(1; -0,11; 0,43; -0,04) |
7,73 |
0,45 |
0,38 |
30,46 |
|
(1; -0,08; 0,35; -0,11) |
7,92 |
0,37 |
0,46 |
11,35 |
|
(1; 0,04; 0,23; -0,08) |
8,02 |
0,24 |
0,61 |
5,46 |
|
(1; 0,03; -0,48; 0,02) |
8,21 |
0,48 |
0,35 |
2,11 |
|
(1; 0,02; -0,98; 0,03 |
9,94 |
0,98 |
0,01 |
1,07 |
|
(1; 0,02; -0,99; 0,02) |
10,51 |
0,99 |
0,01 |
1,05 |
|
(1; 0,01; 0,01; -0,99) |
5,04 |
0,99 |
0,01 |
1,09 |
|
(1; -0,02; -0,03; -0,65) |
7,06 |
0,65 |
0,21 |
4,34 |
|
1 |
(1; -0,04; -0,07; -0,57) |
7,34 |
0,59 |
0,26 |
5,77 |
|
0 |
(1; -0,03; -0,11; -0,62) |
7,44 |
0,62 |
0,38 |
5,30 |
|
0 |
(1; -0,01; -0,09; -0,61) |
7,56 |
0,62 |
0,24 |
6,26 |
|
1 |
(1; -0,02; -0,08; -0,60) |
7,63 |
0,61 |
0,25 |
10,35 |
|
(1; -0,05; -0,15; -0,54) |
7,73 |
0,56 |
0,29 |
11,42 |
|
(1; -0,09; -0,18; -0,47) |
7,82 |
0,51 |
0,32 |
8,14 |
|
(1; -0,12; -0,09; -0,51) |
8,02 |
0,56 |
0,31 |
8,95 |
|
(1; -0,14; -0,09; 0,54) |
8,11 |
0,90 |
0,28 |
4,70 |
|
(1; 0,04; -0,02; -0,90) |
8,21 |
0,93 |
0,05 |
1,83 |
|
(1; 0,04; 0,02; -0,98) |
8,40 |
0,98 |
0,06 |
2,40 |
|
(1; 0,03; 0,01; -0,99) |
9,94 |
0,99 |
0,01 |
1,04 |
|
(1; 0,02; 0,05; -0,99) |
10,51 |
0,98 |
0,01 |
1,01 |
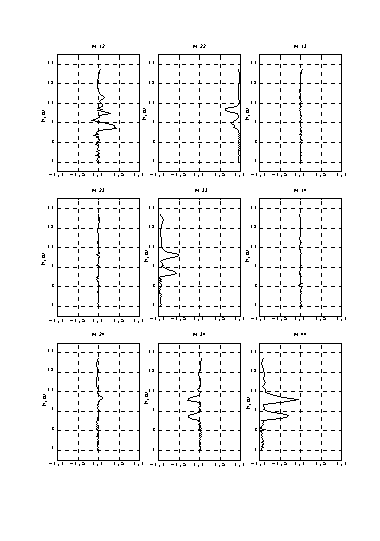
На рис.2 приведены измеренные профили элементов МОРС. Недиагональные элементы m12 и m34 в слое на высотах 8 - 9.5 км заметно отличаются от нуля. Проведенный в ИОА СО РАН в течение 1988-1990г.г. цикл измерений был обобщен в работе [13] и подтвердил ранее высказанное предположение о частом и существенном влиянии ориентированности несферических частиц на поляризационные характеристики рассеянного света. Развитие описанной выше методики измерения элементов МОРС позволило перейти от качественного анализа к количественной оценке параметров ориентированности [14-15].
4-2. Ориентация кристаллов в перистых облаках
Наиболее важным результатом исследований последних лет явилось экспериментальное доказательство факта частого проявления состояния ориентированности частиц кристаллической облачности, обусловленного факторами, отличными от известного аэродинамического ориентирования при падении в поле силы тяжести. В последнем случае вертикаль является направлением, вдоль которого происходит преимущественное ориентирование нормалей к поверхностям пластинчатых кристаллов или вокруг которого равномерно распределяются оси вытянутых частиц. Поскольку зондирование производилось по направлению в зенит, то, опираясь на модель МОРС вида (25) для ансамблей частиц, ориентированных только падением, можно было бы предсказать нулевые значения недиагональных элементов МОРС. Но, как оказалось, более чем в 30% случаев измерений МОРС эти элементы отличны от нуля, что в рамках принятой модели означает либо преимущественный наклон пластинчатых кристаллов, либо ориентацию осей вытянутых частиц. Иными словами, и в том и в другом случае имеется некоторая выделенная вертикальная плоскость, возле которой группируются оси симметрии частиц. Эксперименты показали, что в кристаллических облаках параметр i2 , который согласно (25) можно найти из экспериментальной МОРС по формулам
лежит в пределах от 0 до 0,3 , редко незначительно превышая эту величину. Согласно определению (28), значение i2 = 0,3 примерно соответствует k = 2 в распределении (27). Этот случай представлен на рис.3.
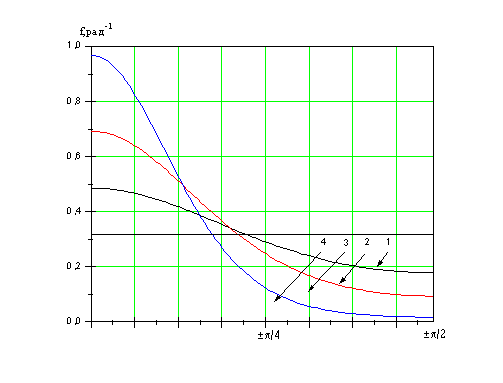
Рис.3.Распределение Мизеса 1-k=0; I0(0)=1; 2-k=0.5; 3-k=1; 4-k=2.
Сравнив с распределением Коши можно видеть, что вблизи моды вероятность нахождения оси частицы в интервале углов 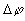 более чем в три раза превышает вероятность равномерного распределения, а вблизи углов более чем в три раза превышает вероятность равномерного распределения, а вблизи углов  почти на порядок меньше. Асимметрия расположения осей частиц заметная, что должно сказываться на поляризационных характеристиках не только обратного, но и общего рассеяния. Пространственное положение моды распределения, то есть направление преимущественной ориентации в большинстве случаев близко к широтному. почти на порядок меньше. Асимметрия расположения осей частиц заметная, что должно сказываться на поляризационных характеристиках не только обратного, но и общего рассеяния. Пространственное положение моды распределения, то есть направление преимущественной ориентации в большинстве случаев близко к широтному.
Посредством измерений МОРС были получены интересные результаты при наблюдении эволюции аэрозольного слоя, возникшего после извержения вулкана Пенатубо [14]. Первоначально наблюдавшийся в июле 1991г. слой давал увеличение отношения рассеяния R(h) на высотах от 13,5 до 16,5 км в виде двугорбого распределения с провалом на высоте около 15 км. Значение R(h) в максимумах было от 2 до 2,5. Нормированная МОРС имела диагональный вид при абсолютных значениях 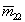 , , 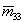 и и 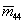 , равных 0,95-0,97. Такой вид МОРС сохранялся в течение августа и сентября того же 1991г. Это допускает два толкования. Слой состоял либо из капель, либо из настолько мелких частиц, что рассеяние на них было релеевским. И в том, и в другом случае это наводит на мысль об образовании слоя путем конденсации из газовой фазы. Наблюдения в октябре показали, что на высотах от 10 до 15км существует аэрозольный слой с теми же параметрами МОРС, но менее выраженный по амплитуде так, что R(h) не превышало полутора. На высоте 9,5 км обнаруживался тонкий слой толщиной 0,7 км, в котором отношение рассеяния R=7, а МОРС имела следующий вид , равных 0,95-0,97. Такой вид МОРС сохранялся в течение августа и сентября того же 1991г. Это допускает два толкования. Слой состоял либо из капель, либо из настолько мелких частиц, что рассеяние на них было релеевским. И в том, и в другом случае это наводит на мысль об образовании слоя путем конденсации из газовой фазы. Наблюдения в октябре показали, что на высотах от 10 до 15км существует аэрозольный слой с теми же параметрами МОРС, но менее выраженный по амплитуде так, что R(h) не превышало полутора. На высоте 9,5 км обнаруживался тонкий слой толщиной 0,7 км, в котором отношение рассеяния R=7, а МОРС имела следующий вид
|
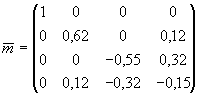
|
(34) |
Особенность этой МОРС состоит в наличии ненулевых элементов 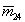 , , 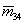 при нулевых значениях при нулевых значениях 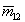 и и 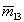 , что не может быть объяснено в рамках модели осесимметричных частиц. В то же время слой цирусов на высоте 7,5 км давал МОРС, вполне описываемую этой моделью. Анализ, проведенный в [14], позволил выдвинуть гипотезу о неводном происхождении слоя, представленного МОРС (34), и предположить сульфат аммония как наиболее вероятный материал частиц. , что не может быть объяснено в рамках модели осесимметричных частиц. В то же время слой цирусов на высоте 7,5 км давал МОРС, вполне описываемую этой моделью. Анализ, проведенный в [14], позволил выдвинуть гипотезу о неводном происхождении слоя, представленного МОРС (34), и предположить сульфат аммония как наиболее вероятный материал частиц.
Заключение
Возможности метода поляризационного зондирования в исследовании атмосферы несомненно могут быть увеличены по мере разработки теории рассеяния света на несферических и оптически анизотропных частицах при одновременном увеличении точности и оперативности измерений. Для этого имеются методические и технические предпосылки. Создание лидара, посредством которого полный цикл измерения МОРС укладывался бы в отрезок времени порядка десятка секунд, представляется осуществимым. Такой лидар мог бы быть использован для оперативной оценки качества атмосферного канала при передаче поляризационных характеристик оптических сигналов, исследованиях облачности и физических полей, ответственных за ориентацию естественных или искусственных аэрозольных трассеров в тропосфере и стратосфере.
Литература
- Донченко В.А., Кабанов М.В., Кауль Б.В., Кулаков Ю.М. Влияние постоянного электрического поля на обратное рассеяние света аэрозольными частицами NaCl и морской соли.// Изв. АН СССР, сер. ФАО, 1985, т.21, N 11, с.1173-1180.
- Ван де Хюлст Г. Рассеяние света малыми частицами. М.: ИЛ, 1961. 536 с.
- Потехин В.А.,Татаринов В.Н.Теория когерентности электромагнитного поля. М.: Связь,1978.208 с.
- Любовцева Ю.С., Моисеенко Г.С., Плахина И.Н. // Изв. АН СССР, сер. ФАО, 1976, т.12, N 5, с.506-514.
- Ромашов Д.Н., Рахимов Р.Ф. Определение ориентации осесимметричных вытянутых частиц по данным поляризационного зондирования. // Оптика атмосферы и океана. 1993. Т.6, N 8, с.891-898.
- Самохвалов И.В. Влияние двукратного рассения на поляризацинные характеристики эхо-сигналов при лазерном зондировании облаков. //Физика атмосферы и океана. 1980. Т.16, N 6, с.591-600.
- Russel Ph., Swissler T., McCormick M.P. Methodology of error analysis and simulation of lidar aerosol measurements// Appl. Optics 1979, v.18, No 22. P. 3783-3797.
- Кауль Б.В., Краснов О.А., Кузнецов А.Л. Восстановление профиля коэффициента ослабления излучения по результатам лазерного зондирования// Изв. АН СССР, сер. ФАО, 1988, т.24, N 8, с.824-828.
- Klett J.D. Lidar inversion with variable backscatter/extinction ratios// Appl. Opt. 1985, v.24, No 11. P. 1638-1643.
- Кауль Б.В., Кузнецов А.Л., Половцева Е.Р., Самохвалов И.В. Исследование кристаллических облаков на основе локационных измерений матриц обратного рассеяния света// Оптика атмосферы и океана. 1993, т.6, N 4, с.423-430.
- Zuev V.E., Kaul B.V., Kozlov N.V., Samokhvalov I.V. Lidar Studies of Light Scattering by Nonspherical Particles in the Upper Atmosphere// 9-th International Laser Radar Conf. Abst. Munich, July 1979, FRG.
- Houston J.D., Carswell A.I. Four-component polarization measurement of lidar atmospheric scattering// Appl. Optics 1978, v.17, No 4, pp. 614-620.
- Кауль Б.В, Краснов О.А., Кузнецов А.Л., Самохвалов И.В. Поляризационное зондирование аэрозольных образований верхнего яруса// Оптика атмосферы и океана. 1991, т.4, N 4, с.394-403.
- Кауль Б.В., Кузнецов А.Л., Самохвалов И.В. Проявление анизотропии рассеяния света в аэрозольных слоях стратосферы// Оптика атмосферы и океана. 1993, т.7, N 1, с.11-17.
- Кауль Б. В., Ромашов Д. Н., Самохвалов И. В. Сравнение экспериментальных и расчетных матриц обратного рассения кристаллических облаков. //Оптика атмосферы и океана. 1997. Т. 10. N10, c.1115-1121.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

