CЛУЧАЙНЫЕ
БЛУЖДАНИЯ НА ФРАКТАЛЯХ И МЕТОД ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ДРОБНОГО
ПОРЯДКА
В.Е. Архинчеев
Бурятский научный центр СО РАН
1. Введение
Исследование свойств сильно неоднородных, неупорядоченных и некристаллических аморфных материалов обусловлено, по крайней мере, двумя причинами. Необходимость более глубокого понимания физических процессов, происходящих в средах с высокой степенью неоднородности связана с широким и все возрастающим применением этих материалов в микроэлектронике и других областях. В качестве примера укажем проблему “low-K” диэлектриков : повышение быстродействия интегральных схем за счет использования диэлектриков с малой проницаемостью К. Это достигается путем применения пористых диэлектриков.
Второй причиной, вызывающий интерес к исследованию подобных материалов, является как необычность физических процессов, протекающих в них, так и недостаточность качественного понимания и количественного описания в отличие от классической физики кристаллических твердых тел. Многие представления традиционной физики твердого тела нельзя непосредственно применять для описания неупорядоченных и аморфных материалов, поскольку последние не обладают трансляционной симметрией.
Успехи качественного понимания процессов переноса в случайно неоднородных средах: от движения электрона в случайном потенциале до исследования макроскопических характеристик – диффузии, проводимости, просачивание и фильтрация воды связаны с теорией протекания (percolation) [1] и интенсивно развиваемыми в последнее время фрактальными представлениями [2]. Теория протекания адекватно описывает системы с геометрическим фазовым переходом по связности. Иначе говоря, большой класс явлений, для которых связность играет определяющую роль, можно изучать методами теории протекания. Основные задачи теории протекания просто формулируются, наглядны и легко моделируются на ЭВМ. Поэтому на протяжении многих лет существует устойчивый интерес к теории протекания. Согласно современным представлениям перколяционные кластеры на пороге протекания являются случайными статистическими фракталями [3], т.е. заполняют евклидово пространство самоподобным образом.
1.1.Фрактальная и топологическая размерности.
Впервые понятие фракталя в физике возникло в задаче об определении длины береговой линии [4]. Оказалось, что с уменьшением масштаба измерения l
длина береговой линии возрастает. Это связано с тем, что при уменьшении масштаба измерения более тонкая структура линии побережья разрешается, поэтому длина береговой линии возрастает. Расходимость длины при уменьшении масштаба измерения связана с неправильным представлением о данной кривой как одномерном обьекте. На самом деле, береговая линия имеет более высокую, дробную размерность - промежуточную между размерностями прямой и плоскости. Поясним на следующем примере [5]. Попытаемся описать двумерную область однопараметрической линией. Линия заполнит область, образуя что-то вроде решетки. Расстояние между полосами будет порядка l
, а число квадратов l
-2. Сумма длин отрезков ломаной равна l
-1 и при уменьшении масштаба измерения расходится. Дело в том, что область двумерна и надо подсчитывать не длину, а площадь, т.е. суммировать квадраты длин. В случае извилистых кривых типа береговой линии, соответственно, надо суммировать дробные степени длин.
В настоящее время идеи фрактальной геометрии получили чрезвычайно широкое распространение. Фрактальная структура оказалась присуща многим физическим явлениям. В свою очередь, дробные фрактальные размерности отражают симметрию фрактальных структур относительно масштабных преобразований и в силу своей универсальности могут служить характеристиками изучаемых систем. Согласно сложившейся точке зрения фрактали разделяют на два класса [5]: регулярные и случайные, статистические. Примерами первых могут служить разнообразные паркеты Серпинского. Как отмечалось выше, перколяционные кластеры на пороге протекания относят к статистическим фракталям.
Опишем вкратце способ вычисления фрактальной размерности. Строится последовательность кружков радиуса R, покрывающих кривую, и подсчитывается площадь объединения всех кружков. Площадь перекрытия нескольких кружков учитывается только один раз. Показатель, описывающий убывание площади с уменьшением радиуса и определяет размерность структуры. Для точки получим 0, а в случае гладкой кривой точки или плоскости ,соответственно, имеем 1 или 2. У фрактальной кривой суммарная площадь объединений кружков равна Rd f. Если 1 < df < 2, то фрактальная кривая занимает положение, промежуточное между линией и плоскостью. Согласно Хаусдорфу, размерность такого объекта равна: D= 1- df
Описанный выше способ введения фрактальной размерности или компактизация фрактальных объектов соответствует нашему интуитивному представлению о том, что если фрактальный объект уложить плотным, без пустот, способом, то он займет область меньших размеров, а именно, пространство дробной размерности.
Остановимся на основных предположениях, лежащих в основе понятия фракталей. Когда мы говорим о расходимости длины береговой линии, то ясно, что это некая математическая идеализация. На самом деле, принципиальная возможность измерить длину, например, с точностью до атомных размеров существует. Поэтому понятие монофрактала вводится для описания промежуточной области: характерный размер мал, но все еще много больше микроскопических размеров системы. С другой стороны, можно представить кривую со сложной иерархической структурой, состоящей из участков с разной степенью извилистости. При этом вероятность появления некоторых участков может быть различна. Тогда такую структуру не опишешь одной размерностью, для каждой системы участков потребуются свои размерности. Следовательно, необходимым условием понятия фрактального объекта является предположение о случайности фаз в соответствующих спектральных разложениях. Помимо метрической хаусдорфовой размерности для любого множества точек евклидового пространства можно ввести топологическую размерность множества. Она определяется следующим образом. Топологическая размерность любого конечного счетного множества точек равна нулю; размерность связного множества равна dt + 1, если это множество можно разрезать на две несвязные части исключением d t - мерного множества точек (проведением dt - мерного разреза). С учетом вышесказанного определим фрактали как множества с различными метрической и топологической размерностями. Подробное обсуждение свойств фракталей см.[3-5].
1.2. Проблемы описания диффузии и проводимости на фракталях.
Физика фрактальных объектов интересна и необычна. Наиболее удивительным представляется то, что многие физические законы, будучи применены к фрактальным объектам, теряют свою универсальность: одни и те же явления в евклидовом пространстве и на фрактальных объектах носят совершенно различный характер. В качестве примера укажем изменение характера диффузии при случайном блуждании по фракталям. Это явление получило название аномальной диффузии. Аномальность заключается в необычной зависимости среднеквадратичного смещения от времени:
X 2 (t) ~ t 2 / (2 + q
) (1)
Отклонение от линейной зависимости по времени удивительно, поскольку эта зависимость считалась универсальной. Поэтому закон (1) многократно проверялся путем численного моделирования. Степенная зависимость (1) для систем вблизи порога по связности является следствием масштабной инвариантности перколяционных систем. Отметим также, что в отличие от диффузии в евклидовом пространстве случайное блуждание на фракталях оказывается чувствительным к мерности пространства. В плоскости все протекательные пути сильно продублированы, в то время как в трехмерном пространстве пути, в основном, имеют одножильный характер. Изменение характера диффузии обусловлено сложной геометрией протекательных путей. В него дают вклад и извилистость путей, и наличие тупиков. Первые работы по моделированию диффузии на перколяционных кластерах были выполнены в 80-х годах [6-8]. Расчеты проводились на решетках размера 50х50 и временем блуждания 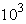 . Были получены оценки для критического индекса аномальной диффузии. Наиболее полное численное моделирование аномальной диффузии для дву- и трехмерного случаев вблизи порога протекания было выполнено в исследованиях [9-11]. Вычисления проводились на векторном компьютере. Моделирование случайного блуждания не представляет значительных трудностей, однако необходимость выполнения большого числа усреднений из-за неоднородности среды требует значительного времени.
. Были получены оценки для критического индекса аномальной диффузии. Наиболее полное численное моделирование аномальной диффузии для дву- и трехмерного случаев вблизи порога протекания было выполнено в исследованиях [9-11]. Вычисления проводились на векторном компьютере. Моделирование случайного блуждания не представляет значительных трудностей, однако необходимость выполнения большого числа усреднений из-за неоднородности среды требует значительного времени.
При попытке строго описать аномальную диффузию сразу возникает вопрос о виде диффузионного уравнения. Помимо собственно уравнения диффузии значительный интерес представляет явный вид функции распределения вероятности в задаче с аномальной диффузией. Ранее предлагались автомодельные выражения, основанные на различных предположениях [12]. Ниже найдено точное выражение для функции Грина в двух моделях.
Другой интересной проблемой является связь между диффузией и проводимостью при аномальном характере случайного блуждания. Впервые этот вопрос рассматривался Эйнштейном для обычной диффузии, было получено известное соотношение:
m
= qD / kT (2)
Здесь m
- подвижность частицы, D - коэффициент диффузии, q - заряд электрона, T - температура, k - постоянная Больцмана. Эти же рассуждения можно повторить и для перколяционных кластеров выше порога протекания. Как известно, проводимости выше порога протекания приписывается свой критический индекс
s
(x) ~ ( x- x c ) t (3)
Поскольку в проводимости могут участвовать только носители, попавшие на бесконечный кластер (БК), постольку проводимость должна быть пропорциональна плотности БК. Но, как показали многочисленные исследования, большая часть БК не проводит, поэтому для описания сложной геометрической структуры протекательных путей было введено представление об эффективном коэффициенте диффузии:
D (x) = s
(x) / P (x) ~ (x-x c )q
(4)
Критический индекс коэффициента диффузии связан с индексами проводимости и плотности соотношением:
t - b
= q
n
(5)
Аналогичная связь между критическими индексами была получена при случайном блуждании на фракталях [13,14]. В этих работах заранее предполагается справедливость линейного отклика. Это так при обычной диффузии, но совсем неочевидно в общем случае. Ниже будет показано, что при аномальной диффузии возможно и иное существенно нелинейное поведение.
Введение электрического поля в задачу о диффузии в неоднородной среде сильно усложняет проблему и это связано с двоякой ролью поля. С одной стороны, оно индуцирует дрейф в направлении поля. С другой, электрическое поле порождает ловушки. Ими являются тупики и участки на токонесущих путях, направленные против поля. Согласно работам [15,16] конкуренция указанных эффектов может привести к немотонной зависимости скорости от поля.
1.3. Интегродифференцирование дробного порядка.
Изложенные выше представления дают только качественную картину диффузионных процессов в сильно неоднородных средах и на фракталях. Для количественного описания случайных блужданий на фракталях необходимо использовать математический аппарат обобщенных производных и интегралов дробного порядка. Отметим, что с математической точки зрения он является достаточно разработанным, однако в теоретической физике производные и интегралы дробного порядка пока не получили широкого применения. На наш взгляд это связано с тем, что до последнего времени не было насущной необходимости в их использовании и в отсутствии ясной физической интерпретации производных дробного порядка. Напомним, что в случае целых производных первая производная соответствует скорости изменения функции, а вторая производная - ускорению.
В настоящей статье на микроскопических моделях будет показано каким образом возникают дробные производные по времени и пространству в обобщенных диффузионных уравнениях, каким физическим ситуациям это соответствует и проанализированы некоторые следствия, вытекающие из обобщенных диффузионных уравнений.
Для дальнейшего удобства мы введем понятия “дифференцирование и интегрирование дробного порядка” и перечислим некоторые основные их свойства.
Перед введением понятий интегралов и производных дробного порядка напомним известное тождество:
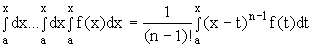 (6)
(6)
(Оно легко доказывается методом математической индукции.) Заметив, что (n -1)!= Г (n) – гамма-функция, нетрудно видеть, что правой части формулы (6) можно придать смысл и при нецелых значениях n. Поэтому естественно определить интеграл дробного порядка 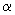 следующим образом:
следующим образом:
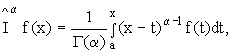 (x >a) (7)
(x >a) (7)
Он называется дробным интегралом Римана-Лиувилля. Путем прямых вычислений легко проверить, что имеет место тождество:
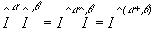 (8)
(8)
Аналогично можно ввести и производные дробного порядка Римана-Лиувилля:
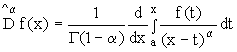 (9)
(9)
Здесь также имеет место тождество:
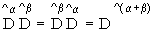 (10)
(10)
Заметим, что порядок действия операторов оказывается существенным:
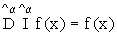 (11)
(11)
но
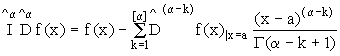 (12)
(12)
Таким образом, операция интегродифференцирования дробного порядка образует некоммутативную группу.
Наиболее просто операции дробного интегродифференцирования выполняются в обратном Лапласовском ( Фурье) пространств, где они просто сводятся к умножению или делению функции на соответствующую дробную степень параметра преобразования:
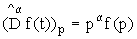 ,
, 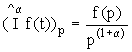 (13)
(13)
2.Микроскопические модели с аномальной диффузией.
2.1. Регулярные фрактали.
Отличительными особенностями регулярных фрактальных структур являются их масштабная инвариантность (подобие самим себе на любых масштабах) и неполное заполнение евклидового пространства. Поэтому фрактальные объекты рассматривают как множества, занимающие промежуточное место между точкой и линиями, линиями и поверхностями, поверхностями и объемами. Наглядным образом фракталей могут служить пористые губки.
В качестве примера напомним способ вычисления фрактальных размерностей для паркетов Серпинского. Простейший треугольный паркет получается следующим образом. Равносторонний треугольник делится на четыре равных треугольника: центральный треугольник выбрасывается. Аналогичная процедура проделывается с каждым из оставшихся треугольников и так до бесконечности. Как уже говорилось выше, фрактальные объекты описываются хаусдорфовыми размерностями. Зафиксируем масштаб А и вычислим на этом масштабе массу паркета М. Она оказывается меньше из-за неполного заполнения пространства: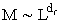 . При изменении масштабов в 2 раза L’=2L будет видна более подробная структура паркета. Нетрудно видеть, что масса М’ возрастает в 3 раза. Следовательно, фрактальная размерность треугольного паркета Серпинского равна:
. При изменении масштабов в 2 раза L’=2L будет видна более подробная структура паркета. Нетрудно видеть, что масса М’ возрастает в 3 раза. Следовательно, фрактальная размерность треугольного паркета Серпинского равна: 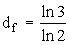 . Аналогичные вычисления дают для прямоугольных паркетов Серпинского:
. Аналогичные вычисления дают для прямоугольных паркетов Серпинского:  и для кривой Коха:
и для кривой Коха: 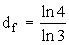 .
.
Рассмотрим случайное блуждание на регулярных фрактальных множествах. Вначале выведем известное уравнение для обычной диффузии с использованием масштабных преобразований. Рассмотрим одномерное случайное блуждание. Зафиксируем некоторый масштаб А с соответствующим временем прыжка t
. Совершим преобразование Лапласа по времени и перейдем в S - представление. Пространственные производные в уравнении диффузии представим в конечно- разностном виде:
( st
) r
( s,x) = D [(r
(s,x +a) - r
(s,x) ) - (r
(s,x ) - r
(s,x-a) )]/ a 2 (14)
где r
(s,x) - плотность диффундирующих частиц. Дальнейший шаг состоит в переходе от масштаба A к масштабу 2A. Это можно сделать, выражая из уравнений вида (1.1) функции r
(s, Х i ) через функции r
(s,x i), где i=1,2,3. Здесь координаты X i соответствуют масштабу 2А.
( st
) r
( s, x2) = D [(r
(s, x1) - r
(s, x 2) ) - (r
(s,x 2) - r
(s,x3) )]/ a 2 (15)
( st
) r
( s, x1) = D [(r
(s,X1) - r
(s, x1) ) - (r
(s, x1) - r
(s, X2) )]/ a 2
( st
) r
( s, x3) = D [(r
(s,X2) - r
(s, x3) ) - (r
(s, x3 ) - r
(s.X3) )]/ a 2
Окончательно, получим перенормированное уравнение диффузии на прямой:
(( st
)2 + st
) r
( s, x) = D [(r
(s,x +2a) - r
(s.x) ) - (r
(s,x ) - r
(s.x-2a) )]/ a 2 (16)
В приближении st
<
<
1, что соответствует большим временам, оно сводится к уравнению (14) простым переобозначением: t
’ = 4t
, a’= 2a. Таким образом, показано, что увеличение масштабов в 2 раза приводит к возрастанию времени прыжка в 4 раза. Далее перейдем от уравнения в конечных разностях к дифференциальному. При фиксированных Х и t устремим параметры а и t
к нулю. Предельный переход конечно не должен зависеть от единиц измерения величин Х и t .Из этого условия устанавливается связь между параметрами а и t
, а именно, способ предельного перехода:
lim (a ) a
/ t
= 2 a
/ 4 * lim (a ) a
/ t
(17)
a ®
0 , t
®
0 a ®
0 , t
®
0
Из (17) следует a
= 2 , как и должно быть. Уравнение диффузии имеет обычный вид. Выполним масштабные преобразования в реальном пространстве для случайного блуждания по кривой Коха. Из рассуждений, аналогичных выше сделанным, получим изменение времени прыжка t
в 16 раз при изменении масштабов в 3 раза. Таким образом, время прыжка имеет порядок A( 2+ q
) . Критический индекс q
аномальной диффузии для кривой Коха равен:
2+ q
= 2 ln (4 ) / ln (3 ) (18)
Следовательно, уравнение диффузии в форме конечных разностей имеет вид:
( st
) r
( s,x) = D [(r
(s,x +a) - r
(s.x) ) - (r
(s,x ) - r
(s.x-a) )]/ a 2+ q
Здесь размерная постоянная D имеет смысл коэффициента диффузии, а выражение в скобках есть нечто иное, как разностная производная по координате Х. Воспользовавшись определением гельдеровской производной дробного порядка
¶
a
F /¶
х a
= lim F( x + d
x) – F(x) / (d
x ) a
x ®
0
получим выражение для диффузионного тока при аномальной диффузии
J (x) = - D ¶
1+q
r
/¶
х 1+q
(19)
Окончательно, получим диффузионное уравнение на фракталях:
¶
r
/ ¶
t = D ¶
2+q
r
/¶
х 2+q
(20)
Оно имеет вид уравнения в дробных пространственных производных.
Таким образом, с помощью масштабных преобразований установлен аномальный характер диффузии на фрактальной кривой и получено обобщенное диффузионное уравнение. Вычислен критический индекс аномальной диффузии. В силу одномерности он также легко устанавливается с помощью следующих соображений. Время диффузионного смещения вдоль одномерной кривой пропорционально квадрату длины, в свою очередь, длина кривой z
связана с расстоянием между концами соотношением:  ~(L)Df. Предполагая степенную связь между временем диффузии TL и расстоянием L, на которое смещается частица, найдем индекс аномальной диффузии:
~(L)Df. Предполагая степенную связь между временем диффузии TL и расстоянием L, на которое смещается частица, найдем индекс аномальной диффузии:
2 + q
= ¶
ln TL / ¶
ln L = 2 D f = 2 ln (4 ) / ln (3 ) (21)
Отметим также, что ренорм-групповой анализ случайного блуждания на фракталях не позволяет однозначно представить уравнение диффузии в виде (20). Возможно также другое альтернативное описание аномальной диффузии. В этом случае уравнение диффузии будет иметь вид уравнения непрерывности с заменой первой производной по времени на производную по времени дробного порядка.
¶
n
r
/ ¶
n
t = D ¶
2 r
/¶
х 2 (22)
Подробно обобщенные уравнения такого типа будут обсуждаться ниже.
Итак, с помощью ренорм-группового анализа установлена необходимость использования аппарата обобщенных производных дробного порядка и предложены возможные обобщенные уравнения, описывающие аномальную диффузию. Использование дробных производных обусловлено как геометрическими свойствами фрактальных структур, так и необычной физикой процессов переноса на фракталях.
2.2. Канторовы множества (КМ).
Аналогично регулярным фракталям строятся канторовы множества. Они занимают промежуточное место между точкой и прямой. Вначале выбирается отрезок длины L. На следующей стадии средняя часть отрезка удаляется и на его концах остаются два отрезка меньшей длины 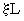 (
(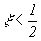 ). На последующем этапе каждый отрезок длины
). На последующем этапе каждый отрезок длины 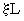 подвергается той же самой процедуре. Длина отрезков после первого этапа деления равна
подвергается той же самой процедуре. Длина отрезков после первого этапа деления равна 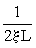 . На втором этапе длина отрезков определяется выр.
. На втором этапе длина отрезков определяется выр. 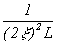 . На n этапе получим длину отрезков:
. На n этапе получим длину отрезков: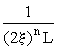 . Следовательно, фрактальная размерность КМ равна:
. Следовательно, фрактальная размерность КМ равна: 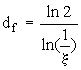 .
.
Интересная физическая интерпретация КМ была предложена в работе [17]. Рассмотрим эволюцию физической системы в течении времени t, где ток в системе J(t) связан с функцией f(t) с помощью функций памяти K(t):
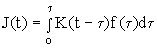 (23)
(23)
Пусть K(t) равна ступенчатой функции:
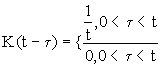 (24)
(24)
Множитель 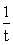 выбирается, чтобы отнормировать функцию памяти на единицу:
выбирается, чтобы отнормировать функцию памяти на единицу:
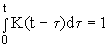 (25)
(25)
Тогда в процессе эволюции система проходит через все состояния непрерывным образом без каких-либо потерь. Вычислим лапласовский образ J(t):
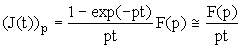 (26)
(26)
Здесь F(p)- лапласовский образ функции f(t), p – параметр преобразования Лапласа. Нетрудно видеть, что формула (26) соответствует полной памяти.
Рассмотрим другой предельный случай, когда в системе имеется только одно состояние с бесконечно большой плотностью: 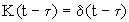 . В этом случае получим:
. В этом случае получим:
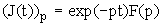 (27)
(27)
Оно соответствует хорошо известному марковскому процессу с полным отсутствием памяти, когда все последующие состояния связываются с предыдущими только через одно текущее состояние в каждый момент.
Эти два предельных случая хорошо известны в физике. Первый соответствует чисто кинетическому обратимому подходу без потерь, а второй случай – диффузионным необратимым процессам. В связи с этим возникает вопрос об эволюции, с асимптотикой промежуточной между описанными выше случаями. Пусть в процессе эволюции часть состояний в системе необратимо теряется, т.е. становится недоступной для системы. Оказывается, такую эволюцию можно описать с помощью множества Кантора. Канторово множество как и регулярные фрактали устроено таким образом, что оно автоматически учитывает недоступность части состояний системы.
3.3. Случайное блуждание по гребешковой модели перколяционных кластеров.
Недавно для изучения аномальной диффузии на перколяционных кластерах была предложена микроскопическая модель гребешковой структуры: проводящая ось, к которой перпендикулярно прикреплены уходящие на бесконечность ребра [18].Эта структура является простейшей моделью скелета бесконечного кластера (совокупности проводник путей, уходящих на бесконечность), которая явно учитывает наличие тупиков ("мертвых концов") на протекательных путях в перколяционных системах.
Особенность диффузии в изучаемой модели состоит в том, что смещение в Х - направлении возможно только вдоль оси структуры. Иначе говоря, коэффициент диффузия D xx отличен от нуля только при у = 0: D xx = D 1 d
(y) (J x = - D xx ¶
n /¶
x ) [19]. Диффузия вдоль ребер носит обычный характер : D yy = D2 .Таким образом, случайное блуждание по гребешковой структуре описывается коэффициентом диффузии в тензорном виде:
|
|
( |
D 1 d
(y) 0 |
0 |
) |
|
|
D |
= |
|
(28) |
| |
|
0 |
D2 |
|
Уравнение диффузии на структуре, соответственно, имеет вид:
( ¶
/ ¶
t - D 1 d
(y) ¶
2 /¶
х 2 - D 2 ¶
2 /¶
y 2 ) r
(x, y, t ) = 0 (29)
Bыполним преобразование Лапласа по времени и преобразование Фурье по координате Х и прейдем в смешанное (s, k, y) -представление.
( ¶
/ ¶
t - D 1 d
(y) k 2 - D 2 ¶
2 /¶
y 2 ) r
(s, k , y ) = 0 (30)
Будем искать функцию Грина уравнения (30) в виде:
G ( s, k , y ) = g (s, k) exp ( - l
½
y½
) (31)
Подставляя решение (31) в уравнение (30), получим уравнения для определения параметра l
:
( s + D2l
2 ) G ( s, k, y)= 0 (32)
Обинтегрировав скачок производной по окрестности У == 0, определим функцию g (s,k):
g (s,k) = ( 2 l
D2 + D 1 k 2 ) – 1 (33)
Окончательно, имеем выражение для функции Грина:
G (s, k, y) = exp ( - (s D2 )1/2 )/ ( 2 l
D2 + D 1 k 2 ) (34)
Следовательно, функция Грина в (x,y, t ) – представлении равна:
¥
G (x, y, t) = ò
exp [ -x 2 /4D1t
- (s D2 )1/2 ( t
+ ÷
y÷
) + st] ¶
t
¶
s/(p
t
D1) 1/ 2 (35)
0
Преобразуем интеграл по параметру S к стандартному путем дифференцирования по параметру t
:
¥
G (x, y, t) = ò
exp ( -x 2 /4D1t
)/ (t
)1/2 ( -¶
/¶
t
exp ( - (s D2 )1/2 ( t
+ ÷
y÷
) + st] ¶
t
¶
s*
0 * (s p
D1) -1/ 2 (36)
Как отмечалось выше, интерес представляет случайное блуждание вдоль оси структуры; именно, оно оказывается аномальным. Соответствующая функция Грина, имеет вид:
¥
G (x, 0, t) = ò
(t
D 2) 1/2 exp ( -x 2 /4D1t
- D2 t
2 /4 t ) ¶
t
/(s p
D1)1/ 2 (37)
0
Асимптотическое выражение функции Грина, на больших временах устанавливается методом перевала:
G (x,0, t) ~ exp ( - const x 4/3 / t1/3 ) (38)
Изучим статистику случайных блужданий вдоль оси гребешковой структуры. Как нетрудно убедиться путем прямых вычислений функция Грина (G (x,0, t) нормирована не на единицу:
<G (x,0, t)> = ò
G( x ,0, t) ¶
x = ( D 2 /p
t ) 1/2 (39)
В этом нет ничего удивительного, поскольку нормирована полная вероятность обнаружить частицу в любой точке структуры. Выражение (38) описывает только вероятность находиться на оси структуры. Иными словами, согласно (38) мы имеем задачу с не сохраняющимся числом частиц. С учетом этого обстоятельства вычислим среднеквадратичное смещение вдоль оси:
< X 2 (t) > = < X2 G > / < G > = ( p
t / D 2 ) 1/2 (40)
Оно зависит от времени аномальным образом. Критический индекс равен: q
=2. Найдем также вероятность возврата в точку начала блуждания. Рассмотрим интеграл (37) при Х=0.
G (0,0,t) ~ ( D2 D 1 2 t 3 ) (41)
Подчеркнем, что результаты (37),(39) и (40) являются точными. При их вычислении было использовано интегральное представление для фикции Грина (35). Обсудим уравнение на величину G (x,0, t) . Как следует из (33) в (s, k ) - представлении оно имеет вид:
( 2 (s D2) 1/2 + D 1 k 2 ) r
(s, k ) = 0 (42)
Используя определение обобщенной производной дробного порядка по времени [15] , получим обобщенное равнение диффузии для плотности частиц на оси структуры:
( ¶
1/2 /¶
t 1/2 + D 1 k 2 ) r
(s, k ) = 0 (43)
где оператор дробного дифференцирования по времени равен:
( ¶
1/2 f /¶
t 1/2 = ò
¶
f /¶
t
¶
t
/ (t - t
) ½
Интегро-дифференциальный вид уравнения диффузии (43) отражает необычный характер случайных блужданий вдоль оси гребешковой структуры. Именно, в каждой точке на оси возможны случайное исчезновение и последующее рождение диффундирующей частицы (уход с оси и возвращение на неЈ).
3. Дрейф и проводимость неоднородных сред и на фракталях.
3.1. Дрейф в модели гребешковой структуры.
Включение электрического поля приводит к анизотропии случайных блужданий. В слабых полях параметр анизотропии мал: a
( E ) << I и пропорционален полю. Соответственно, полевой ток имеет вид: J = n m
E. В гребешковой структуре тензор подвижности аналогично коэффициенту диффузии (28) равен:
| |
|
( |
m
1 d
(y) |
0 |
) |
|
m
|
= |
|
| |
|
0 |
m
2 |
(44)
Уравнение диффузии в электрическом поле по гребешковой структуре имеет вид:
[ ¶
/ ¶
t - d
(y)( D1 ¶
2 /¶
х 2 + m
1 Ex ¶
/¶
х ) - D 2 ¶
2 /¶
y 2
- m
2Ey¶
/¶
y ] r
(x, y, t ) = 0 (45)
Соответственно, в смешанном представлении получим:
[ ¶
/ ¶
t - d
(y)( D1 k 2 + i k m
1 Ex ) - D 2 ¶
2 /¶
y 2
- m
2 Ey ¶
/¶
y ] r
(x, y, t ) = 0 (46)
Пусть поле направлено только вдоль оси структуры: E = E 0 ( 1,0 ,0 ).
Соответственно, функция Грина в смешанном (s ,k, y) – представлении равна:
G (s, k, y) = exp ( - (s D2 )1/2 ½
y½
) / ( 2 l
D2 + D 1 k 2 + i k m
1 Ex ) (47)
Способом подробно обсужденным выше получим выражение для функции Грина, описывающее диффузию и дрейф вдоль оси структуры:
¥
G (x, 0, t; E) = ò
(t
D 2) 1/2 exp ( -x 2 /4D1t
- D2 t
2 /4t ) ¶
t
/(t3p
D1)1/ 2 (48)
0
Найдем первый момент функции Грина в поле:
< X(t)> = m
1 Ex (p
t / D 2)1/2 (49)
Подчеркнем, что отклик на постоянное электрическое поле, оказывается зависящим от времени. Именно, скорость уменьшается со временем по закону:
< V> = m
1 Ex (p
/ t D 2)1/2 (50)
Из (50) также следует, что в задаче аномальной диффузии с дрейфом нельзя подобрать такую сопутствующую инерциальную систему отсчета, которая бы двигалась с постоянной скоростью и в которой бы осталась бы только диффузия. Рассмотрим также влияние электрического поля на вероятность возврата в начало блуждания. В обычной диффузии дрейфовый снос приводит к экспоненциальному уменьшению вероятности возврата в начало блуждания:
G (о, t , E ) = ехр (-(m
E ) 2 t /D ) (51)
В нашем случае как следует из (1.106) на больших временах получим только степенное уменьшение:
G (о, t , E ) ~ t E 3 / 4 / t 3 / 2 (52)
Результат (52) легко понять. Электрическое поле действует на частицы только тогда, когда они попадают на ось структуры. Большую же часть времени частицы проводят на ребрах, вне оси структуры, поэтому и получается более слабая - степенная зависимость.
3.2. Нелинейная подвижность при диффузии по самоподобным кластерам.
Классическая диффузия, когда диффундирующая частица блуждает только по ближайшим соседям достаточно хорошо изучена и разработаны различные методы исследований. Менее известными и исследованными являются случайные блуждания, когда броуновские частицы диффундируют не только по ближайшим соседям. К такому классу диффузионных задач относятся случайные блуждания посредством прыжков Леви. Особенностью прыжков Леви является возможность частицы на каждом шагу смещаться на сколь угодно большие расстояния, так что среднеквадратичное смещение за единичный промежуток времени оказывается бесконечным [20]. Численное моделирование диффузии посредством прыжков Леви показало, что посещенные во время диффузии точки объединяются в кластеры, хорошо разделенные в пространстве. При более подробном рассмотрении оказывается, что каждый из кластеров, в свою очередь, состоит из совокупности кластеров. Таким образом, образуется иерархическая структура из самоподобных кластеров [2]. Следовательно, диффузия Леви представляет случайное блуждание по самоподобным кластерам. Функция распределения вероятности в Фурье- представлении имеет вид:
P( k, t)=exp (-A ï
kï
m
t) (53)
где А и m
- положительные величины, 1<m
<2. Такие распределения называются распределениями Леви. Более подробно о полетах Леви см. также [21].
Ниже будет получено обобщение на случай прыжков Леви и показано, что при диффузии Леви дрейфовая скорость частицы оказывается нелинейной функцией электрического поля, именно:
V ~ Е (m
- 1) (54)
Подчеркнем, что эта нелинейность имеет место в сколь угодно слабых полях и является следствием необычного характера диффузии. Степень нелинейности описывается критическим индексом 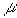 прыжков Леви. Иными словами, закон Ома (линейный отклик на поле) является следствием обычного характера диффузии, при ином характере диффузии – при прыжках Леви закона Ома нет вообще. Наиболее наглядно это видно, когда наряду с прыжками Леви частица может также диффундировать обычным способом. Тогда в соответствие с двумя предельными законами для случайного блуждания скорость частицы также имеет два асимптотических режима: линейный и нелинейный.
прыжков Леви. Иными словами, закон Ома (линейный отклик на поле) является следствием обычного характера диффузии, при ином характере диффузии – при прыжках Леви закона Ома нет вообще. Наиболее наглядно это видно, когда наряду с прыжками Леви частица может также диффундировать обычным способом. Тогда в соответствие с двумя предельными законами для случайного блуждания скорость частицы также имеет два асимптотических режима: линейный и нелинейный.
Рассмотрим одномерный дискретный аналог прыжков Леви [20]. Обозначим вероятность частицы оказаться на l - узле после n шагов Pn(l) и распределение вероятности прыжков по длинам f (l).
¥
P n+1 (l) = å
f (l- m) P n (m) (55)
m = - ¥
В качестве функции f (l) выберем следующую функцию:
¥
f ( l )= å
a - n ( d
l , - b n + d
l , b n ) (56)
n=0
где d
n , m - символ Кронекера.Тогда структурная функция для такого случайного блуждания равна:
¥
l
= ò
f ( l ) exp ( i k l ) d l = å
a - n cos ( k bn ) (57)
n=0
Заметим также, что структурная функция l
удовлетворяет функциональному уравнению
l
(к) = a l
( kb ) + cos (k) (58)
Следовательно, при к ®
0
она должна вести степенным образом с показателем m
= ln a /ln b .Неаналитическое поведение вида ô
kô
m
при к ®
0
с показателем m
можно получить посредством преобразования Меллина, или с помощью формулы суммирования рядов Пуассона. Подробнее см [20,22].
Введем анизотропию в случайное блуждание по самоподобным кластерам. В силу специфики прыжков Леви частица за один шаг может смещаться на любое расстояние bn, поэтому малая анизотропия (1+a
) с a
= qEs /kT при смещении на малое расстояние s оказывается экспоненциально большой на больших расстояниях bn. Поскольку на каждом шагу диффундирующая частица покидает узел, постольку сумма вероятностей движения по W+ и против поля W_ должна равняться единице: W+ + W_ = 1. Отсюда получим выражения для вероятностей движения по и против поля:
bn bn bn
W ±
= ( 1 ±
a
) / [ (1 + a
) + ( 1- a
) ] (59)
Следовательно, структурная функция l
(k; E) при диффузии посредством прыжков Леви в электрическом поле равна:
¥
2 l
( k; E )=å
a- n[cos (kbn) + i sin (kbn ) ( W+ - W_ )] (60)
n=0
Как и при обычной диффузии второе слагаемое при малых k ®
0 содержит дрейфовую скорость:
¥
V = i ¶
l
( k ; E ) / ¶
t ï
k®
0 = å
( b /a ) n * (61)
n=0
bn bn bn bn
{ [(1+a
) -- ( 1- a
) ] / [( 1+ a
) + ( 1- a
) ] } @
¥
»
å
( b /a ) n th (a
bn )
n=0
где th (у) - гиперболический тангенс. Легко также видеть, что дрейфовая скорость удовлетворяет функциональному уравнению:
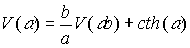 (62)
(62)
Следовательно, в сколь угодно слабых полях скорость должна зависеть от электрического поля степенным образом с показателем 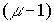 .Для точного вычисления воспользуемся формулой Пуассона:
.Для точного вычисления воспользуемся формулой Пуассона:
¥
¥
¥
å
f ( n )= 1/2 f(0) + ò
f(t) d t + 2 å
f (t) cos ( 2p
mt )
n=0 0 m =1
В нашем случае f (t ) = (b/a) t th (a
bt ). Сделав две замены t' = t ln b и z = exp t', получим для функции f(z) = z - m
th (a
z ). Следовательно,
¥
¥
- g
m
V (a
) = a
/2 + a
(m
-1) [ å
ò
th (z) z dz + (63)
m = -¥
1
a
- g
m
+ ò
th(z) z dz ]
0
где показатель равен g
m = m
+ 2p
mi /ln b
Нетрудно видеть, что второе слагаемое в скобках мало по сравнению с первым по параметру a
. Таким образом, в сколь угодно слабых электрических полях получаем для скорости нелинейную по электрическому полю зависимость (54). Отметим также, что как неаналитическое поведение структурной функции при k ®
0, так и нелинейная зависимость скорости от электрического поля в сколь угодно слабых полях являются асимптотическими. Недавнее численное моделирование показало справедливость развитых теоретических представлений [23].
4. Заключение.
В настоящей работе на примере микроскопических моделей регулярных фракталей, канторовых множествах, гребешковой модели перколяционных кластеров и самоподобных иерархических кластерах рассмотрены диффузионные процессы на этих объектах. Установлено, что они носят необычный аномальный характер: как субдиффузионный, так и супердиффузионный. Выведены обобщенные диффузионные уравнения. Они существенно отличаются от обычных диффузионных уравнений гиперболического вида. Именно, как было описано выше в зависимости от постановки задачи вместо обычных производных целого порядка возникают производные дробного порядка. Таким образом, показано, что для описания аномальных случайных блужданий на фракталях и самоподобных объектах необходимо использовать математический аппарат интегродиференцирования дробного порядка. Описаны физические ситуации, когда возникают дробные производные по времени или по пространству в обобщенных уравнениях диффузии и дана интерпретация полученных результатов. Наиболее существенным представляется вывод о возможности отсутствия линейного омического отклика фрактальных систем в сколь угодно слабых полях.
Рассмотренные выше модели не учитывают полностью сложной геометрии перколяционных кластеров. Заранее ответить на вопрос: какая из моделей и насколько адекватно описывает дрейф частицы на перколяционных кластерах нельзя. Поэтому нами было проведено численное моделирование дрейфа (и диффузии) на перколяционных кластерах. Опишем кратко алгоритм моделирования. С помощью датчика случайных чисел генерировалась квадратная решетка размером 400 и 500 постоянных решетки с заданной долей выбитых узлов вблизи порога протекания. Это хорошо известная задача узлов теории протекания. Далее моделировалось случайное блуждание по такой случайной решетке с периодическими граничными условиями. Точка начала блуждания выбиралась произвольно. Вероятность пойти по одному из четырех направлений определялась выпадением случайного числа в интервале [0, 1], разбитом на четыре равных части. Если на выбранном направлении узел оказывался выбитым, то опять следовал случайный выбор направления до тех пор, пока не совершался переход на ближайший узел. Число неудачных попыток не учитывалось в общем числе шагов. Конфигурации, в которых начало блуждания приходилось на пустой узел или не было ближайших целых узлов не учитывались при подсчете среднеквадратичного смещения. Усреднение проводилось по случайно выбранным точкам начала диффузии и по реализациям случайной перколяционной решетки. Общее число усреднений было порядка 250. Анизотропия прыжка (электрическое поле) моделировалось неравномерным разбиением интервала [0 ,l]. Именно, длина отрезка, соответствующая движению по полю (против поля) увеличивалась (уменьшалась) на величину анизотропии a
(E). Программа проверялась на однородной среде и гребешковой структуре. Результаты моделирования собственно диффузии на кластерах совпадают с известными [6-8]. Мы увидели следующую картину. На малых временах подвижность частицы уменьшается со временем степенным образом:
m
( t) ~ m
0 / t g
(64)
Показатель g
численно приблизительно равен 1/3. Уменьшение подвижности со временем является следствием ухода частиц с токонесущих путей в мертвые концы и извилистости протекательных путей. Кроме того, найдено стационарное значение подвижности на больших временах (10 5 шагов) и в сильных электрических полях qEL c /kT >> 1. Подвижность оказалась сильно нелинейной функцией электрического поля. ЕЈ можно экстраполировать экспоненциальной зависимостью:
m
(E) ~ m
0 exp ( - qEL c /kT) (65)
Сильное уменьшение подвижности обусловлено экспоненциально малой вероятностью прохождения участков токонесущих путей, направленных против поля. Действительно, вероятность сделать против поля N шагов пропорциональна:
W ~ ( 1 – qEa /kT ) N ~ exp ( - qEaN/kT ) (66)
Суммарная длина таких участков порядка корреляционного радиуса Lc, так что
N ~ L c / a .
Настоящая работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 99-02-17355)
Литература
- Broadbent S.R., Hammersley J.H., Proc.Cаmbr.Phil.Soc.1957.V.53.P.6292. Mandelbrot B., Fractals: Form,Chance and Dimension.San -Francisco Freeman.1977
- Stauffer D., Introduction to percolation theory.Taylor & Francis.London.1985
- Соколов И.М., УФН.1986.Т.150.С.221
- Зельдович Я.Б., Соколов Д.Д., УФН.1985.Т.143.С.493
- Pandey R., Stauffer D., Phys.Rev.Lett.1983.V.51.P.527
- O'Shaugnessy, I.Procaccia, Phys.Rev. A.1985.V.32.P.3073
- Zabolitzky J.C., Phys.Rev.B.1984.V.30.P.4077
- Hong D.,Havlin S. et al., Phys.Rev.B.1984.V.30.P.4083
- Sahimi M., J.Phys.A.1984.V.17.L379
- Шкловский Б.И., Эфрос А.Л., Электронные свойства легированных полупроводников- М.: Наука.1979
- G.Weiss., S.Havlin, Physica A.1986.V.134.P.474
- S.R. White, M. Barma, J.Phys. A 17, 2995 (1984)
- Gefen Y.,Aharony A.,Alexander S., Phys.Rev.Lett.1983. V.50.p.77
- Alexander S.,Orbach R., J.de Phys.Lett.1982.V.43.P.L625
- Sarychev A.,Vinogradoff A., J.Phys.C.1979.V.12.с.681
- Rammal R.,Angles d'Auriac J.,Benoit A., J.Phys.A. 1984.V.17P.L491
- Архинчеев В.Е.,Баскин Э.М., ЖЭТФ.1990.Т.100.С.293
- Джрбашян М.М., Интегральные преобразования и представления функций в комплексной плоскости.М.:Наука.1966 г.
- B.D. Hughes, M.F. Shlesinger, E.W.Montroll, Proc.Natl.Acad.Sci (USA)78, 3287 (1981)
- G. Zumofen, J. Klafter., Physica D. V.69.P.436, Phys.Rev.E.V.47.P.851 (1993)
- В.Е. Архинчеев, Письма в ЖЭТФ. 67, 518 (1998), ЖЭТФ, 115, 561 (1999)
- В.Е. Архинчеев, А.В. Номоев, Physica A, V.269 (1999) in press

