ГОЛОГРАММА С ЗАПИСЬЮ НА НЕЛИНЕЙНОСТИ ВТОРОГО ПОРЯДКА
Ю.Н. Денисюк, А. Андреони*, М.А.С. Потенца*.
Физико-технический институт им. А.Ф. Иоффе РАН, г. Санкт-Петербург, Россия
* - Университет г. Комо, Италия
Рассмотрен
новый метод кросс-корреляции волновых фронтов посредством
так называемой генерирующей вторую гармонику голограммы (ГВГ
голограмма). В соответствии с этим методом в нелинейном светочувствительном
материале, характеризующемся нелинейностью второго порядка,
записывается картина интерференции объектной и референтной
волн. Полученная таким способом голограмма генерирует волну
с удвоенной частотой колебаний, которая формирует реконструированное
изображение без какой-либо задержки в момент времени, когда
интерферирующие волновые фронты пересекают светочувствительный
материал. Получено выражение, определяющее электрическое поле
восстановленной голограммой волны. На основе этого выражения
разработан графический метод построения волнового фронта,
реконструированного голограммой. Показано, что поперечные
размеры восстановленного ГВГ голограммой изображения равны
поперечным размерам регистрируемого объекта, а продольные
размеры увеличены в два раза. Показано, что изменения положения
референтного источника также приводят к изменениям положения
и масштаба восстановленного изображения. Предложено использовать
свойства ГВГ голограммы для создания системы переключающихся
межсвязей, которые действуют по принципу “свет управляет светом”.
Предложена и рассмотрена схема элемента такой системы. Проведен
эксперимент по записи ГВГ голограммы. Голограмма записывалась
в кристалле ВВО с помощью неодимового (Nd:Yag) лазера. Эксперимент
подтвердил способность ГВГ голограммы формировать изображение
с высоким разрешением. Эксперимент подтвердил также справедливость
полученных закономерностей изменения масштаба и положения
восстановленного изображения в зависимости от изменения длины
волны генерируемого излучения, а также положения референтного
источника.
Введение.
Голографический метод записи и реконструкции волновых
полей, предложенный более 50 лет тому назад, широко используется
в настоящее время в науке и технике [1-3]. Одним из важных
направлений развития применений этого метода являются голографические
запоминающие устройства, переключаемые межсвязи и другие элементы
компьютерной техники и техники оптической связи [4-7]. На
ранних стадиях развития этой области голограммы записывались
на обычных фотопластинках, однако с 70-х годов для этой цели
стали использоваться так называемые динамические голограммы,
которые записываются в нелинейных светочувствительных средах,
способных изменять свой показатель преломления под действием
падающего на них излучения. Постоянная времени реакции таких
материалов, как правило, очень мала и поэтому динамические
голограммы допускают запись и считывание информации в реальном
масштабе времени.
В
последнее время был предложен новый метод трансформации волновых
фронтов, позволяющий осуществлять такие трансформации вообще
без какой-либо временной задержки посредством так называемой
кросс-корреляции излучения второй гармоники [10]. Этот метод
основан на использовании нелинейности второго порядка нелинейных
светочувствительных материалов. Восстановленное волновое поле
формируется в этом случае излучением, длина волны которого
вдвое меньше длины волны излучения, взаимодействующего с нелинейной
средой.
Как
будет показано далее, хотя запись такого рода не позволяет
запомнить информацию даже на очень короткое время, она позволяет
осуществлять трансформации волновых полей, подобные тем, которые
выполняются обычной голограммой, в связи с чем такую запись
естественно назвать “генерирующая вторую гармонику голограмма”
(ГВГ голограмма). Трансформации, осуществляемые ГВГ голограммой
могут быть использованы для кодирования и декодирования сигналов,
для переключения межсвязей компьютеров и стекловолоконных
линий связи, а также осуществления других аналогичных операций.
В
своих первоначальных публикациях авторы данного метода использовали
теоретический подход, характерный для нелинейной оптики [10,11].
Такой подход очень удобен при описании процесса взаимодействия
света с нелинейной средой, однако он встречается с рядом трудностей,
когда необходимо описать трансформации пространственной конфигурации
волновых полей, восстановленных голограммой. При рассмотрении
таких трансформаций значительно удобнее использовать методы
анализа, принятые в голографии. В частности в данном случае
необходимо доказать саму возможность формирования изображений
произвольных объектов с помощью ГВГ голограммы, а также определить
масштаб и положение этих изображений в пространстве.
2.Структура
изображения, сформированного ГВГ голограммой
Оптическая
схема записи ГВГ голограммы идентична схеме записи внеосевой
голограммы (Рис.1). Картина интерференции волны Eo,
рассеянной объектом O и сферической референтной волны
ER , испущенной точечным источником R,
записывается в нелинейном материале H, способным к
нелинейности второго порядка, в частности в описанных ранее
экспериментах в качестве нелинейной светочувствительной среды
использовался b - кристалл бората бария (ВВО1) [10].
При
последующем анализе процессов в ГВГ голограмме мы будем исходить
из того, что толщина нелинейной среды пренебрежимо мала, хотя
реально голограммы такого типа записываются в толстослойных
нелинейных средах с целью лучше использовать слабые эффекты
нелинейности. Анализ, который приводится ниже, можно рассматривать
как исследование процессов, протекающих в одном из сечений
реального кристалла (сечение S на рис.1.). Следует
отметить, что при использовании одноосевого двупреломляющего
кристалла (ВВО), оптическая ось лежит в плоскости Рис.1. Значения
электрических полей объектной волны Eo и
референтной волны ER в плоскости S голограммы
H можно записать следующим образом:
Eo
= Ao (r ) exp {i[k1 Lo (r
) + w t ]}, (1)
ER
= AR exp {i[k1LR (r
) + w t ]}, (2)
где Ao
- амплитуда сложной объектной волны, зависящая от координаты
“r”; Lo (r ) и LR (r
) - эйконалы объектной и референтной волн, которые описывают
форму их волновых фронтов. Эйконалы представляют собою функции
распределения оптических путей лучей от объекта O и
референтного источника R до плоскости S. Значение
суммарного электрического поля Ew в плоскости
S будет равно сумме Eo и ER:
Ew
= Ao (r ) exp {i[k1 Lo (r
) + w t ]} + AR exp {i[k1LR
(r ) + w t ]}. (3)
|
|
|
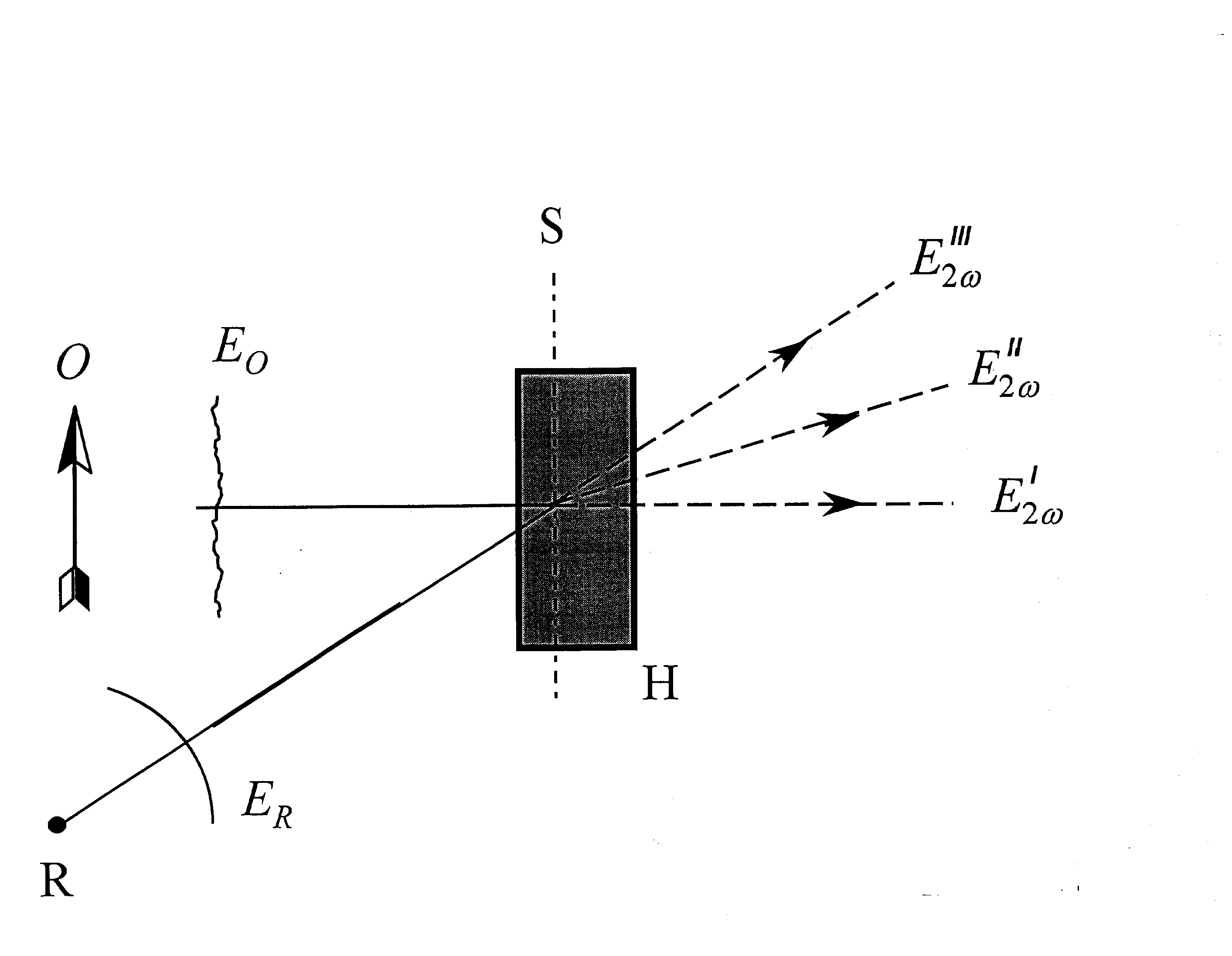
Рис.1.
Оптическая схема записи ГВГ голограммы. O - объект;
H - голограмма; Eo и
ER
— объектная и референтная волны с частотой w
, записываемые на голограмме; E¢
2w
, E²
2w ,
E¢ ²
2w —
волны второй гармоники с частотой 2w
, генерируемые голограммой; при этом E²
2w
является
реконструированной волной; S — произвольное плоское
сечение голограммы.
|
Нелинейный
материал H освещенной волной Ew генерирует
вторичную волну с частотой 2w . В соответствии с законами
нелинейной оптики волна, генерируемая средой с восприимчивостью
c (2) определяется следующим выражением
[12]:
E2w
= m Ew Ew ,
(4)
где “m”
- некоторая постоянная, Ew - первичное электрическое
поле, взаимодействующее со средой, E2w -
вторичное волновое поле, генерируемое нелинейным материалом.
Значение электрического поля E2w ,
генерируемого ГВГ голограммой, может быть найдено посредством
подстановки значения Ew из выражения (3) в выражение
(4).
E2w
µ A2o (r ) exp {i[2k1
Lo (r ) + 2w t ]} + 2Ao (r
) AR exp {i[k1 Lo (r ) +
LR (r ) +
2w
t ]} + A2R exp {i[2k1LR
(r ) + 2w t ]} ( 5)
Из выражения
(5) прежде всего следует, что частота колебаний электрического
поля, восстановленного ГВГ голограммой, в два раза больше,
чем частота электрического поля записываемого на ней излучения.
Значение волнового вектора 
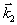 соответственно увеличивается также вдвое
соответственно увеличивается также вдвое
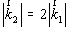 (6)
(6)
где  - значение волнового вектора электрического поля, восстановленного
ГВГ голограммой;
- значение волнового вектора электрического поля, восстановленного
ГВГ голограммой; 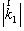 -
значение волнового вектора электрического поля, записанного
на ГВГ голограмме. Подставляя уравнение (6) в уравнение (5),
получим окончательное выражение для электрического поля E2w
излучения, восстановленного ГВГ голограммой
-
значение волнового вектора электрического поля, записанного
на ГВГ голограмме. Подставляя уравнение (6) в уравнение (5),
получим окончательное выражение для электрического поля E2w
излучения, восстановленного ГВГ голограммой
E2w
µ A2o (r ) exp {i[k2
Lo (r ) + 2w t ]} +
2Ao (r ) AR exp 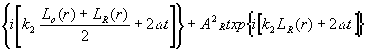
 (7)
(7)
Из уравнения
(7) следует, что в отличие от обычной голограммы, которая
восстанавливает волновое поле, состоящее из четырех компонент,
волновое поле, восстановленной ГВГ голограммой, состоит из
трех компонент (E¢ 2w ; E²
2w ; E¢ ² 2w
на рис.1.) Так называемая сопряженная волна в этом случае
отсутствует. Рассмотрим структуру волн, восстановленных ГВГ
голограммой, более подробно.
Как
и в случае обычной голограммы, изображению, восстановленному
ГВГ голограммой, соответствует компонента волнового поля,
возникающая в результате интерференции объектной и референтной
волн. В выражении (7) этой компоненты соответствует второй
член. При дальнейшем анализе удобно рассматривать роли эйконала
Lo (r ) объектной волны и эйконала LR
(r ) референтной волны в отдельности. В связи с
этим запишем второй член E² 2w
уравнения (7) в следующем виде:
E²
2w
= Ao (r ) exp [ik2 Lo
(r )/2 ] + AR exp [ik2LR (r
)/2 ] x exp(i2w t). (8)
Процесс
формирования изображения определяется первым множителем уравнения
(8), роль второго множителя будет рассмотрена позднее. Восстановленное
ГВГ голограммой изображение может быть найдено с помощью ряда
последовательных трансформаций исходного изображения объекта
O1 (см. рис.2а и 2в). На рис.2а представлен
объект O1, который рассеивает излучение
с длиной волны l 1 . Волновое поле
рассеянного объектом излучения характеризуется некоторым распределением
фаз Fo(x1 , y1 , l
1 ) в плоскости S , в которой записывается
голограмма. Соответствующая изображению компонента восстановленного
голограммой излучения характеризуется распределением фаз FH
(x1 , y1 , l 2
). Поскольку 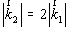 (см. выражение (6), то ik2Lo(r )/2=
ik1Lo(r), т.е. показатель экспоненты
выражен (8), описывающий фазу восстановленной волны, совпадет
с показателем экспоненты выражения (1), описывающем фазу волны
излучения, рассеянного объектом. Учитывая это обстоятельство,
можно записать
(см. выражение (6), то ik2Lo(r )/2=
ik1Lo(r), т.е. показатель экспоненты
выражен (8), описывающий фазу восстановленной волны, совпадет
с показателем экспоненты выражения (1), описывающем фазу волны
излучения, рассеянного объектом. Учитывая это обстоятельство,
можно записать
FH
(x1 , y1 , l 2
) = Fo(x1 , y1 , l
1
) (9)
Таким
образом, оказывается, что распределение фаз излучения, восстановленного
голограммой, совпадает с распределением фаз излучения, рассеянного
объектом, однако длина волны восстановленного излучения в
два раза меньше длины волны излучения, рассеянного объектом.
Задача состоит в том, чтобы определить изображение, соответствующее
распределению фаз FH (x1 , y1
, l 2 ). Исходный объект O1
определен в системе координат (x1 , y1
, z1) и находится на расстоянии z1¢
от плоскости голограммы S. Его поперечные
размеры характеризуются отрезком l1 . В
качестве исходного пункта рассуждений рассмотрим очевидный
случай, когда все размеры объекта, а также длина волны освещающего
его излучения уменьшены в два раза (см. рис.2в). Примем также,
что в 2 раза уменьшен также и масштаб системы координат (x2
, y2 , z2), в которой измеряются
параметры волнового поля, рассеянного объектом излучения.
Очевидным и существенным для рассмотрения является тот факт,
что
|
|
|
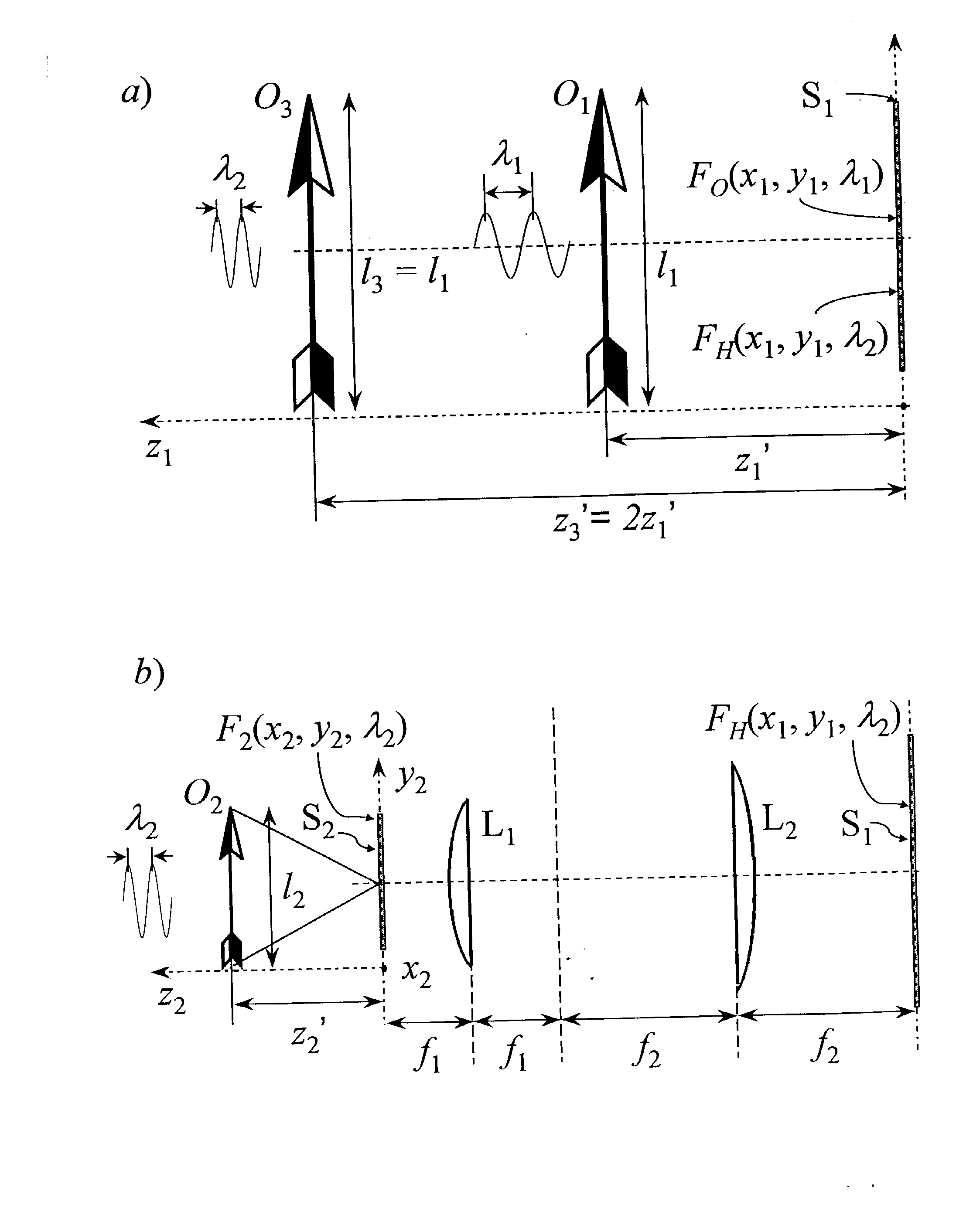
Рис
2а), в) Схемы вертуальных трансформаций первоначального
изображения O1
, используемые при определении конфигурации восстановленного
изображения.
2а)
O1
— объект, освещенный излучением с длиной волны l
1 и
определенный в системе координат x1
, y1 , z1 ;
O3 —
изображение, восстановленное голограммой в излучении
с частотой 2w .
2в)
O2 —
уменьшенный в два раза исходный объект, освещаемый
излучением с частотой 2w
; L1
и
L2
— линзы телескопической системы с двукратным увеличением
проецирующей объект O2
.
|
функция
распределения фаз F2(x2 ,
y2 , z2) излучения, рассеянного
масштабированным объектом O2 совпадает в
масштабированной системе координат с функцией распределения
фаз Fo(x1 , y1 , l
1 ) излучения, рассеянного исходным объектом
O1 , поскольку оптические пути излучения
и длина волны изменяются в одно и то же количество раз:
F2
(x2 , y2 , l 2
) = Fo(x1 , y1
, l 1
). (10)
Дальнейшая
задача заключается в том, чтобы привести распределение фаз
F2 (x2 , y2 , l
2 ) , которому заведомо соответствует определенное
изображение, к распределению фаз FH (x1
, y1 , l 2 ) восстановленного
голограммой излучения и попытаться найти таким образом изображение,
которое соответствует этому распределению. Операцию увеличения
в два раза масштаба системы координат, в которых задано распределение
фаз F2 (x2 , y2
, l 2 ), может осуществлена с помощью
телескопической оптической системы с двукратным увеличением.
Система такого рода, состоящая из линз L1 и
L2 , у которой ¦ 2 =
2¦ 1 , показана на рис. 2в. В соответствии
с общими свойствами телескопических систем поперечное увеличение
этой системы равно 2, а продольное — равно 4.
Передняя
фокальная плоскость линзы L1 помещается
в плоскость S2, где задано это распределение
F2 (x2 , y2 , l
2 ). В соответствии со свойствами телескопической
системы в задней фокальной плоскости S1
линзы L2 формируется распределение фаз,
совпадающее с распределением фаз в плоскости S2,
однако заданное в масштабированной в 2 раза системе координат
(x1 , y1 ,). Как это следует
из приведенного ранее сопоставления функций распределения
фаз Fo(x1 , y1
, l 1 ), F2 (x2
, y2 , l 2 ) и FH
(x1 , y1 , l 2
) (см. выражения (9) и (10). Распределение фаз в выходной
плоскости S1 телескопической системы совпадает
с распределением фаз излучения, восстановленного голограммой
и характеризуется той же длиной волны l 2
. Вместе с тем, в случае телескопической системы не представляет
труда определить конфигурацию изображения, созданного волновым
полем, сформированным в ее задней плоскости S1.
На самом
деле, изображая плоскость S2 в плоскость
S1, телескопическая система в то же самое
время проецирует также и масштабированный объект O2
, создавая его изображение O3 . (Для наглядности
сравнения с исходным объектом O1 изображение
O3 перенесено на рис.2а.). В соответствии
со свойствами телескопической системы поперечные размеры изображения
O3 в два раза превышают поперечные размеры
изображения масштабированного в два раза объекта O2
, т.е. поперечные размеры восстановленного ГВГ голограммой
изображения совпадут с поперечными размерами исходного объекта
O1. Так как продольное увеличение телескопической
системы равно 4, а расстояние от масштабированного объекта
O2 до плоскости S2
вдвое меньше расстояния от исходного объекта O1
до плоскости голограммы S1 , то
в конечном итоге восстановленное голограммой изображение O3
будет удалено от ее плоскости на расстояние Z¢ 3
вдвое большее соответствующего расстояния Z1¢
исходного объекта O1 ( см.рис.2а).
Таким
образом полученный результат можно сформулировать следующим
образом: ГВГ голограмма восстанавливает изображение, поперечные
размеры которого равны поперечным размерам регистрируемого
объекта, а все продольные размеры увеличены в два раза.
3.
Пространственная корреляция волновых полей с помощью ГВГ голограмма
Как это
следует из уравнений (7) и (8) амплитуда и фаза волны, реконструированной
ГВГ голограммы, зависят от соответствующих параметров как
объектной, так и референтной волн. В частности эйконалы Lo(x,y)
, LR (x,y) и LH (x,y)
объектной, референтной и реконструированной голограммой волн
связаны следующим выражением:
LH
(x,y) = 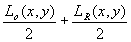 (11)
(11)
Формально
фазы объектной и референтной волн равноправны по отношению
к их влиянию на фазу волны, восстановленной ГВГ голограммой,
однако фактически референтная волна влияет только на положение
и отчасти на масштаб восстановленного изображения. На структуру
восстановленного изображения референтная волна не влияет,
поскольку, являясь либо сферической, либо плоской, она не
имеет собственной структуры.
Рассмотрим
сначала простейший случай взаимного влияния объектной и референтной
волн, когда они представляют собою плоские волны, распространяющиеся
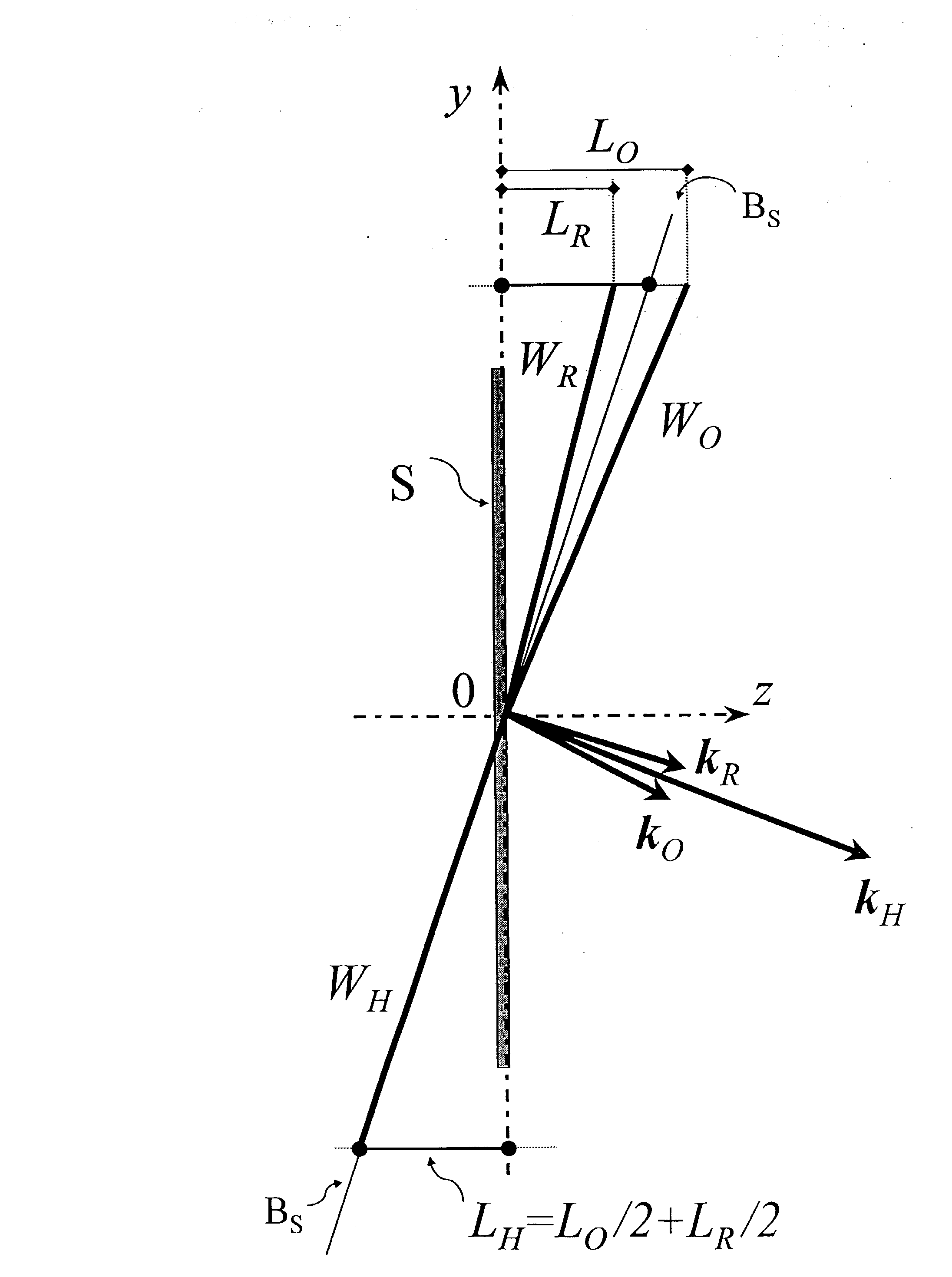
под некоторым углом друг к другу (см.рис.3). Процесс записи
ГВГ голограммы представим в верхней части рис.3 (при y
> 0). Волновые фронты Wo и WR
, характеризующиеся волновыми векторами 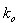 и
и
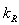 , взаимодействуют
с тонким слоем S нелинейного кристалла. Наклон волновых
фронтов по отношению к плоскости S определяется эйконалами
Lo(y) и LR(y),
которые по существу представляют собою расстояния точек волновых
фронтов от плоскости S в зависимости от координаты
y.
, взаимодействуют
с тонким слоем S нелинейного кристалла. Наклон волновых
фронтов по отношению к плоскости S определяется эйконалами
Lo(y) и LR(y),
которые по существу представляют собою расстояния точек волновых
фронтов от плоскости S в зависимости от координаты
y.
Процесс
построения волнового фронта излучения, восстановленного голограммой,
показан в нижней части рис.3 (y < 0). Складывая
в соответствии с выражением (11) расстояния волновых фронтов
Wo и WR от плоскости S
и деля сумму попалам, найдем отрезки, характеризующие расстояния
волнового фронта WH , восстановленного голограммой
излучения от поверхности голограммы S . Как это видно
из результатов такого построения восстановленная голограммой
волна WH распространяется вдоль бисектриссы
угла, составленного направлениями распространения объектной
и референтной волн. Следует отметить, что этот факт следует
также из теории и эксперимента нелинейной оптики, однако там
он объясняется иным способом [10,11].
|
|
|
Рис.3.
Схема графического построения волнового фронта,
восстановленного голограммой в случае, когда с голограммой
взаимодействуют две плоских волны; S—
тонкий слой нелинейного материала, Wo
—
“объектная” волна; WR
— референтная волна; WH
— волна, реконструированная голограммой.
|
Рассмотрим
более общий случай записи ГВГ голограммы, когда объектная
волна Wo образует изображение произвольного
объекта O1 , а референтная волна WR
является сферической волной. Если этот случай и может быть
как-то рассмотрен с помощью теоретического аппарата нелинейной
оптики, то такое рассмотрение будет во всяком случае очень
сложным. Вместе с тем этот случай записи ГВГ голограммы достаточно
обычен, в частности именно этому случаю соответствовали условия
рассмотренного далее эксперимента.
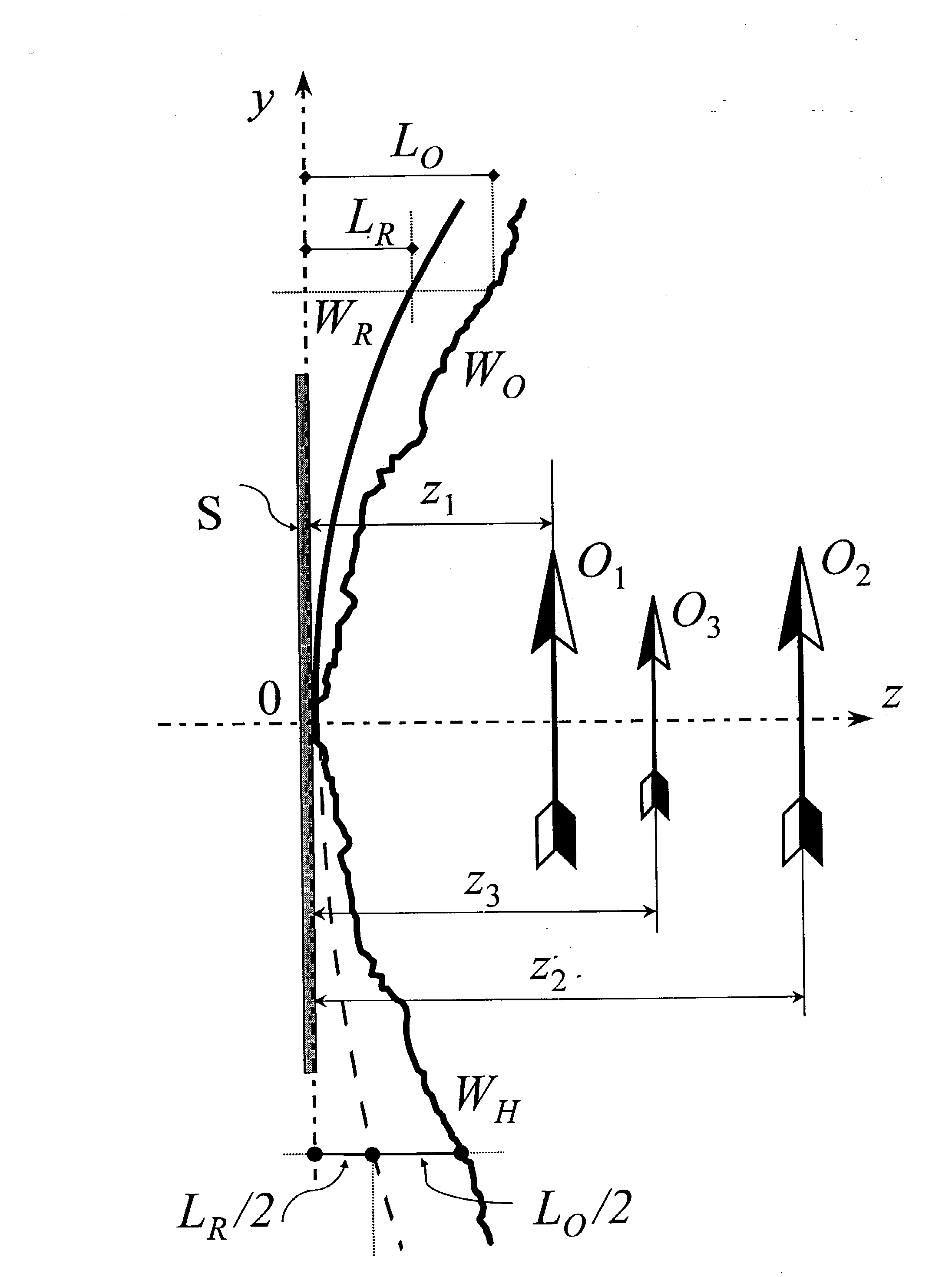
Этап
записи голограммы представлен в верхней части рис.4 (y
> 0). Волновые фронты объектной и референтной волн (Wo
и WR) описываются эконалами Lo(xy)
и LR(xy). Процесс формирования волнового
фронта WH, восстановленного ГВГ голограммой,
показан в нижней части рис.4 (y < 0).
|
|
|
Рис.4.
Схема графического построения волнового фронта восстановленного
голограммой в случае, когда объектная волна Wo
является волной, рассеянной произвольным объектом
O1,
а референтная волна WR
является сферической волной. O2
—
промежуточное изображение; O3
—изображение,
реконструированное голограммой.
|
Этот
процесс может быть представлен в виде последовательности двух
преобразований волновых фронтов. На первом этапе формируется
волновой фронт, которому соответствует эйконал Lo(xy)
/2. Этот волновой фронт образует промежуточное изображение.
В соответствии с проведенным ранее рассмотрением поперечные
размеры этого изображения совпадают с соответствующими размерами
исходного объекта O1 . В продольном направлении
все размеры изображения увеличены в 2 раза, т.е. в данном
случае Z2 = 2Z1 .
На втором этапе волновой фронт, образующий промежуточное изображение
O2 , подвергается дополнительному фазовому
сдвигу LR (xy)/2, вноcимому референтной
волной WR . В результате этого сдвига промежуточное
изображение O2 трансформируется в окончательное
изображение O3 . Закономерности, соответствующие
преобразованию изображения O2 в изображение
O3 , соответствуют преобразованиям, осуществляемым
линзой, фокусное расстояние которой в 2 раза превышает радиус
сферической референтной волны.
Рассмотрим
кратко одно из возможных применений свойства ГВГ голограммы
осуществлять кросс-корреляцию волновых полей.
Как это
следует из уравнения (8), амплитуда реконструированной волны
представляет собою произведение амплитуд объектной и референтной
волн. Из этого следует весьма простой факт, что ГВГ голограмма
генерирует реконструированную водну только в те моменты времени,
когда амплитуда референтной волны отлична от нуля.
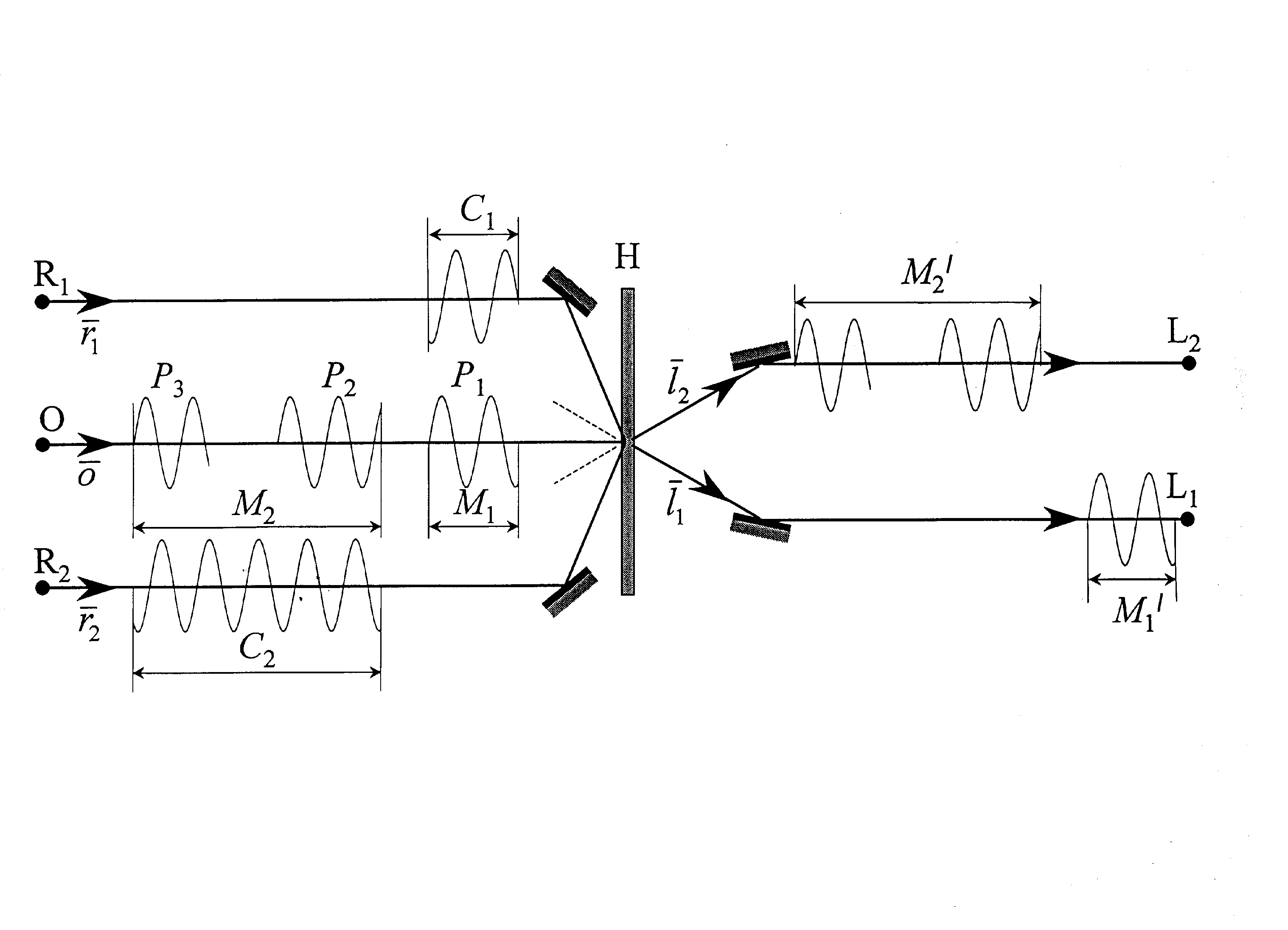
На рисунке
5 представлена схема элемента системы переключаемых линий
межсвязей, основанная на свойствах ГВГ голограммы: Входная
линия O представляет собою лазерный луч о, несущий
сигналы, состоящие из двух сообщений. Первое сообщение M1
представляет собою одиночный импульс P1
. Второе сообщение M2 представлено двумя
импульсами P2 и P3.
|
|
|
Рис.5.
Схема элемента переключаемой системы межсвязей,
основанной на использовании ГВГ голограммы. O
— луч лазера несущей сообщения M1
и
M2 , R1
и
R2
— лучи лазера, несущие приказы о соединении линии
O
, либо с выходной линией L1
, либо с L2
.
|
Программа
распределения сообщений между выходными линиями L1
и L2 передается по входным линиям
R1 и R2 ( лазерные лучи
r1 и r2), которые несут
приказания о подключении или отключении входной линии O
с выходными линиями L1 и L2
соответственно.
Распоряжения,
которые передаются по линиям R1 и R2
представляют собой импульсы света, продолжительность которых
равна интервалу времени, в течение которого передается соответствующее
сообщение. В частности импульс С1 перекрывает
интервал времени, соответствующий продолжительности сообщения
M1 , импульс С2 перекрывает
время сообщения M2 .
Лучи
света 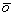 ,
, 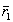 и
и 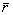 2,
распространяющиеся по входным линиям O, R1 и
R2 пересекают друг друга в объеме ГВГ голограммы
H. В соответствии с присущими ей свойствами ГВГ голограмма
генерирует световой луч l1 , который распространяется
вдоль биссектрисы угла, образованного лучами
2,
распространяющиеся по входным линиям O, R1 и
R2 пересекают друг друга в объеме ГВГ голограммы
H. В соответствии с присущими ей свойствами ГВГ голограмма
генерирует световой луч l1 , который распространяется
вдоль биссектрисы угла, образованного лучами 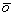 и
и 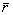 . Этот луч генерируется
только в те моменты времени, когда импульс P1
( сообщение M1) встречается с импульсом
С1 (приказ включить выходную линию L1).
Аналогично импульс С2 , взаимодействуя с
импульсами P2 и P3 (сообщение
M2 ) направляет их в выходную линию L2
. Таким способом сообщения, передаваемые по линии O
, могут быть посланы либо в линию L1, либо
в линию L2 .
. Этот луч генерируется
только в те моменты времени, когда импульс P1
( сообщение M1) встречается с импульсом
С1 (приказ включить выходную линию L1).
Аналогично импульс С2 , взаимодействуя с
импульсами P2 и P3 (сообщение
M2 ) направляет их в выходную линию L2
. Таким способом сообщения, передаваемые по линии O
, могут быть посланы либо в линию L1, либо
в линию L2 .
4. Эксперимент
Способность
ГВГ голограммы восстанавливать изображения объектов была проверена
на эксперименте. В качестве объекта мы использовали точечный
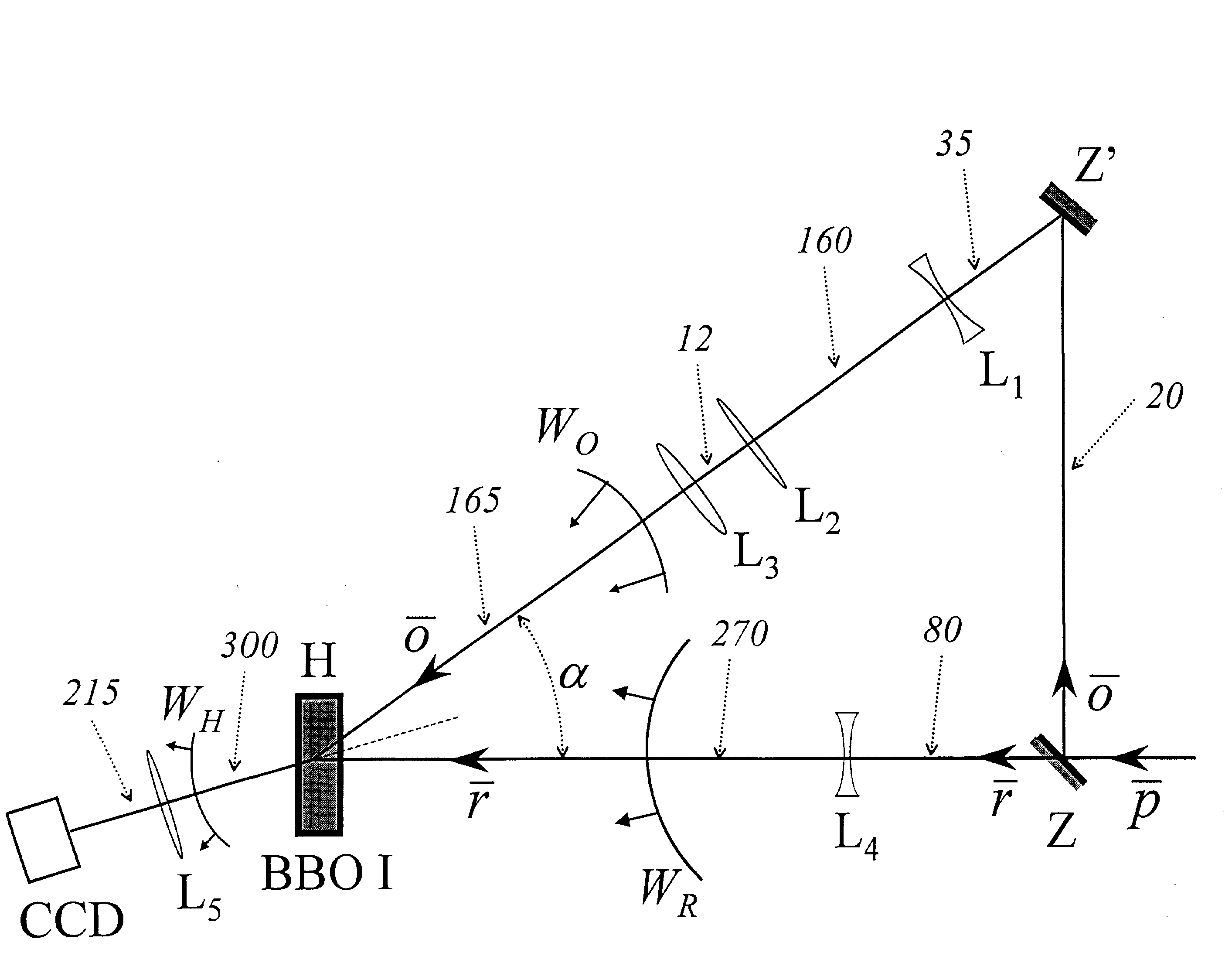
источник света, сформированный линзой. Оптическая схема эксперимента
представлена на рис.6. Импульсный неодимовый лазер (Nd:YAg)
испускает луч света 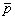 с длиной волны l = 1,06 мкм, который расщепляется полупрозрачным
зеркалом Z на объектный и референтный лучи
с длиной волны l = 1,06 мкм, который расщепляется полупрозрачным
зеркалом Z на объектный и референтный лучи 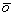 и
и 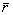 соответственно.
Объектный луч
соответственно.
Объектный луч 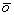 расширяется
с помощью линз L1 и L2
и затем трансформируется линзой L3 в сферическую
волну Wo, которая фокусируется в точку,
играющую роль объекта. Референтный луч
расширяется
с помощью линз L1 и L2
и затем трансформируется линзой L3 в сферическую
волну Wo, которая фокусируется в точку,
играющую роль объекта. Референтный луч 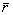 фокусируется линзой L4 в сферическую расходящуюся
волну WR . Объектная и референтная волны
пересекаются в объеме кристалла ВВО, образуя голограмму, которая
формирует расходящуюся сферическую волну WH
. Центр расходимости этой волны представляет собою восстановленное
изображение объекта. Экспериментальная установка характеризовалась
следующими параметрами: Энергия импульсов лазера составляла
около 70 м.дж при длительности импульса 18 н.сек и частоте
повторений 10 гц. Толщина кристалла ВВOI была 0,3 мм при размере
5х5 мм. Кристалл был изготовлен Академимпек Будапешт. Фокальные
расстояния линз L1 L5 оптической
схемы экспериментальной установки были следующими ¦ 1
= – 5 мм, ¦ 2 = + 100 мм, ¦ 3
= + 30 мм, ¦ 4 = – 20 мм, ¦ 5
= + 150 мм. Расстояния между элементами оптической системы
показаны на рис.6.
фокусируется линзой L4 в сферическую расходящуюся
волну WR . Объектная и референтная волны
пересекаются в объеме кристалла ВВО, образуя голограмму, которая
формирует расходящуюся сферическую волну WH
. Центр расходимости этой волны представляет собою восстановленное
изображение объекта. Экспериментальная установка характеризовалась
следующими параметрами: Энергия импульсов лазера составляла
около 70 м.дж при длительности импульса 18 н.сек и частоте
повторений 10 гц. Толщина кристалла ВВOI была 0,3 мм при размере
5х5 мм. Кристалл был изготовлен Академимпек Будапешт. Фокальные
расстояния линз L1 L5 оптической
схемы экспериментальной установки были следующими ¦ 1
= – 5 мм, ¦ 2 = + 100 мм, ¦ 3
= + 30 мм, ¦ 4 = – 20 мм, ¦ 5
= + 150 мм. Расстояния между элементами оптической системы
показаны на рис.6.
|
|
|
Рис.6.
Схема экспериментальной установки для записи ГВГ
голограммы. H —
кристалл ВВО, в котором записывалась голограмма;
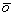 и
и 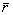 — объектный
и референтный лучи; Wo
—
объектная волна, формирующая точечный объект, записываемый
на голограмме; ССD — ПЗС камера, использовавшаяся
для запис восстановленного изображения; L1
... L5 —
линзы оптической системы с фокусным расстоянием:
¦ 1
= –5мм, ¦ 2
=
+100 мм, ¦ 3
=
+30 мм, ¦ 4
= –20
мм, ¦ 5
=+150
мм.
— объектный
и референтный лучи; Wo
—
объектная волна, формирующая точечный объект, записываемый
на голограмме; ССD — ПЗС камера, использовавшаяся
для запис восстановленного изображения; L1
... L5 —
линзы оптической системы с фокусным расстоянием:
¦ 1
= –5мм, ¦ 2
=
+100 мм, ¦ 3
=
+30 мм, ¦ 4
= –20
мм, ¦ 5
=+150
мм.
|
Измерения
положения, восстановленного голограммой изображения точечного
источника были выполнены с помощью ПЗС камеры. Изображение
фокусировалось в плоскость приемника с помощью линзы L5
(см.рис.6). Измерения показали, что точечное изображение располагается
на линии BS , являющейся биссектрисой угла,
составленного объектным и референтным лучами 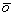 и
и 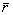 . (см. рис.7).
Расстояние от кристалла до изображения составило d exp
= 205 мм. Изображения точки, восстановленной ГВГ голограммой,
показано в левой части рис.8. На уровне 50% интенсивности
диаметр изображения точки был равен 25 мкм. Прежде чем приступить
к эксперименту, мы оценили фазовое рассогласование волн, генерируемых
ГВГ голограммами в различных сечениях кристалла. Рассогласование
такого рода характерно для неколлинеарных схем генерации второй
гармоники.
. (см. рис.7).
Расстояние от кристалла до изображения составило d exp
= 205 мм. Изображения точки, восстановленной ГВГ голограммой,
показано в левой части рис.8. На уровне 50% интенсивности
диаметр изображения точки был равен 25 мкм. Прежде чем приступить
к эксперименту, мы оценили фазовое рассогласование волн, генерируемых
ГВГ голограммами в различных сечениях кристалла. Рассогласование
такого рода характерно для неколлинеарных схем генерации второй
гармоники.
Фаза
j S волны генерируемой голограммой,
записанной в сечении S , находящемся на глубине X
от поверхности кристалла, определяется следующим соотношением:
j
S
= ç kR+kOç
x = kH x , (12)
где 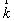 o
и
o
и 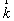 R
- волновые векторы объектной и референтной волн. Учитывая
геометрию записи ГВГ голограммы (см.рис.7), нетрудно определить,
что фаза j S определяется следующим
соотношением:
R
- волновые векторы объектной и референтной волн. Учитывая
геометрию записи ГВГ голограммы (см.рис.7), нетрудно определить,
что фаза j S определяется следующим
соотношением:
j
S = 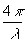 n ( 1 –
n ( 1 – 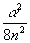 )
x, (13)
)
x, (13)
где l
- длина волны излучения, падающего на кристалл, a - угол
между объектным и референтным лучами на входе в кристалл.
В то же самое время волна второй гармоники, генерируемая
на входе в кристалл, т.е. в сечении x=0, распространяясь
через кристалл, приобретает на глубине x следующую
форму j o :
j
o = 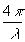 nx . (14)
nx . (14)
Из формул
(13) и (14) следует, что на выходе из кристалла, т.е. при
x = d разность фаз волн, генерируемых на его входе
и выходе составляет:
D
j = j o – j S
= 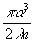 d . (15)
d . (15)
Подставляя
в соотношение (15) параметры эксперимента a =0,075; n=1,6;
d = 0,3 мм, получим D j = 0,5p . Учитывая, что
сумма волн, генерируемых всеми сечениями кристалла обратится
в ноль, т.е. они погасят друг друга, при условии D j
= 2p , можно считать, что фазовый сдвиг D j
= 0,5p достаточно приемлем. В соответствии с законами
трансформации, рассмотренными на рис.2. , восстановленное
голограммой изображение O² должно располагаться
на удвоенном расстоянии d ¢ = 277,6 мм от кристалла
(см. рис. 7).
Однако
это положение восстановленного изображения не является окончательным,
так как необходимо еще учесть дополнительную фокусировку,
вносимую сферической референтной волной, как это было показано
ранее (см.рис.3). Учитывая параметры оптической схемы, нетрудно
подсчитать, что центр расходимости сферической волны, сформированной
линзой L4 , расположен на расстоянии d
R = 290 мм. Фокусирующее действие, которое
такая волна оказывает на восстановленное изображение, эквивалентно
действию отрицательной линзы с фокусным расстоянием 580 мм,
которая расположена во входной плоскости кристалла. Проведя
необходимые вычисления, нетрудно определить, что в соответствии
с теорией восстановленное изображение Oth
должно находиться на расстоянии d th
=188 мм от кристалла. Полученное теоретическое значение находится
в хорошем соответствии со значением d exp
= 205 мм, полученном на эксперименте.
Результаты
эксперимента по определению структуры изображения, восстановленного
ГВГ голограммой показали, что это изображение характеризуется
разрешением, близким к дифракционному. Результаты регистрации
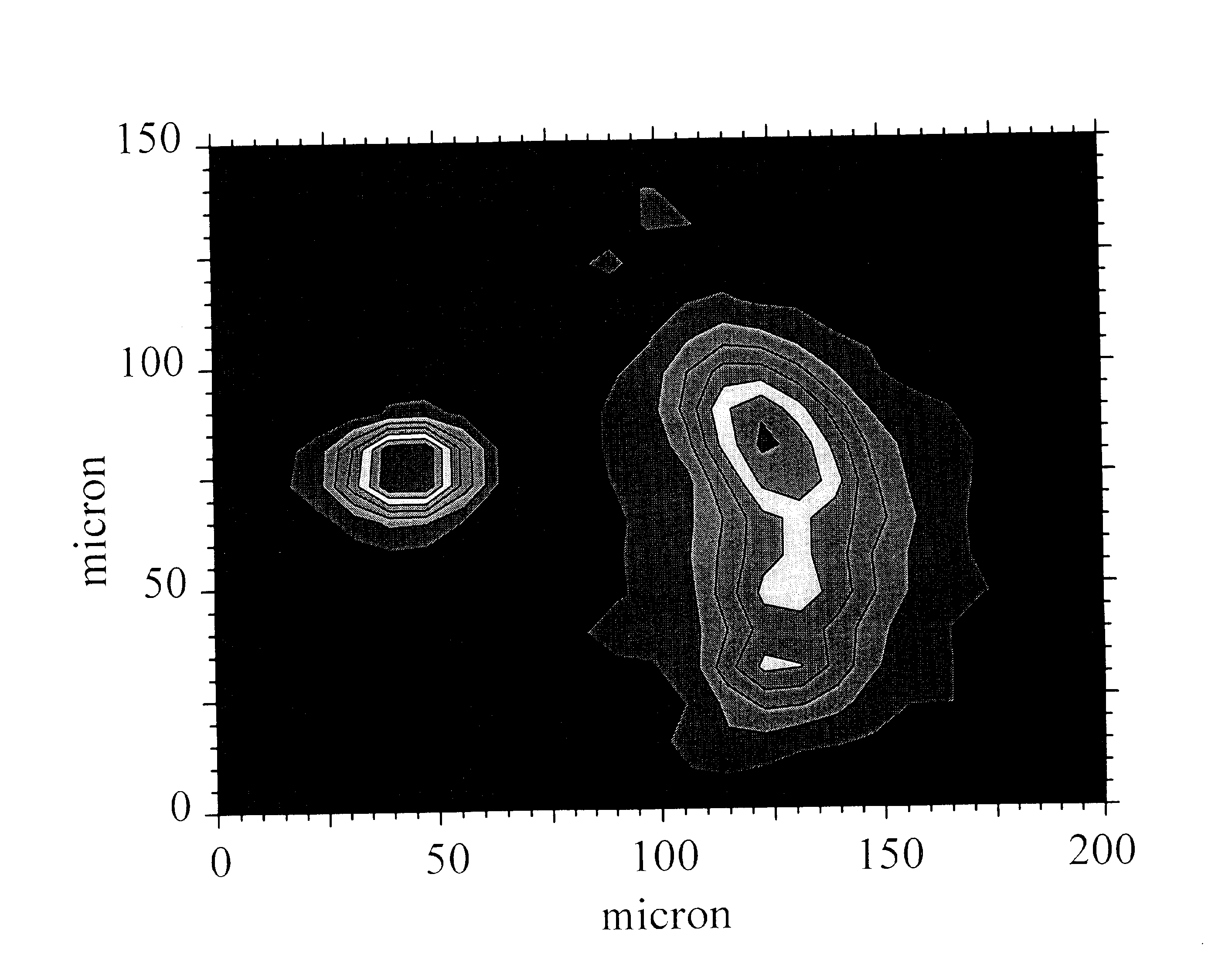
изображения с помощью ПЗС камеры приведены на рис.8. В левой
части рисунка помещена фотография изображения в случае, когда
оно было сфокусировано на приемник ПЗС камеры. На уровне интенсивности,
равном 50%, размер изображения по горизонтали был равен 30
мкм, а по вертикали — 20 мкм. В правой части фотографии приведена
картина, которую можно было наблюдать в случае, когда изображение
было расфокусировано на величину 2,87 мм. Конфигурация светового
пятна в этом случае несимметрична, что по-видимому обусловлено
тем, что в условиях эксперимента левая часть зрачка кристалла
не была заполнена светом.
Экспериментальные
подсчеты показали, что при размере кристалла 5х5 мм и при
длине волны света l = 0,53 мкм, размер изображения точки,
ограниченный условиями дифракции, должен составлять 8,6 мкм,
т.е. в 2,3 раза меньше, чем наблюдаемый на эксперименте. При
этом однако следует учитывать, что предельная разрешающая
способность использованной нами ПЗС камеры составляла 8.2
мкм, т.е. была близка к измеряемой величине. Следует отметить,
что полученное на эксперименте значение разрешения было очень
высоко. В угловой мере оно составляло 1 угловую минуту, т.е.
равно разрешению человеческого глаза.
|
|
|
Рис.8. Изображение реконструированного
изображения, полученное с помощью ПЗС камеры. В
левой части фотографии приведено изображение, наблюдаемое
в случае , когда оно было сфокусировано на приемник.
В правой части приведена картина , наблюдаемая при
расфокусировке камеры на величину 2,87 мм. На уровне
интенсивности 50% размер изображения по горизонтали
был 30 мкм, а по вертикали 20 мкм.
|
5. Заключение
Мы рассмотрели
свойства и возможные области применения так называемой генерирующей
вторую гармонику голограммы (ГВГ голограммы). Голограмма такого
типа записывается в нелинейном светочувствительном материале,
используя нелинейность второго порядка этого материала. В
отличие от обычных голограмм ГВГ голограмма не позволяет хранить
информацию даже в течение очень короткого времени, потому
что она существует только в тот момент, когда формирующие
ее лучи пересекают нелинейный светочувствительный материал.
Вместе с тем, в течение такого короткого промежутка времени
ГВГ голограмма способна осуществить операцию взаимной трансформации
волновых фронтов, которые принимали участие в ее записи, в
частности она способна образовать голографическое изображение
в пространстве. Такое изображение может быть использовано,
например, для проекции матрицы светящихся точек на торцы световодов
стекловолоконных линий связи и других аналогичных целей. Свойство
ГВГ голограммы образовывать изображение, зависящее от пространственно-временных
параметров обоих участвующих в ее записи волновых фронтов,
а также необычно высокая скорость осуществляемых ею преобразований,
позволяют использовать ее для создания переключаемых систем
межсвязей, действующих по принципу “свет управляет светом”.
Такие системы могут найти применение в стекловолоконных линиях
связи, а также при создании вычислительных машин, работающих
на основе использования световых сигналов в качестве единственного
носителя информации.
Авторы
считают своим приятным долгом выразить свою благодарность
С.А. Савич за проведенную ею работу по оформлению статьи с
помощью компьютера. Участие Ю.Н. Денисюка в данной работе
во время его пребывания в г.Комо (Италия) было поддержано
фондом научных исследований КАРИПЛО, а также фондом научных
исследований УниверКомо. Участие М.А.С. Потенца в проведении
исследований по данной теме - фондом Е.Н.Е.А. (для аспирантов).
Литература
- D. Gabor “Microscopy by Reconstructed Wave Fronts” Proc.Roy. Soc. (London). Vol. A 197, pp. 454–(1949)
- E.N.Leith, J.Upatnieks “Wavefront Reconstruction with Diffused Illumination and Three-Dimensional Objects” J.Opt.Soc. Am. Vol.54, pp.1295–1299 (1964).
- Ю.Н.Денисюк “Об отображении оптических свойств объекта в волновом поле рассеянного им излучения”.// Доклады АН СССР. 1962. Т.144. С.1275–1278.
- P.I.Van Heerden “Theory of Optical Information Storage in Solids” Appl. Opt. Vol.2, pp.393–400 (1963).
- H.Sasaki, J.Ma, N.Maunduit, Y.Feinman, S.H. Lee “Digital Holographic Memory for Optoelectronic Neutral Network Modules” Optical Memory & Neural Networks Vol.3, pp. 191–205 (1994).
- A.L. Mikaelian “1–D Holographic Memory for Information Processing”. Proceedings of the SPIE -The International Society for Optical Engineering, Vol.2297, pp.155–163 (1994).
- V.B. Markov, Yu.N.Denisyuk, R.Amezquita “ 3–D Spekle-shift Hologram and its Storage Capacity” Optical Memory & Neural Networs Vol.6, pp.91–98 (1997).
- I.P.Woerdman “Formation of Transient Free Carrier Hologram in Si” Opt. Commun. Vol.2 , p.212– (1970).
- Б.И. Степанов, Е.В. Ивакин, А.С. Рубинов “ О записи плоских и объемных динамических голограмм в отбеливающихся фотоматериалах”. //Доклады АН СССР. 1971. Т.196. С.567.
- A. Andreoni, M. Bondani, M.A.C. Potenza, F. Villani @Phase Selection of Imagedearing Field Components by Frequency Up-conversion in Nonlinear Crystals” J.Nonlin. Opt. Phys.& Mat. Vol.8, p.55-77 (1999).
- A. Andreoni, M. Bondani, M.A.C. Potenza, F. Villani “ Relevance of Temporal Coherence in the Second-harmonic Crocc-correlation Measurement of a Multiply Scattered Laser Pulse” Eur. Phys. J.D. (1999). In press.
B.E. Salech, M.C. Teich “Fundamentals of Photonics”, pp. 739–743 Wiley Series in Pure and Applied Optics, J.W. Goodman Ed.

