КОМПЬЮТЕРНАЯ
ОПТИКА И ЕЕ ПРИЛОЖЕНИЯ
Котляр
В.В.
Институт систем
обработки изображений РАН
443001 Самара,
ул.Молодогвардейская, 151
kotlyar@smr.ru
Введение
У компьютерной
оптики много названий: компьютерная оптика, оптика, синтезированная на компьютере,
бинарная оптика, плоская оптика, дифракционная оптика. Терминология пока не
устоялась, что указывает на интенсивное развитие данной области знаний. Речь
идет о расчете и создании оптических элементов, внешне представляющих собой
пластину с микрорельефом (отражающим или пропускающим). Максимальная глубина
микрорельефа сравнима с длиной волны света ? . Средний период модуляции
(СПМ) микрорельефа может быть от долей ? до сотен и тысяч длин волн. Он
и определяет выбор метода и приближения для решения обратной задачи дифракции
– расчета дифракционного оптического элемента (ДОЭ). Если СПМ микрорельефа ДОЭ
не больше 3? - 5? ,
то требуется использование строгой электромагнитной теории, если СПМ больше
10? - 20? , то применяют
скалярную теорию дифракции Френеля-Кирхгофа, если СПМ больше 100 ? , то
можно использовать приближение геометрической оптики (лучевое приближение).
Приведенные границы достаточно условны и даны для большей конкретики.
Подробнее о компьютерной
оптике можно узнать в монографиях [1-5]. Коллективом автором из ИСОИ РАН подготовлена
и скоро будет опубликована обширная монография по методам компьютерной оптики.
В рамках данной работы будут рассмотрены ДОЭ, которые можно назвать многоканальными
анализаторами, и которые предназначены для разложения световых полей по ортогональным
базисам для различных задач оптической обработки информации. Данные ДОЭ будут
рассчитываться в рамках скалярной теории Френеля.
1 . ДОЭ для разложения
поля по базису Адамара.
В этом разделе рассматривается
базис Адамара, который, как показано в [6], хорошо подходит для анализа отпечатков
пальцев. Преимущества базиса Адамара в его универсальности и простоте оптической
реализации с помощью бинарных фазовых фильтров. Функции Адамара определяются
следующим образом [7]:
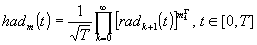 , (1)
, (1)
где 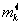 - k-й разряд кода Грея номера m, radm(t)-функции
Радемахера. Код Грея образуется из двоичного номера m по следующему правилу:
- k-й разряд кода Грея номера m, radm(t)-функции
Радемахера. Код Грея образуется из двоичного номера m по следующему правилу:
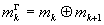 , (2)
, (2)
где k -
номер двоичного разряда (справа налево); mk - двоичный разряд
в двоичной записи номера m:  а знак ? означает сложение по модулю 2. Функции Радемахера определяются
следующим образом:
а знак ? означает сложение по модулю 2. Функции Радемахера определяются
следующим образом:
 (3)
(3)
Двумерные функции
Адамара определяются как произведение одномерных:
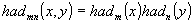 . (4)
. (4)
Базис Адамара обладает
следующими интересными свойствами: 1) функции Адамара удовлетворяют условию
нуля, которое означает, что их Фурье-образы равны нулю в центральной точке;
2) они принимают только два значения: +1 или -1; и 3) определены на ограниченном
интервале. На рис. 1 представлены
примеры некоторых функций Адамара.
(0,0) (0,1) (2,0) (1,2) (2,2) (2,3)
Рис. 1. Примеры
некоторых функций Адамара (белый цвет соответствует значению +1, а черный -
значению -1).
В этом разделе рассмотрен
итеративный метод расчета фазовых ДОЭ, пропускающая функция которых представляет
собой произвольную линейную комбинацию конечного числа функций Адамара с различными
несущими пространственными частотами. Оптическая схема вычисления вектора признаков
изображения w(x,y) показана на рис. 2.

Рис. 2. Оптическая
схема для параллельного вычисления набора коэффициентов разложения светового
поля по ортогональному базису.
Если ДОЭ, имеющий
пропускающую функцию ? в виде линейной комбинации конечного числа базисных
функций  с различными
несущими пространственными частотами:
с различными
несущими пространственными частотами:
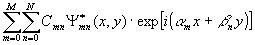 , (5)
, (5)
дополнить сферической
линзой L и осветить волной w(x,y), интенсивность света
в заданных точках фокальной плоскости линзы (um=a
mf/k, vn=b
n f/k) будет пропорциональна
квадрату модуля коэффициентов разложения Cmn этого светового
поля по базису  :
:
 . (6)
. (6)
Пусть необходимо
рассчитать фазу оптического элемента j (x,y), формирующего (при
освещении световым пучком с амплитудой A0(x,y)) коэффициенты
разложения Адамара в заданных точках (a m, b n)
частотной плоскости. Комплексная функция пропускания такого элемента должна
удовлетворять следующему соотношению:
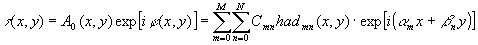 . (7)
. (7)
Если разность между
соседними частотами |a m+1 - a m|
выбрана достаточно большой, т.е. такой, чтобы пространственные спектры соседних
функций Адамара разделялись между собой по некоторому критерию, то коэффициенты
Cmn в ур. (7) приближенно равны
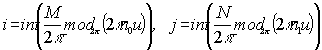 . (8)
. (8)
Заметим, что коэффициенты
Cmn могут быть вычислены с помощью одного преобразования Фурье,
используя уравнение
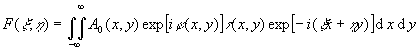 . (9)
. (9)
В этом случае функция
F(x ,h )
в точках плоскости (x ,h ) с координатами (a m,
b n) равна соответствующим коэффициентам
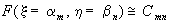 . (10)
. (10)
Предыдущие выкладки
позволяют предложить следующий итеративный алгоритм [8] нахождения фазы оптического
элемента j (x,y). В качестве начальной оценки фазы выбирается j
0(x,y). Предположим, что на k-ой итерации мы
получили k-ю оценку фазы: j k(x,y). Используя
функцию j k(x,y), вычисляются коэффициенты 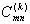 из ур. (8) или ур. (9). Затем они заменяются на коэффициенты
из ур. (8) или ур. (9). Затем они заменяются на коэффициенты
 (11)
(11)
с заданными модулями
Bmn. Далее, коэффициенты 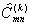 подставляются в (7). В результате суммирования (7) получается функция Ek+1(x,y),
аргумент которой служит последующей оценкой фазы:
подставляются в (7). В результате суммирования (7) получается функция Ek+1(x,y),
аргумент которой служит последующей оценкой фазы:
j
k+1(x,y)
= arg Ek+1(x,y), (12)
и так далее.
Алгоритм использовался
для расчета фазового оптического элемента согласованного с базисом Адамара.
Как видно из рис.3a фаза пропускающей функции такого ДОЭ, учитывая бинарный
характер функции Адамара и согласованность несущей с шагом дискретизации, может
иметь всего 4-5 уровней, что упрощает его изготовление методами микролитографии.
После 10 итераций отклонение квадратов модулей коэффициентов, сформированных
с помощью рассчитанного ДОЭ в частотной плоскости (см. рис. 3б), от идеальных
составило менее 9%.
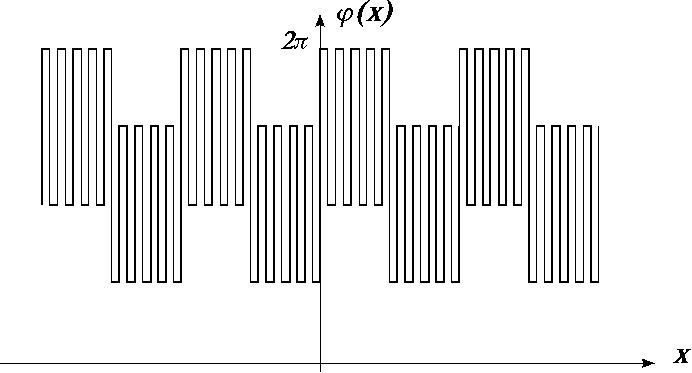
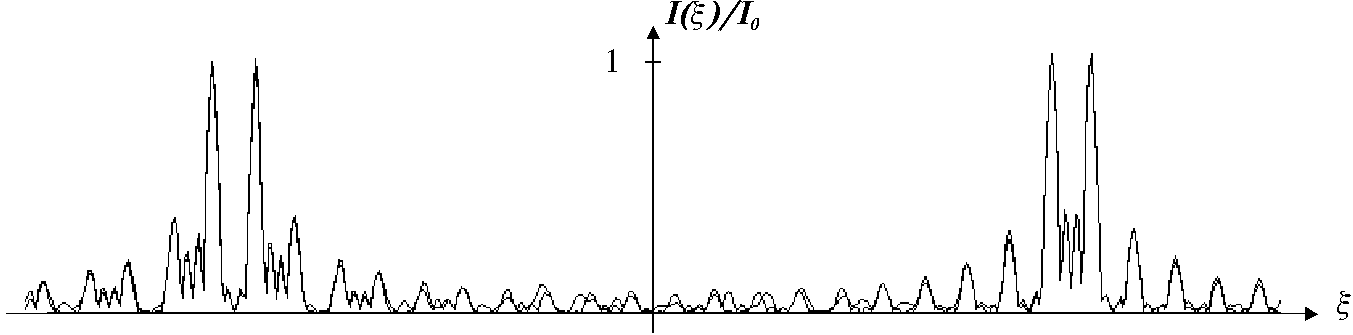
Рис. 3. a) Фаза
оптического элемента, формирующего 3-й и 4-й коэффициенты одномерного разложения
Адамара и б) нормированная интенсивность в плоскости пространственного спектра
(плоскость формирования квадратов модулей коэффициентов).
Также предложенный
алгоритм применялся для расчета ДОЭ, предназначенного вычислять первые 25 коэффициентов
двумерного разложения Адамара 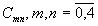 .
В этом случае были выбраны следующие параметры. Общее число пикселов 512´
512. Количество членов суммы N=M=10. Амплитуда освещающего пучка
A0(x,y) была выбрана постоянной.
.
В этом случае были выбраны следующие параметры. Общее число пикселов 512´
512. Количество членов суммы N=M=10. Амплитуда освещающего пучка
A0(x,y) была выбрана постоянной.
На рис. 4a показана
рассчитанная за 5 итераций фаза ДОЭ, который формирует первые 25 коэффициентов
двумерного разложения Адамара в плоскости пространственного спектра. На рисунках
4б и 4в представлены распределения интенсивности в фокальной плоскости
при освещении фазового ДОЭ пучком света с амплитудой A0(x,y)=had00(x,y)
(пик в точке (a 0, b 0) плоскости (x
,h )) и A0(x,y)=had32(x,y)
(пик в точке (a 3, b 2)), соответственно.
Около 80% энергии
падающего света идет на формирование заданных коэффициентов. Среднеквадратичная
ошибка коэффициентов, получаемых с помощью такого ДОЭ не превышает 20% и сравнима
с технологическими ошибками изготовления.
Рассчитанный ДОЭ
может использоваться в задаче анализа изображений. В [6] показано, что коэффициенты
разложения Адамара полей направлений отпечатков пальцев хорошо подходят для
распознавания таких изображений.
Заметим, что без
существенных изменений предложенный алгоритм может быть применен для расчета
ДОЭ, выполняющих оптическое вычисление коэффициентов разложения Уолша и Хаара.
a б в
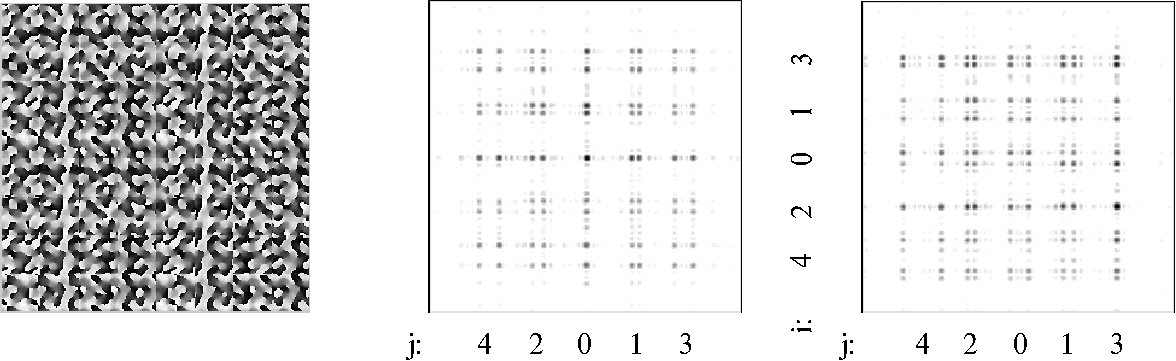
Рис. 4. a) Фаза
ДОЭ, формирующего первые 25 коэффициентов двумерного разложения Адамара, б)
распределение интенсивности в плоскости пространственного спектра при освещении
ДОЭ световым пучком с амплитудой A0(x,y)=had00(x,y) и
в) с амплитудой A0(x,y)=had32(x,y).
2. ДОЭ для разложения
поля по базисам
с угловыми гармониками
В задаче распознавания
изображений инвариантно к их повороту в плоскости наблюдения целесообразно использовать
пространственные фильтры, разделяющие когерентное световое поле на отдельные
дифракционные составляющие специальных ортогональных базисов, содержащих угловые
гармоники. Под угловыми гармониками понимается комплексные функции с единичным
модулем и линейной зависимостью от полярного угла. Такие гармоники появляются,
например, в Бессель-оптике [9] при оптическом выполнении преобразования Ханкеля
высшего порядка, или при генерации бездифракционных пучков [10], бездифракционных
изображений [11], бесселевых пучков с продольной периодичностью [12], многомодовых
вращающихся пучков Гаусса-Лагерра [13].
В этом разделе
рассматривается итеративный алгоритм расчета фазовых ДОЭ, которые могут быть
названы угловыми спектральными анализаторами,
служащими для разложения когерентного светового поля по ортогональному базису
с угловыми гармониками. Сферическая линза фактически играет
роль Фурье-анализатора, так как она раскладывает световое поле на плоские волны
или пространственные Фурье-гармоники. Аналогично, комбинация "линза+ДОЭ" может
быть названа Бессель-, Гаусса-Лагерра-, или Цернике-анализатором если данный
оптический элемент раскладывает лазерный свет по соответствующему базису. Разложение
по модам Гаусса-Лагерра используется при селекции поперечных мод на выходе многомодового
волокна с параболическим профилем показателя преломления. Базис круговых полиномов
Цернике используется при анализе аберраций волновых фронтов.
Комплексная амплитуда
F(x,y) монохроматической световой волны, представленная в полярных координатах
(r,j ) всегда допускает разложение в функциональный ряд Фурье по
угловым гармоникам. Такой функциональный ряд записывается следующим образом
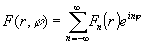 , (13)
, (13)
где 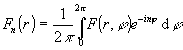 . (14)
. (14)
Ряд (13) дает аналогичное
разложение по гармоникам 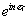 пространственного
спектра данного светового поля. Действительно, если мы возьмем преобразование
Фурье от функции F(r,j
), то получим, что
пространственного
спектра данного светового поля. Действительно, если мы возьмем преобразование
Фурье от функции F(r,j
), то получим, что
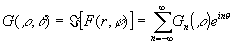 ,
(15)
,
(15)
где  ,
(16)
,
(16)
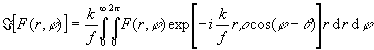 , (17)
, (17)
k - волновое
число, f - фокусное расстояние линзы и
Jn(x) - функция
Бесселя первого рода и n-го
порядка. В ур. (16)-(17) предполагается,
что преобразование Фурье выполняется оптически с помощью сферической линзы с
фокусным расстоянием f
(см. рис.2) .
Разложение в ур-и
(13) удобно использовать при инвариантном к повороту распознавании изображений,
так как поворот анализируемого изображения F(r,j ) на угол ?
j не приведет к изменению экспериментально измеренных модулей коэффициентов
|Fn(r)|. В связи с этим задача инвариантного к повороту распознавания
изображений может быть сведена к измерению коэффициентов разложения изображений
по следующим предлагаемым ниже базисам.
Рассмотрим функции,
описывающие отдельные бездифракционные моды Бесселя, распространяющиеся
в свободном пространстве [11]:
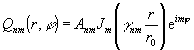 , (18)
, (18)
 , (19)
, (19)
где r0
- радиус апертуры, ограничивающей пучок Бесселя, ? nm
- корни функции Бесселя: Jm(? nm)=0, n,m=
0,1,2, …; and J’m(? nm) - производная от функции
Бесселя в точке r = r0.
Множество функций
в (18) является полным ортогональным базисом внутри круга радиуса r0.
Подставляя их в ур. (13) и (15), можем записать:
 , (20)
, (20)
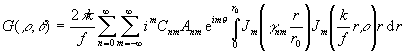 . (21)
. (21)
При 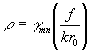 ,
некоторые члены в ур. (21) равны нулю в соответствии со свойством ортогональности
функций Бесселя:
,
некоторые члены в ур. (21) равны нулю в соответствии со свойством ортогональности
функций Бесселя:
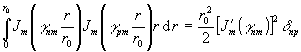 . (22)
. (22)
Базисные функции
в ур. (18) удобно использовать для селекции отдельных бесселевых мод в многомодовом
пучке. Такой многомодовый бесселевый пучок может быть на выходе светового волновода
со ступенчатым профилем показателя преломления.
Моды Гаусса-Лагерра
[13] представляют полное множество ортогональных функций на всей плоскости:
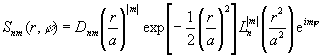 , (23)
, (23)
где 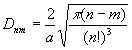 , (24)
, (24)
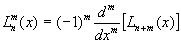 , (25)
, (25)
a - радиус
перетяжки гауссового пучка, 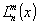 и
и 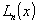 - обобщенные
и обычные полиномы Лагерра, соответственно.
- обобщенные
и обычные полиномы Лагерра, соответственно.
В этом случае,
разложения (18) и (21) по угловым гармоникам будет следующим:
 , (26)
, (26)
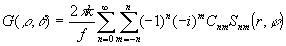 . (27)
. (27)
Уравнение (27) следует
из того, что функции в ур. (23) являются собственными функциями преобразования
Фурье
 . (28)
. (28)
Базисные функции
из ур-и (23) используются при расчете анализатора, согласованного с многомодовым
пучком на выходе из светового волокна с параболическим профилем показателя преломления
или лазерного резонатора со сферическими зеркалами. Такой анализатор позволяет
пространственно разделять цилиндрические моды пучка.
Реализация ДОЭ
для углового спектрального анализа. В [2] вводится понятие моданов - оптических
элементов, используемых в качестве пространственных фильтров для анализа поперечно-модового
состава когерентного лазерного пучка. Аналогичным образом, можно рассматривать
оптические элементы, служащие для разложения светового поля по любому ортогональному
базису как спектральные анализаторы.
На рис.2 показана
оптическая схема для спектрального анализатора светового пучка. Предположим,
что пропускающая функция ДОЭ такого анализатора представляет собой линейную
комбинацию конечного набора базисных функций ?
nm(x,y), выбранных
с заданными наклонами (5). Если такой фильтр поместить рядом со сферической
линзой и осветить световой волной с амплитудой F(x,y),
интенсивность света в точках фокальной плоскости:
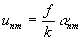 и
и 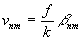 , (29)
, (29)
где (a
nm , b nm)
- несущие пространственные частоты, будут приближенно пропорциональны квадратам
модулей коэффициентов Cnm разложения комплексной амплитуды:
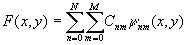 . (30)
. (30)
Действительно,
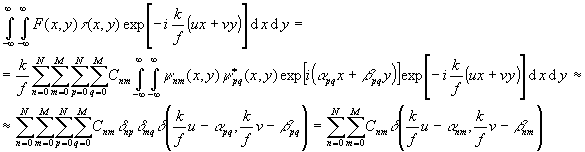 (31)
(31)
В ур-и (31) приближенное
равенство возникает, если пренебречь значениями быстроосциллирующих интегралов
при p¹ n, q¹ m:
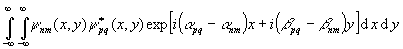 . (32)
. (32)
Чем более эффективно
выполняется разделение пучков, распространяющихся под различными углами, тем
более точно будет выполняться приближенное равенство (31).
Для повышения энергетической
эффективности пространственного фильтра (5) желательно, чтобы он был чисто фазовым.
Задача расчета фазовых ДОЭ, выполняющих разложение светового поля в различных
дифракционных порядках для мод Гаусса-Эрмита и Гаусса-Лагерра без угловых гармоник
рассматривалась в [2,3]. Для пропускающей функции обобщенного фазового анализатора
ур. (5) можно модифицировать следующим
образом:
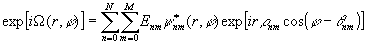 , (33)
, (33)
где (r nm,q
nm) - вектора несущих пространственных частот в полярных координатах,
Enm - комплексные
коэффициенты, модули которых задаются произвольно, а аргументы являются свободными
параметрами задачи, и которые подбираются так, чтобы ур.
(33) было точным равенством.
Для эффективного
пространственного разделения отдельных дифракционных порядков в Фурье-плоскости
предлагается рассматривать следующие
функции
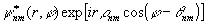 (34)
(34)
приближенно ортогональными
и вычислять коэффициенты в ур. (33) по формуле
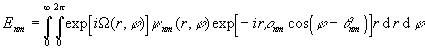 . (35)
. (35)
Предлагаемый итеративный
алгоритм расчета фазовой функции фильтра W
(r,j ) основан на последовательном
вычислении сумм (33) и интегралов (35) с помощью алгоритма быстрого преобразования
Фурье, с учетом определенных ограничений. Например, на
p-ой итерации коэффициенты
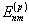 находятся из ур. (35) и заменяются на
находятся из ур. (35) и заменяются на 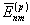 следующим образом
следующим образом
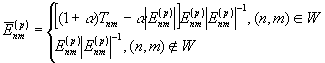 , (36)
, (36)
где Tnm>0
заданные числа, характеризующие отклик каждого канала разложения, W -
множество пар индексов с ненулевыми значениями Tnm,
и 0<a ? 2 - адаптивный или релаксационный коэффициент, позволяющий
контролировать сходимость алгоритма.
Следующая, (p+1)-ая,
оценка фазовой функции фильтра находится
из уравнения
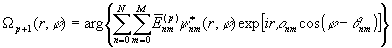 . (37)
. (37)
Далее функцию W
p+1(r,j ) подставляют в ур. (37) и на следующей итерации
находят коэффициенты 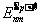 ,
и так далее. Можно доказать релаксационное свойство ошибки такого итеративного
процесса:
,
и так далее. Можно доказать релаксационное свойство ошибки такого итеративного
процесса:
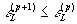 , (38)
, (38)
где 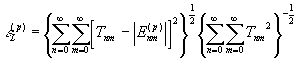 . (39)
. (39)
При численном моделировании
для мод Гаусса-Лагерра использовались
следующие параметры: 128 пикселов по радиусу r и 128 пикселов по угловой
составляющей j , диапазон изменения аргументов rÎ [0,7мм],
j Î [0,2p ],
длина волны l =0.63 мкм, фокусное расстояние f=100 мм, радиус гауссового
пучка в перетяжке a=1 мм. В
формуле (26) рассматривались члены ряда с номерами n,m £
N=7. Действие рассчитанных
ДОЭ моделировалось с помощью
численного преобразования Фурье.
На рис. 5 представлено
формирование 9-ти мод Гаусса-Лагерра ((0,0), (1,0), (1,1), (2,0), (2,1), (2,2),
(3,0), (3,1), (3,2)) в различных дифракционных порядках: фаза ДОЭ (а), сформированные
порядки: интенсивность (б) и фаза (д), эталонное распределение: интенсивность
(в) и фаза (е) и схема, показывающая расположение номеров мод по порядкам (г).
Рассчитанные ДОЭ
могут использоваться не только для формирования пучков Гаусса-Лагерра с заданным
модовым составом, но и как пространственные фильтры для определения поперечно-модового
состава исследуемого пучка. На рис. 6 показано действие ДОЭ, согласованного
с модой Гаусса-Лагерра (5,3), в качестве фильтра (рис. 6б). Из рисунка
видно, что при прохождении моды (5,3) (рис. 6а) через Фурье-каскад, на входе
которого установлен соответствующий фильтр, в центре фокальной плоскости формируется
резкий “всплеск” интенсивности. Если же фильтр согласованный с модой Гаусса-Лагерра
(5,3) осветить другим пучком, например, модой (1,0) (рис. 6г), то в фокальной
плоскости сформируется пятно с четким “провалом” интенсивности в центре (рис.
6д).



а б в



г д е
Рис.5. Многомодовый
пучок в различных дифракционных порядках: фаза ДОЭ (а); номера сформированных
мод (г); распределения интенсивности в фокальной плоскости: полученное при использовании
ДОЭ (б) и эталонное (в); распределения фазы в фокальной плоскости: полученное
при использовании ДОЭ (д) и эталонное (е).



а в


г д
Рис. 6. Действие
одномодового фильтра: интенсивность на входе Фурье-каскада, соответствующая
модам Гаусса-Лагерра (5,3) (а) и (1,0) (г); фаза фильтра, согласованного с модой
(5,3) (б); интенсивность на выходе Фурье-каскада для моды (5,3) (в) и моды (1,0)
(д).
Аналогичное действие,
но для 9-ти модового фильтра, представлено на рис. 7. Пучки, состоящие из одной
моды (2,1) (рис. 7а) и двух мод (2,2)+(3,1) (рис. 7б,в), соответственно,
проходят через фильтр, показанный на рис.5а (соответствие порядков модам см.
на рис. 5г) и производят “всплески” интенсивности в соответствующих точках фокальной
плоскости (рис. 7г и 7д,е) и пятна с “провалами” интенсивности в центрах других
порядков. Пучки, представленный на рис. 7б и 7в отличаются поворотом
на 90 градусов. Результаты, приведенные на рис. 7д и 7е, подтверждают инвариантность
к повороту обобщенных анализаторов с угловыми гармониками.



а б в



г д е
Рис. 7. Действие
многомодового фильтра: интенсивность на входе Фурье-каскада, соответствующая
пучкам Гаусса-Лагерра с модами (2,1) (а) и (2,2)+(3,1) (б,в); интенсивность
на выходе Фурье-каскада для пучка с модами (2,1) (г) и (2,2)+(3,1) (д,е).
3. ДОЭ для разложения
поля по базису Цернике.
Восстановление
фазы светового поля - одна из основных задач обработки сигналов. Не имея возможности
прямым способом измерять фазу светового поля нужно определять ее косвенно, через
измерения интенсивности света. Например, волновой фронт светового поля может
быть восстановлен по интерферограмме, по измерениям распределения интенсивности
пространственного спектра. Датчик волнового фронта Гартмана-Шаке, состоящий
из массива одинаковых узких отверстий или матрицы микролинз, также служит для
восстановления фазы. Восстановить фазу также можно с использованием амплитудно-фазовых
фильтров, раскладывающих световое поле по ортогональному базису [2,3].
В данном разделе
с помощью фазового пространственного фильтра анализируются аберрации волнового
фронта, с использованием разложения поля по базису ортогональных круговых полиномов
Цернике [14]. При этом рассматривается разложение по полиномам Цернике комплексной
амплитуды, а не сами фазовые поля. В этом случае интенсивность, пропорциональная
коэффициентам разложения поля, будет формироваться в пространственной плоскости
Фурье-спектра. Далее, измеренные модули коэффициентов используются для вычисления
аргумента комплексной амплитуды светового поля. Также рассматриваются итеративные
алгоритмы расчета фазы фильтра Цернике и вычисления фазы комплексной амплитуды
светового поля.
Существует полное
множество ортогональных функций с угловыми гармониками в круге радиуса r0.
Это круговые полиномы Цернике [14]:
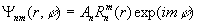 , (40)
, (40)
где  , (41)
, (41)
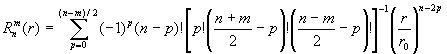 ,
(42)
,
(42)
 -
радиальные полиномы Цернике:
-
радиальные полиномы Цернике:
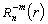 =
= ,
,
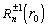 =1,
=1,  ,
,
(r,? )
- полярные координаты.
Разложение светового
поля с комплексной амплитудой E(r,? ) в ряд по функциям (40) записывается
в виде
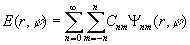 ,
(43)
,
(43)
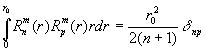 ,
(44)
,
(44)
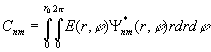 .
(45)
.
(45)
В плоскости пространственного
Фурье-спектра, который может быть сформирован с помощью сферической линзы с
фокусным расстоянием f, комплексная амплитуда светового поля F(?
,? ) будет иметь вид
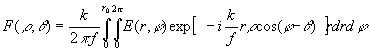 . (46)
. (46)
Основываясь на ур.
(43), можно представить разложение светового поля (46) по полиномам Цернике
из ур. (40) в виде:
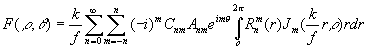 . (47)
. (47)
Интеграл из ур.
(47) берется в явном виде [14]:
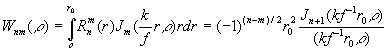 .
(48)
.
(48)
Из ур. (48) видно,
что при n>0 комплексная амплитуда в центральных точках ? =0
равна нулю:
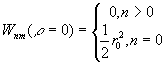 . (49)
. (49)
Следовательно, при
n>0 распределение интенсивности в дифракционных порядках Фурье-плоскости
будет иметь кольцевую структуру.
Так как аберрации
волнового фронта, встречающиеся в оптических системах описываются четными функциями
по отношению к азимутальному углу ? [16], мы можем представить волновое
поле в виде
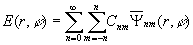 ,
(50)
,
(50)
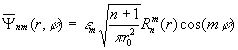 ,
(51)
,
(51)
где 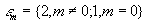 .
.
Заметим, что так
как  , базис
полиномов Цернике содержит единицу в качестве члена разложения. Это означает,
что если осветить фильтр Цернике плоской волной с амплитудой E(r,? )=const,
окажется, что только один коэффициент разложения (43) будет ненулевым:
, базис
полиномов Цернике содержит единицу в качестве члена разложения. Это означает,
что если осветить фильтр Цернике плоской волной с амплитудой E(r,? )=const,
окажется, что только один коэффициент разложения (43) будет ненулевым:
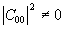 .
.
Из ур. (48) также
следует, что дифракционные порядки, соответствующие базисным функциям с различными
номерами m, но одинаковыми номерами n, будут иметь похожие дифракционные
картины (кольцевые структуры при n > 0 ) в Фурье-плоскости:
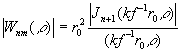 . (52)
. (52)
Параметры моделирования
были выбраны следующие: 256 пикселов по радиусу r и 256 пикселов по углу
j , ro =1
мм, k = 104 мм-1, f = 100 мм. Был рассчитан
25-канальный фильтр, формирующий дифракционные порядки для базисных функций
с номерами (n,m): m?
8 и n? 8, распространяющиеся под некоторыми углами к оптической
оси. На рис.9 показаны: (a)
полутоновая фаза фильтра Цернике (черный цвет соответствует значению фазы 0,
а белый - 2? ), (б) 25 дифракционных порядков, сформированных в частотной
плоскости линзы (негатив), (в) соответствие номеров (n,m)
дифракционным порядкам.


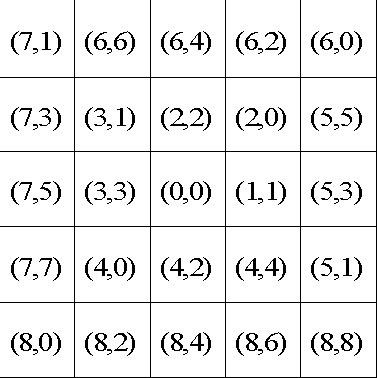
а б в
Рис. 9. Полутоновая
фаза фильтра Цернике (a), распределение интенсивности в частотной плоскости
линзы (б), соответствие номеров (n,m) дифракционным порядкам (в).
Предполагается,
что фильтр освещался плоской волной. В этом случае, анализатор “расщепляет”
падающий плоский пучок на 25 пучков, имеющих примерно одинаковые энергии. На
эти дифракционные порядки приходится более 80% всей энергии освещающего пучка.
Из рис. 9б видно, что интенсивность в центральных точках всех порядков
Фурье-плоскости, кроме нулевого порядка (0,0), нулевая. Это означает, что освещающий
волновой фронт не имеет аберраций.
На рис. 10 представлен
результат действия того же самого 25-канального фильтра Цернике, освещенного
пучком, состоящим из трех базисных функций Цернике с одинаковыми весами и номерами
(n,m): (2,0)+(5,3)+(7,7).
На рис. 10 показаны: (a) интенсивность
освещающего пучка, (б) дифракционная картина в Фурье-плоскости.


а б
Рис. 10. Действие
фильтра Цернике (рис. 9а): интенсивность освещающего пучка (a), дифракционная
картина в Фурье-плоскости (б).
Сравнивая со схемой
распределения номеров мод по порядкам (рис.9в) из рис. 10б видно, что
интенсивность ненулевая (черные точки на рис. 10б) в центральных точках
дифракционных порядков с номерами (2,0), (5,3), и (7,7).
Для распознавания
изображений, когда достаточно измерения модулей коэффициентов разложения,
можно использовать чисто фазовый фильтр (ошибка в измерении модулей коэффициентов
разложения в наших экспериментах была менее 9%). При восстановлении полной
информации о световом поле требуется знать также фазы коэффициентов разложения.
В этом случае следует использовать амплитудно-фазовый фильтр.
Благодарность
Работа выполнена
при содействии Российского фонда фундаментальных исследований (гранты 96-15-96026,
98-01-00894, 99-01-39012).
ЛИТЕРАТУРА
[1] Гончарский А.В.,
Попов В.В., Степанов В.В. "Введение в компьютерную оптику", М., Издательство
МГУ, 1991.
[2] Soifer V.A.,Golub
M.A. Laser beam mode selection by computer generated holograms, CRC Press, Boca
Raton, 1994.
[3] Soifer V.A.,
Kotlyar V.V., Doskolovich L.L. "Iterative methods for diffractive optical elements
computation", Taylor & Francis, London, 1997.
[4] Greisuch G.I.,Bobrov
S.T.,Stepanov S.A. "Optics of diffractive and gradient-index elements and systems",
SPIE Opt. Eng. Press, Washington, 1997.
[5] "Difractive
optics for indastrial and commercial applications" . Edid by F.Wyrowski, and
J.Turunen, Pubishing House Academie Verlag, Berlin, 1997,
[6] Soifer V.A.,
Kotlyar V.V., Khonina S.N., Skidanov R.V., Identification of fingerprints using
the directions fields, Proceedings of the 4-th Russian-German Workshop "Pattern
Recognition and Image Analysis", 139-143, Valday, (1996).
[7] Ярославский
Л.П. Введение в цифровую обработку изображений.- М.:Сов. радио,(1979).
[8] Gerchberg R.W.,
Saxton W.O., A practical algorithm for the determination of phase from im-age
and diffraction plane pictures, Optik, 35, 237-246, (1972).
[9] Берёзный А.Е.,
Прохоров А.М., Сисакян И.Н., Сойфер В.А. Бессель-оптика, ДАН СССР, 234 (4),
802-805 (1984).
[10] Kotlyar V.
V., Khonina S. N., Soifer V. A., Algorithm for the generation of nondiffracting
Bessel modes. J. Mod. Opt., 42 (6), 1231-1239 (1995).
[11] Kotlyar V.
V., Khonina S. N., Soifer V. A., Calculation of phase formers of non-diffracting
images and a set of concentric rings. Optik, 102 (2), 45-50 (1996).
[12] Kotlyar V.
V., Soifer V. A., Khonina S. N. An algorithm for the generation of laser beams
with longitudinal periodicity: rotating images. J. Mod. Opt., 44 (7), 1403-1416
(1997).
[13] Schechner Y.
Y., Piestun R., Shamir J. Wave propagation with rotating intensity distribution.
Physical Rev. E, 54 (1), 51-53 (1996).
[14] Born M., Wolf
E., Principlies of Optics, Pergamon Press, Oxford, (1968).
[15] Artzner G.,
Microlens arrays for Shack-Hartmann wavefront sensors, Opt. Eng. 31(6),
1311-1322 (1992).

