Анализ прохождения электромагнитного импульса через алмазную антиотражающую структуру

Д.Л. Головашкин, В.С. Павельев

Введение

Синтез высокоэффективной оптики для мощных лазеров ИК-диапазона является актуальной проблемой [1,2]. Достижения в области газофазного синтеза позволяют получать поликристаллические алмазные пленки (АП) с оптическими и теплофизическими свойствами, близкими к монокристаллам алмаза (теплопроводность ? 18-20 Вт/см? К [3] и коэффициент поглощения ? 5? 10^-2 см^-1, показатель преломления n=2,38-2,42 для ? =10,6 мкм). Значительный интерес к использованию подобных алмазных пластин толщиной до 1-2 мм и площадью до 100 см² в качестве выходных окон для СО₂ лазеров мощностью 10-20 кВт [4] обусловлен их более высокими порогами тепловой стабильности и разрушения, чем у традиционных материалов ИК оптики (ZnSe, KCl и др.). Однако, задача создания более сложных оптических устройств оставалась нерешенной по двум основным причинам. Во-первых, механическая обработка АП с целью получения требуемого профиля затруднена из-за высокой твердости алмаза. Во-вторых, относительно малая толщина алмазных пластин не позволяет получать традиционным способом оптические элементы с достаточной апертурой. В качестве альтернативы, в работах [5] предлагается использовать АП в качестве подложек дифракционных оптических элементов [6], фазовый рельеф которых формируется методом селективного лазерного травления, разработанного в Институте общей физики РАН. Другой проблемой являются относительно высокие потери энергии, связанные с френелевским отражением, что существенно при фокусировке излучения мощных технологических CO₂-лазеров.Относительно высокий показатель преломления алмаза приводит к тому, что из-за потерь на отражение пропускание алмазной пластины на длине волны 10,6 мкм не превышает 71%. Поэтому особую актуальность приобретает задача просветления АП. Обычные пленочные антиотражающие покрытия значительно уступают алмазу по своим свойствам, что не позволяет использовать в полной мере уникальные свойства АП. В работах [7,8] на результатах натурного эксперимента продемонстрирована эффективность антиотражающих субволновых периодических микроструктур на поверхности алмазной пленки, созданных также методом селективного лазерного травления. Численный анализ работы антиотражающих структур в [7,8] проводился с помощью теории эффективных сред [9]. В рамках этой теории субволновая дифракционная структура рассматривается как градиентная среда с плавно меняющимся поперечным градиентным распределением показателя преломления (Рисунок 1). Однако, приближение теории эффективных сред не учитывает реальных электромагнитных эффектов. В данной работе предлагается метод, позволяющий моделировать прохождение лазерного излучения через антиотражающую структуру в рамках строгой электромагнитной теории света.

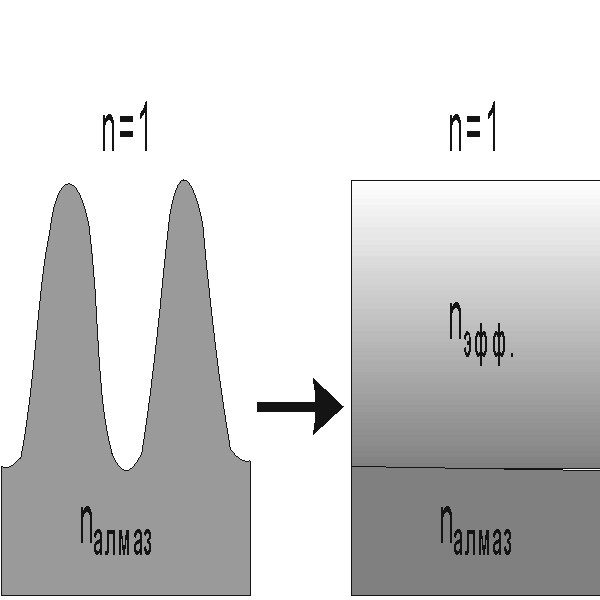
Рисунок 1. Эквивалентная среда для рельефных субволновых решеток на поверхности алмазной пленки

 

 

Построение разностных схем для решения уравнений Максвелла

В работе [10] представлена разностная схема для трехмерного уравнения Максвелла, записанного в системе СИ в декартовой системе координат. Так как дифракционный рельеф наносится в виде полос, то выбор декартовой системы координат с осью X, направленной параллельно полосам, позволяет построить следующие двумерные схемы для волны типа H [11]:

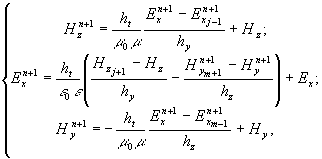(1)

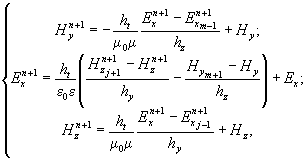(2)

где H_y ,H_z ,E_x – соответствующие проекции векторов напряженности электрического и магнитного полей в декартовой системе координат, ? ₀,? ,? _0,? - диэлектрические и магнитные проницаемости вакуума и среды, h_t, h_y, h_z – шаги дискретизации на сетке ? _ht,hy,hz=? (y_j,z_m,t_n)? D? в области D=? 0? y? L_y, 0? z? L_z, 0? t? L_t? , где j,m,n узлы сетки, причем 0<j<N_y-2, 0<k<N_z-2, 0<n<N_t-2. Для простоты записи у значений полей отображены индексы, отличные от j,k,m. Краевые условия для E_x и H_y первого рода, для H_z второго рода. Считается, что излучение распространяется вдоль оси Z. Полученная схема аппроксимирует краевую задачу с погрешностью аппроксимации O(h_t, h_y, h_z).

Система разностных уравнений (1) решается следующим образом: третье уравнение системы подставляется во второе и получившееся уравнение приводится к трехдиагональному виду:

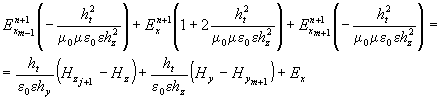(3) ,

которое решается стандартной трехдиагональной прогонкой. Найдя проекцию E_x, подставим ее в первое и третье уравнение системы (1) и найдем H_y и H_z.

Аналогично решается система (2), где трехдиагональное уравнение будет иметь вид:

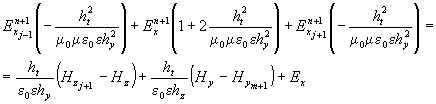(4).

Из уравнений (3) и (4) видно, что когда число отсчетов вдоль области вычислительного эксперимента значительно превышает число отсчетов поперек области, то предпочтительна схема (2), так как в этом случае можно обойтись меньшей оперативной памятью компьютера. Иначе предпочтительна схема (1).

Сравнение результатов численного эксперимента.

Численные эксперименты, результаты которых приведены в Таблице 1, состояли в формировании волн типа H₀₁ (? =10.6 мкм., с цугом в одну длину волны), падающих на границу раздела пластинка-воздух и моделировании дальнейшего распространения прошедших и отраженных волн. Диэлектрическая проницаемость пластинки ? =5.76 Ф/м. Параметры схемы (1) выбирались следующими : L_y=500 мкм., L_z=180 мкм., L_t=8,1? 10^-14 с., h_y=1/3 мкм., h_z=0,2 мкм., h_t=3,5 ? 10^-18 с. Энергия электромагнитного поля определялась как [2] .

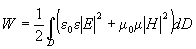Номер численного эксперимента	Форма антиотражающего покрытия	доля отраженной энергии (%)
1	без антиотражающего покрытия	19,24
2	Треугольник с базисом 4 мкм. и высотой 2,5 мкм.	19,24
3	Треугольник с базисом 3 мкм. и высотой 2,4 мкм.	9,8
4	Треугольник с базисом 3 мкм. и высотой 3 мкм.	9,8
5	Треугольник с базисом 3 мкм. и высотой 2 мкм.	11,44
6	Треугольник с базисом 3 мкм. и высотой 1,8 мкм.	12,39
7	Треугольник с базисом 2 мкм. и высотой 2,5 мкм.	9,37
8	Треугольник с базисом 1,5 мкм. и высотой 2,5 мкм.	5,41

Таблица 1. Проявление антиотражающего эффекта при различных формах антиотражающего покрытия

По результатам экспериментов 3-6 можно предположить наличие оптимальной высоты равнобедренного треугольника, являющегося периодом антиотражающей структуры. Структура с треугольниками, у которых высота меньшей оптимальной, обладает меньшим антиотражающим эффектом (сравним эксперимент 3 с экспериментами 5 и 6). А при высоте треугольника больше оптимальной, антиотражающий эффект не увеличивается (сравним эксперимент 3 с экспериментом 4).

На рисунках 2,3,4 представлено разделение падающей волны (эксперименты 1,3,8) на прошедшую через границу раздела алмазная пластинка - воздух и отраженную от этой границы.

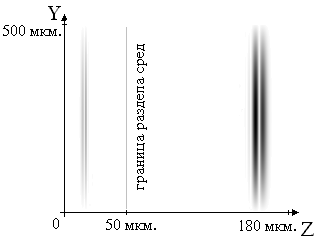
Рисунок 2. Распределение модуля амплитуды электрической составляющей электромагнитного поля в прошедшей и отраженной волне в первом эксперименте

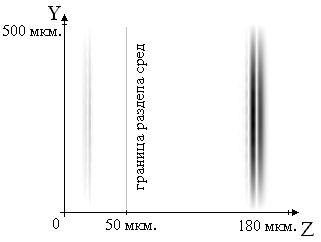
Рисунок 3. Распределение модуля амплитуды электрической составляющей электромагнитного поля в прошедшей и отраженной волне в третьем эксперименте

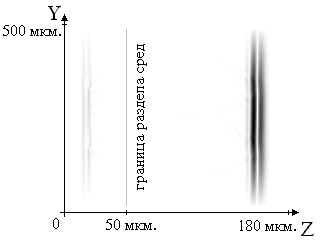
Рисунок 4. Распределение модуля амплитуды электрической составляющей электромагнитного поля в прошедшей и отраженной волне в восьмом эксперименте

На антиотражающий эффект также влияет размер базиса треугольника. С его уменьшением увеличивается доля прошедшей через треугольник энергии (сравним эксперименты 2, 3, 7, 8 и рисунки 2,3,4). Заметно уменьшение доли отраженной энергии на рисунках 3 и 2 по сравнению с рисунком 1.

Рисунки 5,6,7 представляют модовый состав электромагнитной волны по разные стороны от границы раздела сред. Модовый состав лучше отслеживается на продольной проекции магнитной составляющей поля. Это происходит из-за того, что моды низких порядков переносят подавляющую часть энергии волны, а продольная проекция магнитной составляющей поля вносит малый вклад в общую энергию и в ней моды низких порядков незначительно превальируют над остальными модами.

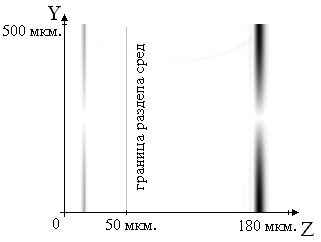
Рисунок 5. Распределение модуля амплитуды проекции Н_z электромагнитного поля в прошедшей и отраженной волне в первом эксперименте

Рисунок 6. Распределение модуля амплитуды проекции Н_z электромагнитного поля в прошедшей и отраженной волне в третьем эксперименте

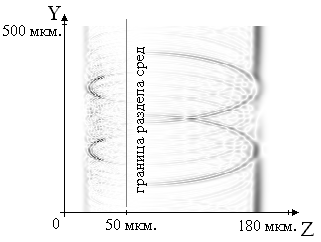
Рисунок 7. Распределение модуля амплитуды проекции Н_z электромагнитного поля в прошедшей и отраженной волне в восьмом эксперименте

Появление мод высших порядков на рисунках 6,7 (в отличии от рисунка 5, где мода низшего порядка) обусловлено непрерывностью электромагнитного поля на антиотражающем рельефе. Каждый фрагмент рельефа, содержащий от одного периода и более, формирует набор мод порядка L_z? a/d , где d- период антиотражающего рельефа, a – число периодов во фрагменте. Подробнее модовая структура представлена на рисунках 8,9.

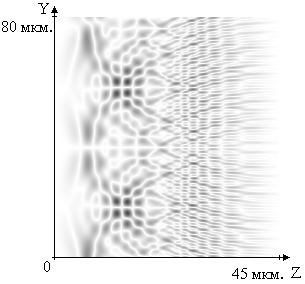
Рисунок 8. Фрагмент распределения модуля амплитуды проекции Н_z электромагнитного поля в отраженной волне в третьем эксперименте

Рисунок 9. Фрагмент распределения модуля амплитуды проекции Н_z электромагнитного поля в прошедшей волне в третьем эксперименте

Заключение

В данной работе показана возможность использования разностного решения уравнений Максвелла для анализа работы антиотражающих алмазных субволновых структур. Результаты проведенного численного моделирования находятся в хорошем согласовании с результатами натурных исследований, опубликованных в [7,8], и результатами численного анализа с помощью теории эффективных сред второго порядка [9]. Таким образом, разностное решение уравнение Максвелла впервые позволило провести моделирование алмазных антиотражающих структур и оценить их эффективность в рамках теории электромагнитного поля, а также провести анализ тонкой структуры отраженной электромагнитной волны.

Список литературы

1. Golub M.A., Sisakyan I.N., Soifer V.A. Infra-red radiation focusators// Optics and Lasers in Engineering.- 1991.-Vol. 15.- P. 297-309.
2. Duparre' M., Golub M.A., Ludge B.,Pavelyev V.S., Soifer V.A., Uspleniev G.V., Volotovskii S.G. Investigation of computer-generated diffractive beam shapers for flattening of single-modal CO₂-laser beams// Applied Optics. - 1995. - Vol.34, N 14.- P. 2489-2497.
3. V. Ralchenko, A. Vlasov, I. Vlasov, B. Zubov, A. Nikitin, A. Khomich, SPIE Proc. 3484, Int. Conf., Tashkent, Uzbekistan, 1998
4. Sussmann R.S., Brandon J.R., Coe S.E., Pickles C.S.J., Sweeney C.G., Wasenczuk A., Wort C.J.H., Dodge C.N., Finer Points, 10(2), 6, (1998).
5. В.В. Кононенко, В.И. Конов, С.М. Пименов, А.М. Прохоров, В.С. Павельев, В.А. Сойфер, Квантовая электроника, 26(1), 9-10, (1999)
6. Сойфер В.А., Введение в дифракционную микрооптику, (Самара, 1996).
7. Kononenko T.V., Kononenko V.V., Konov V.I., Pimenov S.M., Garnov S.V., Tischenko A.V., Prokhorov A.M., Khomich A.V., Applied Physics A, 68(1), 99-102, (1999).
8. В.В. Кононенко, Т.В. Кононенко, В.И. Конов, С.М. Пименов, С.В. Гарнов, А.В. Тищенко, А.М. Прохоров, А.В. Хомич, Квантовая электроника, 26(2), 158-162, (1999)
9. Daniel H. Raguin, G. Michael Morris Antireflection on structured surfaces for the infrared spectral region, Applied Optics, Vol. 32, N. 7, p.p. 1154-1167 (1993)
10. Головашкин Д.Л., Разностная схема для уравнений Максвелла, Труды девятой межвузовской конференции, Самара, 1999, стр. 43-45.
11. Никольский В.В., Никольская Т.И., Электродинамика и распространение радиоволн, М.:Наука,1989.-544с.