ИНВАРИАНТНЫЕ МНОГОМОДОВЫЕ ПУЧКИ.

С.Н. Хонина, В.А. Сойфер

Институт систем обработки изображений Российской Академии Наук

443001 г. Самара, ул. Молодогвардейская, 151

e-mail: ipsi@smr.ru

 

Введение.

Инвариантность (неизменяемость) – основное свойство мод лазерного излучения при распространении в своей среде. То есть, в процессе моды не изменяют своей пространственной структуры, приобретая лишь фазовый набег.

Бесселевы моды, например, распространяются не изменяясь внутри сердцевины круглого оптического волокна со ступенчатым показателем преломления [1], а также в свободном пространстве. Для оптического волокна с параболическим показателем преломления характерны моды Гаусса-Лагерра или Гаусса-Эрмита [2], в зависимости от того, круглое или квадратное сечение волокна. С точностью до масштаба гауссовы моды сохраняют свою структуру и в свободном пространстве.

Инвариантные свойства мод можно использовать для передачи информации. Например, чтобы передать на расстояние некоторое изображение по оптическому волокну, оно должно обладать инвариантными в данной среде свойствами. Под инвариантным изображением будем понимать поперечное распределение интенсивности светового пучка, которое сохраняется с точностью до масштаба и поворота (в обоих случаях изображение узнаваемо) при распространении в некоторой среде. Сформировать такие изображения можно с помощью композиции соответствующих мод [3,4].

Понятно, что не любая композиция мод будет обладать инвариантными свойствами. В данной работе рассматриваются многомодовые световые пучки Бесселя и Гаусса-Лагерра и выясняются условия их инвариантности. Так как свойство инвариантности тесно связано с эффектом самовоспроизведения [5,6], то рассматриваются не только стабильные и вращающиеся, но и периодически повторяющиеся пучки.

Для формирования инвариантных многомодовых пучков предлагается использовать дифракционные оптические элементы (ДОЭ), рассчитанные с помощью методов компьютерной оптики [7,8]. В данной работе приводятся результаты численного моделирования работы таких ДОЭ.

1. Бесселевы моды.

В общем случае многомодовый Бесселевый пучок лазерного света может быть описан как линейная комбинация частных решений уравнения Гельмгольца. Эти частные решения являются произведением функций Бесселя первого рода на угловую гармонику. Итак, для комплексной амплитуды такого светового пучка на некотором расстоянии z от начальной плоскости (z=0) можно записать [9]:

, (1)

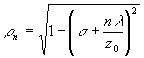, (2)

 

где k=2p /l - волновое число света с длиной волны l , (r,? ) - полярные координаты, J_m(x) - функция Бесселя первого рода m-го порядка, z₀ - период саморепродукции поля, s =cos? ₀, ? ₀ - начальный угол наклон плоских волн пространственного спектра светового поля.

Требование положительности подкоренного выражения в уравнении (2) накладывает ограничения на возможный выбор чисел n:

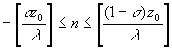, (3)

где ? ...? обозначает целую часть числа. Заметим, что при n больших, чем задает неравенство (3), вместо функций Бесселя первого рода J_m(x) в ур. (1) появятся функции Бесселя второго рода (модернизированные) I_m(x), которые также имеют физический смысл [10].

Как видно из ур. (2) плоские волны, составляющие пучок (1) имеют волновые вектора, которые лежат на конических поверхностях с образующими, наклонными к оси z под углами ? _n, удовлетворяющими соотношению:

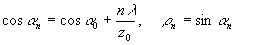. (4)

Концы этих волновых векторов, лежащих на конусах, описывают окружности разных радиусов, что соответствует теории Монтгомери для самовоспроизводящихся световых полей [5].

Из уравнения (1) следует, что если отличные от нуля коэффициенты C_mn имеют одинаковый номер n=n₀, то световое поле распространяется инвариантно, без изменения вида как Бесселева мода:

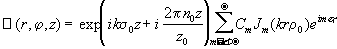, (5)

где .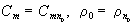

Продольная периодичность светового поля (1) имеет место, когда хотя бы два слагаемых с различными номерами n и n? отличны от нуля.

Вращение поперечного сечения светового пучка, описываемого выражением (1), является частным случаем продольной периодичности и обеспечивается согласованным выбором отличных от нуля слагаемых с разными номерами n и m . Для получения условия вращения пучка вместо уравнения (1) запишем выражение для интенсивности:

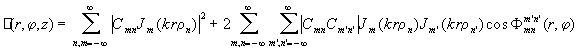, (6)

. (7)

Из выражения (7) следует, что вид функции не изменится при условии

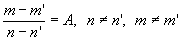, (8)

где A - постоянная величина. Из (8) следует, что если в уравнении (1) отличны от нуля только два слагаемых, то при любых значениях их номеров 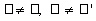световое поле будет вращаться вокруг оси распространения. Из (8) также следуют менее общие, но более удобные для использования условия вращения пучка:

, (9)

. (10)

При выполнении условия (8), (9) или (10) с изменением расстояния на величину ? z значение интенсивности I(r, j , z) в уравнении (6) не изменится при выборе величины угла j +? j , где

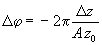. (11)

Из уравнения (11) видно, что если A^-1 - целое число, то на длине периода z₀ будет совершаться целое число оборотов при вращении пучка. При этом направление вращения (левое или правое) определяется знаком постоянной A.

Алгоритм расчета фазовых ДОЭ, формирующих световые пучки с амплитудой (1) предложен в [9]. На первой итерации этого алгоритма фаза ДОЭ S₀(r,? ) выбирается как аргумент суммы (1) при z=0, и далее используются следующие формулы:

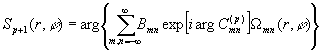, (12)

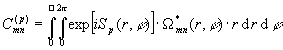, (13)

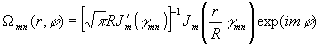, (14)

где B_mn - неотрицательные числа, которые задаются произвольно и определяют вид поперечного распределения интенсивности светового поля, 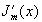- производная функции Бесселя, kRr _n = ? _mn, g_m,n - корни функции Бесселя: J_m(g_mn) = 0, g_-m,n = g_m,-n = g_-m,-n = g_m,n .

2. Моды Гаусса-Лагерра

В многомодовом световом волокне круглого сечения и с квадратичной зависимостью показателя преломления

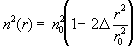, (15)

где n₀ - максимальное значение показателя преломления на оси волокна, r₀ - радиус волокна, ? - параметр дисперсии показателя преломления, распространяется световое поле, являющееся суперпозицией мод Гаусса-Лагерра [10]:

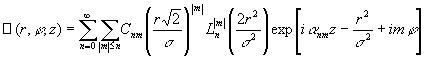, (16)

где 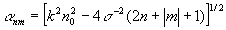- коэффициент, пропорциональный фазовой скорости соответствующей моды, 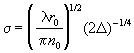- эффективный радиус первой моды, 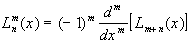- обобщенный многочлен Лагерра.

Чтобы в оптическом волокне распространялся инвариантный многомодовый пучок Гаусса-Лагерра необходимо соблюсти условие равенства фазовых скоростей

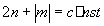. (17)

В противном случае из-за дисперсии фазовых скоростей мод Гаусса-Лагерра сформированное на входе волокна изображение U(r,? , z=0) будет деградировать по мере распространения. Чтобы частично компенсировать дисперсию фазовых скоростей мод нужно из суммы (16) выбрать такие слагаемые, для которых фазовые скорости некоторым образом согласованы. Например, можно заставить световой многомодовый пучок, сгенерированный фазовым ДОЭ вращаться вокруг оси по спирали. Условия вращения поперечного сечения пучка (16) аналогичны условиям (8)-(10) для многомодовых пучков Бесселя и имеют соответственно вид:

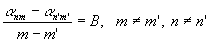, (18)

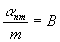, (19)

где B - постоянная величина. В уравнении (18) величины ? _nm можно приближенно заменить на следующее выражение

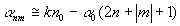, (20)

так как kn_{0 ? ?} ? ₀, 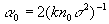. Например, при характерных параметрах волокна: r₀ =10 мкм, ? =0.01, n₀ =1.5, и для видимого света: k=10⁴ мм^-1, получим следующие значения: kn₀ =1.5´ 10⁴ мм^-1 и ? ₀ =15 мм^-1.

С учетом уравнения (20) условие (18) будет иметь более простой вид:

, n, n', m, m' =0,1,2,... (21)

При небольших значениях номеров мод (n? 10) приближенное равенство в уравнении (20) соблюдается при выбранных параметрах волокна с точностью около 2%.

Период z₀, на котором будет происходить полный оборот, рассчитывается по формуле:

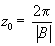(22)

и для выбранных параметров равен десяткам и сотням микрон.

Алгоритм расчета фазовых ДОЭ выглядит аналогично (12)-(14):

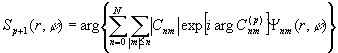, (23)

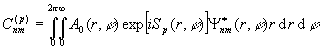, (24)

, (25)

где - известная амплитуда освещающего пучка, модули коэффициентов 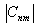задаются произвольно и характеризуют энергетический вклад каждой моды в пучок, а аргументы 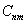являются свободными параметрами задачи.

3. Численное моделирование

Пример инвариантного пучка или стабильной моды Бесселя показан на рис.1 в верхней строке. Параметры расчета следующие: l =1.06 мкм, R=1 мм, s ₀=0.01. На рис.1 в верхней строке показаны: полутоновая фаза ДОЭ (а) (черный цвет - 2p , белый - 0), формирующего световой пучок, эффективно состоящий из четырех слагаемых в уравнении (1) с номерами (m,n): (-3,-1), (-1,-1), (0,-1), (2,-1). Модули коэффициентов выбирались одинаковыми. Так как все слагаемых имеют одинаковый номер n=-1, то согласно уравнению (5) световое поле при распространении не изменяет свою структуру. Это видно из рис. 1, на котором в верхней строке показаны распределения поперечной интенсивности данного пучка (негатив) на расстояниях z: 30 мм (б), 40 мм (в), 50 мм (г), 60 мм (д), 70 мм (е).

Пример светового поля, периодически изменяющегося при распространении, показан в средней строке на рис. 1. Параметры расчета: l =1.06 мкм, z₀=20 мм, R=1 мм, s ₀=0.015. В уравнении (1) сохранялись отличными от нуля четыре слагаемых с номерами (m,n): (-2,1),
(-1,2), (1,2), (2,1). Модули коэффициентов выбирались одинаковыми. При этом условия вращения (8)-(10) не соблюдаются. На рис. 1 в средней строке показаны: полутоновая фаза ДОЭ (а) и поперечные распределения интенсивности, сформированные на расстояниях z: 45 мм (б), 50 мм (в), 55 мм (г), 60 мм (д), 65 мм (е). Видно повторение поперечной структуры пучка через период и искажение внутри периода.

В нижней строке рис. 1 показан пример вращающегося многомодового пучка Бесселя. Параметры расчета: l =1.06 мкм, z₀=10 мм, R=2 мм, s ₀=0.02. В уравнении (1) отличными от нуля выбирались только три слагаемых с номерами (m,n): (-3,-3), (-2,-2), (-1,-1). Соотношение модулей коэффициентов было следующим: |C_-3,-3|=3, |C_-2,-2|=2, |C_-1,-1|=1. Условия вращения (8)-(10) для данных номеров соблюдаются. На рис. 1 в нижней строке показаны: полутоновая фаза ДОЭ (а), формирующего световой пучок, эффективно содержащий три моды Бесселя, поперечные распределения интенсивности которого показаны на расстояниях z: 30 мм (б), 32.5 мм (в), 35 мм (г), 37.5 мм (д), 40 мм (е). Из рисунка видно, что имеет место вращение пучка при его распространении, но также видно, что происходят некоторые изменения вида картины поперечного сечения пучка, обусловленные интерференцией трех главных мод (около 90% энергии) с модами высших порядков.

Поперечные картины дифракции вычислялись с помощью преобразования Френеля, которое, в свою очередь, вычислялось с помощью алгоритма быстрого преобразования Фурье.

 

 

 

а б в г д е

Рис. 1. Численные результаты формирования многомодовых Бесселевых пучков: инвариантного (верхняя строка), периодического (средняя строка) и вращающегося (нижняя строка); итеративно рассчитанные фазы ДОЭ (а) и поперечные сечения сформированных пучков на различных расстояниях (б-е).

На рис. 2 показаны некоторые примеры численного моделирования распространения многомодовых пучков Гаусса-Лагерра в градиентном волокне. Параметры расчета: r₀ =15 мкм, ? =0.01, n₀=1.5, l =0.63 мкм, ? ₀ =15 мм^-1, гауссовый освещающий пучок, модули коэффициентов равны.

На рис. 2 в верхней строке приведен пример инвариантного пучка Гаусса-Лагерра, распространяющегося в волокне почти без изменения. В уравнении (16) отличными от нуля выбирались четыре слагаемых с номерами (n,m): (5,-3), (5,3), (6,-1), (6,1), которые удовлетворяют уравнению равенства фазовых скоростей (17). При этом уравнения (21)-(22) приводят к бесконечному периоду вращения z₀=¥ , B=0. На рис. 2 в верхней строке показаны: бинарная фаза ДОЭ (а) и поперечные сечения сформированного пучка (негатив), рассчитанного на разных расстояниях z: 1 мм (б), 2 мм (в), 3 мм (г), 4 мм (д), 5 мм (е). Видно, что при распространении такого пучка происходит незначительная модуляция интенсивности, обусловленная периодически изменяющимся влиянием высших мод Гаусса-Лагерра. В расчете учитывались всего 50 мод с ближайшими номерами.

Пример периодически изменяющегося многомодового пучка Гаусса-Лагерра показан в средней строке на рис. 2. В этом случае в уравнении (16) отличными от нуля считались слагаемые с номерами (n,m): (4,-3), (4,-1), (4,0), (4,1), (4,3). Условия вращения (18) и (19) не соблюдаются, однако полученные значения B оказались кратными, что позволило выделить общий период z₀=0.6235 мм. На рис. 2 в средней строке показаны бинарная фаза ДОЭ (а) и поперечные сечения светового пучка на разных расстояниях z: 1 мм (б), 1.156 мм (в), 1.312 мм (г), 1.467 мм (д), 1.623 мм (е). Видно, что происходит периодическая смена картин дифракции при распространении пучка в волокне. Через период изображение повторяется.

В нижней строке на рис. 2 приведен пример вращающегося многомодового пучка Гаусса-Лагерра. В сумме (16) сохранялись три слагаемых с номерами (n,m): (4,-2), (4,0), (2,2). Условие вращения (18) выполняется, период вращения z₀=0.6246 мм. На рис. 2 в нижней строке показаны полутоновая фаза ДОЭ (а) и поперечные сечения пучка на разных расстояниях в пределах полуоборота z: 1 мм (б), 1.078 (в), 1.156 мм (г), 1.234 (д), 1.312 мм (е). Распределение интенсивности поперечного сечения пучка вращается как единое целое, сохраняя свою структуру.

Способ выбора номеров для более двух слагаемых в сумме (16), удовлетворяющих условию вращения (21) подробно описан в [4].

 

 

 

а б в г д е

Рис. 2. Численные результаты формирования многомодовых пучков Гаусса-Лагерра: инвариантного (верхняя строка), периодического (средняя строка) и вращающегося (нижняя строка); итеративно рассчитанные фазы ДОЭ (а) и поперечные сечения сформированных пучков на различных расстояниях (б-е).

 

Благодарность

Работа выполнена при содействии Российского фонда фундаментальных исследований (гранты 96-15-96026, 98-01-00894, 99-01-39012).

 

 

Литература

1. Унгер Х.Г., Планарные и волоконные оптические волноводы. М.: Мир, 1980
2. Snyder A.W., Love J.D., Optical waveguide theory. Chapman and Hall, 1984
3. Kotlyar V.V., Khonina S.N., Soifer V.A., Calculation of phase formers of non-diffracting images and a set of concentric rings, Optik, v.102, No.2, p.45-50 (1996)
4. Хонина С.Н., Формирование и передача на расстояние изображений с помощью мод Гаусса-Лагерра, Компьютерная оптика, Самара-Москва, вып. 18, с.71-81, 1998
5. Montgomery W.D., Self-imaging objects of infinite aperture, J. Opt. Soc. Am., 57(6), 772-778 (1967).
6. Бельский А.М., Самовоспроизводящиеся пучки и их связь с недифрагирующими пучка-ми. Оптика и спектроскопия 73(5), 947-951 (1992).
7. Soifer V.A., Golub M.A., Laser beam mode selection by computer-generated holograms. Boca Raton: CRC Press, U.S., 1994.
8. Soifer V.A., Kotlyar V.V., Doskolovich L.L. Iterative methods for diffractive optical elements computation. London: Taylor & Francis, 1997.
9. Kotlyar V.V., Soifer V.A., Khonina S.N. An algorithm for the generation of laser beams with longitudinal periodicity: rotating images. J.Modern Opt. 44(7), 1409-1416 (1997)
10. Ruschin S. Modified Bessel nondiffracting beams. J.Opt.Soc.Am. A 11(12), 3224-3228 (1994)
11. Adams M.J., An introduction to optical waveguides, J.Wiley & Sons, Chichster, 1981.